视线追踪系统中基于黎曼几何的落点补偿方法研究

金　纯，李娅萍

(1. 重庆邮电大学 无线传输重点实验室 重庆 400065；2.重庆金瓯科技发展有限责任公司，重庆 400041)



视线追踪系统中基于黎曼几何的落点补偿方法研究

金纯1,2，李娅萍1

(1. 重庆邮电大学 无线传输重点实验室 重庆 400065；2.重庆金瓯科技发展有限责任公司，重庆 400041)

摘要：针对非接触式视线跟踪系统中注视点估计算法鲁棒性差的问题，对单相机双光源的视线追踪系统进行了改进。在空间相似三角形注视点估计算法的基础上，提出一种基于黎曼几何的视线落点补偿方法。在眼球模型结构的基础上分析了眼球角膜曲面对视线落点偏差的影响。根据人类眼球生理特点，在黎曼几何中对眼球曲面结构进行建模，提出以最短测地线长度为边长构造平面三角形，以补偿欧式几何中直线距离造成的视线落点的误差。利用非线性多项式模型对眼球视轴和光轴之间的偏差进行拟合，得到最终的视线落点。实验证明，该方法在水平和垂直方向上最大误差均小于1 cm，对视线落点补偿具有显著效果。

关键词：视线跟踪；黎曼几何；相似三角形；视轴；光轴

0引言

视线跟踪技术是利用人类眼球运动信息来达到控制设备目的的一种科学应用技术，解决了上肢有残疾或者双手因执行操作任务而被占用的人员对计算机等终端设备操作的难题，近年来迅速获得国内外相关学者的广泛关注。就目前的视线跟踪系统而言，尽管其技术优势明显，但是由于人类眼球生理结构的复杂性和用户自由头动的需求，使得跟踪精度和用户自由度无法满足实际的应用要求[1]。Morinoto等[2]提出一种非接触式的视线跟踪方法，采用瞳孔向量反射方法，通过二阶多项式拟合方程来确定注视点的位置，该系统在头部静止情况下追踪精度可达到1.5°—2°，目前为止，其应用十分广泛。郑思仪等[3]提出一种基于眼球结构的视线映射几何模型设计，通过光源与角膜反射点得到角膜曲率中心和光轴的空间直线，利用光轴和视轴之间的夹角得到视轴的方向，解决了用户头动状态下的视线落点精度计算的问题，该系统在距离屏幕35 cm，头部局限20 cm的大圆内，跟踪精度在水平方向可达1.4°，垂直方向可达1.6°。张鹏翼等[4]使用立体视觉信息的视线追踪系统设计，使用神经网络结合卡尔曼滤波的方法对瞳孔进行跟踪，再结合支持向量回归对人眼参数和注视点之间的关系进行训练，可得到视线映射模型，该系统在相机光轴方向30 cm头动范围内，追踪精度可达到1.8°。

但是上述作者所建立的视线跟踪系统都存在一定的问题，如文献[2]对用户头动十分敏感，头动状态下追踪精度大大下降。文献[3]虽然在用户自由度方面有了提高，但是摄像机和光源等需要保持相对静止，一旦移动则需要重新标定，并且还需要进一步提高三维测量的精度。文献[4]在训练过程中，算法冗余度和精度不能很好地满足系统需要，并且在成熟度和实用性方面有所欠缺。

针对以往视线跟踪系统存在的不足，本文基于单相机双光源的非接触式视线跟踪系统，提出了一种基于黎曼几何的视线落点误差补偿方法。该方法将眼球曲面在黎曼几何中进行建模，提出以黎曼几何中最短测地线的长度构造平面三角形，来补偿欧式几何中直线距离造成的视线落点的误差，通过非线性多项式模型对眼球视轴和光轴之间偏差进行拟合，得到最终的视线落点。该方法解决了眼球的生理结构造成的视线落点误差的问题，将黎曼几何应用到视线跟踪系统中，不仅大大提高了系统的精度，而且开创了利用黎曼几何研究视线跟踪系统的先河[5]。

1视线追踪系统

本文提出一种以瞳孔-角膜反射法为视线追踪方法、注视点估计精度高且对用户无干扰的单摄像机双光源视线跟踪系统，主要由相机、2个近红外光源、图像采集卡及计算机组成。系统采用红外光源照射眼睛，人眼角膜对红外光有较大的反射率，产生反射光斑。当眼睛注视不同方向时，光从不同角度照射到角膜，瞳孔中心随着视线方向发生相应的变化，角膜反射点的位置固定不变。利用眼球和角膜反射点的这种特性，提取视线特征参数，通过相应的注视点估计方法就可以得到视线的落点位置[6]。

在人眼定位阶段，采用基于灰度差的人眼定位方法。利用人脸、角膜反射点和瞳孔之间的灰度差来定位人眼，针对瞳孔以及反射点的形状特点来消除外界干扰因素对人眼定位的影响[7]。定位人眼区域后，根据灰度值、面积、相对位置关系以及瞳孔结构特性，大致定位出瞳孔区域，通过灰度值迭代的方式来精确定位瞳孔区域。在特征参数提取过程中，首先对瞳孔边缘进行检测，然后利用椭圆拟合法和质心法确定瞳孔和光斑中心[8]。最后，采用基于空间相似三角形的双光源注视点估计算法得到视线在屏幕上的落点。

本文的主要内容就是在上述算法的基础上，提出一种基于黎曼几何的视线落点补偿方法。

2视线映射模型及基于弧长的视线落点误差补偿

2.1视线映射模型

基于空间相似三角形的双光源注视点估计算法的原理是依据人眼特性以及人眼视觉成像原理，人眼图像中的瞳孔中心以及2个角膜反射点构成的三角形与计算机屏幕上注视点位置以及2个近红外光源构成的三角形之间可以近似看作一对相似三角形，相对应各边成比例，估计出屏幕上注视点的近似位置[9]。

图1为相似三角形算法原理图。L是计算机平面，L1和L2是放置在计算机屏幕上的2个红外光源，Q是计算机平面上注视点位置。E是眼平面，E1和E2分别是2个红外光源在人眼角膜上形成的反射点，EQ是瞳孔中心。P为相机拍摄人眼图像平面，PQ为人眼图像中瞳孔中心，P1和P2为人眼图像中2个角膜反射点。C是人眼角膜的曲率中心。

Q点坐标位置可按(1)式获得。

(1)

(1)式中：(XQ,YQ)为计算机屏幕上视线落点坐标； (XL1,YL1)，(XL2,YL2)分别为2个红外光源的坐标，XL1，YL1，YL2的值均为0，XL2的值为计算机屏幕宽度，可通过测量获得；(XPQ,YPQ)，(XP1,YP1)，(XP2,YP2)分别为人眼图像中瞳孔中心和2个反射点的坐标，它们的坐标值已通过第1节获得。

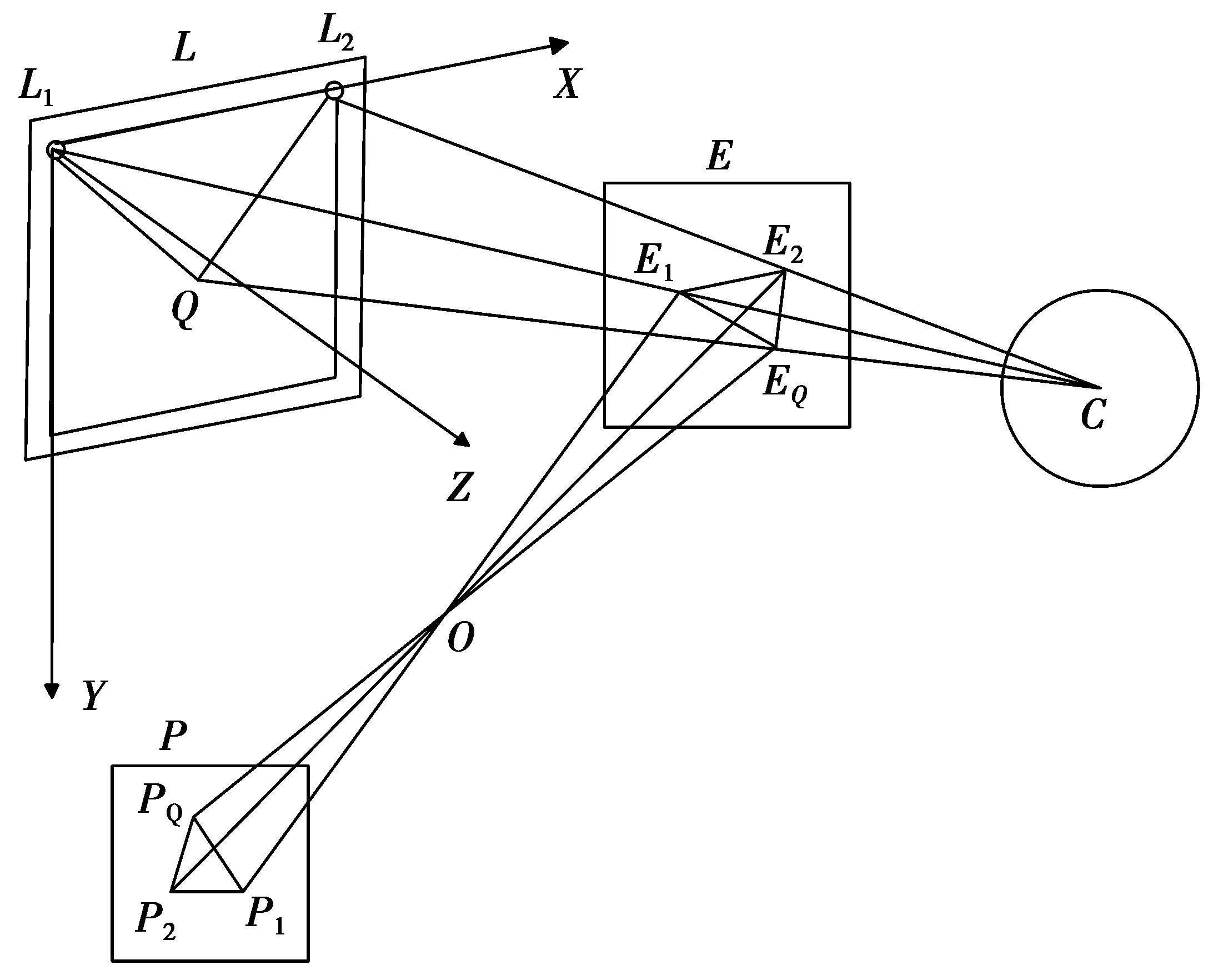
图1　相似三角形算法原理图Fig.1　Principle of similar triangles algorithm

2.2基于黎曼几何的视线落点误差补偿

图2　立体的人眼结构图Fig.2　Human eye diagram

黎曼几何中，光线是按曲线运动的，任意2点之间的最短距离为曲线，即最短测地线。测地线是欧式空间中的直线段在黎曼流形或一般的仿射联络空间中的推广。该系统中，以计算机平面上2个光源之间的距离为例，其在眼球曲面上的映射为2个光斑之间的最短测地线的弧长。也就是说，计算机平面上由视线落点和2个光源组成的三角形与眼球曲面上以对应映射点之间最短测地线的长度为边长的三角形是相似的[11]。图3为基于黎曼几何的视线落点补偿方法原理图。其中，T为把眼球曲面E展开后形成的平面，且与计算机平面平行。T上三角形为以眼球曲面最短测地线弧长为边长的三角形，该三角形与人眼眼球角膜曲面上三角形为同胚的，与计算机屏幕三角形是相似的[12]。

设S1=Π∩Sn是眼球面Sn上任意一个大圆，其中Π是过球心和2个角膜反射点A，B的一个二维平面。存在Sn到其自身的等距φ，使得φ的不动点集恰好是曲线S1上的点构成的集合，那么，S1是Sn上的测地线。由于在任意一点沿任意的一个切方向，都有一个大圆通过该点并且与该方向相切，根据测地线的唯一性，Sn上的测地线只能是大圆或其一部分。若设大圆S1的参数方程为γ(t)，根据定义

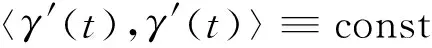
(2)

(2)式中,const为一常量。

图3　基于黎曼几何的视线落点补偿方法原理图Fig.3　Principle of gaze point compensation algorithmbased on Riemannian geometry

假设|γ′(t)|=c，c始终为一固定值，且不同用户曲率值有可能不同，可由测试得到。

则大圆S1上连接A，B 2个点的测地线γ(t)， t∈[t0,t]的弧长为

(3)

求得弧长之后，根据相似三角形对应边成比例的关系得到补偿后视线落点Q1坐标为

(4)

(4)式中：(XQ1,YQ1)为补偿后视线落点坐标；点Q1坐标为人眼光轴映射到计算机屏幕上的落点，而真正的视线落点为视轴到计算机屏幕的映射点，由于光轴和视轴之间的角度变化呈非线性状态，最大角度约为5°的夹角[13]，因此，提出非线性多项式模型对它们之间的关系进行解释[12]。

(5)

3实验结果

本文视线跟踪系统选取多名测试者对视线估计结果进行测试。试验中记录的注视点是以像素为单位的，首先须将屏幕上观察到的像素转换为实际的长度。测试过程中，采用的计算机屏幕分辨率为1 366像素×768像素，经过测量，屏幕的实际尺寸为410mm×230mm。每个像素的长度在水平方向上为410mm/1366pixel，垂直方向为230mm/768pixel。测试者在距离屏幕60—70cm处，头部可自由运动，能适应的运动范围约为20cm×17cm×10cm(水平×垂直×前后)。测试过程中，由于人眼光轴和视轴之间的固有偏差以及注视点估计算法中近似的影响，系统需要一个对每个测试者进行校准的过程，记录下测试者盯视校准点时对应的视线参数，求出多项式非线性映射函数的系数。本文将计算机屏幕分成相等的9个部分，取每个部分的中心点为校准点，对9个点进行校准的结果如图4所示。

图4　用户校准结果Fig.4　Result of the calibration

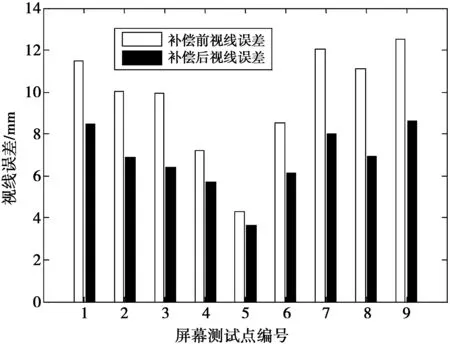
图5　补偿前后视线误差对比Fig.5　Contrast of gaze point error with/without compensation

图6　补偿前后视线估计落点对比Fig.6　Contrast of estimated gaze pointwith/without compensation

由图5和图6可以得到如下结论。

1)基于黎曼几何的视线落点误差补偿方法效果比较明显，补偿前，视线误差较大，视线估计落点与真实值偏离距离比较远，仿真图6中，“×”点分布比较分散，经过补偿后，视线落点与真实值之间误差明显减小，视线落点集中分布在真实值周围，“·”点比较紧密地聚集在一起。

2)补偿前视线落点在X轴上平均误差为10.674 4mm，Y轴上平均误差为11.043 3mm；补偿后视线落点在X轴上平均误差为7.655 6mm，Y轴上平均误差为8.326 5mm。

3)Y轴平均误差高于X轴的平均误差，因为垂直分辨率低于水平分辨率。并且，当测试者靠近摄像机时，视线误差会显著降低，因为随着距离的缩短，眼睛图像的分辨率增大，盯视精度得到提高。

4结论

实验证明，本文提出的基于黎曼几何的视线落点误差补偿方法具有较显著的效果，采用黎曼几何的观点对眼球角膜曲面进行分析，研究黎曼几何和欧式几何的映射关系，并利用最短测地线的弧长来弥补角膜曲面上2点之间欧式距离的误差，使人眼与计算机屏幕之间的映射模型更为精准，最后对眼球视轴和光轴之间偏差进一步补偿。方法具有较高的估计精度，补偿后在水平方向平均精度为0.55°，平均误差为7.655 6 mm；垂直方向上平均精度为0.60°，平均误差为8.326 5 mm。与补偿前系统相比，追踪精度和用户自由度得到较大提升。

参考文献：

[1]TORRICELLI D,CONFORTO S,SCHMID M,et al.A neural-based remote eye gaze tracker under natural head motion[J].Computer Methods Programs Biomed,2008,92(1):66-78.

[2]MORIMOTO C H, KOONS D, AMIT A, et al. Pupil detection and tracking using multiple light sources [J]. Image and Vision Computing, 2000，18(4):331-335.

[3]郑思仪,王志良,张鹏翼.一种基于眼球结构的视线映射几何模型设计[J]. 系统仿真学报,2012,24(3):638-644.ZHENG Siyi,WANG Zhiliang,ZHANG Pengyi.Design of gazing geometrical model based on eyeball structure[J].Journal of System Simulation,2012,24(3):638-644.

[4]张鹏翼,王志良,郑思仪,等.使用立体视觉信息的视线追踪系统设计[J].北京邮电大学学报,2010,33(1):47-51.

ZHANG Pengyi, WANG Zhiliang, ZHENG Siyi，et al. A design of eye gaze tracking system using stereovision information[J].Journal of Beijing University of Posts and Telecommunications, 2010,33(1):47-51.

[5]朱博,迟健男,张天侠.视线追踪系统头动状态下的视线落点补偿方法[J].公路交通科技,2013,30(10):105-111.

ZHU Bo, CHI Jiannan, ZHANG Tianxia. Gaze point compensation method under head movement in gaze tracking system[J].Journal of Highway and Transportation Research and Development, 2013,30(10):105-111.

[6]CHUL Lee Eui, RYOUNG Park Kang.A robust eye tracking method based on a virtual eyeball model[J].Machine Vision and Applications,2009,20(5):319-337.

[7]ZHAO Qijie,ZHANG Guodong,CHENG Defu,et al.Relationship between light position and gaze identified parameters in infrared TV based eye gaze tracking system[J].Journal of System Simulation,2011,23(10):2239-2247.

[8]迟健男,王志良,张闯.视线追踪[M].北京：机械工业出版社,2011:164-229.CHI Jiannan,WANG Zhiliang,ZHANG Chuang.Eye tracking[M].Beijing:China Machine Press,2011:164-229.

[9]杨彩霞.基于近红外光源的非接触式视线跟踪技术研究[D].济南:山东大学,2012.

YANG Caixia. Research of remote gaze tracking technique with near IR illumination[D].Jinan: Shandong University,2012.

[10] 黄亚勤.基于视线跟踪技术的眼控鼠标研究与实现[D].成都:西华大学,2011.

HUANG Yaqin. The eye-mouse research and implementation based on eye gaze tracking technology[D].Chengdu: Xihua University,2011.

[11] 迟健男,张闯,陈凯,等.一种由粗及精的视线追踪系统平面视线参数检测方法[J].兵工学报,2012,33(8):902-911.

CHI Jiannan, ZHANG Chuang, CHEN Kai, et al. Planar gaze parameter detection in gaze tracking system with active infrared light source[J].ACTA ARMAMENTARII, 2012,33(8):902-911.

[12] 黄莹,王志良,涂序彦,等.一种可适应自然头动的视线跟踪系统的研制及应用[J].电子学报,2009,37(4):764-771.

HUANG Ying, WANG Zhiliang, TU Xuyan, et al. Development and application of a gaze tracking system adapting to natural head-movements[J].ACTA ELECTRONICA SINICA, 2009,37(4):764-771.

[13] SUN Jiande,YANG Caixia,LIU Ju,et al.Gaze tracking based on similarity between spatial triangles and two-step calibration[J].Electronics Letters,2011,47(4):254-255.

Gaze point compensation method based on Riemannian geometry in eye tracking system

JIN Chun1,2, LI Yaping1

(1. Wireless Transmission Key Laboratory, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R.China;2. Chongqing Jinou Science & Technology Development Co. , Ltd. ,Chongqing 400041,P.R.China)

Abstract:Aiming at the problem of poor robustness of gaze point estimation algorithm of un-contact eye tracking system, we modified the eye tracking system consist of single camera and two light sources. One novel gaze point compensation algorithm in Riemannian space was proposed in this paper based on the estimation algorithm of gaze point in space similar triangles. First we made the analysis of the influence of ocular cornea surface to the gaze point error based on eyeball structure. Then, according to the physiological characteristic of human eyes, the ocular cornea surface was modeled in the system of Riemannian geometry. The triangle constructed with the three shortest geodesics was presented to compensate the error of gaze point in Euclidean geometry eye tracking system. Finally the nonlinear polynomial model was also used to fit the error of eye visual axis and optical axis. In our experiment, the deviation of this algorithm is less than 1 centimeter both in horizontal and vertical directions. The result showed that the algorithm we proposed had significant effect on the compensation of gaze point.

Keywords：eye tracking; Riemannian geometry; similar triangles; visual axis; optical axis

DOI：10.3979/j.issn.1673-825X.2016.03.019

收稿日期：2015-05-01

修订日期：2015-12-14通讯作者：李娅萍840666078@qq.com

基金项目：高技术产业发展专项(渝发改技(2014)1177)

Foundation Item：The High Technology Industry Development Project(Chongqing Development and Reform Commission(2014)1177))

中图分类号：TP391.41;TN925

文献标志码：A

文章编号：1673-825X(2016)03-0395-05

作者简介：

金纯(1966-)，男，重庆人，教授，研究生导师，主要研究方向为无线通信、眼球追踪、人工智能、物联网等。E-mail: jinchun@jinoux.com。

李娅萍(1989-)，女，河南商丘人，硕士生，主要研究方向为眼球追踪、人工智能、物联网、无线网络等。E-mail:840666078@qq.com。

(编辑：王敏琦)