基于自适应随机共振的水下蓝绿光微弱信号检测
张建磊,张娟,朱云周,姚欣钰,吴倩倩,杨祎,贺锋涛
(1 西安邮电大学 电子工程学院,西安 710121) (2 中国科学院西安光学精密机械研究所,西安 710119)
0 引言
海洋作为地表广阔的一部分,拥有丰富的自然资源和矿产资源,为了有效地开发和利用这些资源,水下通信技术变得至关重要[1]。水下无线光通信(Underwater Wireless Optical Communication,UWOC)作为一种新型的水下通信技术,具有传输速率快、抗干扰能力强、可靠性良好、延时低等优势,在海洋资源开发等方面具有广阔的应用前景和发展潜力[2-3]。然而,光信号在传输过程中,海水的吸收和散射带来的衰减仍是限制UWOC 性能的一个重要因素[4]。另外,通信过程中受系统噪声的影响,当接收信号的功率较低时,噪声可能会淹没有效信号,使得接收端获取所需信息不准确,进而影响通信质量。海洋中海量数据的传输需求激发了研究者的热情,关于如何进一步提升通信速率和通信距离展开了众多研究。浙江大学FEI C 等[5]以450 nm 的半导体激光器(Laser Diode,LD)作为光源,采用自适应比特/功率负载离散多音频(Discrete Multitone,DMT)和Volterra 系列后置预编码器跟踪均衡器(TD-NE)技术,在UWOC 传输系统中实现了5 m/16.6 Gbps 的数据传输。中国科学技术大学WANG J M 等[6]提出并通过实验验证了一种以低成本绿色LD 作为光源,雪崩光电二极管(Avalanche Photodiode,APD)作为探测器,采用开关键控(On-Off Keying,OOK)调制技术的长距离高速UWOC 系统,可实现100 m/500 Mbps 的数据传输,且系统误码率为2.5×10-3。湖南师范大学CHEN M 等[7]使用蓝色发光二极管(Light-emitting Diode,LED)作为光源,设计了一个基于可编程逻辑门阵列(Field-programmable Gate Array,FPGA)芯片和DMT 收发器的水下可见光通信(Underwater Visible Light Communication,UVLC)系统,采用混合信道估计和多符号交织技术,实现了1.2 m/1.58 Gbit/s 的无差错实时信号传输。目前研究者们也通过信号检测技术改善水下通信系统性能。深圳市鹏城实验室的JIANG R 等[8]提出了一种基于单光子雪崩光电二极管(Single Photon Avalanche Photodiode,SPAD)UWOC 系统的深度学习辅助信号检测方案,解决了水下光学通道和SPAD 造成的信号失真问题,降低了误码率。浙江大学的CHEN X 等[9]提出了一种联合数字信号处理方案,通过结合部分响应整形和网格编码调制(Trellis Coded Modulation,TCM)技术,抑制均衡器引起的噪声并减小信号失真。结果显示,该方案在500 Mbps 的数据速率下,最小接收光功率为-29.8 dBm,且误码率为3.8×10-3。北京邮电大学的ZHANG J L 等[10]在接收端采用了7 分频最大似然序列估计(Maximum Likelihood Sequence Estimation,MLSE)检测技术,最大可用比特率提高了1.6 Gb/s,而可用带宽限制在0.12 GHz 左右。近年来,研究者们多采用非线性系统实现低信噪比信号检测,随机共振(Stochastic Resonance,SR)[11-13]利用噪声、输入信号和系统共同作用,产生一种协同效应,不仅提高了输出信噪比,而且检测到了有用信号,备受研究者们关注。MA L 等[14]将随机共振引入到UWOC 信号增强中,仿真分析了噪声以及系统参数对误码率的影响,结果表明随机共振系统相较于低通滤波器对UWOC 信号增强更有优势。FENG Z 等[15]提出了一种基于随机共振非线性动力学的自适应随机共振方案,将尺度变化引入到随机共振信号检测方法中,通过对系统噪声方差的估计实现了系统参数估计。但为了更好地适应不同环境中的噪声和干扰,参数选取需在不同信噪比下人为设置。针对系统参数选择不够灵活,不能充分发挥随机共振信号检测优势的问题,本文提出了基于多策略融合粒子群(Multi-strategy Fusion Particle Swarm Optimization,MFPSO)算法的自适应随机共振水下蓝绿光微弱信号检测方法。通过将信号输出信噪比作为目标函数,动态调整系统模型参数,实现参数的最优选取,同时搭建UWOC 实验系统验证方法的可行性。
1 基本原理
1.1 水下光信道模型
在水下信道链路质量的研究过程中,光强可以用比尔-朗伯定律[16]描述为
式中,Pr为接收光功率,Ps为发射光功率,c(λ)为海水总衰减系数,λ为光波长,d为水下通信距离。
海水总衰减系数可以表示为吸收系数和散射系数之和,即
式中,a(λ)为吸收系数,吸收系数受波长影响较大,会引起信号振幅下降,造成接收机灵敏度降低并产生噪声;b(λ)为散射系数,受悬浮粒子密度的影响较大,其引起的多径效应会导致码间干扰。
1.2 双稳态随机共振
随机共振是一种微弱特征信号在非线性系统的作用下通过噪声转移机制以实现信号增强的方法。其基本模型如图1 所示。

图1 随机共振的基本模型Fig.1 Basic model of stochastic resonance
该模型主要包含三个要素:输入信号、噪声、非线性系统。其经典模型为双稳态随机共振系统,可用Langevin 方程[17-19]描述为
式中,a、b为系统模型的两个参数。当没有噪声以及输入信号时,U(x)势函数曲线如图2 所示。可以看出系统有两个稳态点以及一个不稳定点xb=0,xw称为势函数的势阱,xb称为势函数的势垒。势垒到势阱的高度差称为势垒高度,即

图2 双稳态随机共振系统势函数Fig. 2 Potential function of a bistable stochastic resonance system
当只有外部信号施加到系统时,如果输入信号十分微弱,即信号幅值A小于系统幅值Ac,粒子不能越过势垒,仅仅在单侧势阱内进行振动,其所处的单侧势阱位置取决于初始状态。只有信号幅值A大于系统幅值Ac时,粒子才能从发生势阱间跃迁。
当信号x(t)和噪声n(t)同时施加到系统时,并且输入信号、噪声和非线性系统相匹配时,即使信号幅值小于系统幅值,粒子也可以跨越势垒并在两个势阱之间来回切换,从而引发SR 现象。
实际求解双稳态系统的Langevin 方程时,采用四阶Runge-Kutta 方程[20]离散化来获得输出响应,即
式中,h为龙格-库塔算法的步长,xn为输出信号x(t)的第n个采样值,pn为混合信号(输入信号s(t)和输入噪声n(t)之和)的第n个采样值。使用Runge-Kutta 之前,需先求出SR 参数的最优取值。
2 基于MFPSO 算法的随机共振
2.1 传统粒子群算法
粒子群算法是一种基于鸟类觅食行为的启发式搜索算法。与其他仿生学算法相比,该方法需要调整的参数较少,易于实现,因此被广泛应用于各种多目标优化问题中。其具体过程是将被优化目标看作一群随机粒子,这些粒子在解空间进行搜索,每一次迭代过程中,粒子根据自身经验和群体信息来更新位置和速度,以便寻找更好的解。通过不断迭代搜索,逐渐向最优解靠拢。
传统PSO 算法[21-23]可以表示为:假定在D维(D=1,2,…,d)搜索空间中有一个粒子数目为M的粒子群,每个粒子i的位置和速度分别用xi=(xi1,xi2,…,xid)和vi=(vi1,vi2,…,vid),i=1,2,…,M表示。则算法的度和位置更新公式分别为
式中,t为当前迭代次数;w为惯性权重;c1、c2为加速度系数,分别表示个体学习因子和社会学习因子,用以对Pi(t)和Pg(t)加权;r1,r2是[0,1]范围内的两个随机值;Pi(t)、Pg(t)分别为第i个粒子在第t次迭代中的个体最优位置以及全局最优位置。
2.2 MFPSO 算法
针对传统粒子群算法易陷入局部最优而导致收敛精度低和不易收敛的问题,提出了MFPSO 算法。引入自适应惯性权重动态调整粒子的局部搜索能力与全局搜索能力,加快收敛速度;采用邻域探测在粒子进化过程中加强对局部极值位置邻域的探测,增强算法的求精能力;应用柯西变异和反向学习策略对最优解进行变异扰动,有效提升算法逃离局部空间的能力。
2.2.1 自适应惯性权重
传统粒子群算法局部搜索能力差,前期收敛速度快而后期较慢,降低了解的精度。研究表明,惯性权重w的取值对算法的全局和局部搜索能力有显著影响。惯性权重w较小时,粒子的局部搜索能力较强,在搜索空间中更容易收敛到局部最优解,但全局搜索能力较弱;惯性权重w较大时,全局搜索能力较强,在搜索空间中更容易跳出局部最优解,寻找并探索新的区域,但局部搜索能力较弱。自适应惯性权重可以在算法的不同阶段平衡全局和局部搜索能力,从而影响搜索速度。因此采用使用较广泛的线性权重递减策略,其描述为
式中,wmax、wmin分别代表w的最大值和最小值,Nmaxiter为最大迭代次数。
2.2.2 邻域搜索
PSO 算法在粒子进化过程中,通过粒子的位置和速度更新来实现对Pi(t)和Pg(t)的更新,并未考虑到迭代末期算法在接近最优解时收敛速度降低甚至出现停止收敛的情况,此时得到的结果可能并不是全局最优解。因此引入邻域搜索[24]策略,在进化初期搜索半径较大,随着迭代次数增加,搜索半径逐步减小,使粒子群算法在进行局部搜索时能够更加细致准确定位到最优解,一定程度上大大增强了算法的寻优精度与准确度。
在Nmaxiter次迭代过程中,粒子在第t次迭代时先产生随机数P∈[0,1],计算邻域搜索半径系数Rk为
如果P<Rk,则使用式(11)计算出搜索半径rk,并通过式(12)计算得到新的最全局最优位置Pl,最后采用式(13)和(8)进行速度和位置更新;否则按式(7)和(8)进行速度和位置更新。
式中,rand()表示产生(0,1)之间的随机数。
2.2.3 变异机制
变异扰动策略通过引入随机性和多样性以打破粒子群算法陷入局部最优的情况,有效提升算法逃离局部空间的能力。在粒子迭代过程中,如果Imax寻优得到的最优解相同,则认为算法可能陷入了局部最优,其中Imax的取值需根据问题规模进行合理设定。Imax过大,早熟收敛的判断可能不准确;Imax过小,大大增加了算法复杂度。设计一个计数器,用以判断当前为止是否停止迭代。若连续两次迭代最优解Pg(t)无变化,则计数器Tcount加1,否则将其清零。当满足Tcount≥Imax,说明算法可能已经陷入局部最优,通过反向学习机制去搜索空间内对应的反向解,即产生新解,从而有效扩大粒子的搜索区域;通过柯西变异算子在最优解位置进行扰动,得到新解,有效改善算法跌入局部最优区域的缺陷。采取反向学习和柯西变异两种策略相融合的方式对局部最优解变异扰动,根据选择概率Pθ来决定具体策略的选择,计算公式为
产生(0,1)之间的随机数R,如果R<Pθ,按照反向学习策略[25]进行最优解位置更新,其数学表达式为
式中,Pg'(t)为第t代最优解的反向解,xmax、xmin分别是位置x的上下界,r是服从(0,1)标准均匀分布的随机数矩阵,b1表示信息交换控制参数,公式为
如果R≥Pθ,按照柯西变异扰动策略[26]进行最优解位置更新,其数学表达式为
式中,cauchy(0,1)为标准柯西分布,该分布随机变量生成函数为
式中,η的取值与ς有关
使用上述算法进行变异更新后,无法确定更新后新位置的适应度值是否比更新前更优,所以采用策略进行比较,即
式中,f(xi(t+1))为粒子位置更新后新位置的适应度值,f(Pg)为粒子最优位置的适应度值。
2.3 基于MFPSO 算法的自适应随机共振
提出一种MFPSO 算法对SR 系统参数进行寻优,并采用四阶龙格库塔数值仿真求解输出响应,进而实现弱光信号检测。相较于以往固定参数调节SR 微弱信号检测方法,系统参数的选取更加灵活。通过设定系统的输出信噪比作为评选指标,合理设置最大迭代次数以及寻优过程中所需参数范围,在满足最大迭代次数范围内寻找使得输出信噪比最大的最优系统参数组(a,b)。基于MFPSO 算法的自适应调节随机共振流程如图3 所示,具体步骤为

图3 基于MFPSO 算法的自适应随机共振流程Fig. 3 Flow chart of adaptive stochastic resonance based on MFPSO algorithm
1)噪声信号预处理。实际深海水域中光信号的传输频率和采样频率较大,远不能满足随机共振绝热近似条件,因此需使用二次采样[27]对噪声信号进行预处理。
2)初始化算法参数。设定种群数量M,最大迭代次数Nmaxiter,惯性权重wmax、wmin,加速度系数c1、c2,连续最优解相同次数Imax以及优化参数(a,b)的取值范围,并初始化粒子种群位置和速度,判断是否符合预设条件,且每个位置对应一组随机共振系统参数(a,b),根据此参数组可计算目标函数值。
3)计算适应度值。计算每个粒子适应度fi,将其作为个体最优Pi,并把初始种群粒子个体最优作为全局最优Pg。
4)更新粒子的速度和位置。产生随机数P∈[0,1],根据式(10)计算Rk,并比较P和Rk的大小关系。当P<Rk时,根据式(10)~(12)计算出Pl,并按式(13)和(8)进行速度和位置更新;当P≥Rk时,继续比较Tcount与Imax的关系:①当Tcount≥Imax时,计算选择概率Pθ。如果随机数R<Pθ,按照反向学习策略式(15)~(17)更新最优解,否则按照柯西变异策略式(18)对最优解进行变异扰动,产生新解。②当Tcount<Imax时,按式(7)和(8)进行速度和位置更新。
5)评估、更新每个粒子的适应度值。计算个体xi的适应度值fi,并判断fi与Pi大小关系。如果fi较优,将其赋给Pi,否则不进行更新。并对全局最优Pg进行类似的操作。
6)判断是否满足终止条件。如果种群达到预设的最大迭代次数,则停止迭代计算,输出最优参数组(a,b),否则跳至步骤4)继续迭代。
7)参数带入。将步骤6)所得(a,b)代入双稳态模型,利用四阶Runge-Kutta 求解输出响应,实现弱光信号的检测。
3 仿真分析
在所建立的UWOC 弱信号检测系统下进行仿真,以评估所提MFPSO 算法的可行性和有效性。仿真信号使用易于分析的双极性不归零信号,理论研究表明参数a、b的取值影响随机共振的效果,考虑到导频信号的特殊性质,即在发送端插入若干已知数据并且能够在接收端被准确提取出来,可以作为一个可靠的参考信号来进行参数估计,并为后续的信号处理提供重要参考。使用MFPSO 算法进行自适应处理时,引入导频信号,通过对导频序列进行自适应随机共振得到最优系统参数,进一步使用所得最优参数处理信息序列,统计误码率。导频信号长度的选择一定程度上影响着寻优的速度和精度,导频长度过长导致系统开销较大,过短可能导致寻优不准确。此处选取了103个码元进行参数自适应寻优,选取105个码元进行误码统计,其中,每个码元的采样点数为50。参数a和b的取值范围为[0,5],输入信号信噪比为SNRin=-5 dB,PSO 和MFPSO 算法的参数设置如表1。

表1 PSO 和MFPSO 算法的参数设置Table 1 The parameter settings of PSO and MFPSO algorithms
图4 对比了输入信噪比SNRin=-5 dB 下PSO 和MFPSO 算法完成参数寻优的结果收敛。由图4(b)可以看出使用MFPSO 算法后经23 次迭代便可找到系统最优参数,此时对应a=1.279 2,b=2.381 3,输出信噪比为6.475 2 dB,相比于输入信噪比提高了11.475 2 dB,并且相较于PSO 算法大大提升了收敛速度。使用MFPSO算法后,粒子的位置最初随机分布在解空间中,随着迭代的进行,各个粒子逐渐往全局最优粒子位置靠近。
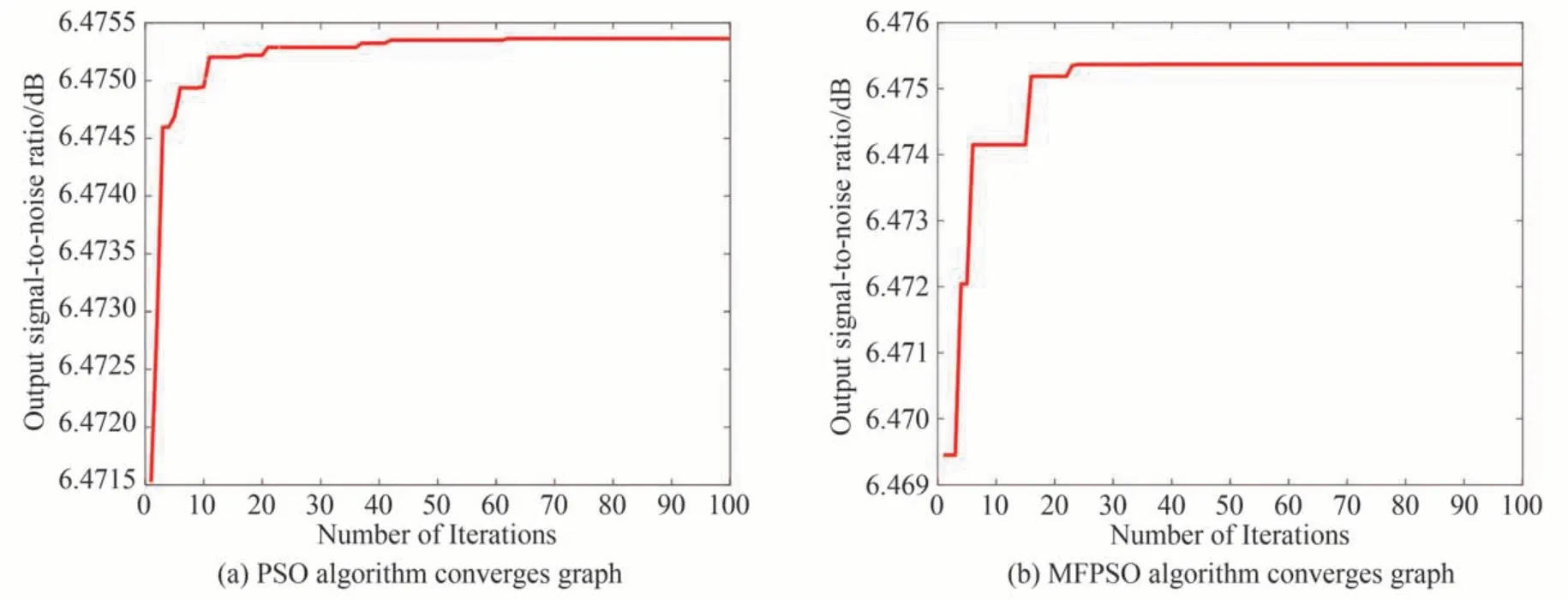
图4 系统参数寻优结果收敛Fig. 4 Convergence of system parameter optimization result
基于表1 参数,使用MFPSO 算法处理含有高斯白噪声的双极性不归零信号,其结果如图5(a)。图5(b)、(c)分别为使用所提算法前后的眼图。由图5(a)可知,双极性不归零信号经过水下信道后出现了严重的低信噪比现象,导致输入信号被淹没在噪声中无法判决,使用基于MFPSO 算法的自适应随机共振检测方法处理后,接收信号的时域波形图明显改善。对比图5(b)、(c),也可以发现发送信号经过水下信道后受到了严重的干扰和失真,导致相应的眼图无任何规律,但采用所提算法处理后,接收信号的“眼睛”张大,信号质量变好。

图5 基于MFPSO 算法处理的含有高斯白噪声的双极性不归零信号及处理前后相应的眼图Fig. 5 Bipolar non-return-to-zero signals with Gaussian white noise processed by MFPSO algorithm and corresponding eye images before and after processing
图6 对比了不同输入信噪比下不经过随机共振(NO-SR)、固定参数随机共振(a=1、b=1,F-SR)、基于PSO 和基于MFPSO 的自适应随机共振(PSO-SR、MFPSO-SR)误码率性能。其中,码元数目设置为105,每个码元的采样点数为50 个。从图中可以看出,当信噪比小于-4 dB 时,NO-SR 检测方案信号的误码率始终高于10-2,尽管随着信噪比的增加误码性能有所改善,但始终差于其余三种检测方案。使用随机共振能够降低通信系统的误码率,但F-SR 参数的选取依赖于人为选定,导致误码性能提升有限。自适应随机共振能够根据系统性能动态调整模型参数,显著改善系统误码率,尤其在-6 dB 以上,改善效果十分明显。相比于PSO-SR,所提MFPSO-SR 收敛速度更快,寻优结果更精确,产生的误码率更低。
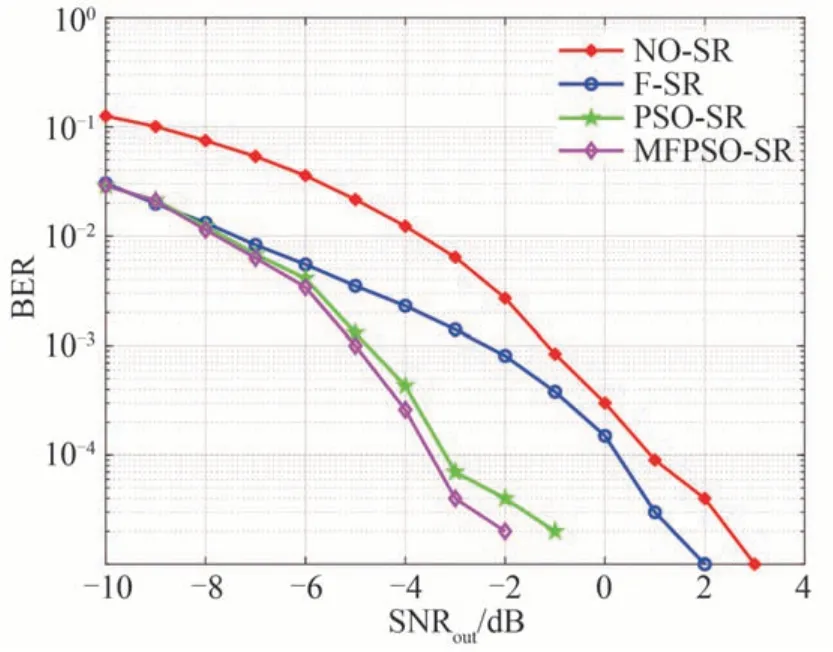
图6 不同检测方案下的误码率随信噪比变化情况Fig. 6 Changes of bit error rate with SNR under different detection schemes
4 实验分析
4.1 实验装置
为了进一步验证所提算法在UWOC 系统中的性能,搭建了如图7 所示的实验系统。在发射端,采用FPGA 开发板(EP4CE10F17,AC609)发送阶数为215的伪随机信号,并驱动绿色激光二极管产生光信号(波长为520 nm,发射功率为1.46 mW)。经过准直透镜后,从LD 发出的绿光经过一个3 m×0.5 m×0.5 m 的实验水箱(水深0.35 m)传输后达到接收端。首先,向实验水箱加入5 g 牛奶作为掺杂剂。其次,在水箱中距离左侧0.5 m、1.5 m、2.5 m 处分别放置3 个加热装置(水的初始温度为20 ℃,加热至30 ℃)以模拟温度梯度。最后将气泵装置连接到微孔陶瓷板上,以模拟水下气泡现象。其中,气泵出气量设置为1.5 L/min,气泵机出气孔放置在水箱中间,距离水箱左右两侧各1.5 m。最终,对不同温度下的衰减系数取平均值,所得结果为0.78 dB/m。在接收端,采用光电探测器APD430A(/M)接收光信号,并使用示波器(MSO5204B Tektronix)进行信号采集,最后在PC 端进行离线处理,恢复出原始信号。
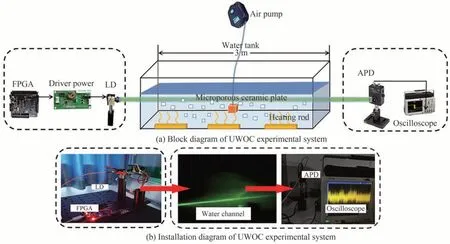
图7 水下无线光通信实验系统Fig.7 Underwater wireless optical communication experimental system
4.2 实验结果
实验过程中,设置码元传输速率为1 MHz,且每个码元的采样点数为50,PSO 和MFPSO 算法的参数选择和仿真分析部分保持一致。图8 为接收信噪比为-1.7 dB 时,使用MFPSO 算法完成参数a、b的寻优结果,此时对应系统参数a=0.000 8,b=3.146 8。图9 为基于该参数使用MFPSO 算法处理实验采集数据结果,此时误码率为2×10-4。相较于NO-SR 和F-SR(a=0,b=3),误码率提升了1 个数量级和0.5 个数量级以上,原因是仿真信道状态只考虑了高斯白噪声,实验过程中信道环境复杂,光信号在水下传输时,噪声并不完全符合高斯白噪声模型,另外实验过程中使用的探测器本身的噪声并不是传统意义上的零均值高斯白噪声,导致实验误码率高于仿真结果。

图8 基于MFPSO 算法完成参数a、b 的寻优(SNR=-1.7 dB)Fig. 8 Optimization of parameters a and b based on MFPSO algorithm (SNR=-1.7 dB)

图9 基于MFPSO 算法处理的实验采集数据(SNR=-1.7 dB)Fig. 9 Experimental data collected based on MFPSO system processing (SNR=-1.7 dB)
5 结论
针对水下无线光通信中低信噪比信号检测问题,本文提出自适应随机共振水下蓝绿光微弱信号检测方法。分析了随机共振的产生条件,采用多策略融合粒子群算法动态调节随机共振系统参数,实现系统参数自适应估计。通过引入自适应惯性权重、邻域探测与变异机制相结合的混合策略,改进了传统粒子群算法易陷入局部最优导致收敛精度低和不易收敛的问题。仿真了含有高斯白噪声的双极性不归零信号在不同检测方案下的误码性能,结果表明,相比不经过随机共振、固定参数随机共振,自适应随机共振检测方案具有明显优势。为验证方法的有效性,搭建了UWOC 系统,所提基于多策略融合粒子群算法的自适应随机共振水下蓝绿光微弱信号检测方法在接收信噪比为-1.7 dB 时,误码率可达2×10-4,进一步验证了自适应随机共振在水下蓝绿光微弱信号检测方面的有效性。

