基于改进Morozov 偏差原理的动态光散射粒度反演
王保珺,申晋,李鑫强,王钦,刘伟,王雅静,明虎
(山东理工大学 电气与电子工程学院,淄博 255049)
0 引言
动态光散射(Dynamic Light Scattering,DLS)技术是测量颗粒粒度分布(Particle Size Distribution,PSD)的有效方法[1-2],该技术以其快速、准确和非接触等优点[3]在材料[4-5]、化工[6]、食品[7-8]、医药[9-11]等领域得到广泛应用。DLS 技术通过对散射光强信号进行自相关运算获得光强自相关函数(Autocorrelation Function,ACF),通过反演光强ACF 获得待测颗粒的PSD。反演ACF 需要求解第一类Fredholm 积分方程,该方程是一典型的病态方程,测量数据中的微小误差或噪声均会导致所求PSD 的显著变化。为提高PSD 反演的准确性,研究人员已提出了多种反演方法,包括奇异值分解法[12]、CONTIN 法[13,14]、非负约束最小二乘法[15,16]和Tikhonov 正则化方法[17]等。这些方法各有其特点,其中的Tikhonov 正则化方法由于不受粒度分布的限制,具有良好的适应性,在DLS 测量中得到了广泛的应用。该方法通过引入稳定泛函改善病态性,由正则化参数控制稳定泛函的修正程度,因此对反演结果有重要影响[18]。如果选择的正则化参数过小,反演的PSD中会出现振荡和虚假峰,而正则化参数过大,则会出现过于平滑的反演结果[19]。选择正则化参数的主要方法包括L-curve 准则[20-21]、Morozov 偏差原理(Morozov's Discrepancy Principle,MDP)[22-23]以及广义交叉验证准则(Generalized Cross Validation,GCV)[24,25]等。
在DLS 测量技术中,进行正则化反演通常采用L-curve 准则选取正则参数。2012 年,刘晓艳[26]采用Lcurve 准则进行正则化反演颗粒粒度分布,研究了DLS 技术对散射角的依赖关系。2016 年,林承军等[27]将多参数正则化用于前向散射测量中的粒度反演,降低了正则化算法带来的振荡和负值。2022 年,LIU Z 等[28]和韩锦壮等[29]分别采用L-curve 准则选取正则参数进行了流动颗粒DLS 粒度反演,文献[28]对L-curve 准则和GCV 两种正则参数选取方法进行了比较,认为在噪声水平较低时,GCV 方法选取正则参数的反演结果优于L-curve 准则的结果,而当噪声水平较高时,L-curve 准则的反演效果则优于GCV 方法。文献[29]通过条件预优处理降低了正则化对流速增加的敏感性,从而改善了流动颗粒DLS 反演的性能指标。
L-curve 准则是通过解的向量模间接引入稳定性分析,但其在宽粒度分布条件下通常不能得到准确的PSD 反演结果。MDP 方法可依据电场ACF 的噪声水平选取正则参数以适应不同的粒度分布,但原始数据噪声水平通常是未知的,这一条件限制使其难以在DLS 的实际测量中得以应用。与窄粒度分布颗粒的DLS反演相比,宽分布颗粒反演难以获取与之相适应的正则参数。为解决宽粒度分布反演时正则参数不易准确选取的问题,本文提出基于改进Morozov 偏差原理的MDP-GA 正则参数求取方法,即采用小波包分解(Wavelet Packet Decomposition,WPD)结合MDP 的方式建立迭代判据,利用遗传算法(Genetic Algorithm,GA)迭代求取正则参数,较好地解决了宽分布颗粒DLS 反演中正则参数不易准确选取的难题。
1 动态光散射与正则化反演
对于振幅满足高斯分布的散射场,光强ACFG(2)(τ)与电场ACFg(1)(τ)间满足Siegert 关系,即
式中,τ为延迟时间,B为测量基线,β为相干因子,且β≤1。对于多分散颗粒体系,g(1)(τ)表示为
式中,G(Γ)为衰减线宽分布函数,Γ为衰减线宽,可由Stokes-Einstein 公式求得。
式中,d为颗粒粒径,KB、T、η、λ0、n和θ分别为Boltzmann 常数、绝对温度、介质粘度系数、入射光波长、悬浮介质的折射率和散射角度。
式(2)的离散形式为
式中,τj为离散的延迟时间,N和i分别为离散粒度的总点数和第i个离散点,M和j分别为光子相关器的总通道数和第j通道,f(di)为的粒度分布,满足通过衰减线宽—平移扩散系数—颗粒粒度关系,可求得颗粒粒度分布f(d)。
式(4)的矩阵形式为
式中,g为归一化电场ACF 的向量形式,其元素为g(1)(τj),A为电场ACF 数据对应的核矩阵,其元素为exp(-Γiτj),f是由离散的PSD 组成的向量,其元素为f(di)。
式(5)是病态方程,通常采用Tikhonov 正则化方法将其求解转化为未知函数的约束优化问题,即
式中,M、α、‖·‖和‖Lf‖分别为稳定泛函、正则参数、欧几里得范数和惩罚因子。正则矩阵L选用二阶差分矩阵,α控制解的稳定性和准确性。
2 MDP-GA 正则参数选取方法
本文提出的基于改进Morozov 偏差原理的MDP-GA 方法,是一种以GA 全局寻优求取正则参数的方法。该方法在正则参数经验范围生成初始种群,利用WPD 求出电场ACF 的噪声分量,并将该分量的噪声水平代入MDP 判据,建立适应值函数。通过保留每代种群中适应值最优的个体,来保证迭代的进化方向,进而对种群做交叉和突变运算,生成下一代种群。
作为待求正则参数的随机初始值,种群中的初始个体目标变量可表示为
式中,λmax和λmin分别为目标变量允许的最大和最小值,在DLS 正则参数选取中对应值分别取20 和0,Rand为[0,1]区间内的随机数。
为评价种群中个体的优劣,根据MDP 判据‖Afα-g‖2-δg2=0 建立适应值函数f,表示为
式中,δg为g的噪声水平,由WPD 给出。在本代种群做交叉和突变运算前,需要保留本代的最优个体λbest,即本代种群中适应值最大的个体。每两个个体都有发生交叉的概率,发生交叉的两个个体由式(9)求得。
式中,λa、λb为产生交叉的两个个体,β为交叉发生的概率。每个个体都有发生突变的概率,设第t代种群为(λ1…λi…λm),若仅λi发生突变,则t+1 代种群变为(λ1…λi'…λm),λi'表示为
3 模拟数据反演
采用半对数正态分布模型模拟单峰PSD,模拟实验条件为:分散介质折射率n=1.331 6,入射光在真空中的波长λ=632.8 nm,绝对温度T=298.15 K,介质粘度系数η=0.89 mPa·s,Boltzmann 常数KB=1.380 7×10-23J/K,相干因子β=0.7,基线B=1,PSD 的离散点数设定为M=100。
式中,Di、Dg和σ分别为离散的颗粒粒径、标称粒径和标准偏差,相应的G(2)(τ)数据通过式(1)和式(5)获得,表1 为两种不同分布宽度的400 nm 颗粒的PSD 模拟参数。

表1 PSD 的分布参数和属性Table 1 Parameters and properties of the simulated PSD
为接近实测情况,在模拟的光强ACF 中加入了高斯噪声,含噪光强ACF 可表示为
式中,n(τ)和δ分别为高斯随机噪声和噪声水平。
粒度反演时,首先由式(1)求得g(1)(τ),通过反演g(1)(τ)求取颗粒粒度。为评估反演结果,引入峰值位置相对误差(EP)和分布误差(VE)两个性能指标。
式中,P表示峰值位置处的粒径,下标true 和meas 分别表示真实值和反演值。
图1 为不同噪声水平下采用L-curve 准则和MDP-GA 两种正则参数选取方法对400 nm 窄分布颗粒的反演结果。图2 为400 nm 宽分布颗粒的反演结果。表2 给出了对应图1 和图2 反演结果的性能指标和两种算法的运行时间T。

图1 窄分布400 nm 的反演结果Fig.1 Inversion results of 400 nm narrow PSD


图2 宽分布400 nm 的反演结果Fig.2 Inversion results of 400 nm broad PSD

表2 PSD 反演的性能指标Table 2 Performance index of PSD inversion
从图1和表2可以看出,对于400 nm 窄分布颗粒,两种参数选取方法得到的反演结果相同。对于400 nm 宽分布颗粒,由图2 可知,在δ=10-5的噪声水平下,L-curve 准则反演结果的峰值位置向粒径增大方向偏移。随着噪声增加,在δ=10-4和δ=10-3噪声水平下,该方法所得分布中小粒径位置出现了虚假峰,且主峰分布变窄,峰值高于实际峰高。当噪声增加到通常认为的极限水平δ=10-2时,两种方法反演得到的PSD 都出现峰宽变窄且峰值位置向粒径减小方向偏移的现象。对照表2 可以看出,在δ=10-5、δ=10-4和δ=10-3等较低或常规噪声水平下,MDP-GA 方法均给出优于L-curve 准则的峰值误差和分布误差指标。同时,在表2 中也能看到,相对于L-curve 准则方法,MDP-GA 方法的运算时间有明显增加。考虑到DLS 测量时间通常为数分钟,因此,PSD 反演时间增加不足1.5 s,对测量不会产生影响。
4 实测数据反演
实验数据取自自行研制的DLS 测量实验平台(如图3),测量装置由波长为532 nm 的固体激光器(MGL-III-532 nm-15 mW)、光电探测器(CH326)和512 通道的数字相关器组成。测量的散射角度为90°,采用单模光纤探针接收散射光,样品池温度控制在298.15 K,实验样品颗粒按分布的宽窄分为两类。其中光纤探针由数值孔径0.12、纤芯直径3.5 μm 的单模保偏光纤和一个0.25 节距自聚焦透镜耦合组成,透镜发散角为2 mrad,光束直径为0.4 mm。

图3 实验装置示意Fig.3 Schematic of the experimental apparatus
4.1 窄分布粒度反演
两个窄分布样品分别为由(31±3) nm(Duke Scientific,3 030 A)和(203±5) nm(Duke Scientific,3 200 A)标准聚苯乙烯乳胶颗粒制备,所用分散剂为去离子蒸馏水,折射率和粘度系数分别为1.330 和0.891 mPa·s。两种样品颗粒的光强ACF、电场ACF、电场ACF 中的噪声分量和PSD 反演结果如图4、图5。表3 为反演结果的性能指标。
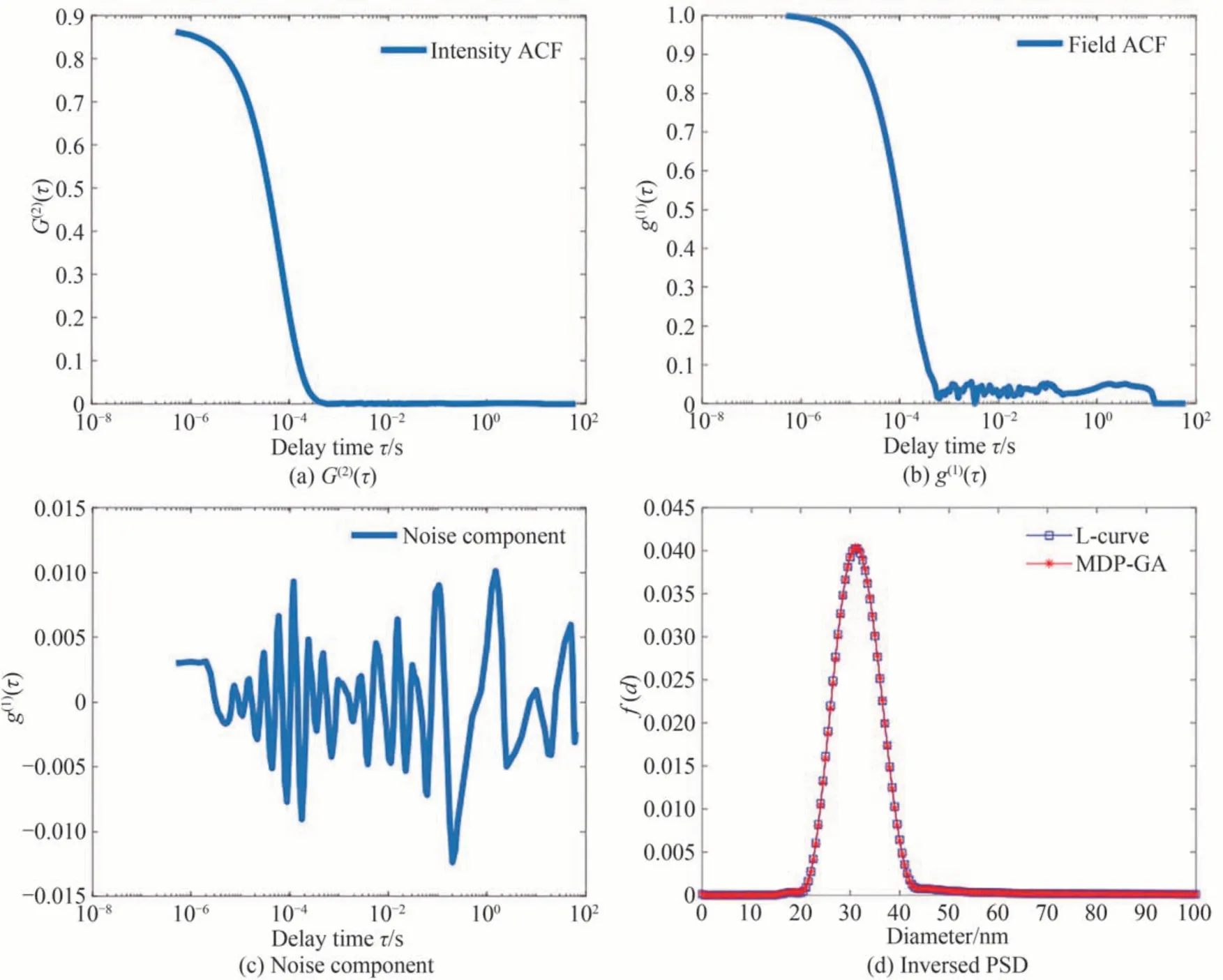
图4 31 nm 聚苯乙烯乳胶颗粒的G(2)(τ)、g(1)(τ)、噪声分量以及反演结果Fig.4 G(2)(τ), g(1)(τ), noise component and inversion results of 31 nm standard polystyrene latex particles
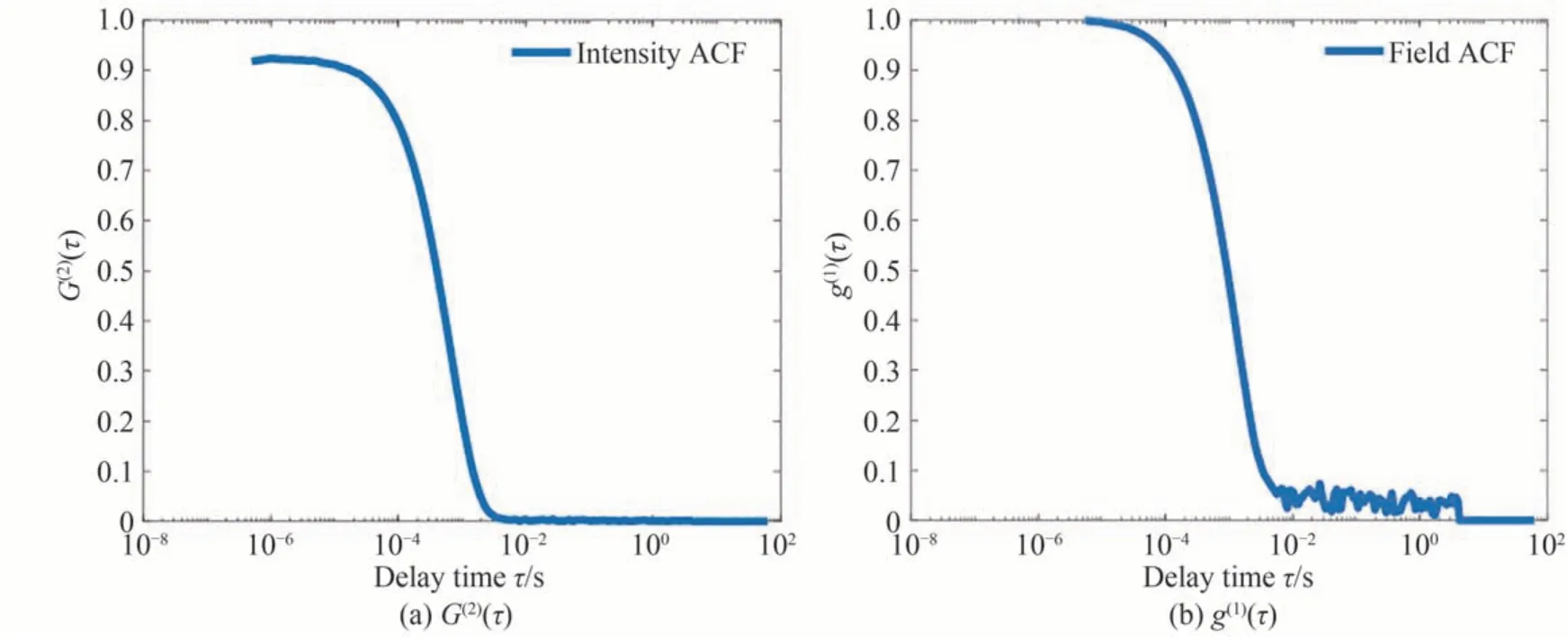
图5 203 nm 聚苯乙烯乳胶颗粒的G(2)(τ)、g(1)(τ)、噪声分量以及反演结果Fig.5 G(2)(τ), g(1)(τ), noise component and inversion results of 203 nm standard polystyrene latex particles

表3 标准聚苯乙烯乳胶颗粒反演的性能指标Table 3 Performance index for inversion of standard polystyrene latex particles
从图4(d)和图5(d)可以看出,对于31 nm 和203 nm 两种窄分布颗粒,采用两种正则参数选取方法所得的反演结果几乎无差异,表3 给出的两种方法所得的平均粒径相同。对比图4(a)、5(a)与图4(b)、5(b)可以看出,目测良好的光强ACF 数据,经Siegert 关系式中的开平方运算,会在求取的电场ACF 中明显放大。图4(c)和图5(c)表明,放大后的噪声随延迟时间增加而增大,从中可以看出光强ACF 中的噪声对反演结果的作用和根据噪声调节正则化强度的重要性。
4.2 宽PSD 反演
两个宽分布样品分别为由纳米级金刚石微粉(Nanodiamond)和钛酸钡(BaTiO3)制备。为评估反演结果,采用重复性误差(δr)作为被测颗粒的性能评价指标。
式中,xi表示第i次测量得到的峰值粒径,xˉ代表平均峰值粒径。由两种样品得到的光强ACF、电场ACF、电场ACF 中的噪声分量和PSD 反演结果如图6、7。表4 为进行6 次测量的峰值重复性误差。

图6 纳米金刚石微粉的G(2)(τ)、g(1)(τ)、噪声分量以及反演结果Fig.6 G(2)(τ), g(1)(τ), noise component and inversion results of nanodiamond particle system

表4 宽PSD 反演的性能指标Table 4 Performance index of wide PSD inversion
从表4 可以看出,对于纳米级金刚石微粉和钛酸钡颗粒,MDP-GA 方法均给出了低于L-curve 准则的峰值重复性误差,在图6(d)给出的L-curve 准则方法反演纳米级金刚石微粉所得PSD 中,小粒径位置出现了虚假峰。结合模拟数据的反演结果可以看出,对于窄分布颗粒,两种方法选取正则参数的反演结果没有明显差别,但对于宽分布颗粒,MDP-GA 方法所得反演结果的峰值误差、分布误差和重复性误差均低于L-curve 准则方法。需要说明的是,图6(a)和图7(a)给出的光强ACF 中的纵轴截距较高,这是由于实测工业颗粒中存在混入大颗粒或颗粒聚集等引起ACF 基线抬升所致,在图6(b)和图7(b)给出的电场ACF 的长延迟时段可清晰看到。

图7 钛酸钡颗粒的G(2)(τ)、g(1)(τ)、噪声分量以及反演结果Fig.7 G(2)(τ), g(1)(τ), noise component and inversion results of BaTiO3 particle system
5 结论
本文提出了基于改进Morozov 偏差原理的MDP-GA 正则参数选取方法,该方法可以显著改善宽粒度分布颗粒体系的DLS 正则化反演效果。首先,通过小波包分解求出电场ACF 的噪声分量,得到其噪声水平。然后,通过MDP 建立适应值函数,在正则参数经验范围内生成初始种群。最后,将适应值函数与初始种群带入遗传算法,通过全局寻找最优适应值对应的参数值作为正则参数。模拟与实测数据的反演结果表明,对于窄分布颗粒体系,所提MDP-GA 方法与L-curve 准则方法的反演结果无显著差异,对于宽分布颗粒体系,MDP-GA 方法反演结果的性能指标优于L-curve 准则,避免了正则参数选取不当导致的PSD 中出现虚假峰和峰值偏移情况,得到了更为准确的宽分布颗粒体系的反演结果。鉴于复杂粒度分布的准确测量需要采用多角度DLS 方法,利用MDP-GA 方法在多角度DLS 反演中进行正则参数选取,将是本研究后续的主要工作。

