“三招”解决一道解三角形长度比值问题

李娟

【摘要】解三角形问题是高考数学中的重要考点，題型多样，主要研究三角形中的角、边等几何量的范围或者比值大小，涉及知识点广泛.本文根据实例探讨此类问题的妙解妙法，以供读者参考.

【关键词】高中数学；解三角形；正、余弦定理

在做此类题目时，首先要对基本的知识点有所掌握，如正、余弦定理和正、余弦公式以及基本的三角代换等等.有时还需要借助三角函数利用导数进行研究.下面就根据一道例题来谈谈此类解三角形长度比值问题的解法.

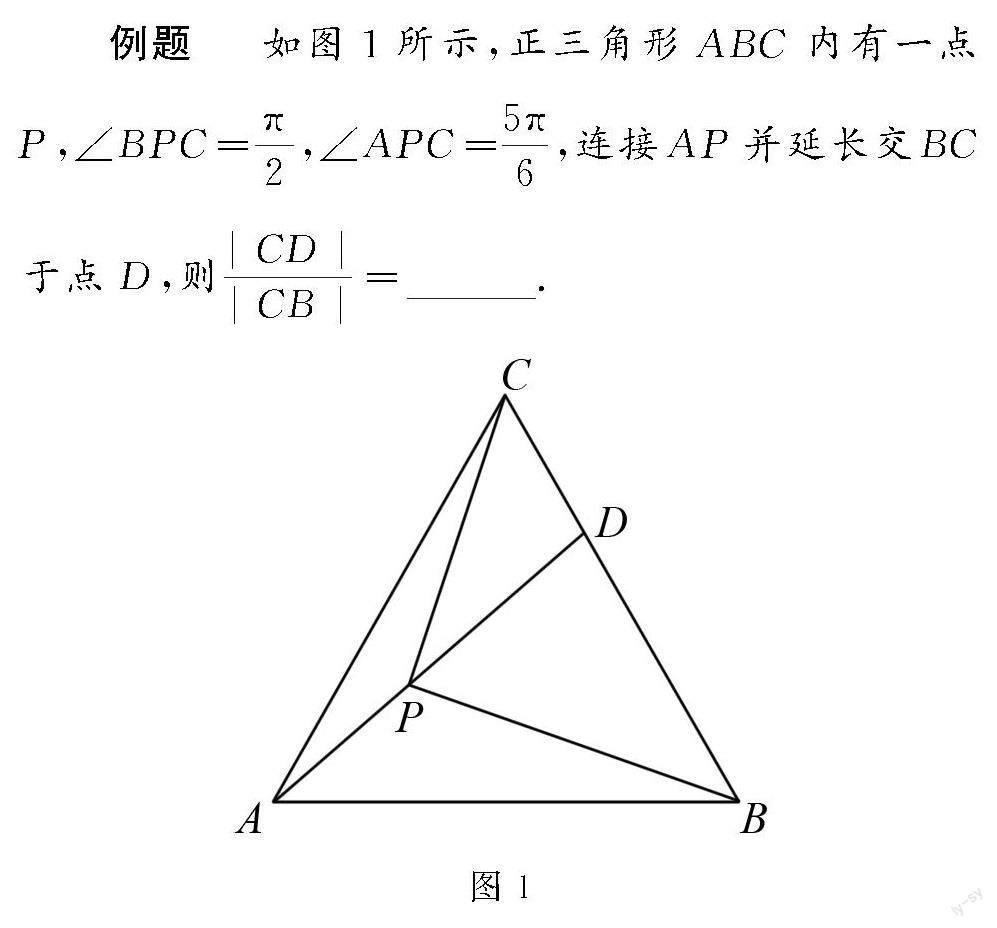
例题  如图1所示，正三角形ABC内有一点P，∠BPC=π2，∠APC=5π6，连接AP并延长交BC于点D，则|CD||CB|=.

图1

解析  本题以点的位置为基础，在正三角形这样的特殊三角形背景下研究长度比值问题，同时利用了“布洛卡点”这样的拓展情境，符合新高考对于题目创新的要求，具有很好的区分度.

方法1  有机转化边和角

解决三角形问题重点要关注三角形的边和角，就是利用题目中的条件将各种不同的三角形的边和角进行结合讨论.虽然是一个整体的题目，但是往往在研究时先聚焦于一个三角形，利用正、余弦定理，三角形面积公式等知识点进行运算，有时还会出现题目中的条件难以处理的情况，也可以另外设元，构造相关的等式来研究.

解  设正三角形ABC的边长为2，

|CD|=2λ，∠CDP=θ.

在△CAD中，∠CAD=2π3－θ，

由正弦定理可得|CD|sin2π3－θ=CAsinθ，

代入得λ=sin2π3－θsinθ.

在Rt△CPB中，可得

|CP|=|CB|cos∠BCP=2cos5π6－θ.

在△CDP中，由正弦定理可得|CD|sinπ6=|CP|sinθ，

代入可得λ=cos5π6－θ2sinθ.

由上述两式可得cos5π6－θ=2sin2π3－θ.

展开并整理可得tanθ=－33.

于是得到λ=sin（2π3－θ）sinθ=13.

所以|CD||CB|=2λ2=λ=13.

将角与边的关系经过合理的转化变为有用的条件代入到所需的表达式中后就需要合理运用设参的技巧，借助正、余弦定理，三角恒等式就可以得到基本的关系式，从而解出所需要的量.在运算过程中合理使用中间量也是解决此类问题的重要方法.

方法2  面积表示方法等价转化

面积表示方法等价转化的关键在于找到适合于面积转化的三角形，并且对于待求的量，要使其能够通过面积等式转化得出.所以在面积的表示形式上就会有所讲究，有时不仅需要代数运算，还需要从几何图形上观察出一些特征，从而达到简化过程的目的.

解  设∠CBP=θ，

则有∠ABP=π3－θ，

而∠APB=2π3，

则知∠PAB=θ.

在Rt△BPC中，

|PB|=|BC|cosθ，|PC|=|BC|sinθ.

在△APB中，有|PB|sinθ=|AB|sin2π3，

从而可得|PB|=233|AB|sinθ=|BC|cosθ，

又因为|AB|=|BC|，

所以tanθ=32.

所以|CD||DB|=S△PCDS△PDB=12|PC‖PD|sinπ612|PB‖PD|sinπ3

=|PC|sinπ6|PB|sinπ3=12|BC|sinθ32|BC|cosθ

=tanθ3=12.

因此根据|CD|，|CB|，|DB|三者的关系可得|CD||CB|=13.

此方法是解三角问题的常用方法，在发现同底或者等高的三角形时，就可以考虑在三角形之间建立相应的关系，再将其面积通过同一变量表示出来，解出相对应的特殊点，就可以得到答案.同时表示面积时还需要考虑用哪个角作为夹角来计算，也会在运算上起到作用.

方法3  运用正弦定理转化

正弦定理中最常见的形式就是比值，有时还需要将外接圆半径当做一个中间量来求解，但是往往不需要解出具体的数值，只需要解出表达式即可.在使用正弦定理时，也可以将其它三角形中的正弦定理形式写出，根据补角的正弦值相等的性质，也可以得到需要的条件.

解  设∠CBP=θ，

则有∠ABP=π3－θ，

而∠APB=2π3，

则知∠PAB=θ.

在Rt△BPC中，

|PB|=|BC|cosθ，|PC|=|BC|sinθ.

在△APB中，结合正弦定理有|PB|sinθ=|AB|sin2π3，

从而可得|PB|=233|AB|sinθ=|BC|cosθ，

又因为|AB|=|BC|，

所以tanθ=32.

在△ABD中，再次结合正弦定理可得

|BD|sinθ=|AB|sin2π3－θ.

然后由此式整理可得

|BD|=|AB|sinθsin2π3－θ=23|AB|

=23|BC|.

所以|CD||CB|=13.

对于长度比值问题，题目中的条件肯定会混杂着三角形的角和边两个方面，此时正弦定理就可以建立两者之间的桥梁.在直接用长度算比值难度较大的情况下，就可以尝试转化成角的形式进行比较，有时可能有意想不到的效果.

结语

以上三种方法从三角形之间的转化，面积的转变，正弦定理边角的互换三个方面解决了这道问题.在运算时合理采取数形结合的思想也能达到简化运算的目的.总的来说，解三角形问题是常用到数形结合思想的一类问题.充分利用三角形三角有关公式，将知识串联起来，问题就可迎刃而解.