例析相似三角形问题的常见模型及解题思路
朱长梅


【摘要】相似三角形是初中数学十分常见的一类问题,也是必须熟悉和掌握的数学内容.对相似三角形问题的图形进行分析并归类,大致可分为A字模型、旋转模型、8字模型等,学生掌握这些常见模型,能够加强对相似三角形的理解,也能在一定程度上提高解题的准确度.本文主要结合例题分析不同模型对应的图形特点和证明三角形相似的思路,帮助学生深刻理解,提高得分率.
【关键词】初中数学;相似三角形;解题技巧
1 旋转相似模型
旋转相似模型具体是指將一个三角形绕一个定点旋转并放大或缩小,得到对应图形,所得到的三角形被称为旋转相似三角形,且原三角形与旋转得到的三角形相似.根据这一模型特点,可以解答一类旋转相关的相似三角形问题,具体解题思路如下所示.
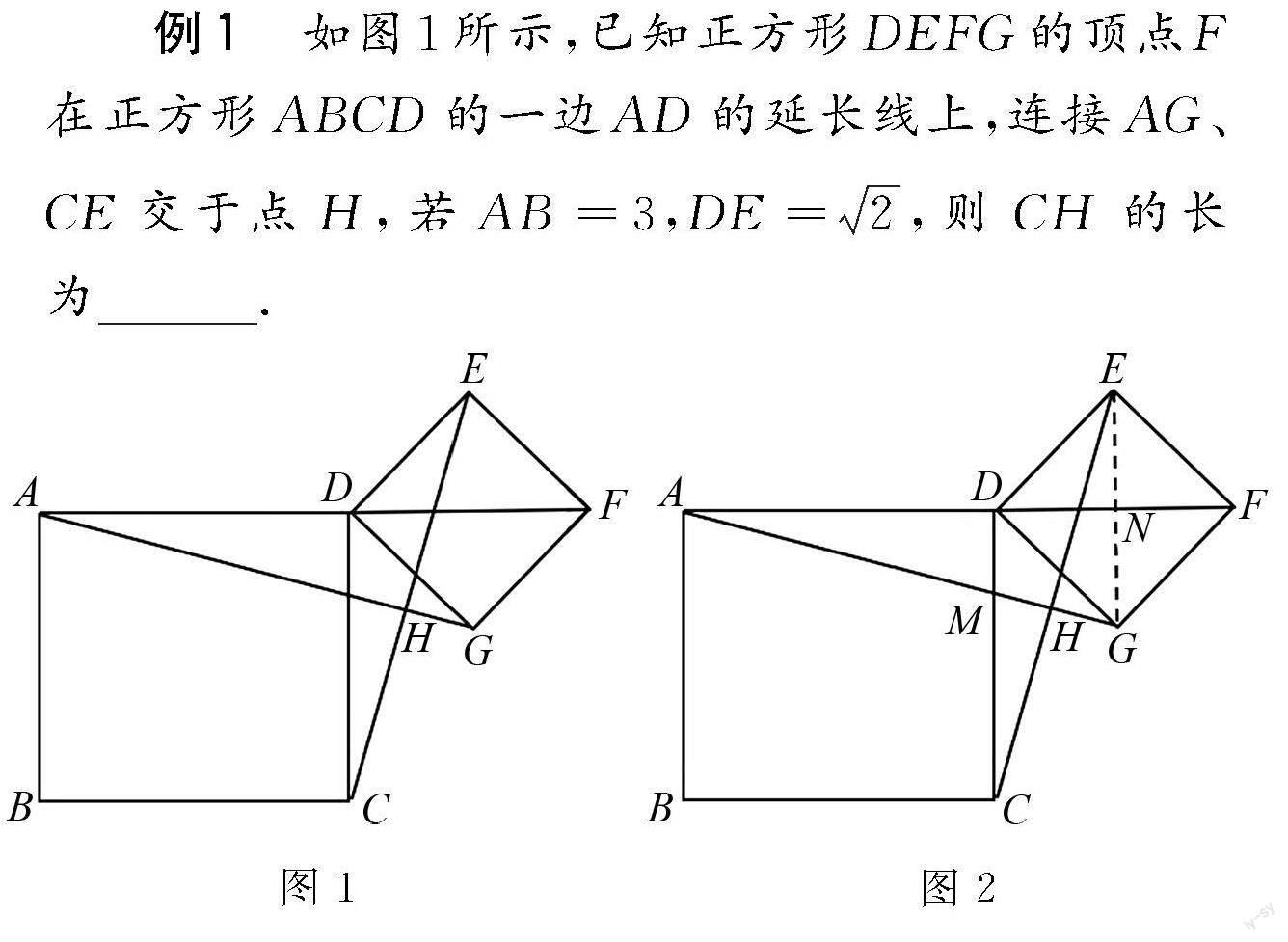
例1 如图1所示,已知正方形DEFG的顶点F在正方形ABCD的一边AD的延长线上,连接AG、CE交于点H,若AB=3,DE=2,则CH的长为.
分析 首先该题图形属于旋转相似模型,唯一不同是旋转的图形是正方形.需要找出相似的一组三角形并判别,根据相似边长比得到CH的长,即可对问题做出解答.
解析 如图2所示,连接EG,与DF交于点N,
设CD和AH交于点M,
所以∠GNA=90°,
DN=FN=EN=GN,
所以△ANG∽△ADM,
所以DMNG=ADAN,
因为DE=2,
所以DF=EG=2,DN=NG=1,
因为AD=AB=3,
所以DM1=33+1,
解得DM=34,
所以MC=94,
AM=AD2+DM2=3174,
因为∠ADM+∠MDG=∠EDG+∠CDG,
所以∠ADG=∠EDC,
在△ADG和△CDE中,AD=CD∠ADG=∠CDEDG=DE,
所以△ADG≌△CDESAS,
所以∠DAG=∠DCE,
因为∠AMD=∠CMH,
所以∠ADM=∠CMH=90°,
所以△ADM∽△CHM,
所以ADCH=AMCM,即3CH=317494,
解得CH=91717.
2 母子相似模型
母子相似模型具体是指两个相似三角形具有一条公共边和一个公共角的图形,图形特点主要是两三角形互相依靠,是十分常见的一类相似模型.掌握该模型有助于学生灵活解题,具体解题思路为:①根据已知条件和图形特点,找到相同比的一组三角形边长,②根据相似三角形判定依据,找到相似三角形,解答问题.
例2 如图3,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB边运动,速度为2m/s,点Q从点B开始沿BC边运动,速度为4m/s,如果P、Q两动点同时运动,何时△QBP与△ABC相似?
分析 该题图形为母子相似模型,解题时需要从结论出发找到符合题意的条件,即相似三角形的边长比,根据判别三角形的定理列出相关等式,解相关方程组即可求出具体答案.
解析 设经过ts时,△QBP与△ABC相似,由题意可得AP=2t,
BP=8-2t,BQ=4t,
因为∠PBQ=∠ABC,
当BPAB=BQBC时,△BPQ∽△BAC,
即8-2t8=4t16,
解得t=2s,
当BPBC=BQBA时,△BPQ∽△BCA,
即8-2t16=4t8,解得t=0.8s,
所以经过2秒或经过0.8秒时,△QBP与△ABC相似.
3 8字相似模型
8字相似模型具体是指图形交叉特点形似“8”字,且通常认为对顶角所对应的一对三角形相似.判别8字相似模型中的相似三角形,需要具备平行边,即对顶角所对的边平行,即可找到一组相似的三角形.具体解题思路和特点如下例题所示.
例3 如图4,在平行四边形ABCD中,E是边长AD的中点,连接AC、BE交于点F,若△AEF面积为2,则△ABC的面积为( )
(A)8. (B)10. (C)12. (D)14.
分析 首先要找出△AEF和△ABC之间的联系,△AEF和△ABC图形与“8”字模型十分相似,故可按照8字相似模型解题.根据相似三角形判别定理判断相似,其次根据边长比得到对应面积比,即可得知具体面积值.
解析 因为四边形ABCD是平行四边形,
所以AD∥BC,AD=BC,
因为点E是边长AD的中点,
所以BC=2AE,
因为AE∥BC,
所以∠EAC=∠BCA,
因为∠EFA=∠BFC,
所以△AEF∽△CBF,
如图5所示,过点F做FH⊥AD于点H,FG⊥BC于点G,
则EFBF=AFCF=AEBC=HFFG=12,
所以S△AEFS△ABC=12AE·FH12BC·HG=12BC·FHBC·3HG=16,
因为S△AEF=2,
所以S△ABC=6S△AEF=12.
4 结语
灵活应用并判别相似三角形模型,是学生在学习过程中需要掌握的内容.上述例题分别对不同相似模型做出分析和应用,各种模型都有各自的图形特点,在解题中应引起学生的重视.掌握基础知识和判别三角形相似的定理,是解答相似三角形的基础,也是学生必须掌握的内容.
参考文献:
[1]江田.相似三角形中的探索型问题例析[J].语数外学习(初中版),2020(04):24-25.
[2]陆志才.相似三角形探索题例析[J].中学生数理化(初中版),2006(Z1):26-29.

