微振动模拟与主被动隔振一体化实验平台

秦 超，周洪海，贺 帅，徐振邦*，朱 赫

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.中国科学院 空间光学系统在轨制造与集成系统重点实验室，吉林 长春 130033）

1 引言

随着遥感应用市场的扩大，对遥感卫星图像分辨率和像质的要求越来越高［1］。高稳定性是高分辨率的基础，而遥感卫星中反作用飞轮组件（Reaction Wheel Assembly，RWA）、控制力矩陀螺仪（Control Moment Gyroscope，CMG）和制冷机产生的微振动是影响稳定性的主要原因［2-3］。这些微振动具有振幅小、频带宽的特点，不会使结构破坏，但通过卫星结构传递到光学系统会导致遥感卫星的图像质量显著降低［4］。因此，需要预测在轨微振动对光学有效载荷性能的影响。

模拟空间微振动环境，在地面进行微振动实验是验证航天遥感器能否在轨可靠工作的重要措施［5］。在高分辨率成像科学实验（HiRISE）项目中，对指向稳定性误差进行了分配，RWA 的结构非理想对称性产生的振动干扰被认为是最严重的影响因素，其次是制冷机和框架驱动器［6-7］。RWA 的主要扰动频率在0～200 Hz［8］，CMG 和制冷机产生的微振动频率为60～300 Hz［9-11］。因此，在进行微振动实验时，实验系统在这些频段要有效模拟在轨真实情况。

遥感卫星的地面微振动实验有两个重要要求：一是要隔离除仪器本身微振动源以外的其他扰动；二是为仪器提供能够模拟其真实工作时的微振动环境，以光学仪器载荷与卫星平台安装接口为界面进行模拟。Park 等开发并测试了针对RWA 的单轴微振动模拟器［12］，Zheng 等设计了六自由度微振动激励平台，可满足同时进行多频激励的要求且在300 Hz 的频率内可以达到较高的控制精度［13］，但模拟实验时两者均未考虑外界扰动的隔离。为隔离外界扰动，Chao 等设计了一种被动隔振系统，将空间望远镜的LOS 衰减率降至48%，并使像点位置更加集中，有效地减少了微振源对空间望远镜的影响［14］。Beijen 等设计了一种主被动隔振系统，实现了74%～97%的隔振效果，均方根调平误差降至1/8［15］。但尚无公开文献报道能够同时实现微振动模拟和采用主被动措施隔离外界扰动的微振动实验平台。因此，本文将隔离外界扰动的主被动隔振系统与微振动模拟器相结合，提出了一种集微振动模拟和主被动隔振为一体的多功能实验平台。根据实验需求对实验平台各部组件进行了合理布局，并通过有限元分析验证了设计的正确性。为了抑制被动隔振系统共振峰处的放大，引入主动隔振系统，通过主动阻尼力降低共振峰振幅［16］。此外，通过基于线性叠加系统的频响函数控制方法实现了工作台面的微振动模拟，从仿真和实验两个层面证明了微振动模拟的准确性。

2 结构设计

2.1 构型设计

实验平台如图1 所示，由大理石平台、4 个气浮支撑、8 个音圈电机以及结构支撑件组成。大理石平台尺寸为1 800 mm×2 000 mm×350 mm，自身质量为4×103kg，可承受负载质量为8×103kg。气浮系统的工作原理是高压气体充入橡胶囊中，通过气压的作用将工作平台浮起，此时气浮台在平动和转动方向有6 个自由度。同时，气囊将工作平台与结构支撑分离构成系统的被动隔振单元。安装在工作平台和基础框架之间X，Y，Z向的音圈电机为主动执行机构，可对工作平台施加多维主动力来实现主动隔振与微振动模拟。

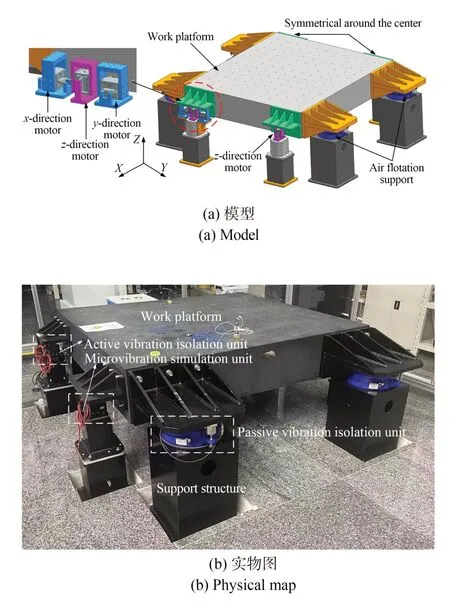
图1 微振动模拟与主被动隔振一体实验平台示意图Fig.1 Schematic diagram of integrated experimental platform for micro-vibration simulation and active-passive vibration isolation

2.2 实验平台的模态分析

实验平台的有限元模型如图2 所示，模态分析结果如表1 和图3 所示。从表1 中可以看出，实验平台的前六阶模态均小于10 Hz，满足设计和使用要求。

表1 一体化实验平台的模态分布Tab.1 Modals of integrated experimental platform

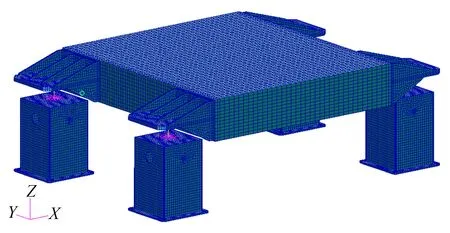
图2 实验平台的有限元模型Fig.2 Finite element model of experimental platform

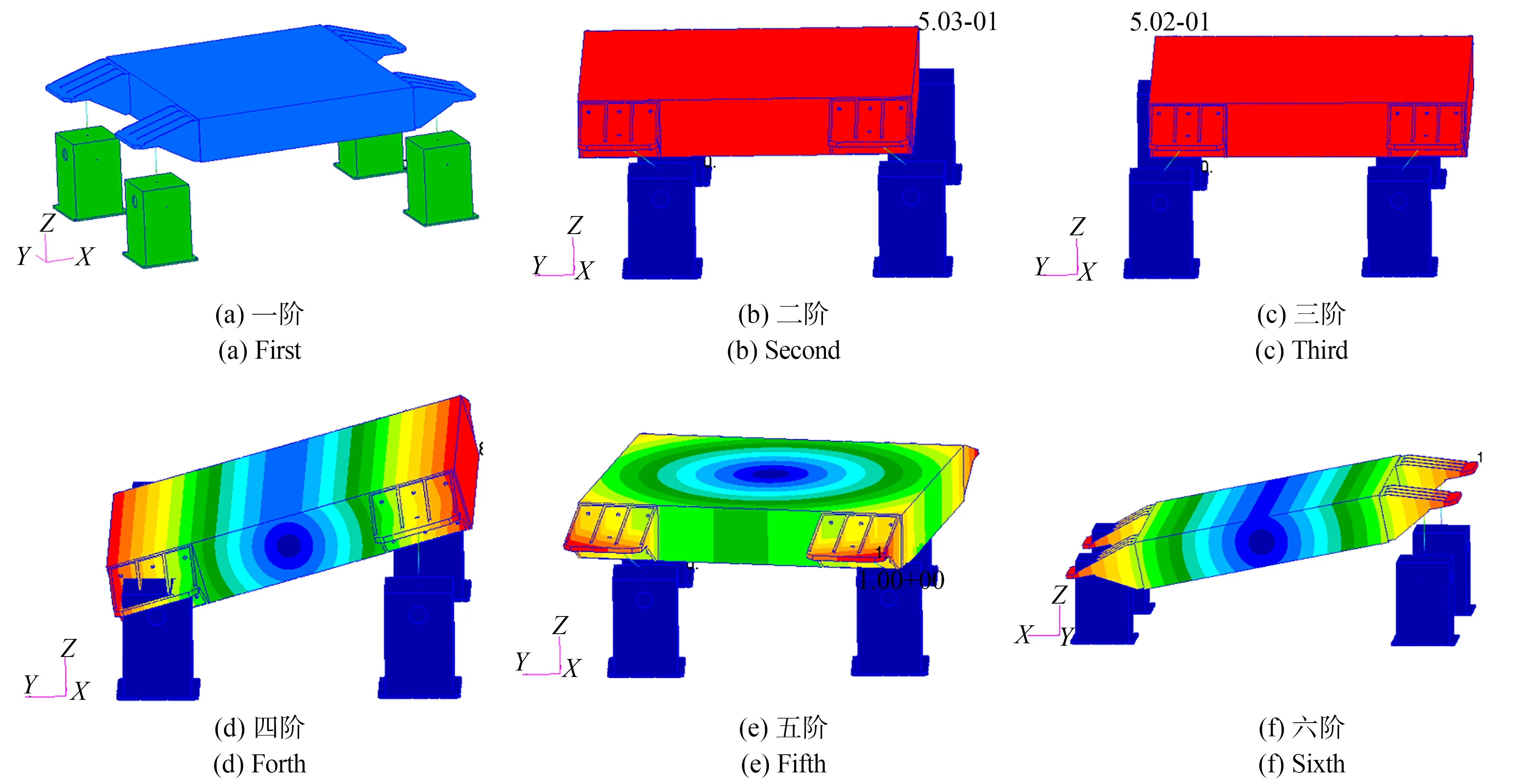
图3 一体化实验平台的前六阶模态Fig.3 First sixth modals of integrated experimental platform

3 隔振特性

3.1 被动隔振特性

被动隔振系统由结构支撑、气浮装置和工作平台组成。高压气体充入气浮装置的橡胶囊中形成气腔，它具有较大的负载支撑能力，同时利用空气的可压缩性形成隔振系统的刚度，为隔振系统提供较低的结构固有频率，改善高频隔振性能。被动隔振系统的原理如图4 所示。系统的振动微分方程为：

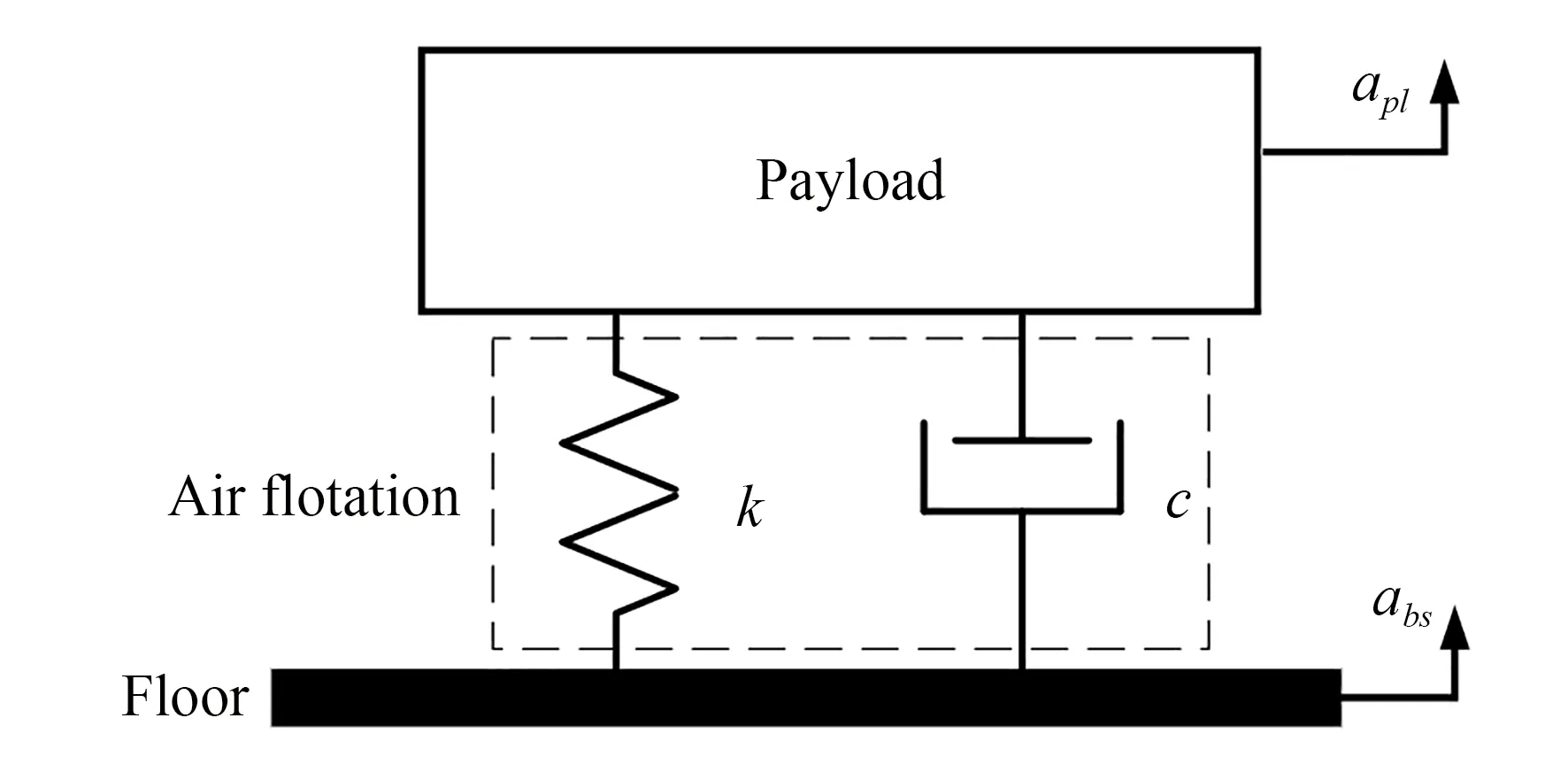
图4 气浮被动隔振原理Fig.4 Principle for air-floating passive vibration isolation

其中：M为质量矩阵，C为阻尼矩阵，K刚度矩阵，z(t)为地面位移扰动。对式（1）进行拉式变换（初值为0）后得：

对于稳态振动，令s=jω可得：

其中：ω为响应频率；H(ω)为地面扰动至工作平台响应的频率响应函数，用来显示被动隔振效果。

图5 为被动隔振系统开启后，当输入为地面扰动时，大理石台面的隔振效果。可见相比于无被动隔振系统，高频振动衰减明显。在10～100 Hz 频段内，空气弹簧支撑的隔振效果要明显优于刚性连接系统；而对于口径较大的光学载荷，主镜、次镜支撑桁架等关键组件的固有频率均在此频段内，由此说明了设计的有效性。

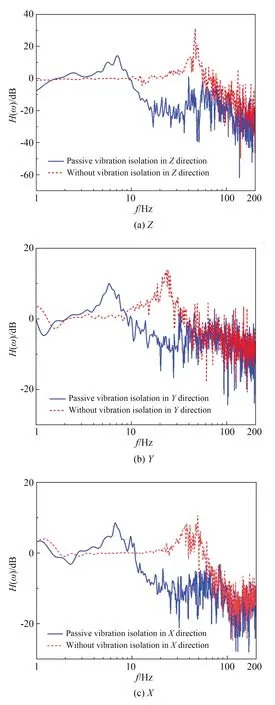
图5 不同方向的被动隔振效果Fig.5 Effect of passive vibration isolation in different directions

3.2 主动隔振特性

被动隔振系统能够有效地衰减远高于隔振系统固有频率的高频扰动，但代价是在隔振系统固有频率处会对输入的振动进行放大。为了克服这一问题，可以采用主动阻尼控制策略对隔振系统共振峰进行抑制，具体方法为直接速度反馈和正加速度反馈。

反馈控制原理如图6 所示，其中k，c和m是系统刚度、阻尼系数和质量。apl和abs分别为负载加速度和地面环境输入加速度，apl作为反馈信号输入至执行机构，执行机构为音圈电机（持续推力为50 N，峰值推力为150 N，力常数为10.1 N/A）产生主动作用力fac抑制负载的振动。系统控制回路如图7 所示。

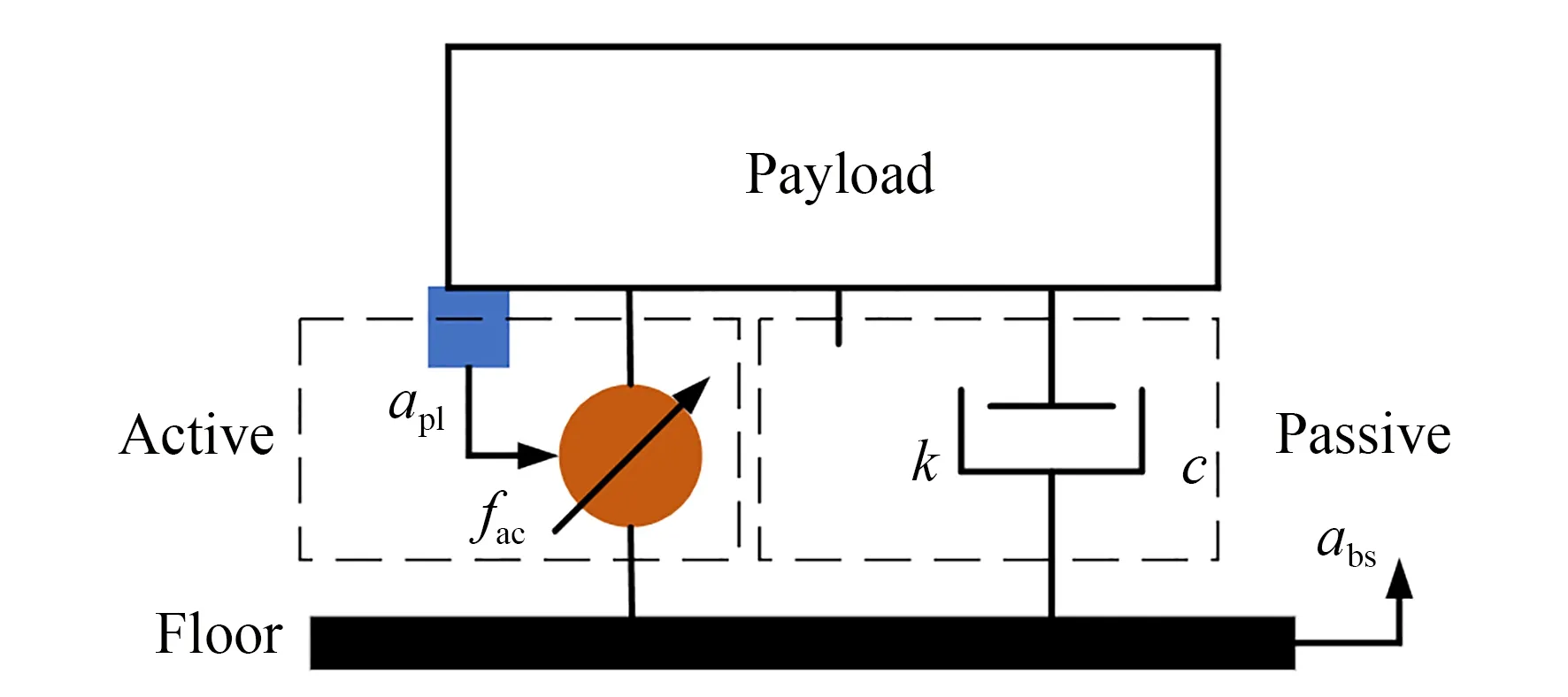
图6 基于反馈的主动隔振原理Fig.6 Principle of active vibration isolation based on feedback

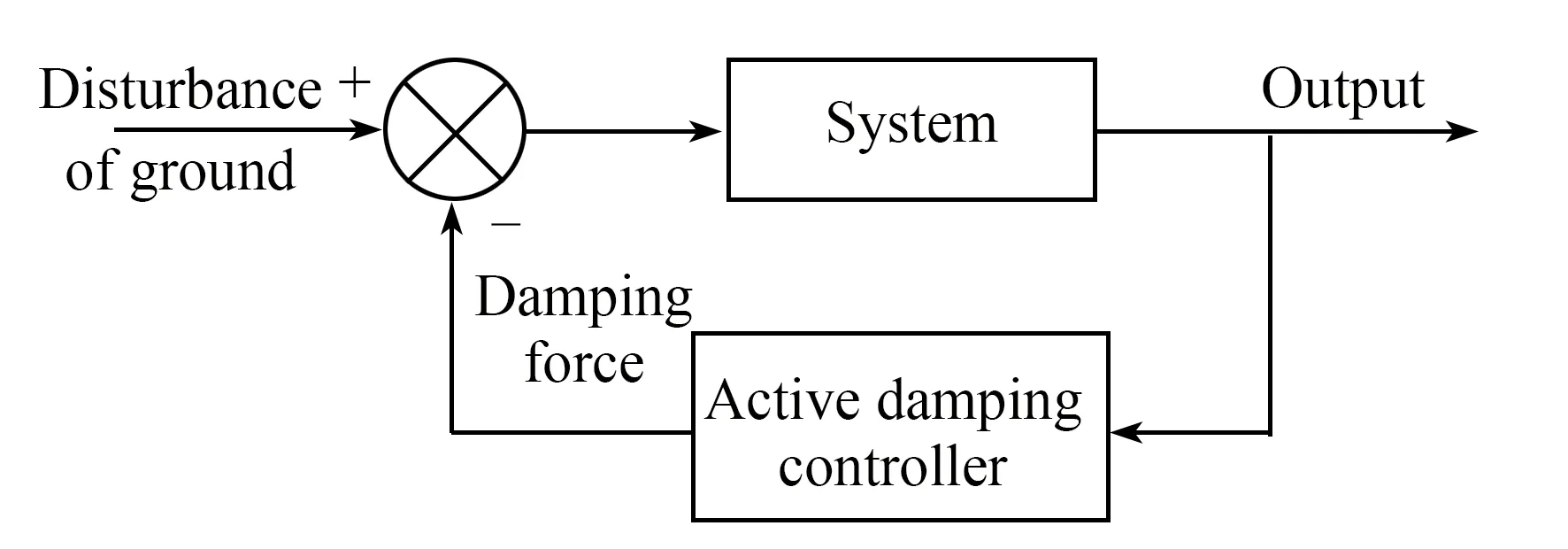
图7 主动阻尼控制回路Fig.7 Active damping control loop

直接速度反馈形式简单，同位控制（反馈测量和控制力加载为同一位置）控制器的输出信号仅为：

其中：g为控制增益，X(s)为反馈点位移的拉式变换，u(s)为控制器输出信号的拉式变换。该控制策略在使用时要根据实际情况配置滤波器。

另一种控制策略为正加速度反馈，该方法为正位置反馈的变形，其控制为：

对上述主动阻尼控制策略进行了实验验证，整个电控测试系统如图8 所示，控制器采用倍福CX9020-0115。输入激励为地面扰动，测试得到的主动隔振效果如图9 所示。与被动隔振状态相比，被动隔振系统引入导致的振峰群幅值明显减小，Z向的最高峰值由22 dB 下降至8 dB。由此说明，主动隔振效果良好，验证了主动阻尼控制策略的有效性。

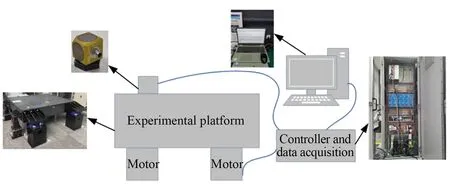
图8 电控测试系统Fig.8 Electronic control system

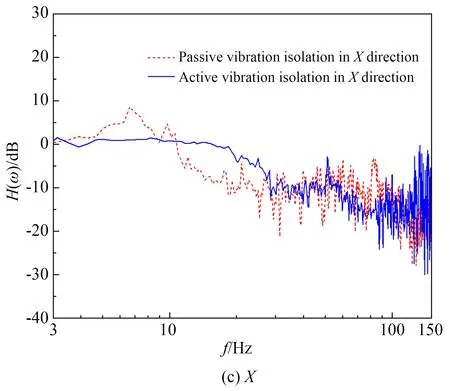
图9 不同方向的主动隔振效果Fig.9 Effect of active vibration isolation in different directions

4 微振动模拟

微振动模拟的理论基础为基于线性叠加系统的频响函数控制策略。采用这种方法的优势是不依赖于主动力的分布形式以及无需建立详细的被控系统数学模型。一般情况下，微振动模拟的扰动形式为单频或多频线谱，也就是电机输出力为谐波形式，设单频扰动输入为：

其中fi为单个电机输出力幅值，相应的加速度响应为：

其中ai为加速度响应幅值。

假设系统阻尼为小量级比例阻尼，在这种谐波输入力下，系统的稳态响应可以写为频响函数与输入力在频域上的乘积，即：

通过实验依次令f1到f8为单位1，读取加速度响应向量的值，利用式（9）即可得到频响函数矩阵。在得到频响函数矩阵后，如果目标加速度为A，则所需的控制力向量为：

其中Hg为频响函数矩阵的广义逆。

目前，常见的商用加速度传感器只能测量线加速度［17-18］。因此，为了实现台面的角加速度测量和控制，需要对加速度传感器进行如图10 所示的形式布局。

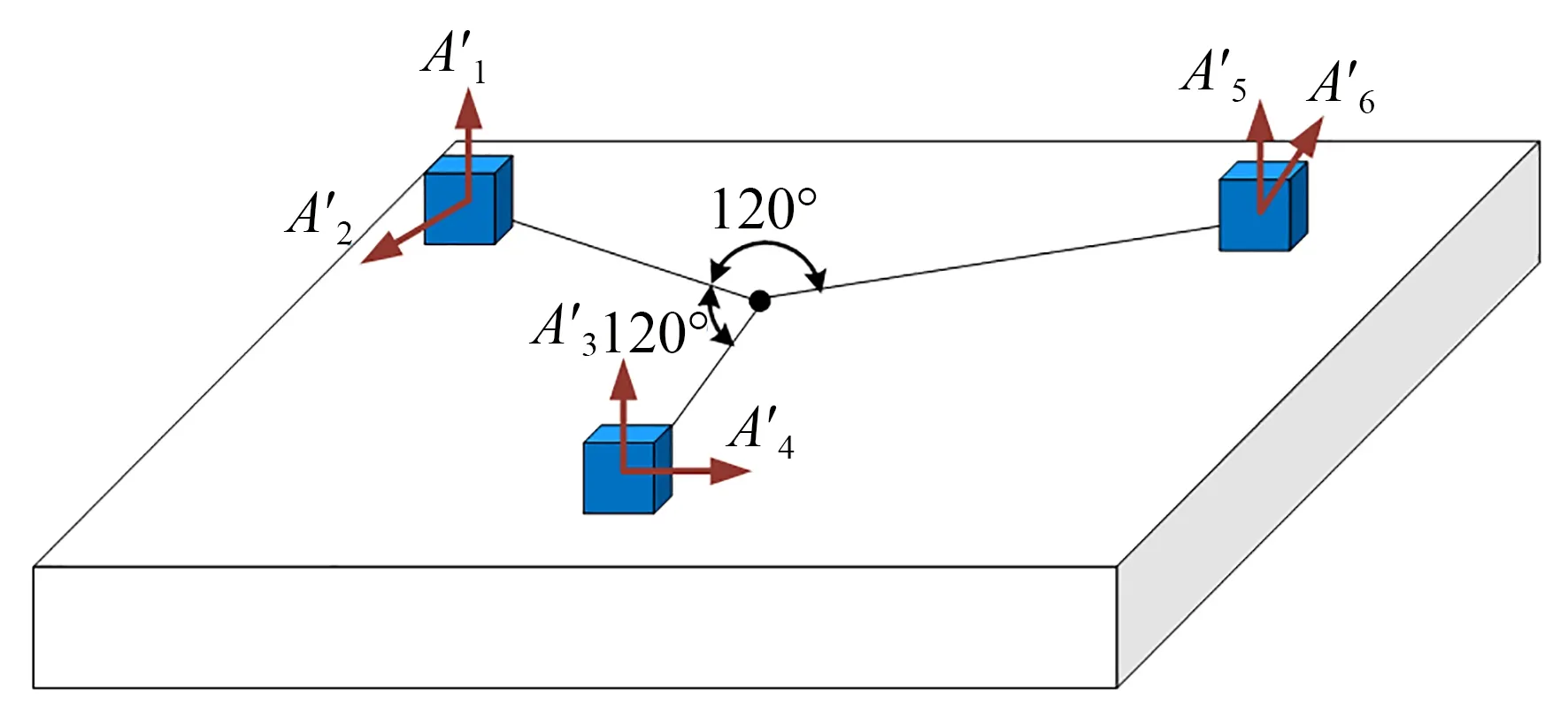
图10 微振动模拟测量传感器分布Fig.10 Distribution of sensors in micro-vibration simulated measurement

3 个三向传感器在半径为R的圆上呈120°分布，3 个传感器的Z向分别为分量A1′，A3′，A5′，与圆周相切的位移分量分别为A2′，A4′，A6′。考虑到响应为微振动，高阶量可以忽略，由这6 个加速度分量合成中心点的加速度，得到：

设定目标中心加速度后，再通过求解方程组（11）得到对应的3 个传感器的6 个分量，对这6 个分量进行控制，即能实现预设的加速度目标。

采用有限元方法对该控制策略进行仿真验证，设定目标加速度为［1，1，1，0.001，0.001，0.001］T，平动加速度单位为mm/s2，转动加速度单位为rad/s2，频率为85 Hz。为展示效果，截取1～1.2 s的模拟效果曲线与目标值进行对比，如图11 所示，模拟曲线与目标曲线吻合度良好。

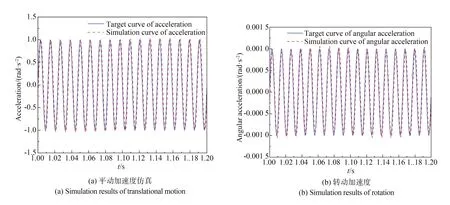
图11 单频谐波模拟时域仿真验证Fig.11 Time domain simulation results of single frequency harmonic

通过仿真验证算法后，对微振动模拟效果进行实测，电控测试系统如图8 所示。首先是单频工况，X，Y和Z轴方向的目标平动加速度模拟量为50 Hz-0.7 mg，目标转动加速度模拟量为50 Hz-60 mrad/s2。实验结果如图12 所示，误差统计见表2，最大误差为3.22%，误差量小于10%。

表2 单频加速度模拟效果测试结果Tab.2 Test results of single frequency harmonic simulation

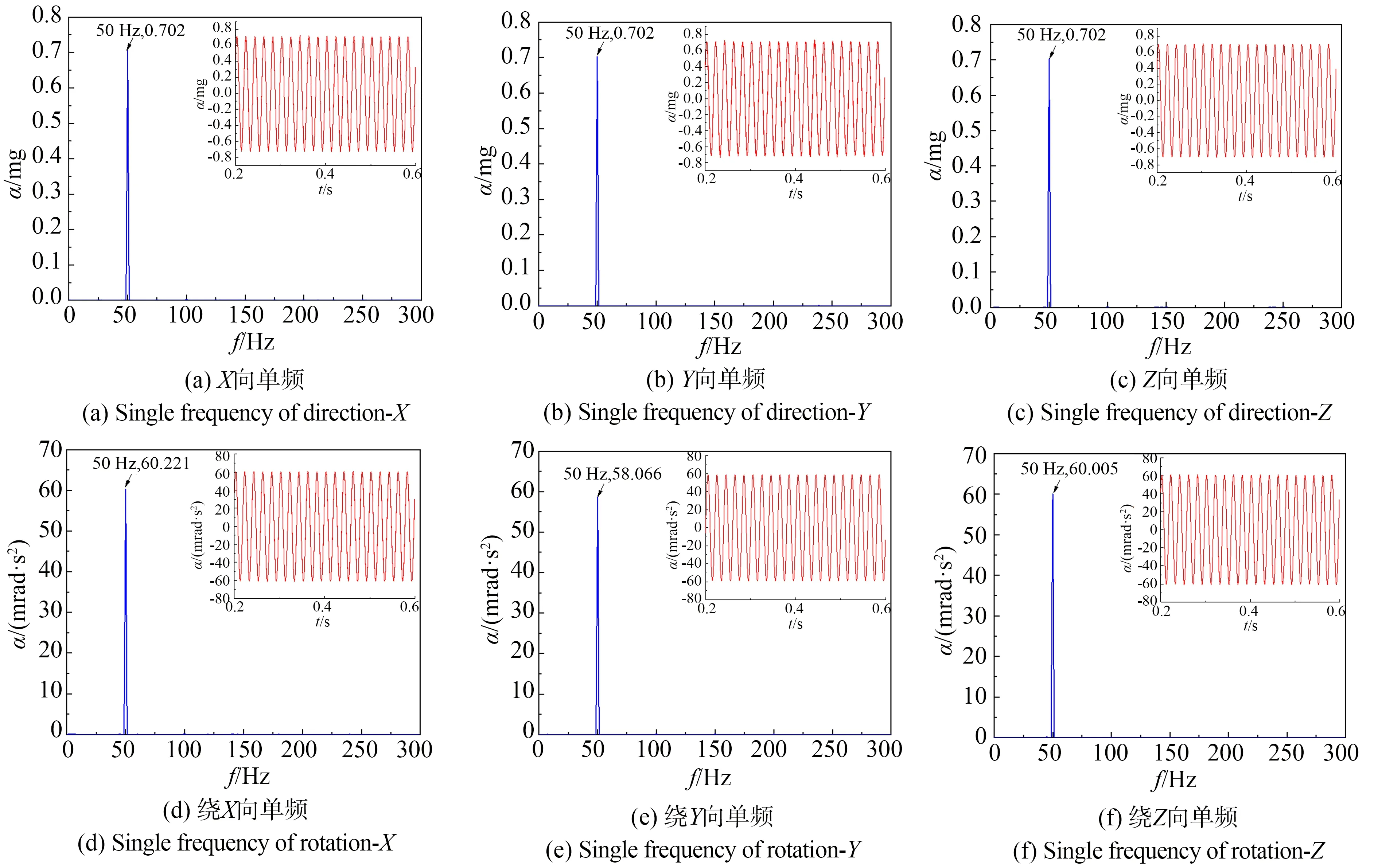
图12 实测台面单频线谱模拟效果Fig.12 Test results of single frequency harmonic simulation

RWA 等主要卫星平台扰动源在实际工作时输出的扰动形式为多频线谱，频率多集中在10～200 Hz，这就要求本实验平台可以同时输出多个特定频率的扰动。实验选取3 个频率组合的目标模拟加速度，在X，Y和Z轴方向的目标平动加速度模拟量分别为20 Hz-70 mg，50 Hz-70 mg，100 Hz-70 mg，目标转动加速度模拟量分别为20 Hz-60 mrad/s2，50 Hz-60 mrad/s2，50 Hz-60 mrad/s2。实验结果如图13 所示，误差统计见表3，最大误差为5.90%，误差量小于10%。实验结果表明：该模拟器可以很好地模拟RWA 等典型卫星平台扰动源的扰动特性。

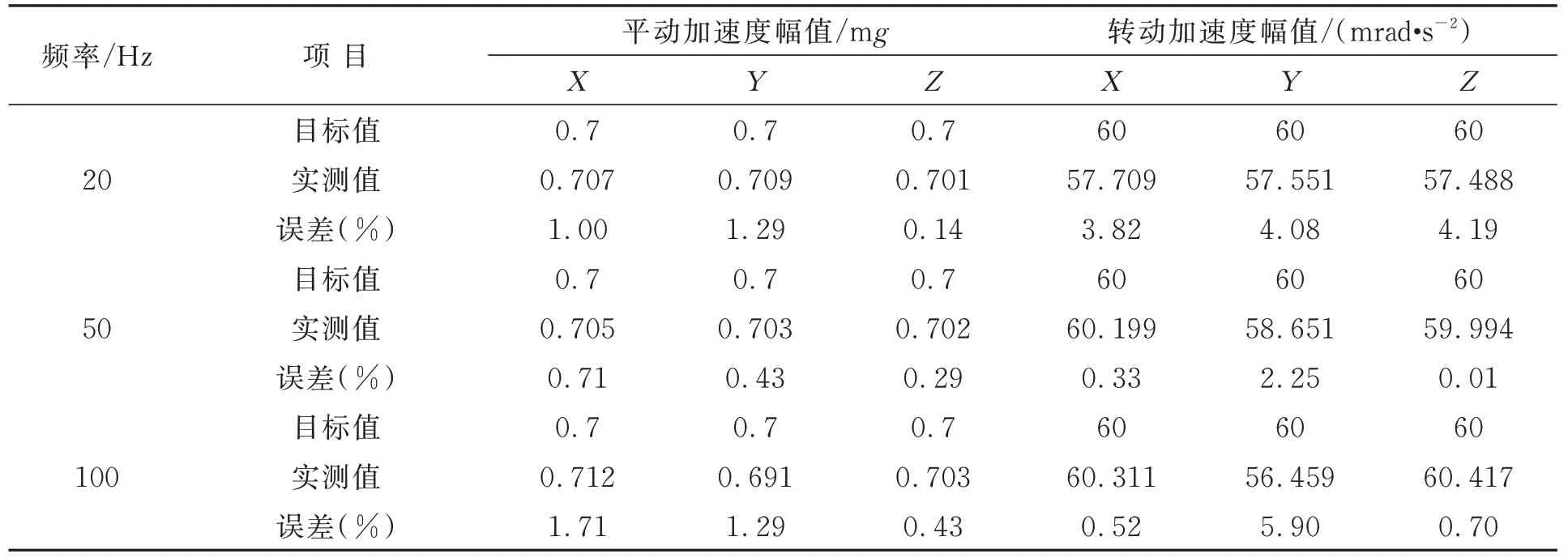
表3 多频加速度模拟效果测试结果Tab.3 Test results of multifrequency harmonic simulation

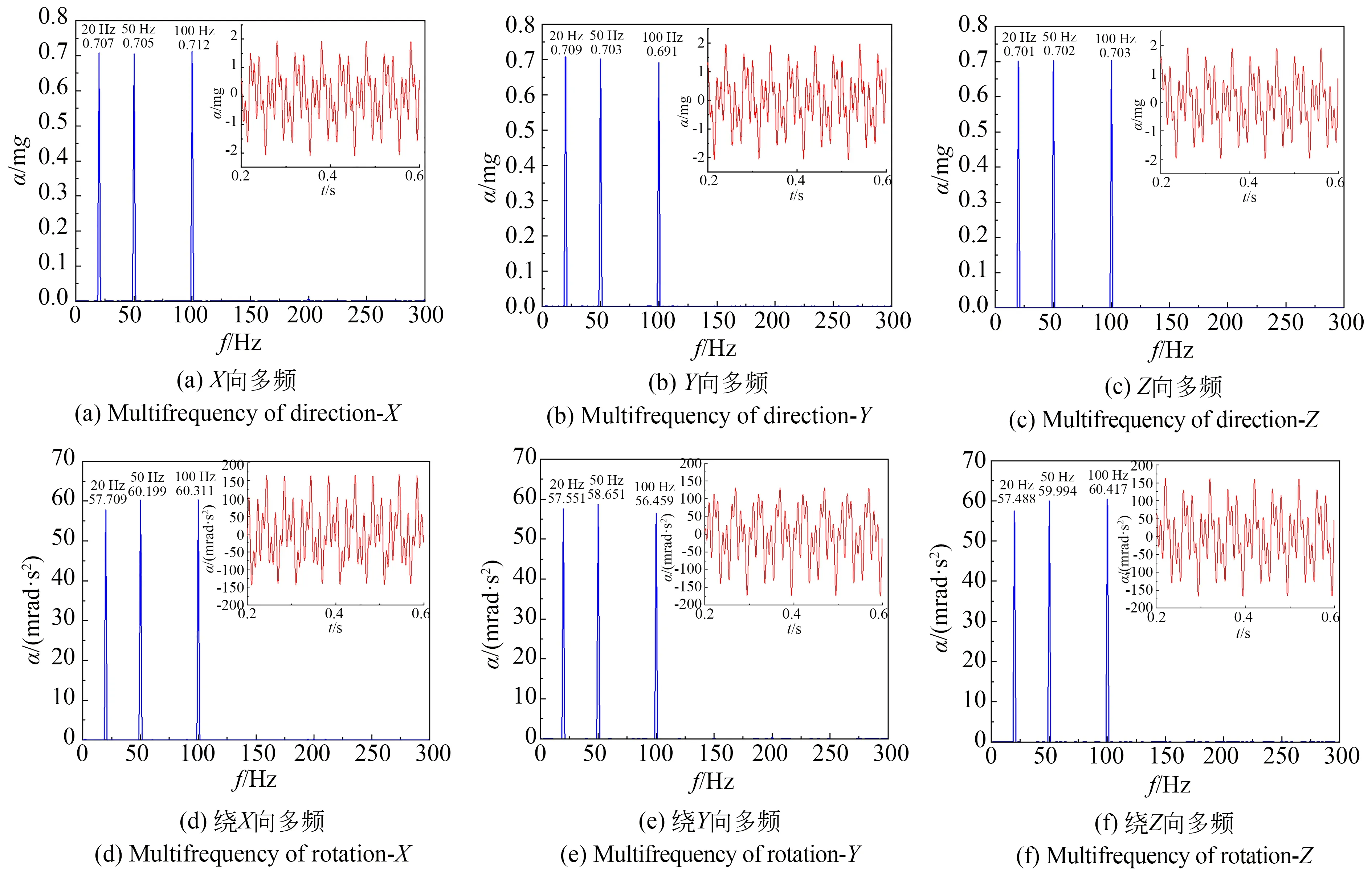
图13 实测台面多频线谱模拟效果Fig.13 Test results of multifrequency harmonic simulation

5 结论

为了满足遥感卫星地面微振动实验的复杂要求，本文设计了一种微振动模拟器与主被动隔振平台复合的一体化实验平台。该平台可承受5×103kg 的载荷，前六阶的模态频率分布均小于10 Hz，被动隔振系统能大幅抑制10～200 Hz 以内的地面微振动，能够提供小于1 μg 的微振动环境。主动隔振能够实现14 dB 的隔振系统共振峰衰减效果，同时进一步提高平台在低频段的隔振能力。微振动模拟功能能够有效模拟遥感卫星RWA 和制冷机等主要扰动源的单频和多频微振动线谱，在特定频谱的扰动实验中，加速度幅值的最大误差仅为5.9%。实验结果表明，该一体化微振动实验平台的各项功能均能满足实验需求。