光学遥感卫星精密敏捷成像控制技术综述

曲友阳，钟 兴，戴 路，范林东，徐 开

（1.长光卫星技术股份有限公司，吉林 长春 130102；2.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；3.中国科学院大学，北京 100049）

1 引言

随着航天遥感技术的飞速发展，光学遥感卫星的空间分辨率、时间分辨率和光谱分辨率不断提高［1］，成像功能逐渐多元化、灵巧化，不再局限于传统的推扫成像功能，还扩展出单星同轨立体成像［2］、多目标多条带成像［3-4］和灵巧沿迹成像［5］等功能。与此同时，光学遥感卫星成像能力的提升也对其姿态控制系统的性能提出了更高的要求，超稳定、超精确、超敏捷的精密敏捷控制是高分辨率光学遥感卫星实现多功能、高质量成像的重点技术。

高分辨率光学相机对卫星的姿态控制精度有着极高的要求。对于成像空间分辨率为0.5～1 m，轨道高度约为500～700 km 的光学遥感卫星，其姿态确定精度要达到0.002 7°，姿态指向精度和姿态稳定度要达到0.03°和0.001（°）/s。高分2 号卫星［6］的空间分辨率为0.81 m，姿态确定精度优于0.003°，姿态指向精度优于0.05°，姿态稳定度优于5.0×10-4（°）/s。世界先进的光学遥感卫星WorldView-4［7］的空间分辨率为0.46 m，姿态确定精度优于8.3×10-5°，姿态指向精度优于2.8×10-4°，姿态稳定度优于1.0×10-4（°）/s。此外，为了实现同轨立体成像、多目标多条带成像功能，以及快速响应的应急成像任务，光学遥感卫星应具备敏捷姿态机动能力，以实现不同姿态间的快速调节。吉林一号高分02卫星［8］基于星载一体化设计技术，利用反作用飞轮（Reaction Wheel，RW）作为执行机构结合敏捷机动控制算法，可在40 s 内机动25°。Pleiades-1卫星［9］利用力矩输出能力更强的控制力矩陀螺（Control Moment Gyro，CMG）作为执行机构，姿态机动60°仅需25 s。

高分辨率光学遥感卫星的成像能力与其姿态控制系统的性能息息相关，复杂成像功能的实现多受限于卫星的姿态机动能力，高质量的成像则被卫星的姿态确定与控制精度制约。在实际工程中，快速、准确、稳定的姿态控制是高分辨率光学遥感卫星设计的首要目标之一。然而，光学遥感卫星姿态控制系统面临着复杂的物理约束［10-11］，执行机构的输出力矩和响应速度约束限制了姿态机动能力，传感器的测量精度约束限制了姿态确定精度，卫星模型参数的精度约束则会影响姿态控制的精度。另一方面，由于空间环境因素，卫星在轨运行过程中存在非受控的外部力矩，包括重力梯度力矩、剩磁力矩、气动力矩和太阳光压力矩［12-13］。此外，卫星姿态机动过程中也可能引发太阳帆板等挠性部件的振动，从而产生扰振力矩［14-15］。虽然这些干扰力矩量级较小，但对于无重力环境下的卫星姿态运动来说，仍会影响其姿态指向精度和姿态稳定度。总体而言，光学遥感卫星超稳定、超精确、超敏捷姿态控制系统的实现面临诸多挑战，需要综合考虑成像系统需求、姿态控制系统配置和策略进行设计，利用先进的技术方法，在满足成像系统基本需求的前提下，充分挖掘控制系统的能力。

本文对光学遥感卫星精密敏捷成像控制技术进行了系统性的分析与研究。首先，说明了超稳定、超精确、超敏捷的姿态控制性能对光学遥感卫星成像的意义。接着，介绍了卫星姿态控制系统的组成和原理，以此为基础论述了每个部分的关键技术和最近进展。最后，结合当前光学遥感卫星的发展趋势和工程需求，对光学遥感卫星一体化成像控制技术的发展给出了建议。

2 姿态控制性能与卫星成像

2.1 姿态机动能力与多功能成像

姿态敏捷机动能力对光学遥感卫星实现多功能成像至关重要，卫星的姿态机动能力越强，多功能成像模式获取的遥感图像范围越大，质量越高。

2.1.1 多目标连续成像

多目标连续成像模式是在同一轨道周期内，通过连续调节卫星的侧摆角度，对观测范围内的多个目标点进行连续推扫成像［16］，以提高光学遥感卫星的时间分辨率和观测覆盖率。但是，多目标成像模式非常依赖卫星的姿态机动能力［17］，以三目标点连续成像为例，多目标连续成像模式示意图如图1 所示。图中有3 个期望的推扫成像目标点，当完成对目标点A的推扫成像后，卫星必须在规定的时间TBtrans内快速调节姿态使得光学相机指向目标点B，否将错过对目标点B的观测窗口。总之，卫星的姿态机动能力越强，在固定的卫星运行时间Torbit内可进行观测的目标点就越多，获取的成像数据越丰富。

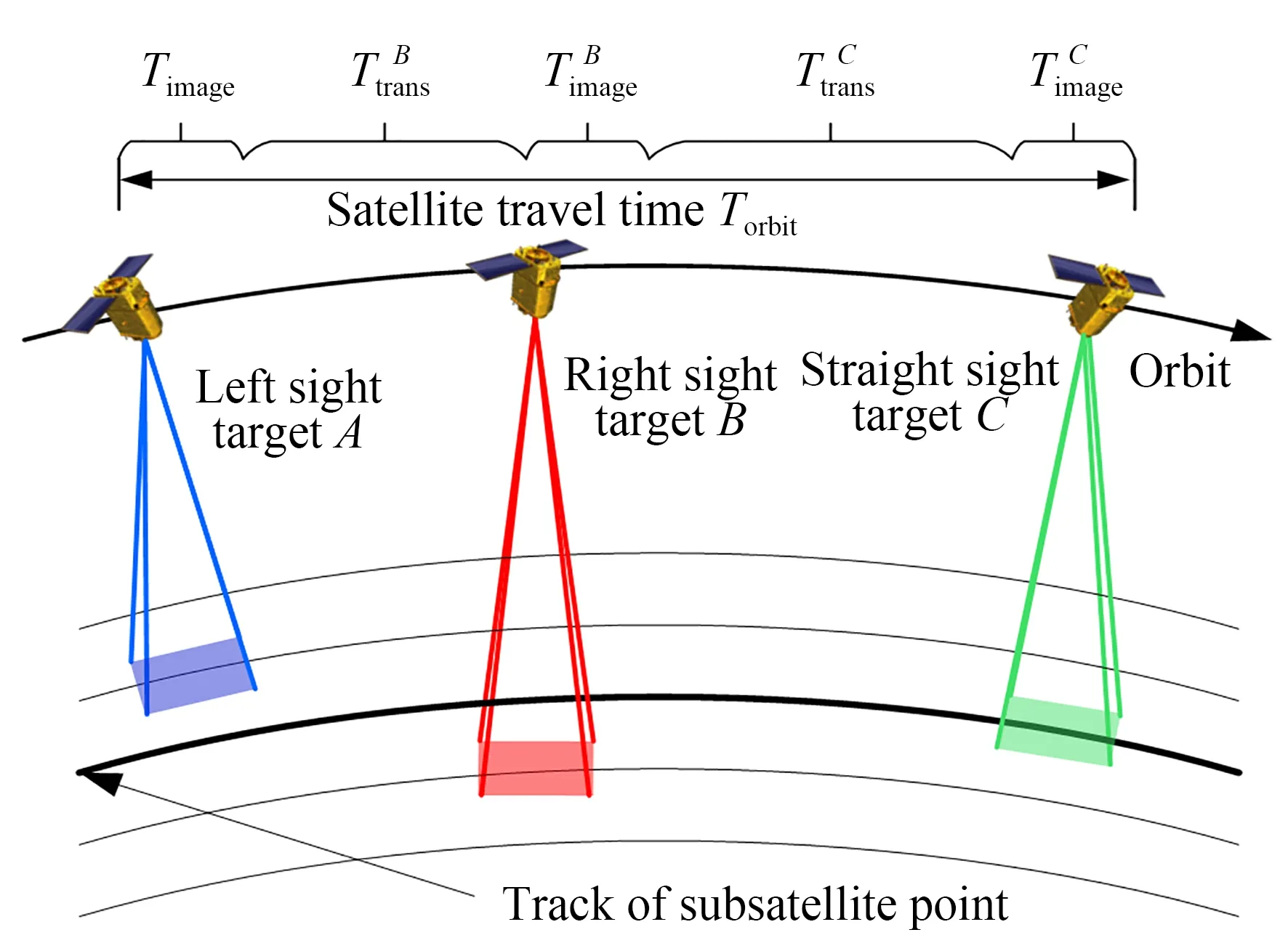
图1 多目标连续成像模式示意图Fig.1 Schematic diagram of continuous multi-point imaging

2.1.2 同轨立体成像

光学遥感卫星通过两次以上对同一地面目标进行不同角度的观测成像，结合地面图像处理可以获取目标点的三维影像［18］。以双视立体成像为例，同轨立体成像模式示意图如图2 所示。图2 说明了利用单个光学相机，通过卫星俯仰轴姿态的快速机动实现同轨立体成像的基本原理。同轨立体成像缩短了立体像对的获取时间间隔，影像环境差异小，成像效率高［2］，已成为获取立体遥感图像的重要手段。

图2 同轨立体成像模式示意图Fig.2 Schematic diagram of stereo imaging on same orbit

同轨立体成像模式下，卫星的成像过程分为前视与后视两部分，其成像的时间关系为：

其中：Timage为前视和后视推扫成像的时间；Ttrans为卫星的姿态机动时间。卫星的姿态机动能力越强，Ttrans越短，则Timage越长，获取的立体成像区域越广。

2.1.3 多条带成像

光学遥感卫星在白天降轨成像时，星下点轨迹自北向南。高分辨率光学遥感卫星的幅宽一般为15～50 km，对于东西跨度大、南北跨度小的成像目标点，单次成像任务无法实现区域覆盖，需要通过多次拍摄和拼接才可完成区域的覆盖成像任务。针对这一问题，卫星可通过快速的三轴姿态机动，连续对同一目标点进行多条带成像，最后拼接成一幅数倍于单次推扫成像幅宽的遥感影像［4］。以三条带成像为例，图3 给出了多条带成像模式示意图，其姿态机动过程综合了多目标连续成像和同轨立体成像，需要同时进行连续侧摆和俯仰姿态机动，以对目标点进行前视左摆、正视和后视右摆成像，最终获取三倍于卫星成像幅宽的遥感影像。三条带成像的时间关系为：

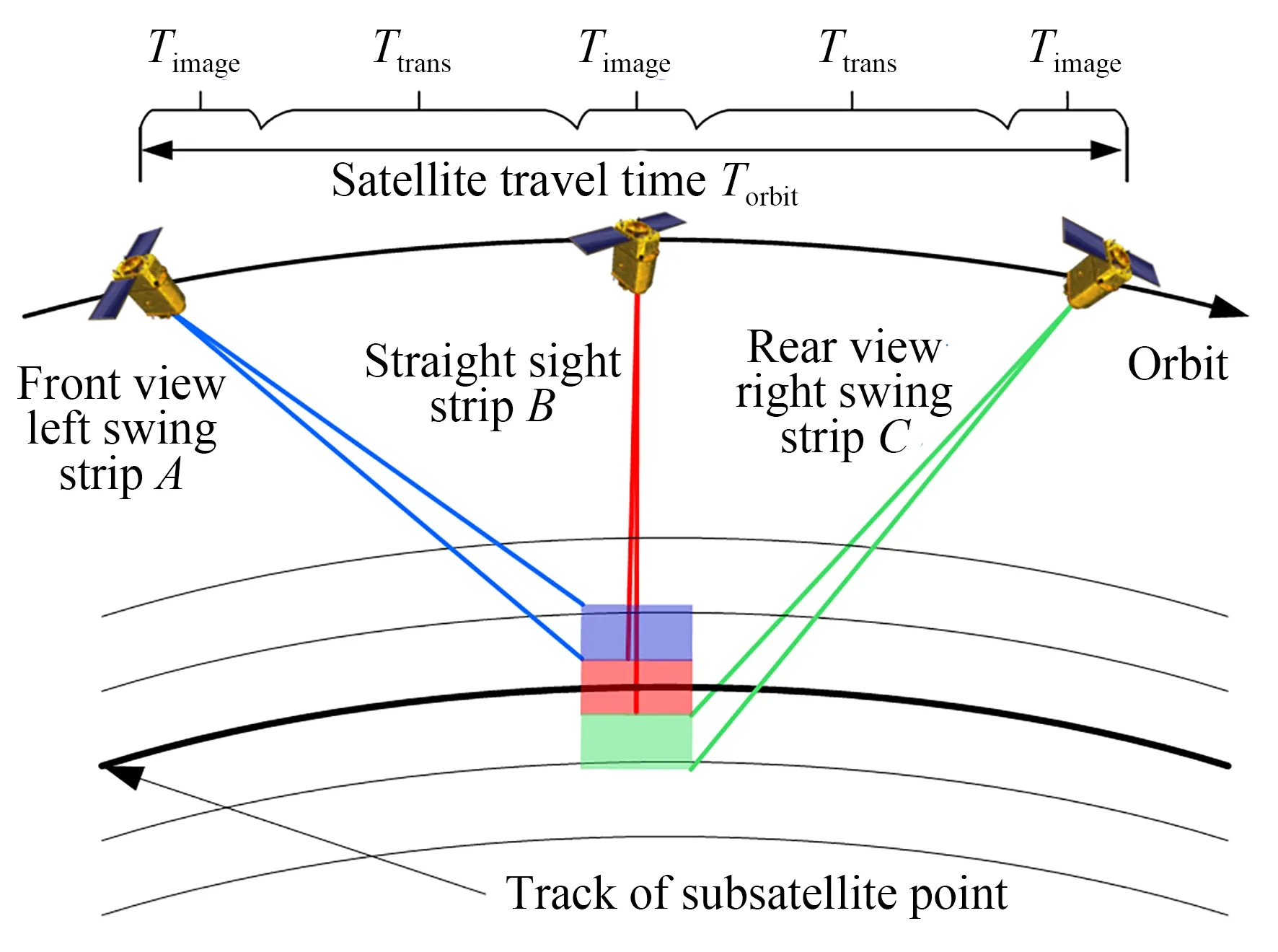
图3 多条带成像模式示意图Fig.3 Schematic diagram of multi-strip imaging

根据上述关系，姿态机动时间Ttrans应小于Torbit/2，否则卫星不具备多条带成像的能力。在此基础上，卫星的姿态机动时间越短，单个条带的推扫成像时间越长，成像区域越大。

2.2 姿态确定精度与成像质量

高分辨率光学遥感卫星在轨获取的图像数据通过数传任务传输至地面，此后需利用卫星的姿态信息将图像数据拼接生产得到遥感图像，因此，卫星平台的姿态确定精度决定了遥感图像的几何精度［19］。姿态确定误差分为系统误差和随机误差。系统误差主要是由星敏感器的光行差、安装矩阵标定误差和热变形误差组成，对于这类误差，可以利用光行差修正和在轨标定的方法进行补偿。随机误差主要是由星敏感器和陀螺仪的测量噪声组成，是姿态测量误差的主要因素。

根据姿态确定误差与图像几何定位精度的数学模型［20］，结合吉林一号高分04 星的参数，分析了姿态确定误差对图像几何定位精度的影响，结果如图4 所示。如图4（a）所示，图像几何精度同时受俯仰角误差和成像时俯仰角的影响。当俯仰角为0°，俯仰角误差为1″时，图像沿轨方向的几何定位误差为2.6 m；俯仰角误差为5″时，图像沿轨方向的几何定位误差为13.0 m。若俯仰角增大到30°，5″俯仰角误差对应的几何定位误差增大到17.3 m。总体而言，俯仰角误差是影响图像沿轨方向几何定位精度的主要因素，基础俯仰角起到误差放大的作用，即俯仰角越大，相同俯仰角误差导致的图像几何定位误差越大。图4（b）描述了滚转角误差对图像垂轨方向几何精度的影响，其规律与图4（a）相似。

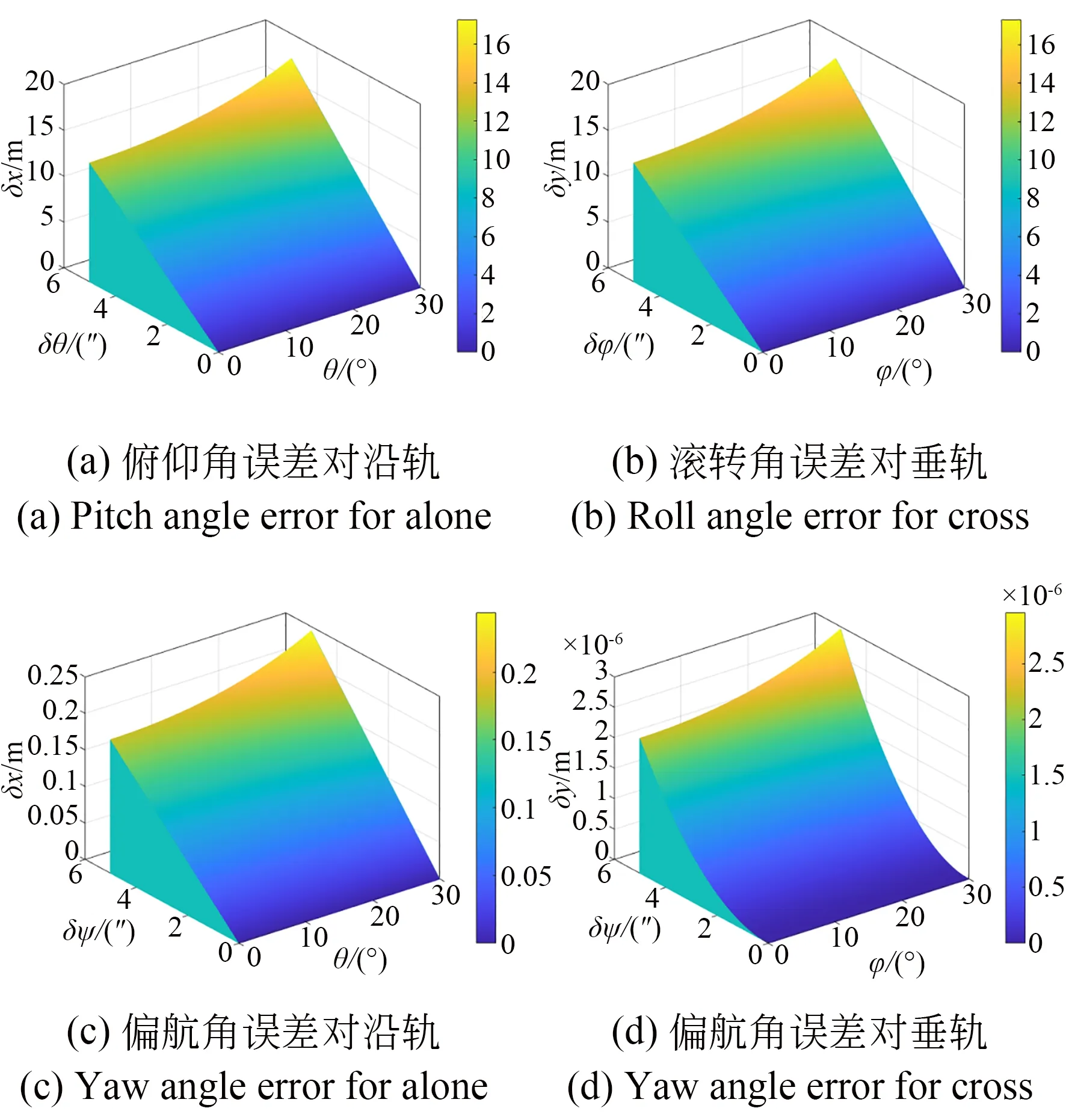
图4 姿态确定误差对图像几何精度的影响Fig.4 Influence of attitude determination errors on geometric positioning accuracy of image

偏航角误差对图像沿轨方向和垂轨方向几何精度的影响分别如图4（c）和图4（d）所示。当偏航角误差为1″，俯仰角为0°时，图像沿轨方向的几何定位误差为0.037 m；当偏航角误差增加到5″时，图像沿轨方向的几何定位误差为0.18 m。偏航角误差导致图像垂轨方向的几何定位误差均小于10-5m。总体而言，偏航角误差远小于俯仰角误差和滚转角误差对图像几何定位精度的影响，尤其是对图像垂轨方向几何精度的影响可以忽略不计。

2.3 姿态控制精度与成像质量

光学遥感卫星的成像质量可以利用调制传递函数（Modulation Transfer Function，MTF）来评估。高分辨率光学遥感卫星通常采用时间延迟积分成像的电荷耦合元件（Time Delay and Integration Charge-Coupled Device，TDICCD）设计光学载荷，其成像的MTF 受多方面因素的影响，包含光学设计、电子探测器、姿态指向误差、姿态稳定度误差和轨道高度变化等［21］。

在轨成像期间，卫星的姿态控制误差会导致TDICCD 的电荷积累运动与地面轨迹在焦平面上的投影运动产生差异，使得卫星地面轨迹速度在相机焦平面上的投影，即像移速度与TDICCD的行转移速度不一致；或是TDICCD 电荷的积累方向与图像运动方向的夹角，即偏流角控制不准确，进而致使临近的目标影像混叠，引起运动模糊，最终导致成像质量下降［22-24］。因此，姿态指向误差和姿态稳定度误差对高分辨率光学遥感卫星的成像质量尤为重要，与卫星沿轨和垂轨方向的成像质量息息相关［22，25］，直接决定了光学成像系统的动态MTF。

为了定量说明姿态控制精度对成像质量的影响，根据姿态控制误差与成像MTF 的数学模型［22］，评估了姿态指向误差和姿态稳定度误差对光学遥感卫星图像质量的影响。依次设置三轴姿态指向误差为0.1°，0.2°和0.5°，计算对应的相移速度误差ΔV和偏流角误差Δβ，则卫星在垂轨和沿轨方向成像的MTF 分别为：

其中：MTFct，MTFat分别为垂轨和沿轨方向的成像MTF 值；N为TDI 成像的积分级数；f/fN为光学系统的归一化频率；V为卫星的飞行速度。

姿态指向误差对图像MTF 影响的分析结果如图5 所示。从图中可以观察到，滚转角误差和俯仰角误差对图像的MTF 基本没有影响；当偏航角误差为0.1°，0.2°和0.5°时，图像垂轨方向奈奎斯特频率点的MTF 分别为0.998 5，0.954 8，0.737 3，偏航角误差导致图像垂轨方向的MTF严重衰减。这是由于偏航角的控制误差直接对应成像的偏流角误差，当偏流角误差过大时，势必会导致成像模糊，图像的MTF 下降。

图5 姿态指向误差对图像MTF 的影响Fig.5 Influence of attitude pointing errors on MTF of image

同理，依次设置卫星三轴姿态角速度误差为0.001（°）/s，0.003（°）/s 和0.01（°）/s，同姿态指向误差分析的方法一样，分别计算不同角速度误差情况下的相移速度误差和偏流角误差，并根据相移速度误差和偏流角误差计算卫星成像的MTF，得出姿态稳定度误差对图像MTF 的影响，结果如图6 所示。从图中可以观察到，滚转角速度误差会严重影响垂轨方向的图像质量，当滚转角速度误差为0.003（°）/s 时，图像垂轨方向奈奎斯特频率点的MTF 衰减为0.934 8；当滚转角速度误差增大到0.01（°）/s 时，MTF 衰减为0.420 1。俯仰角速度误差则严重影响沿轨方向的图像质量，当俯仰角速度误差为0.003（°）/s时，图像沿轨方向奈奎斯特频率点的MTF 衰减为 0.934 3；当俯仰角速度误差增大到0.01（°）/s 时，MTF 衰减为0.418 0。此外，不同偏航角速度误差条件下，垂轨和沿轨方向的图像MTF 几乎不存在衰减，即偏航角速度误差对图像质量没有明显的影响。

图6 姿态稳定度误差对图像MTF 的影响Fig.6 Influence of attitude stability errors on MTF of image

总体而言，为了保证高质量成像，卫星姿态控制系统需要着重关注偏航轴的姿态指向精度，滚转和俯仰轴的姿态稳定度。对于滚转和俯仰通道，可以设置较低的控制带宽，加强对随机噪声的抑制作用，提高这两个通道的姿态稳定度；而偏航通道可以设置较高的控制带宽，加强系统的跟踪控制能力和干扰抑制能力，提高姿态指向精度。

2.4 小 结

光学遥感卫星的成像控制需要关注姿态控制系统多个维度的控制指标，卫星的成像能力和成像质量与控制系统的姿态机动能力、姿态确定精度、姿态控制精度交叉耦合。考虑到各项控制指标之间存在一定的制约关系，在控制系统的设计过程中，需要与卫星的成像需求紧密结合，分清各控制系统指标对卫星成像的重要性。在此基础上，充分利用先进的精密敏捷姿态控制技术，兼顾姿态控制的敏捷性与精密性，确保多功能、高质量的卫星成像。

3 精密敏捷姿态控制

光学遥感卫星的姿态机动能力、姿态确定精度和姿态控制精度（姿态指向精度和姿态稳定度）是实现高质量、多功能多模式成像的基石。如图7 所示，光学遥感卫星的姿态控制系统主要由四部分组成，包括精密敏捷姿态控制模块（姿态确定单元，姿态规划单元，姿态控制单元）、执行机构、姿态动力学和姿态传感器（星敏感器，磁强计，太阳敏感器，陀螺仪）。姿态动力学表征了实际卫星的姿态运动规律，是精密敏捷姿态控制模块设计的基础。姿态传感器测量卫星的姿态信息，通过姿态确定单元实现姿态四元数和姿态角速度的最优估计，并实时反馈给姿态控制单元。姿态控制单元根据姿态确定单元的反馈信息和姿态规划单元的规划信息，通过姿态控制算法生成控制信号发送给执行机构。最终，执行机构根据控制指令输出对应的控制力矩，控制卫星沿着预定的姿态轨迹指向期望姿态。

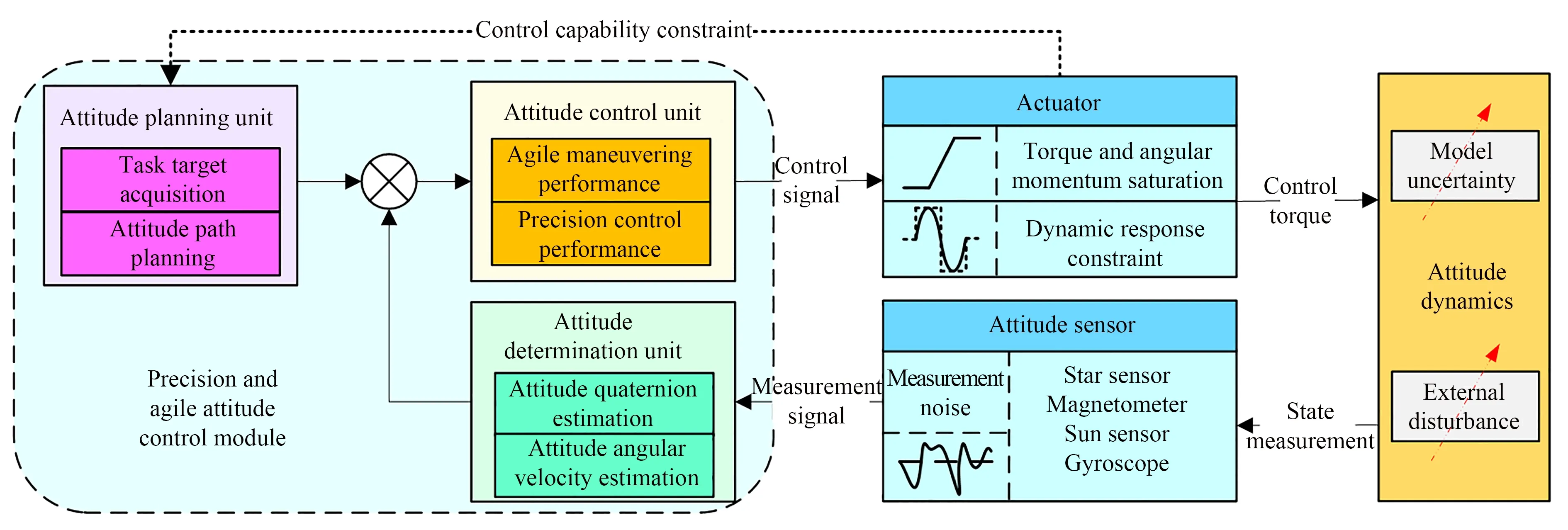
图7 卫星姿态控制系统结构Fig.7 Structure of satellite attitude control system

从图7 中可以观察到，卫星姿态控制系统中面临着各类问题：姿态传感器的测量信息包含噪声，执行机构的输出力矩和力矩响应速度存在约束，姿态动力学存在模型不确定性和外部扰动。这些问题限制了卫星的姿态机动能力，影响了卫星的姿态确定与控制精度，为高可靠、高精度、快机动的精密敏捷姿态控制技术实现带来了巨大的挑战。总体而言，在姿态传感器和执行机构已经确定的前提下，光学遥感卫星姿态控制系统的精密性取决于姿态确定单元和姿态控制单元；敏捷性取决于姿态规划单元和姿态控制单元。

3.1 精密姿态确定技术

高精度姿态确定信息在光学遥感卫星的姿态控制、任务执行和图像解析中起着重要的作用。精密姿态确定技术可以分为三大类［26］：第一类为静态姿态确定方法，利用代数方法和姿态传感器信息直接进行姿态解算，得到旋转变换矩阵或姿态四元数；第二类方法为动态姿态确定方法，根据卫星的姿态动力学，以姿态传感器的测量信息为观测值，利用卡尔曼滤波器或其他最优状态估计方法得到姿态的最优估计值；第三类方法为复合姿态确定方法，是前两类姿态确定方法的融合，将静态姿态确定的信息作为观测值，利用卡尔曼滤波器对姿态信息进行最优估计，以实现更高精度的姿态确定。

3.1.1 静态姿态确定方法

星敏感器、磁强计和太阳敏感器等确定性姿态信息均存在一定的缺陷，如磁强计、太阳敏感器仅能获取空间的单个姿态矢量信息，在解算卫星三轴姿态时存在奇异点，而星敏感器的光轴相比另外两轴精度较差。通过静态姿态确定方法将多个姿态矢量信息融合，能够弥补单独使用上述传感器的缺陷。TRIAD 方法［27］是一种利用两个矢量测量信息确定三轴姿态的静态姿态确定方法，如利用磁强计、太阳敏感器测量卫星本体坐标系下的磁矢量和太阳矢量，可以确定中等精度的姿态信息［28］，实现可靠的对日定向姿态确定；利用两个正交的星敏感器测量卫星本体坐标系下相互垂直的单位矢量，可以确定高精度的三轴姿态信息，有效克服了星敏感器光轴姿态精度低的问题。

然而，TRIAD 方法无法融合姿态向量中的全部信息，仅能实现次优的姿态确定［29］。此外，该方法仅能利用两个姿态矢量确定姿态，即使存在多个姿态矢量也无法实现更高精度的姿态确定。Wahba 问题［30］的提出实现了两个以上姿态测量矢量的加权解算，以确定最优的静态姿态。这类姿态确定方法总体可以分为两类，确定姿态四元数的四元数估计（Quaternion Estimator，QUEST）方法［31］，确定姿态矩阵的奇异值分解（Singular Value Decomposition，SVD）方法［32］和快速最优姿态矩阵（Fast Optimal Attitude Matrix，FOAM）方法［33］，广泛应用于多维姿态矢量的加权求解，实现了高精度的静态姿态确定。

3.1.2 动态姿态确定方法

动态姿态确定方法根据最优状态估计理论，利用卫星的姿态动力学进行状态预测，以传感器的测量信息进行观测修正，估计得到的姿态信息精度远高于静态姿态确定方法。文献［34］利用卫星姿态运动学模型建立了姿态确定的过程模型，根据姿态旋转变换矩阵建立了向量形式的观测方程，结合粒子滤波器实现了快速收敛的高精度姿态估计。文献［35］利用卫星的姿态运动学模型和陀螺的测量模型，建立了非线性姿态确定方程，结合扩展卡尔曼滤波器实现了中高精度的姿态确定，并准确估计了陀螺的零偏。上述两种方法分别采用姿态旋转矩阵和四元数直接作为状态变量建立状态方程，系统的非线度较高，难以兼顾运算效率和姿态确定精度。

误差四元数形式的姿态确定模型［36］线性化误差小，运行效率高。通过求解误差四元数形式的微分方程，结合卡尔曼滤波器可以实现低复杂度、高精度的姿态确定。这类利用误差四元数的方法统称为乘型扩展卡尔曼滤波器（Multiply Extended Kalman Filter，MEKF）姿态确定方法［37-38］，已被广泛应用于卫星的姿态确定与控制系统设计。针对使用星敏感器和陀螺仪的典型卫星姿态确定系统，文献［39］利用MEKF 方法对卫星的姿态四元数和角速度进行了高精度估计，并分析了线性化误差与姿态确定精度的关系，指出星敏感器的采样频率是影响模型线性化误差的主要因素。文献［40］提出了一种同时估计姿态状态和传感器测量误差的MEKF 方法，在对地三轴稳定模式下，利用星载重力梯度仪和陀螺仪实现了角秒级的姿态确定精度。此外，针对使用低成本MEMS 陀螺仪的小型卫星，文献［41］在经典MEKF 方法的基础上，将卫星的姿态动力学模型融合到姿态确定算法中，实现了高精度的姿态确定。

3.1.3 复合姿态确定方法

复合姿态确定是利用静态姿态确定方法的优势进一步提升动态姿态确定精度的方法，其结构框图如图8 所示。通过静态姿态确定方法，将星敏感器、磁强计和太阳敏感器等确定性姿态信息进行融合，直接提供姿态四元数作为卡尔曼滤波器的测量输入，降低了观测模型的复杂度和非线性度。同时，静态姿态确定方法给定的姿态信息精度更高，信息量更加充足，可有效提高动态姿态确定的精度。

图8 复合姿态确定方法结构框图Fig.8 Structure diagram of composite attitude determination

文献［42］利用QUEST 方法，根据星敏感器的恒星矢量观测数据求解姿态四元数作为MEKF 方法的观测输入，实现了姿态确定误差、陀螺零偏误差和标度因数误差的最优估计，确保了高精度的姿态确定。同样地，文献［43］利用Q 方法，根据姿态矢量观测值解算姿态四元数，并平滑地融入MEKF 方法，有效简化了非线性方程的求解和迭代计算过程，实现了平稳高效的姿态确定。为了进一步提升姿态确定系统的精度，文献［32］和［44］利用SVD 方法求解得到静态姿态信息及其误差协方差矩阵，并分别作为卡尔曼滤波器的观测输入和观测噪声矩阵，实现了自适应的姿态状态估计，保证了优良的姿态确定精度。

综上所述，复合姿态确定方法不仅提升了卫星姿态确定的精度，还兼顾了系统的稳定性与运行效率。特别是利用静态姿态确定方法提供观测四元数和观测噪声矩阵，实现动态自适应姿态估计的方法，是未来进一步提高姿态确定精度的研究方向。

3.2 精密姿态控制技术

空间环境干扰、转动惯量参数不确定性、执行机构力矩误差等问题是影响卫星姿态控制精度的主要因素。在大角度姿态机动过程中，控制模型的耦合特性会严重影响姿态控制的收敛速度与稳定度。因此，精密姿态控制的研究重点是要确保姿态控制器具备解耦控制、及抑制干扰和模型参数不确定性影响的能力。

3.2.1 干扰观测控制方法

卫星的外部干扰会直接导致姿态控制误差，甚至影响系统的稳定性。积分控制虽然可以补偿时不变干扰的影响，但是它对动态时变干扰的抑制能力有限。在经典控制理论中，干扰（包括时不变和时变干扰）的抑制能力通过控制系统的开环增益来表征，系统的稳态误差为干扰幅值与系统开环增益的比值。然而，增大开环增益意味着增大系统的控制带宽，实际的工程系统中受限于计算机的运算能力、传感器的测量能力和执行机构的响应能力，控制带宽不可能无限制增大，从而限制了系统对于干扰的抑制能力。

基于干扰观测器的控制（Disturbance Observer Based Control，DOBC）及其相关方法在各控制领域得到了广泛的研究和应用［45-46］。这类方法的核心思想是将系统的扰动及模型参数不确定性视为集中干扰，利用干扰观测器［46］或扩张状态观测器［47］对总的干扰进行估计，通过前馈控制减弱甚至直接消除干扰的影响，最终实现精确的跟踪控制［48］。文献［49］利用干扰观测器，精准估计了执行机构故障、参数不确定和外部干扰的总扰动，并通过反馈控制抑制了集中干扰的影响。为了进一步提升干扰的抑制能力，文献［50］设计了一种干扰观测器和自抗扰控制相结合的抗干扰强化控制方法，通过两种方法的优势互补，进一步增强了干扰的抑制能力，提高了姿态控制系统的性能。文献［51］利用线性矩阵不等式，实现了干扰观测器和鲁棒控制器的联合设计，在模型参数不确定性、测量误差和执行器故障条件下确保了优良的姿态跟踪控制性能。

3.2.2 鲁棒自适应控制方法

鲁棒自适应控制方法（Robust Adaptive Control，RAC）通过实时调节控制器参数来抑制干扰和模型不确定性引发的控制误差［52］。相比干扰观测控制方法，自适应控制方法利用其学习调节特性，在处理慢变扰动和卫星转动惯量参数不确定的问题上更具优势［53］，确保了高性能的跟踪控制和良好的稳定性。针对存在未知外部扰动的航天器姿态控制问题，文献［54］利用功率积分技术设计了自适应控制器，抑制了干扰的影响并保证了姿态控制的平稳性。针对存在惯量不确定性的航天器控制问题，文献［55］建立了质心变化导致惯量时变的姿态动力学，利用自适应技术的学习能力设计了复合自适应控制器，实现了姿态跟踪控制误差的有限时间收敛。

此外，自适应控制方法可以利用神经网络［56］或模糊逻辑［57］逼近估计未知的模型特性和外部干扰，提高控制系统的瞬态性能；也可以通过迭代学习方法不断学习优化控制参数［58］，使得固定应用场景的控制性能达到最优［59］。文献［60］利用神经网络逼近卫星的未知模态，结合滑模控制理论构造了神经自适应观测器，准确估计了未知模态，并用于反馈控制器的设计。文献［61］利用自适应T-S 模糊逻辑结合干扰观测器，抑制了多源干扰对航天器姿态的影响，实现了高精度的姿态跟踪控制。文献［62］提出了一种自适应迭代学习控制方法，通过不断迭代更新控制器参数，可以有效地处理初始对准误差和惯量不确定问题，确保高性能的动态跟踪控制，适用于立体成像和多条带成像这类固定角度机动的成像控制场景。

3.2.3 滑模控制方法

滑模控制方法（Sliding Mode Control，SMC）在处理非参数不确定性以及高频率外部扰动问题上更具优势，可保证控制系统状态的有限时间收敛，结构简单稳定性强［63］。针对航天器存在模型不确定性和外部扰动下的姿态控制问题，文献［64］利用预设性能理论，结合滑模控制实现了姿态的有限时间收敛，并通过三轴气浮台对所提方法进行了验证。针对航天器的执行机构故障问题，文献［65］利用非奇异终端滑模控制和有限时间干扰观测器实现了全局稳定控制，有效地抑制了瞬态执行机构故障的影响，表现出优良的稳定性。为了进一步提升控制系统的性能，文献［66］综合自适应控制方法和滑模控制方法的优势，提出了航天器姿轨一体化自适应滑模控制方法，实现了高精度的姿态轨道联合控制。

然而，滑模控制器中符号函数项生成的切换控制会导致高频抖振问题，严重影响高分辨率遥感卫星的成像质量。工程上一般利用饱和函数或者双曲正切函数替换符号函数解决抖振问题［67］，但是一定程度上会降低系统的稳定性［68］。随着滑模控制理论的发展，Levant 提出了高阶滑模控制方法［69］，可以在保证系统鲁棒性的前提下解决滑模控制的抖振问题。文献［70］利用二阶滑模控制方法设计了准连续趋近控制器，在航天器存在执行机构故障和外部干扰的条件下实现了高精度的姿态控制，并有效地抑制了滑模控制的抖振。文献［71］利用自适应控制的低控制增益特性，提出了一种连续的自适应二阶滑模控制方法，在保证状态变量快速收敛的同时，更加有效地降低了控制抖振。

综上所述，为了实现卫星姿态的精密控制，在系统设计过程中，要重点关注干扰和模型参数不确定性的抑制及多输入多输出的解耦控制问题。干扰观测控制、自适应控制和滑模控制技术具备实现精密姿态跟踪控制的能力，但是相对缺乏工程应用经验。在后续研究中，可汲取上述控制方法的优势，逐步与经典控制方法相融合，以基准控制器结合附加控制器的控制框架进行系统设计（如比例微分控制结合干扰观测器），在确保稳定可靠的前提下，不断提升卫星姿态控制的性能。

3.3 敏捷姿态控制技术

光学遥感卫星实现敏捷姿态控制的方法可以分为两个技术途径：第一种是配置可以输出大力矩的控制力矩陀螺，缩短卫星姿态机动过程中的角速度加减速过程，提高卫星的姿态机动能力；第二种是对于配置反作用飞轮的卫星系统，通过对姿态机动路径进行规划，最大限度挖掘反作用飞轮的控制能力，实现姿态的敏捷机动。

3.3.1 基于控制力矩陀螺的敏捷姿态控制

控制力矩陀螺由飞轮安装在伺服框架上构成，利用伺服框架调整动量轮的方位，进而产生陀螺力矩。由于控制力矩陀螺具备大力矩、低功耗、控制速度范围广、动态响应特性高的特点，被广泛应用于卫星的敏捷姿态控制［72-73］。

控制力矩陀螺在控制过程中存在奇异点，其操纵率是控制系统设计的重点与难点。文献［73］提出了一种控制力矩陀螺和反作用飞轮协同的混合执行机构控制方法，利用控制力矩陀螺的强大能力确保系统的敏捷机动特性，结合反作用飞轮规避了奇异控制问题，显著提高了航天器的动态性能与稳态精度。文献［74］研究了基于单框架定转速控制力矩陀螺的航天器自适应姿态控制，不仅规避了控制奇异点，还保证了转动惯量时变和执行机构非对准条件下的姿态控制性能。文献［75］提出了一种力矩最优控制方法，通过设置最优的控制力矩陀螺初始框架角，实现了最短姿态路径的机动控制，该控制方法成功应用于典型光学遥感卫星的多点成像任务，证明了其优越的机动性能和稳定性。

3.3.2 基于姿态规划的敏捷姿态控制

小型光学遥感卫星由于成本、体积和质量的限制，姿态控制系统多采用反作用飞轮作为执行机构。相比于控制力矩陀螺，反作用飞轮虽然控制力矩较小，但是具备隔振系统简单、可靠性高和成本低廉的优点。在小控制力矩条件下，对姿态机动路径进行规划并设计合理的控制器可以有效提高卫星的姿态机动能力［76］。

基于姿态机动路径规划的思想，小型月球探测器［77］执行对月成像任务期间，设计了一种Bang Coast Bang 姿态路径规划方法，将角加速度划分为加速、匀速和减速三段，结合PID 控制器实现了反作用飞轮角动量和控制力矩受限条件下的大角度敏捷机动控制。为了提高Bang-Bang逻辑姿态轨迹的平稳性，文献［78］借鉴轨道控制的霍曼转移方式优化姿态的加减速过程，实现了平稳的近时间最优姿态机动控制。为了实现模型参数不确定和外部干扰条件下的敏捷姿态控制，文献［8］提出了一种控制能力约束条件下的姿态规划方法，结合专用的鲁棒干扰观测控制器，实现了光学遥感卫星精密敏捷的姿态控制，可高效完成多目标点成像任务。

总体而言，基于姿态机动路径规划的控制方法可在控制能力受限的条件下，实现优越的姿态机动性能，具有更大的研究价值和潜力。在今后的研究中，可将姿态机动路径规划与干扰观测控制、自适应控制和滑模控制等方法紧密结合，以确保卫星姿态控制系统能够同时具备精密性和敏捷性。

3.4 小 结

本节以模块化的形式，从姿态确定单元，姿态规划单元和姿态控制单元三个方面对光学遥感卫星精密敏捷姿态控制的关键技术和最新进展进行了概要介绍。特别注意的是，部分先进方法仍处于探索阶段，在实际工程中，需要针对具体需求和实际问题开展研究和分析，以成熟技术为基础，逐步利用先进技术设计精密敏捷的姿态控制系统，促进高质量、智能化的成像控制系统发展。

4 一体化成像控制技术研究展望

光学遥感卫星控制系统的姿态确定单元、姿态规划单元和姿态控制单元相互耦合，共同决定姿态控制的快速性、准确定和稳定性。图9 总结了基于干扰观测的精密敏捷控制方法，详细说明了在传感器精度约束、执行机构能力约束、空间环境干扰约束下的精密敏捷控制框架。总体而言，控制系统的设计要充分考虑成像任务需求以及面临的实际问题，协调平衡各个单元，从总体设计的角度对精密敏捷姿态控制系统进行一体化设计。

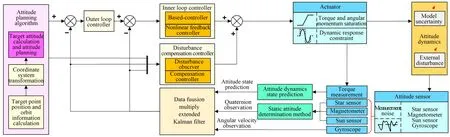
图9 基于干扰观测的精密敏捷控制结构框图Fig.9 Structure diagram of disturbance observer-based precision and agile control

4.1 成像控制系统优化设计

光学遥感卫星控制系统的部组件是根据经验选定的，利用仿真技术进行迭代分析和设计，以满足成像任务的需求。随着低成本、多功能和集成化的卫星设计发展，传统的设计方法已无法兼顾各个指标要求。针对利用卡尔曼滤波器实现多传感器数据融合的算法框架，文献［79］利用凸优化方法，在满足给定估计误差约束的前提下确定最优的传感器参数，解决了总体指标约束下的低成本传感器选型问题。

从成像任务的需求出发构建成像控制的整体模型，优化系统设计，具备巨大的应用价值。首先，根据成像任务的需求，明确对卫星精密性与敏捷性的性能指标。同时，根据卫星控制系统的组成，建立精确的传感器、执行机构和卫星姿态动力学模型，结合姿态确定与控制原理，分析卫星传感器、执行机构、姿态确定与控制方法对系统性能指标的影响因数。在此基础上，构建控制系统与精密性和敏捷性指标的整体模型，全面理解控制系统各单元和部组件与总体指标之间的关系。最后，以成像任务分解的控制指标要求作为系统约束，以凸优化方法或迭代学习方法优化系统传感器、执行机构的参数，在低系统成本的条件下满足成像系统需求，确保高质量成像。

4.2 多源姿态信息融合

姿态确定系统的主要传感器包括确定性姿态传感器（星敏感器，磁强计，太阳敏感器）和角速度传感器（陀螺仪）。姿态确定方法则可以分为两个技术途径：对于配置确定性姿态传感器和陀螺仪的系统，根据卫星的姿态运动学方程，利用卡尔曼滤波器进行数据融合确定姿态；对于无陀螺仪的系统，根据卫星的姿态运动学和动力学方程，以执行机构的控制力矩作为输入信息进行姿态预测，确定性姿态传感器的测量姿态作为观测信息，利用卡尔曼滤波器同时确定高精度的姿态和角速度估计信息。

从姿态确定精度、收敛速度和成本等方面来看，上述两个技术途径各有优缺点。此外，现有研究更多地关注姿态确定方法本身的设计，缺乏对传感器特性的认识和系统性的理解。为了进一步提升现有姿态确定系统的精度和可靠性，根据最优状态估计理论，将上述两个技术途径的优点互补，建立一个高维姿态确定模型，将系统已有的测量信息充分结合卫星的姿态运动学和动力学方程。如图9 所示的姿态确定方法结构框图，描述了利用卫星的姿态动力学和反作用飞轮的控制力矩信息预测卫星的姿态状态。同时，利用静态姿态确定方法提供高精度的姿态四元数观测信息，利用陀螺仪提供角速度观测信息。最后，通过MEKF 方法实现多源姿态及相关信息的数据融合，不仅可以提高姿态确定系统的精度，还可在部分传感器故障的条件下保证系统的可靠性。

4.3 姿态与执行器一体化控制

根据图9 可知，精密敏捷姿态控制模块的输出为发送给执行机构的控制信号，执行机构根据控制信号输出控制力矩操控卫星的姿态，因此执行机构的能力是决定姿态控制系统性能的关键因素。在文献［8］中，姿态规划单元通过规划姿态机动路径来匹配反作用飞轮的控制能力约束，最大限度地发挥系统潜在能力，实现敏捷机动控制。

反作用飞轮本身为一个电机闭环控制系统，姿态控制与电机控制分别单独设计时，两者之间必然存在着一定的控制性能不匹配，这在一定程度上会降低整体控制性能，而现有的设计方法并未关注此问题。为了进一步改进卫星姿态控制系统的精密性和敏捷性，应建立卫星姿态与反作用飞轮电机一体化的控制系统模型，逐步设计卫星姿态外环控制器、内环控制器，反作用飞轮转速环控制器和电流环控制器，实现综合协调的姿态与执行器一体化控制。

5 结论

光学遥感卫星姿态控制系统的精密性与敏捷性是多功能、高质量成像的关键，如何在复杂的约束条件下实现高性能的姿态控制，是光学遥感卫星研制的关键。本文从卫星成像的角度出发，分别论述了姿态机动能力与复杂成像功能、姿态确定精度与图像几何精度、姿态控制精度与成像传递函数的关系，分析了超稳定、超精确、超敏捷控制对多功能、高时效、高分辨率成像的意义。基于成像控制需求，将卫星姿态控制系统分为姿态规划单元、姿态确定单元和姿态控制单元三部分，深入论述了各个单元涉及的关键技术和最新进展，对相应的技术及其应用进行了深入的探讨和总结。为了充分挖掘卫星姿态控制系统潜能，进一步提升成像控制系统的性能，应充分发挥集成化设计的技术优势，在明确姿态控制系统各单元耦合关系的基础上，建立统一的控制系统模型，采用综合协调的思想，从精密敏捷姿态控制系统一体化设计方面进行深入研究，推动低成本、高可靠、高性能成像控制系统的发展。