考虑点蚀情况的双渐开线齿轮动态特性研究*

沈 成,姜 宇,姜春雷,潘 毅,樊智敏

(青岛科技大学 机电工程学院,山东 青岛 266061)

0 引 言

齿轮作为机械传动系统中的核心部件,点蚀与磨损是其失效的主要形式。齿面一旦发生点蚀,齿轮的传动精度、承载能力、工作寿命和效率就会降低。点蚀坑数量增加,会导致接触线长度发生变化,从而影响齿轮的啮合刚度,其动力学特性也会随之变化。

因此,开展点蚀对双渐开线齿轮的接触线长度与啮合刚度影响的研究,对研究其动力学特性有重要意义。

近年来,国内外学者对点蚀情况下齿轮的时变啮合刚度及动力学特性进行了不同深度的研究。

冯松等人[1]研究了齿面磨损对齿轮啮合刚度的影响,考虑轮齿弯曲变形、剪切变形等,计算分析了微观点蚀及宏观点蚀下的啮合刚度及发展规律。林腾蛟等人[2]研究了裂纹故障对斜齿轮的时变啮合刚度及振动响应的影响,采用能量法建立了齿根裂纹故障的悬臂梁模型,并对齿轮动力学特性进行了研究。赵鑫等人[3]基于能量法建立了轮齿悬臂梁模型,研究了不同点蚀位置、深度、数量对啮合刚度的影响。陈勇等人[4]研究了不同点蚀程度对斜齿轮动力学特性的影响,建立了齿轮多体动力学模型,并通过实验研究了点蚀对齿轮振动加速度的影响。QIN Wei-jie等人[5]基于多疲劳机理的方法,在考虑摩擦的基础上,研究了转速对齿轮应力分布的影响,并预测了齿轮产生疲劳裂纹的加载规律。冯伟等人[6]利用铁谱分析和振动分析,模拟了点蚀故障齿轮啮合过程中的磨损与振动的关系。MA Rui等人[7]推导出发生齿面点蚀剥落的遏制齿轮的时变啮合刚度计算式,研究了齿面点蚀对其时变啮合刚度的影响。李纪强等人[8]探讨了工程中微点蚀与热胶合发生的损伤原理,分析了润滑油膜厚度和瞬时啮合温度的影响。涂旭欣等人[9]研究了点蚀发生时齿面剥落形状及分布对齿轮时变啮合刚度的影响。HAN Lin等人[10]以齿面点蚀剥落的斜齿轮为研究对象,给出了发生点蚀后的斜齿轮时变啮合刚度计算式。

根据以上研究发现,在发生点蚀失效情况下,齿轮动力学特性的研究大多针对目前工业体系中的常见齿轮,对双渐开线齿轮的研究较少。

双渐开线齿轮是一种综合了双圆弧齿轮优点和渐开线齿轮优点的新型齿轮,目前对双渐开线齿轮动态特性的研究已取得了一些成果。樊智敏等人[11]提出了一种基于有限元法建立的双渐开线齿轮啮合刚度计算模型,求解了双渐开线齿轮时变啮合刚度,发现了双渐开线齿轮综合时变啮合刚度变化趋势与普通渐开线齿轮相似。陈亮等人[12]基于赫兹接触理论和分形理论,建立了考虑分形齿面粗糙度的双渐开线齿轮时变啮合刚度模型,分析了摩擦系数、分形维数以及粗糙度幅值等对双渐开线齿轮时变啮合刚度的影响。

但目前尚未有学者对双渐开线齿轮发生疲劳点蚀情况下的啮合刚度及动力学特性进行研究。

笔者建立轮齿载荷和轮齿变形的比值关系,研究发生点蚀时的双渐开线齿轮啮合刚度,并其与有限元法结果进行对比,以验证该方法的准确性;建立发生点蚀时双渐开线与普通渐开线齿轮的动力学模型,在不同点蚀情况下,研究双渐开线齿轮与普通渐开线齿轮动态啮合力及振动加速度的时域变化规律。

1 齿轮点蚀动力学模型

齿面点蚀是齿轮传动中常见的失效形式之一。点蚀可分为几个阶段。点蚀状态分为均匀磨损、微点蚀、宏观点蚀;宏观点蚀又分为初期点蚀、扩展性点蚀、片蚀或剥落。

早期的点蚀多是由于啮合初期齿面存在微小凸起,接触时产生较大的应力,从而产生点蚀;在齿轮多次啮合之后,多数均匀磨损变为微点蚀;在早期微点蚀的基础上,经过长期的双齿啮合冲击,在靠近节线的位置出现宏观点蚀[13]。

双渐开线齿轮基本齿廓如图1所示。

图1 双渐开线齿轮基本齿廓

双渐开线齿轮是以普通渐开线齿轮齿廓为基准齿廓,对齿根进行切向正变位,对齿顶进行切向负变位,其基本齿廓包括齿根过渡圆弧AB、齿根直线BC、半径为ρg齿腰过渡圆弧CD、齿顶直线DE。

齿根过渡圆弧与齿根直线在B点相切,齿腰过渡圆弧CD与齿顶直线DE相切于D点、与直线BC相交于C点[14]。

为了更加直观地分析齿轮啮合过程,笔者将双渐开线齿轮啮合平面沿基圆柱展开,考虑发生宏观点蚀情况下,接触线长度随时间变化情况如图2所示。

图2 双渐开线齿轮啮合平面沿基圆柱展开图

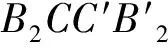
考虑宏观点蚀发生在节线靠近齿根附近,为5个沿齿面方向的圆形点蚀,在该工况下不同时刻的接触线长度可表示为:

(1)

其中,tB2C=lB2C/rb1ω1,tB2P1=lB2P1/rb1ω1,tB2E=(lB2E-l_)/rb1ω1,tB2E1=(lB2E1-l_)/rb1ω1,并依次计算tB2X、tB2D1、tB2E3、tB2E4、tB2B1、tB2F、tB2G、tB2H。

为使研究方便,假设均匀分布的5个直径为1 mm圆形点蚀坑,在这里设置的初期点蚀为5个沿齿向方向的点蚀坑,称为点蚀1情况;齿轮经长时间啮合初期点蚀变为沿齿向方向10个点蚀坑,称为点蚀2情况;又经长时间啮合,其在齿面沿齿向方向变为15个点蚀坑,称为点蚀3情况。

3种齿面点蚀情况如图3所示。

图3 双渐开线齿轮的不同点蚀情况

不同点蚀情况下的双渐开线齿轮接触线长度如图4所示。

图4 不同点蚀状态下的双渐开线齿轮接触线长度

从图4可以看出:在3种不同点蚀情况下,在主动轮齿进入啮合时,双渐开线齿轮单齿接触线长度逐渐增大,其未受到点蚀坑影响出现突变;啮合进行到齿腰分阶位置时,接触线长度因点蚀坑影响发生2次突变,接触线长度减小;随着啮合的进行,主动轮进入啮合向齿顶啮合区移动,接触线长度逐渐增大并在达到最大值后保持不变,此时点蚀情况最为严重,接触线长度共发生3次突变;随着轮齿退出啮合,接触线长度逐渐减小,期间未受点蚀坑影响,整个啮合过程中接触线长度共发生5次突变,这与数学模型变化一致;点蚀坑对接触线长度的影响主要发生在主动轮轮齿进入啮合时,在3种不同点蚀情况下,随着点蚀坑数量的增加,接触线长度突变值增大[15]。

2 点蚀情况下双渐开线齿轮时变啮合刚度

刚度激励是指齿轮在啮合过程中由于啮合刚度的时变性而产生的动态激励。作为齿轮系统内部激励的重要激励形式,刚度激励对齿轮系统的动态性能有着很大的影响。

啮合刚度可以用来表征轮齿抵抗变形的能力,通常将单齿抵抗变形的能力称为单齿啮合刚度,将参与啮合的各对轮齿之间的综合效应称之为综合啮合刚度。综合啮合刚度与轮齿的综合弹性变形、轮齿啮合对数以及齿轮的材料等因素有关[16]。

笔者考虑点蚀情况发生时,点蚀坑对齿轮接触线长度的影响,研究不同点蚀数量对双渐开线齿轮啮合刚度的影响。

假设在齿轮啮合过程中,轮齿上所受载荷在接触线上呈均匀分布,并且轮齿变形也是沿接触线方向呈均匀分布,则两者的比值即啮合刚度,可近似认为其只与接触线的长度有关,并且呈正比关系,计算公式如下[17]:

kt=k0lt

(2)

式中:kt为时变啮合刚度;lt为总接触线长度;两者均与时间有关,具有时变性;k0为比值系数。

由式(2)可知,啮合刚度的时变性主要与接触线的时变性有关,接触线的时变性主要是由啮合齿对的交替变化所致,三者的时变周期一致,都为轮齿的啮合周期T。

根据ISO 6336—1:2006圆柱直齿轮和斜齿轮疲劳强度与弯曲强度计算国际标准,斜齿轮单齿啮合刚度的最大值为:

(3)

式中:CM为理论修正系数,CM=0.8;CR为轮坯结构系数,CR=1;CB为基本齿廓系数,CB=1;β为齿轮螺旋角,β=8°6′34″。

(4)

(5)

齿轮啮合刚度均值的计算公式为:

cγ=(0.75εα+0.25)c′

(6)

式中:εα为端面重合度。

不同点蚀情况下的双渐开线齿轮时变啮合刚度如图5所示。

图5 不同点蚀情况下的双渐开线齿轮时变啮合刚度

由图5可知:轮齿啮合期间,齿轮啮合刚度随着时间变化不断增加,在点蚀1与点蚀2情况下,单齿啮合刚度差别不大;相较点蚀1、点蚀2,点蚀3情况发生时,点蚀坑扩展至靠近齿根位置,单齿啮合刚度明显减小。

观察齿轮啮合时啮合刚度的变化,可以发现点蚀坑增加,即轮齿在啮合过程中接触面积减小,导致齿轮啮合刚度降低。

假设一对齿轮在节点均匀接触,将齿轮接触单位面积的法向载荷与轮齿齿面法向综合变形量的比值称为对轮齿的单齿啮合刚度kf,公式为:

(7)

式中:Fn为齿面法向载荷;b为齿宽;δ为轮齿齿面法向综合弹性变形。

齿轮从上一轮齿退出啮合开始到下一轮齿进入啮合的过程称为一个啮合周期,在此期间主动轮转过的角度被称为转角,其值:φ=2π/z1。

笔者建立3种点蚀情况下的双渐开线齿轮啮合有限元模型,将每对齿轮20等分,生成21个不同角度的仿真模型,并进行瞬态动力学分析。

因为在ANSYS中提取各轮齿变形量存在误差,且计算过程比较复杂,所以笔者采取一种快捷方法,首先提取主动轮的角变形量,利用公式求得齿轮的扭转啮合刚度,再根据扭转啮合刚度与啮合刚度之间的比值关系求出齿轮的啮合刚度。

齿轮扭转啮合刚度kt为:

(8)

式中:T1为主动轮输入转矩;Δθ为主动轮角变形量。

单齿啮合刚度kn为:

(9)

笔者在齿轮中一个轮齿的齿面建立符合图3的3种点蚀坑,将齿轮啮合模型导入到ANSYS中的Transient Structural模块,并进行仿真设置,求得双渐开线齿轮主动轮的角变形量Δθ与啮合刚度,如表1所示。

表1 双渐开线齿轮有限元仿真数据

双渐开线齿轮有限元分析模型如图6所示。

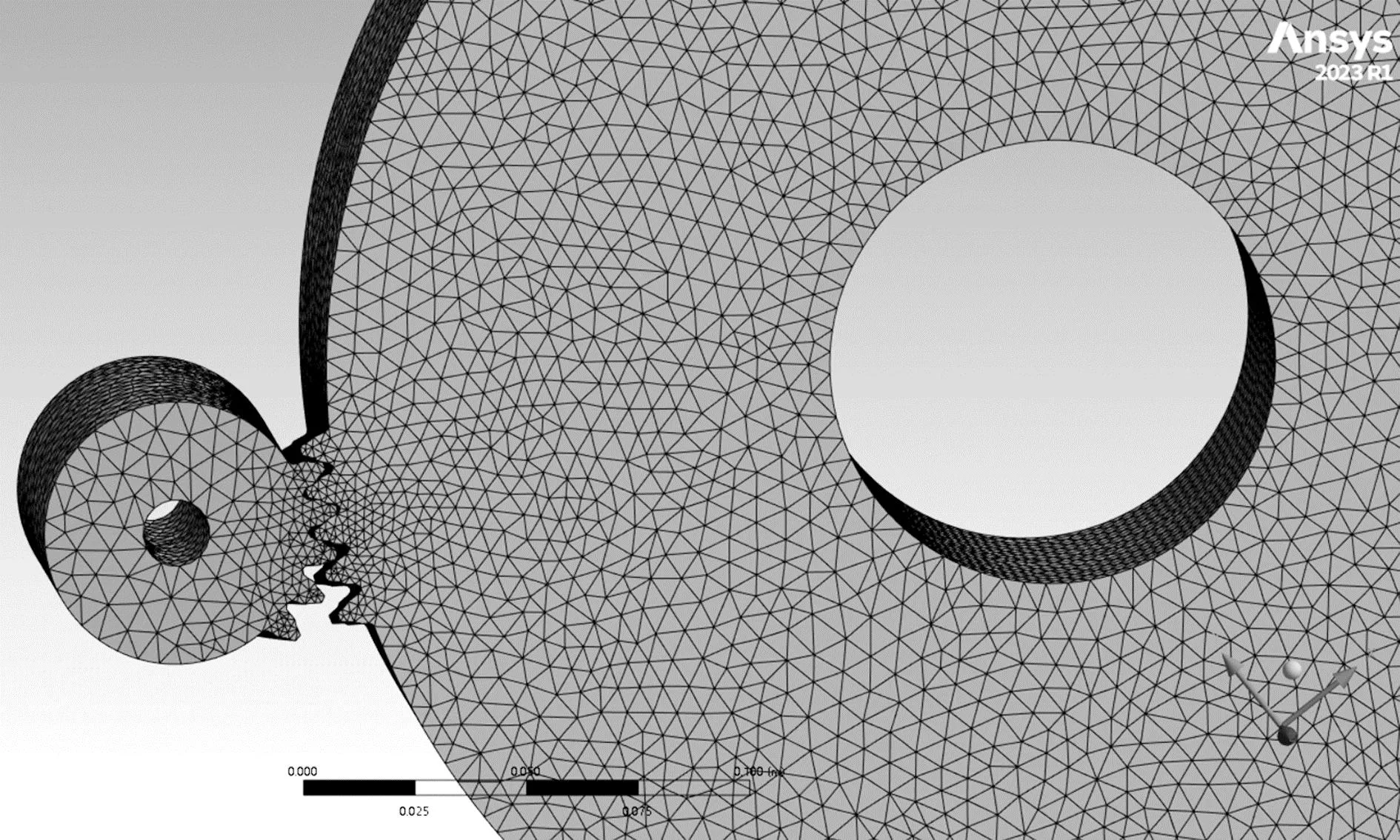
图6 双渐开线齿轮有限元分析模型

笔者将双渐开线齿轮与普通渐开线斜齿轮在3种点蚀情况下的有限元仿真数据、双渐开线齿轮接触线长度计算的单齿啮合刚度矩阵导入MATLAB软件,对三组数据进行曲线拟合,得到两种齿轮的单齿啮合刚度,点蚀1、点蚀2、点蚀3情况,即双渐开线-普通渐开线齿轮点蚀情况下单齿啮合刚度对比情况,如图7所示。

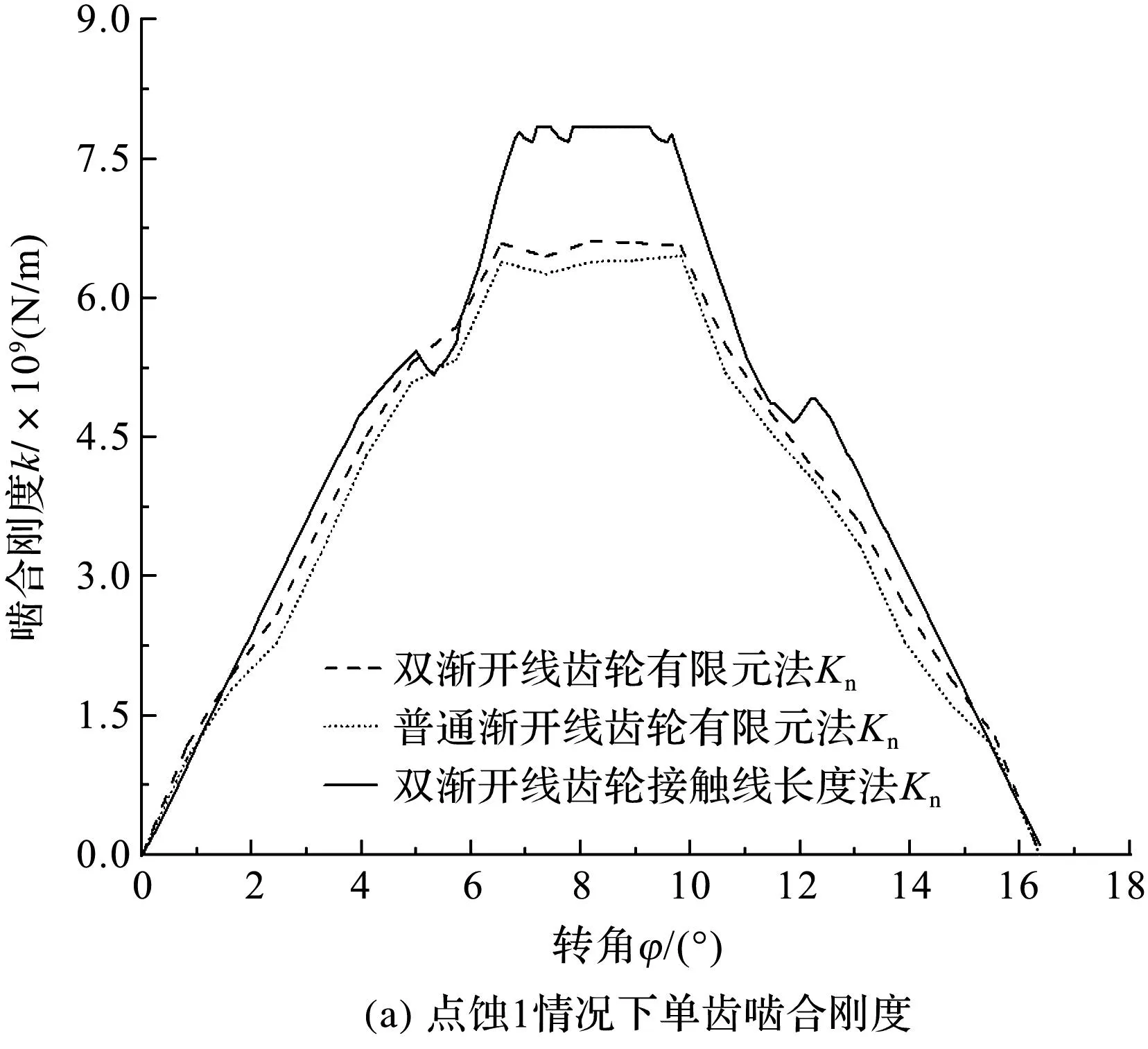
图7 双渐开线-普通渐开线齿轮点蚀情况下单齿啮合刚度对比

由图7可知:接触线长度法与有限元法求解齿轮啮合刚度的变化趋势大体相同;点蚀情况发生时,两齿轮啮合刚度值均减小,随着点蚀坑的增加,齿轮啮合刚度变化明显,接触线长度法计算出的齿轮啮合刚度大于有限元法计算出的刚度;点蚀1与点蚀2情况发生时,两种方法计算的啮合刚度变化趋势相同,点蚀3情况发生时,点蚀坑的位置不断向齿根位置靠近,有限元法求解的啮合刚度小于接触线长度计算的啮合刚度。

对比双渐开线齿轮与普通渐开线齿轮的啮合刚度,在一个啮合周期内其变化规律大致相同;在点蚀情况下,双渐开线齿轮由于齿根增厚,其单齿啮合刚度要大于普通渐开线齿轮的刚度。

综上所述,两种方法计算齿轮的啮合刚度总体变化趋势相同,总体数值在同一量级,且均表现出点蚀情况下的齿轮啮合刚度变化。

3 点蚀情况下双渐开线齿轮动力学特性

在考虑点蚀的情况下,笔者建立同参数、同工况的双渐开线齿轮与普通渐开线齿轮的柔性多体动力学模型,研究点蚀发生对两齿轮动力学特性的影响。

双渐开线齿轮齿面点蚀模型,即发生点蚀1、点蚀2、点蚀3情况的齿轮轮齿模型如图8所示。

图8 双渐开线齿轮齿面点蚀模型

3.1 双渐开线-普通渐开线齿轮传动动态接触力

笔者对同参数、同工况下的双渐开线-普通渐开线齿轮进行动力学仿真分析(为防止启动时转速的突变,驱动与负载均采用Step渐进函数施加),综合分析不同点蚀故障对齿轮动态啮合力的影响。

点蚀1情况下齿轮动态啮合力时域图如图9所示。

图9 点蚀1情况下动态啮合力时域图对比

点蚀2情况下齿轮动态啮合力时域图如图10所示。

图10 点蚀2情况下动态啮合力时域图对比

点蚀3情况下齿轮动态啮合力时域图如图11所示。

图11 点蚀3情况下动态啮合力时域图对比

由图9～图11可以看出:随着点蚀程度的不断加深,双渐开线齿轮与普通渐开线齿轮的啮合力幅值波动越来越大,双渐开线齿轮啮合力最大值1.24×105N,普通渐开线齿轮啮合力最大值为1.01×106N,对比两齿轮整体啮合力均值与最大幅值,可发现普通渐开线齿轮在点蚀坑增加时,其啮合力的变化范围、啮合力均值及增加值均大于双渐开线齿轮啮合力的变化范围、啮合力均值及增加值。

综上可知,点蚀常发生在节线靠近齿根位置时,由于双渐开线齿轮齿腰的分阶特点,齿根厚度大于普通渐开线齿轮,在点蚀发生时,其动态啮合力最大幅值及均值小于普通渐开线齿轮的动态啮合力最大幅值及均值;点蚀情况下,双渐开线齿轮抵抗啮合冲击的能力更强,承受动态冲击的能力要优于普通渐开线。

3.2 双渐开线-普通渐开线齿轮传动振动角加速度

齿轮通过啮合轮齿间的接触来传递动力,齿面点蚀导致齿轮在传动过程中产生振动冲击,进而导致齿轮动态啮合力幅值的波动。齿轮啮合时,接触力的变化会影响传动过程中角速度、角加速度的波动。

笔者将根据不同点蚀情况分析双渐开线与普通渐开线齿轮振动角加速度的变化情况。

点蚀1情况下从动轮角加速度时域图对比如图12所示。

图12 点蚀1情况下从动轮角加速度时域图对比

点蚀2情况下从动轮角加速度时域图对比如图13所示。

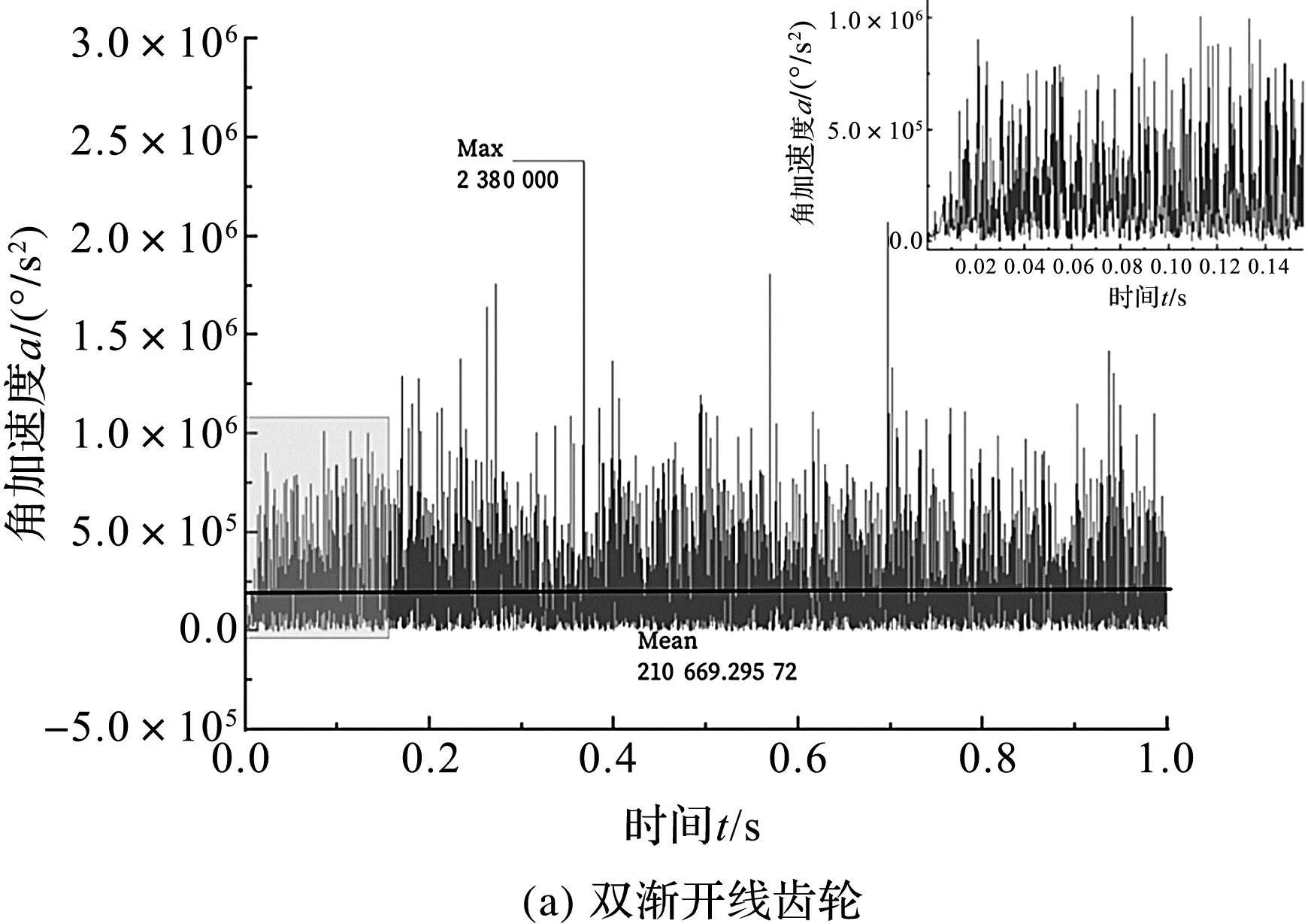
图13 点蚀2情况下从动轮角加速度时域图对比

点蚀3情况下从动轮角加速度时域图对比如图14所示。

图14 点蚀3情况下从动轮角加速度时域图对比

从图12～图14中可以看出:普通渐开线齿轮角加速度整体波动大、峰值高,最大值为3.012×107°/s2;双渐开线齿轮在0～0.02 s内呈加速上升状态,角加速度波动较稳定,最大值为2.66×106°/s2,不会产生过大的冲击,速度变化整体优于普通渐开线齿轮的速度变化;齿面点蚀由点蚀1扩展为点蚀3,两齿轮的振动角加速度最大值均有所增加,双渐开线齿轮振动角加速度的幅值变化小于普通渐开线齿轮的幅值变化,角加速度幅值分布集中,未有较大突变值。

因此,点蚀发生时双渐开线齿轮抵抗冲击的能力较强,动力传递的稳定性优于普通渐开线齿轮的稳定性,传动过程较平稳。

4 结束语

笔者研究了双渐开线齿轮不同点蚀情况下接触线长度及时变啮合刚度的变化规律,用有限元法验证了接触线长度计算啮合刚度的准确性;建立了点蚀情况发生时双渐开线与普通渐开线齿轮柔性多体动力学模型;分析了不同点蚀情况对两齿轮动态啮合力及振动加速度的影响。

研究结果表明:

1)点蚀发生时,双渐开线齿轮轮齿进入啮合后接触线长度发生变化,在轮齿退出啮合时接触线长度不发生变化;

2)随着点蚀程度的加深,两种类型齿轮啮合刚度均不断减小,其中双渐开线齿轮在点蚀影响下的啮合刚度变化稳定,抵抗冲击能力优于普通渐开线齿轮的抗冲击能力;

3)同工况条件下,随着点蚀程度的加深,两种类型齿轮动态啮合力及振动角加速度幅值增加,双渐开线齿轮啮合力最大值为1.24×105N,角加速度最大值为2.66×106°/s2,普通渐开线齿轮啮合力最大值为1.01×106N,角加速度最大值为3.012×107°/s2;可见,双渐开线齿轮的加速度幅值波动较平缓,动力传递稳定性优于普通渐开线齿轮的稳定性。

笔者后续的研究方向为:1)不同工况下双渐开线齿轮的齿面形貌,安装误差等的动力学特性;2)研究双渐开线齿轮瞬态接触下的齿面油膜压力分布、摩擦因数等瞬态接触特征量的提取方法,及其对动载荷的影响规律。