不确定转子系统动力学降阶模型构建与模型散度参数辨识*

张义彬,刘保国,2*,刘彦旭,励精为治

(1.河南工业大学 机电工程学院,河南 郑州 450001;2.河南省超硬磨料磨削装备重点实验室,河南 郑州 450001)

0 引 言

转子系统作为航空发动机、燃气轮机等大型复杂旋转机械的核心部件,在其设计、加工、制造、安装和运转工作过程中普遍存在着不同因素导致的各种不确定性。比如,在转子系统启动过程时,因为材料磨损导致几何尺寸的不确定性[1-3],高温工作环境导致转子系统支承刚度的不确定性[4-5],外力干扰引起的载荷不确定性[6]等。

这些不确定性可以分为三类:1)系统自身结构的物理参数与几何参数随时间或环境的变化而产生的不确定性;2)外载荷的变异性引起的不确定性;3)模型简化引入的不确定性,即模型不确定性[7-8]。

在实际工程问题中,针对外载荷、支承刚度、节点质量、偏心距、转轴杨氏模量等参数不确定性,广泛采用的方法有摄动法[9]、多项式混沌展开[10-11]、广义多项式法[12-13]、蒙特卡洛模拟[14]等。这些方法虽然适用于处理参数不确定性,但并不适合用于处理模型简化引入的模型不确定性(如将转子简化为沿转轴轴线离散分布的集中质量点、模型降阶等)[15]。

为描述模型的不确定性,SOIZE C等人[16]提出了基于随机矩阵理论的非参数方法,并将其用于处理结构动力学系统建模过程产生的模型不确定性,研究了正定质量矩阵和刚度矩阵的非参数随机建模方法。WU H等人[17]基于最大熵原理和随机矩阵理论,提出了一种非参数Riccati整体传递模型。MATNEY A等人[18]提出了新的Galerkin降阶方法,从有限变形的热弹性单元导出了一组响应和温度耦合的非线型微分方程组。曹文博等人[19]提出了一种基于正交降阶模型和梯度优化以加速稳态流场的收敛方法。杨少冲等人[20]对动载荷作用下的结构损伤识别进行了研究,建立了反映结构状态的降阶模型,以解决未知载荷作用下多自由度结构动力分析计算量大且难以收敛的问题。郑伶华等人[21]针对高速飞行器机翼结构,采用POD分解和代理模型技术,建立了气动噪声的降阶分析模型。

以上考虑转子系统模型不确定性的文献都把计算模型的散度参数假设为已知范围内的数值[22],但SOIZE C等人[23]利用结构有限阶弹性模态的实验数据和对应的计算结果,可对散度参数进行辨识。

笔者采用非参数建模方法和矩阵降阶方法,构建模型不确定转子-支承系统的不确定动力学降阶模型;提出利用低阶临界转速及振动数据对降阶模型的散度参数进行辨识,以期为结构更加复杂的转子系统不确定性建模、振动响应预测等研究提供参考。

1 不确定动力学降阶模型

1.1 确定性动力学模型

典型双圆盘转子-支承系统如图1所示。

图1 转子-支承系统

图1的转子-支承系统中,将支承处简化为支承刚度和阻尼,将其余单元处简化为集中质量,其轮盘处存在陀螺效应,则系统计算模型如图2所示。

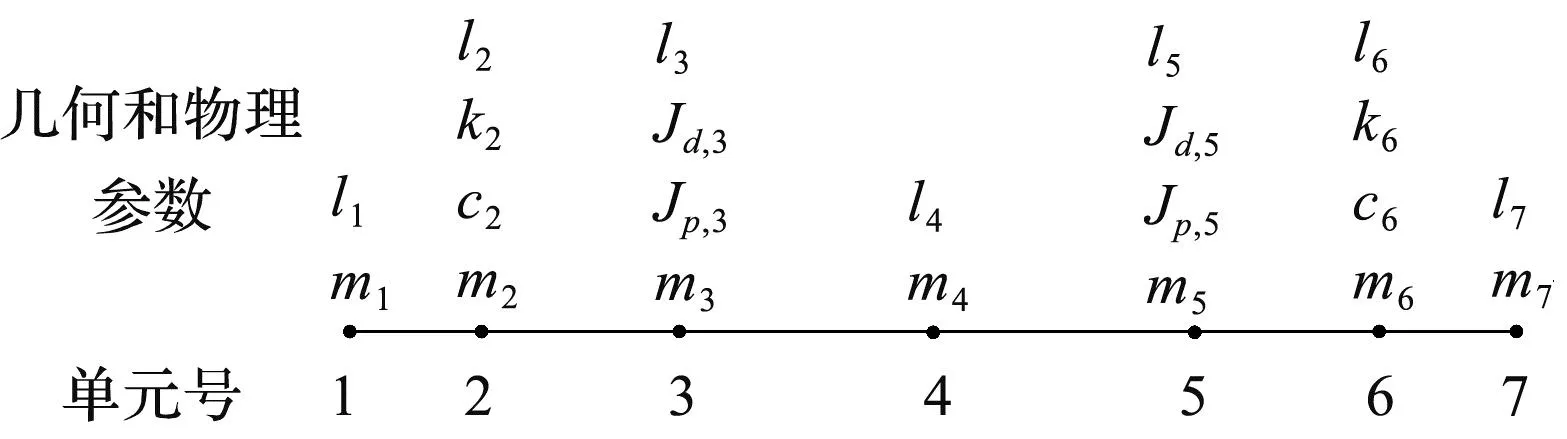
图2 转子-支承系统计算模型

根据图2所示的计算模型,可得其确定性动力学计算模型:

(1)

(2)

其中:

(3)

(4)

(5)

(6)

1.2 确定性动力学降阶模型

动力学模型的降阶能够缩短系统动力学特性的计算时间,其本质是对动力学模型的自由度数进行减缩。

式(1)所示动力学模型对应的齐次式如下:

(7)

(8)

(9)

(10)

(11)

如果不计惯性力对副自由度的影响,则考虑自由振动时,式(11)可简化为:

(12)

由此可得副自由度位移向量为:

(13)

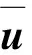
(14)

(15)

(16)

(17)

(18)

(19)

(20)

综合式(8)～式(20)可得转子系统确定性动力学降阶模型为:

(21)

1.3 不确定动力学降阶模型

设Bd为n阶满秩实数矩阵,对应的随机矩阵记为Br,且Bd和Br满足:

Bd=E(Br)

(22)

式中:E(Br)为求随机矩阵Br的均值矩阵。

对矩阵Bd进行极分解,则有:

Bd=H2U

(23)

式中:U为正交矩阵;H2为正定矩阵。

由于满秩实数矩阵极分解的极因子矩阵是唯一存在的,因此可用左极分解的方法构造随机矩阵Br,即:

Br=HBrUBr

(24)

对Br进行奇异值分解,可推导出矩阵HBr和UBr为:

(25)

根据式(23)～式(25),可将转子系统的不对称刚度矩阵及阻尼矩阵表示为:

Kr=HKrUKr

(26)

式中:HKr为随机矩阵。

Cr=HCrUCr

(27)

根据文献[24]的非参数动力学建模方法,式(26)中HKr为随机矩阵,且满足:

(28)

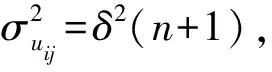
利用Hd和G的上三角因子矩阵可计算出HKr和HCr,再将结果代入式(26)和式(27)中,便得到不确定刚度矩阵Kr和不确定阻尼矩阵Cr:

(29)

(30)

(31)

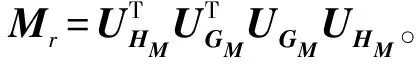
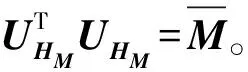
2 模型散度参数辨识方法

在第1.3节中,笔者构建了转子系统的不确定转子-支承系统的动力学模型,但模型中的散度参数是未知的。

根据文献[25]的方法,利用实验得到的振型矩阵Ψ和确定性动力学模型的振型矩阵φ可对不确定动力学降阶模型中的散度参数进行辨识。

假设u为实验得到的广义坐标列向量,ud为确定性动力学计算模型的广义坐标列向量,则有:

Ψu=φud

(32)

(33)

(34)

3 辨识方法的实验验证

3.1 实验步骤

为了验证散度参数辨识方法的有效性,笔者在转子实验平台上进行实验验证。

转子实验台实物图如图3所示。

图3 转子实验台

实验分为三个步骤:1)对图3的转子系统进行确定性动力学建模,并计算出其最低阶临界转速和主振型;2)利用第2节的方法估算出散度参数的数值;3)采用第1节的方法建立的不确定系统非参数动力学计算模型,计算出3 800 r/min以内的不平衡位移响应结果,并将其和确定性动力学模型所计算的振动响应进行对比分析。

转子实验台参数如表1所示。

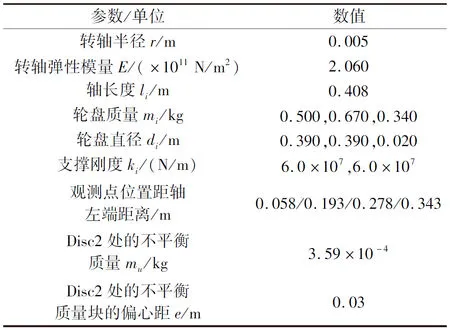
表1 转子实验台参数

3.2 估算散度参数

利用确定性动力学模型可以得到转子系统的坎贝尔图,如图4所示。

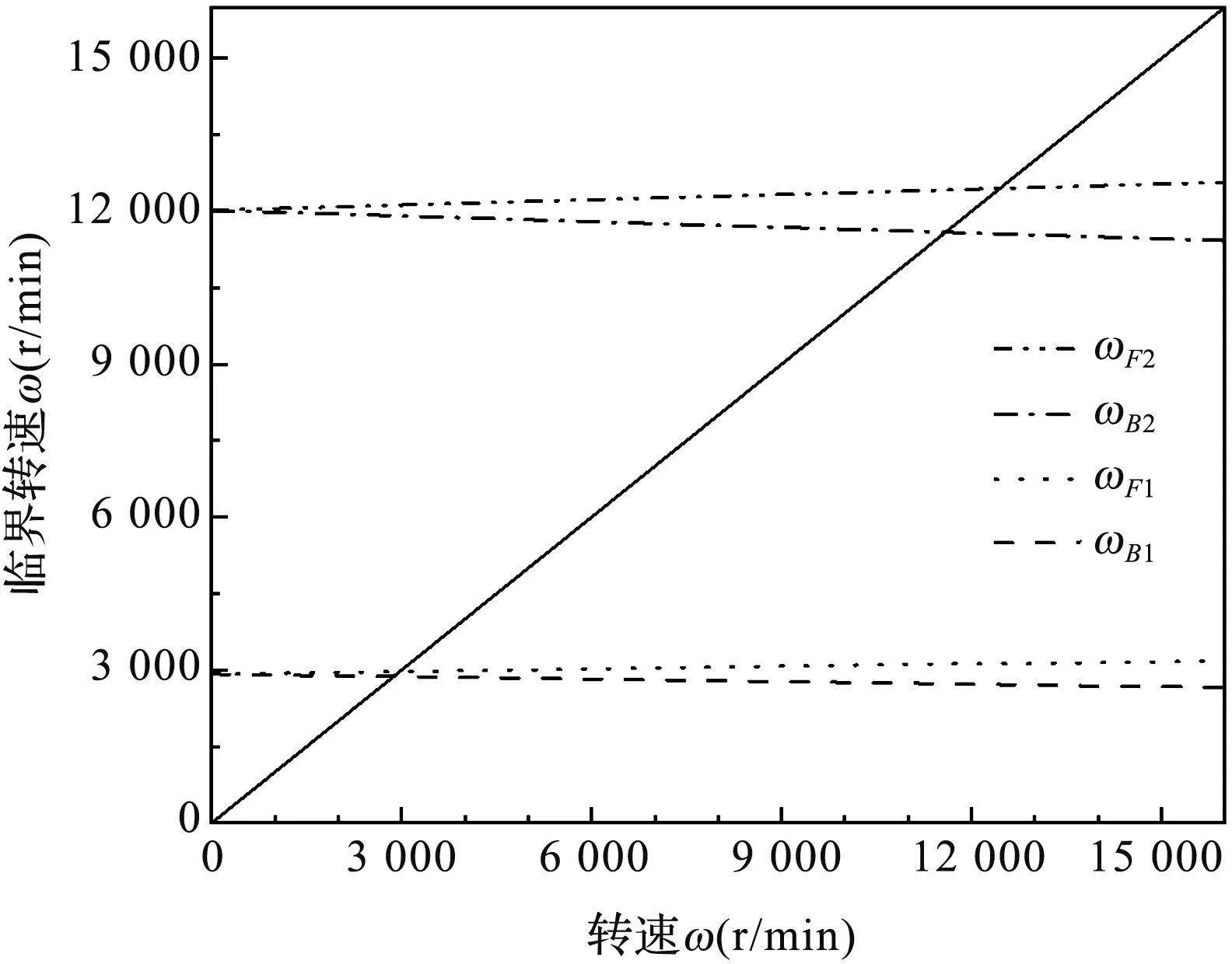
图4 确定性动力学计算模型Campbell图

由图4可知,确定性系统的一阶反、正进动临界转速分别为ωBc1=2 872 r/min和ωFc1=2 967 r/min。

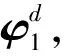
图5 确定性动力学计算模型的一阶振型

转子系统一阶振型如图6所示。

图6 转子系统一阶振型

S=(ψTψ)-1ψTφ

(35)

将矩阵S代入式(33)～式(34),估算出的散度参数为δM=0.018 4,δK=0.130 9。

3.3 散度参数辨识结果的实验验证

笔者将图3所示的转子系统划分为20个节点,利用1.2节降阶方法将节点数减缩为11个,采用第1节的非参数动力学降阶计算模型和第3.2节的散度参数识别结果,预测在3 500 r/min转速范围内4个位置处的振动位移响应结果,对实验数据与预测结果进行比较和分析。

实验结果与非参数不确定动力学计算模型预测结果对比如图7所示。

图7 振动响应实测结果与非参数动力学模型预测的对比

图7实验结果表明:在转速范围3 000 r/min内,实验测出的振动响应曲线、确定性计算模型和非参数不确定动力学计算模型所得到的振动响应曲线几乎重合。但是在3 000 r/min～3 800 r/min转速区间时,非参数动力学计算模型的预测均值曲线相比确定性动力学计算模型更接近实际振动响应曲线。

在转速时:

在位置1处,确定性和不确定性动力学振动响应幅值分别为2.17×10-4m和1.55×10-4m,与实测结果1.72×10-4m相比分别相差26.47%和10.21%,与确定性模型相比,非参数模型的预测结果更接近实际结果。

在位置2处,两种计算模型的振动响应幅值分别为3.69×10-4m和2.67×10-4m,与实际结果2.96×10-4m相比分别相差24.66%和9.79%。

在位置3处,两种计算模型的振动响应幅值分别为2.95×10-4m和2.11×10-4m,与实际结果2.39×10-4m相比分别相差23.43%和11.71%。

在位置4处,两种计算模型的振动响应幅值分别为7.61×10-4m和5.45×10-4m,与实际结果6.22×10-4m相比分别相差22.34%和12.37%。

根据以上四个位置的振动响应实验对比可知:非参数动力学模型的均值计算结果与实际结果更相近,表示第一节提出的模型比转子系统确定性模型更合理;并且,在散度参数计算中得到的散度参数δM=0.018 4,δK=0.130 9也相对合理。

4 结束语

针对不确定性转子系统,基于随机矩阵理论和非参数动力学建模方法,笔者构建了模型不确定性动力学降阶计算模型;利用系统确定性模型的一阶临界转速、振型和实验数据,对动力学模型的散度参数进行了辨识;并在转子实验台上对散度参数辨识结果进行了实验验证。

研究结果表明:

1)将非参数建模与矩阵极分解方法相融合,并进行静态矩阵降阶,可以建立具有模型不确定性的转子系统动力学计算模型;

2)转速在3 000 r/min范围内时,由确定性动力学模型和不确定动力学模型得到的振动响应均与实际结果接近;转速在3 000 r/min～3 800 r/min范围时,不确定动力学计算模型的均值计算结果比确定性动力学模型更接近实际结果。表明在转子模型中考虑模型不确定性更加合理。

在后续的研究工作中,笔者拟将动态矩阵降阶方法应用于模型不确定性转子系统中。