基于RBF神经网络整定PID的电液比例系统位置控制研究*

陈翰文,徐巧玉*,徐 恺,张 正

(1.河南科技大学 机电工程学院,河南 洛阳 471000;2.洛阳银杏科技有限公司,河南 洛阳 471000)

0 引 言

随着我国隧道工程建设速度高速增长,凿岩机械臂被广泛应用于隧道钻爆工程中。其中,凿岩机械臂的电液比例位置控制系统是机械臂运动控制的基础,同时电液比例控制受外部干扰、油温和黏度变化的影响很大,影响机械臂末端钻孔点的位置精度[1-5]。因此,为了提高凿岩施工作业的效率和精度,亟需解决电液比例系统位置控制精度的问题。

由于PID控制算法简单、鲁棒性强、易于实现,以及能够与多种智能算法相结合提升适应性能力的优势,被广泛应用于电液比例系统控制领域[6-9]。

万海兵[10]提出了一种非线性函数构造PID控制器的方法,对电液比例系统进行了开环位置控制,其提高了系统的响应速度,减小了超调量。YI Ye等人[11]利用改进的粒子群优化算法提高了PID参数的搜索效率,通过仿真实验验证了该算法对电液比例系统位置控制的跟踪效果。罗艳蕾等人[12]基于模糊PID控制对电液比例位置控制系统进行了仿真研究,结果表明该方法有效地提高了系统的响应速度和位置跟踪能力。赵怡麟[13]将具有自适应能力的单神经元PID算法用于电液比例系统的闭环位置控制,有效改善了系统的控制性能。

因此,为满足不同工况下的电液比例系统控制需求,选用自适应能力强、抗干扰性能好的控制算法来快速、准确地整定PID参数是解决电液比例系统位置控制精度问题的关键。

针对上述问题,笔者提出基于径向基函数(radical basis function,RBF)神经网络整定PID参数的控制算法,在MATLAB/Simulink下搭建系统闭环控制结构图,使用MATLAB函数模块编写程序,完成RBF神经网络整定PID控制算法的任务;在AMESim中搭建电液比例系统模型,进行联合仿真;根据电液系统运行的状态,RBF神经网络可在线自学习整定PID控制器的参数,提高电液比例系统位置控制精度。

1 凿岩机械臂电液比例位置控制系统

笔者选取全自动凿岩台车机械臂作为研究对象。凿岩机械臂在进行钻孔工作中,机械臂末端到达目标孔位置需要对7个关节对应的电液系统分别进行位置控制。

此处笔者以大臂摆动的电液比例系统位置控制为例进行分析建模,其余各个关节控制系统可以以此类推,不进行详细叙述[14]。

1.1 电液比例系统位置控制原理

电液系统是由电机、液压泵、安全阀、电液比例换向阀、带负载油缸和位移传感器等组成。电液系统是一个十分复杂的非线性控制系统,为了进行控制算法的仿真研究,通常采用电液系统建模,其是对电液系统各个环节进行分析和搭建数学模型。

笔者预先测量液压缸面积及系统压力,按照工作过程中的要求核算液压缸及系统的流量、压力和固有频率,选择电液比例阀的规格参数和比例放大器的设计;对比例放大器、电液比例阀、液压缸和位移传感器的工作原理和结构参数进行分析,考虑油缸和油路的泄漏系数,从而对系统各模块进行机理建模,确定电液比例系统各部分的传递函数[15-17]。

凿岩台车机械臂整体液压原理图如图1所示。

图1 凿岩机械臂整体液压原理图

具体控制实现流程为:根据给定目标炮孔位姿信息,求出液压缸活塞杆伸缩量Y1;通过模数转化成相应的电压控制信号U1,由位移传感器测出的实时反馈位置信号Y2转换成与之成比例的电流U2后输送到控制器,与输入电流U1比较后计算偏差值e=U1-U2;控制系统利用控制算法根据偏差量得出控制电流值U,再通过比例放大器转换成相应的电流信号I,其控制电液比例阀的开度和阀芯位移;泵输出的流量按输入的电信号控制阀的开度成比例地变化,推动液压活塞杆产生相应的位移。

电液比例位置系统常规控制设计流程图如图2所示。

图2 电液比例位置系统设计流程

1.2 电液比例系统AMESim建模

为了快速建立液压系统的数学模型,笔者对复杂的电液比例系统进行了建模和仿真分析。借助AMESim软件,在AMESim中搭建了电液比例系统的仿真模型,避免了建立阀控非对称液压缸控制系统的数学模型和推导传递函数,采用这种方法可以使系统仿真工作量大大减少。

在AMESim中搭建电液比例系统仿真模型流程如下:

1)创建新模型。打开AMESim软件,点击“新建”按钮,选择“空白工程”创建新模型,定义系统的基本组成部分及相互关系,如各种传感器、执行器和控制器等;

2)添加元件。在工具栏中选择“液压与气控”分类下的元件,添加电机、液压泵、溢流阀、液压缸、电液比例换向阀、位移传感器等元件,连接它们的液压管路和电气线路;

3)配置元件参数。打开每个元件的属性窗口,配置相应的参数,例如液压泵的功率、压力和流量;液压缸的压力、面积和活塞杆直径;电液比例阀的阀门开度和额定电流等;

4)定义信号。需要定义输入信号,如对于电液比例阀,需要定义控制信号,可以选择手动设置阀门开度,也可以通过输入电流信号来控制;

5)运行仿真。完成模型搭建和参数配置之后,点击“仿真”按钮即可运行仿真,并观察系统的动态响应和各元件的工作状态,如液压泵的转速和流量、液压缸的运动速度和力等;

6)分析结果。基于构建的系统模型和设置的工作条件,进行仿真分析和参数优化以评估系统的性能和可靠性,通过仿真结果,可以了解系统的性能和稳定性,如油缸输出流量、位置精度等。

由上述过程,笔者可以在AMESim中搭建单个关节的未加控制算法的电液比例系统位置控制的简化模型。电液比例位置系统仿真模型如图3所示。

图3 AMESim电液系统仿真模型

电液系统采用电机、定量泵和作为安全阀的溢流阀组成定压供油单元,以电液比例换向阀为控制元件,单杆双作用液压缸作为执行元件。通过位移传感器实时反馈液压缸的位移变化量,笔者将反馈的位移变化量与给定液压缸预期位移变化比较得出偏差量。偏差量与外加输入信号通过控制算法实现电液换向阀的开度控制目的,进而控制液压缸内推动活塞杆运动的液压油流量大小,进行液压缸活塞杆的位置控制以及负载机械臂各关节的驱动动作。

2 RBF神经网络PID控制器设计

2.1 RBF网络结构

RBF网络是一种三层的前馈式神经网络,由输入到输出的映射是非线性的;而隐含层空间到输出空间的映射是线性的,从而大大加快了学习速度并避免局部极小问题。

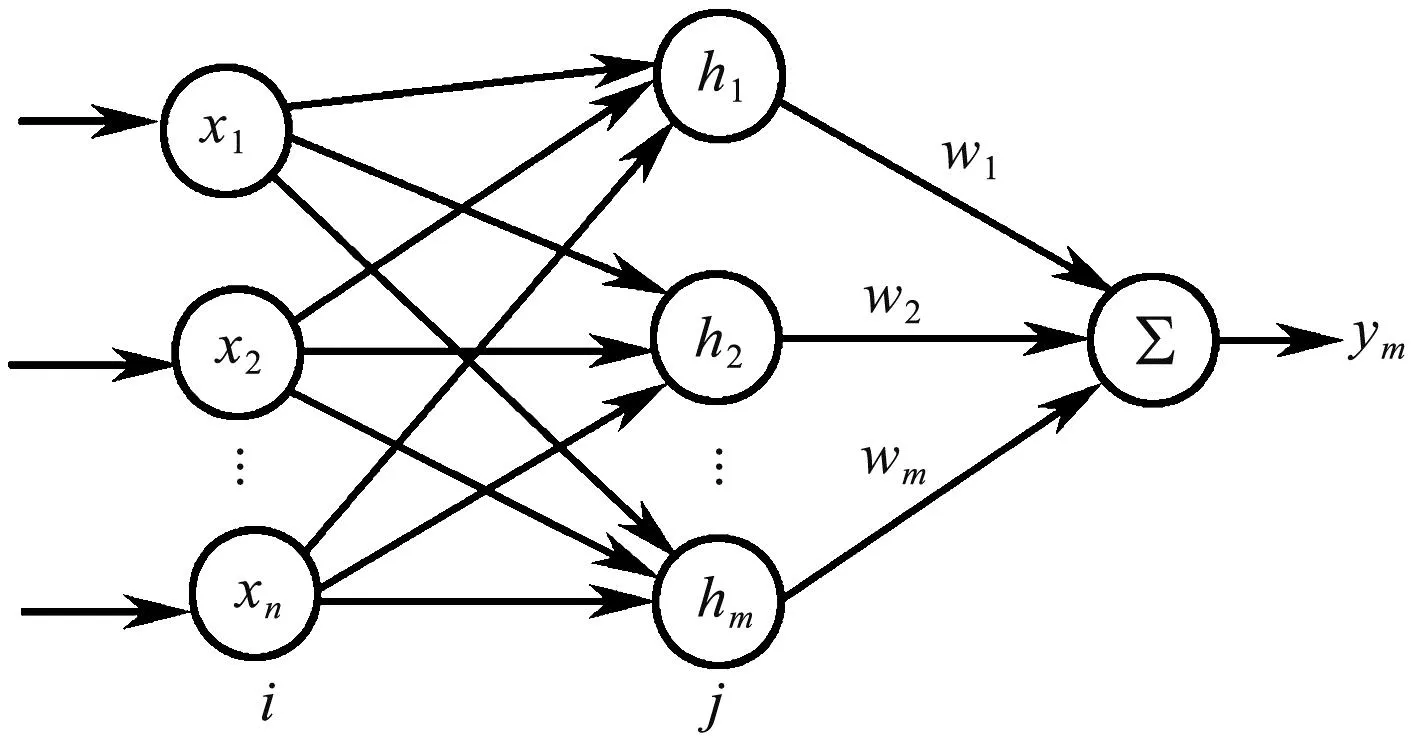
图4 RBF神经网络结构

2.2 被控对象Jacobian信息辨识算法

在RBF网络结构中,网络的输入向量X=[x1,x2,…,xn]T。设RBF网络的径向基向量H=[h1,h2,…,hj,…,hm]T,网络隐藏节点的基宽向量为B=[b1,b2,…,bj,…,bm]T,则高斯基函数为:

(1)

式中:Cj为网络的第个隐藏节点的中心矢量,Cj=[Cj1,Cj2,…,Cji,…,Cjn]T,i=1,2,…,n;bj为节点j的基宽度参数,且为大于零的数。

辨识网络的输出ym(k)为:

ym(k)=w1h1+w2h2+Λ+wmhm

(2)

式中:W为网络的权向量,W=[w1,w2,…,wj,…wm]T。

辨识器的性能指标函数为:

(3)

式中:yout(k)为时刻被控系统的输出值;yn(k)为k时刻RBF网络的输出值。

根据梯度下降法,输出权wi、节点中心cji及节点基宽bj各参数的迭代算法如下所示:

输出权为:

罗恬听到“噗”的一声，像刺进了一团皮革。她惊恐地抬起头，发觉杜朗并没有疼痛的表情。罗恬这才松了口气，拔出匕首说：“太不可思议了，你是怎么做到的？”

wj(k)=wj(k-1)+η(yout(k)-ym(k))hj+

α(wj(k-1)-wj(k-2))+β(wj(k-2)-wj(k-3))

(4)

节点中心变化量Δcji为:

(5)

节点中心cji为:

cji(k)=cji(k-1)+ηΔcji+α(cji(k-1)-

cji(k-2))+β(cji(k-2)-cji(k-3))

(6)

节点基宽变化量为:

(7)

节点基宽参数bj为:

bj(k)=bj(k-1)+ηΔbj+α(bj(k-1)-

bj(k-2))+β(bj(k-2)-bj(k-3))

(8)

式中:η为学习效率;α,β为动量因子。

Jacobian阵(对象的输出对控制输入变化的灵敏度信息)算法如下所示:

(9)

式中:y(k)为时刻被控系统的输出值;Δu(k)为第k次采样时刻的控制增量,x1=Δu(k)。

2.3 RBF网络PID整定原理

笔者采用增量式PID控制器,rin(k)为时刻被控系统的输入值,yout(k)为时刻被控系统的输出值,控制误差为:

error(k)=rin(k)-yout(k)

(10)

PID三项输入为:

xc(1)=error(k)-error(k-1)

(11)

xc(2)=error(k)

(12)

xc(3)=error(k)-2error(k-1)+error(k-2)

(13)

控制算法为:

u(k)=u(k-1)+Δu(k)

(14)

Δu(k)=kpxc(1)+kixc(2)+kdxc(3)

(15)

神经网络整定标准为:

(16)

其中kp,ki,kd的调整采用梯度下降法:

(17)

(18)

(19)

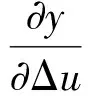
RBF整定PID控制系统的结构如图5所示。

图5 RBF网络整定PID控制框图

2.4 RBF-PID控制器仿真实现

RBF神经网络结构:3-6-1,网络辨识的3个输入分别为:Δu(k),yout(k),yout(k-1)。网络输出为:ymout(k);数据节点基函数中心向量初值ci:30×ones(3,6);数据节点基宽初值bi:40×ones(6,1);输出层权重w:10×ones(6,1);网络的学习效率:xite=0.5;PID各项参数学习效率:xitekp=0.2,xiteki=0.2,xitekd=0.2;kp、ki、kd的初值为:10、0.55、2;动量因子,alfa=0.05,bete=0.01。系统输入选择单位阶跃信号、多段阶跃位移信号和正弦位移信号。

笔者在Simulink下搭建系统闭环控制框图,在MATLABFunction中编写RBF神经网络整定PID的算法程序,实现RBF在线自整定PID控制功能。

总体算法实现步骤如下:

1)根据Simulink搭建的仿真模型得出系统输入rin(k),系统输出yout(k),并实时计算误差值e(k);

2)设置MATLAB Function输入与输出接口,输入接口为实时反馈的误差值e(k)和系统输出值yout(k),输出接口为不断更新输出的Kp,Ki,Kd参数值和控制器输出值u(k),编写程序构造网络结构,初始化上述各参数;

3)根据RBF神经网络算法计算RBF辨识器的输出,并根据辨识器的性能指标函数和实时反馈的参数值,不断修正数据节点基函数中心向量ci、节点基宽bi、输出层权重系数w,并计算被控对象的Jacobian值;

4)PID控制器采用增量式PID控制方法,根据实时反馈的误差值e(k)和Jacobian值,可不断调整PID控制器中Kp,Ki,Kd值,计算出PID控制器的u(k)值,更新被控对象输出;

5)返回步骤2)循环进行,不断重复上述过程,更新各项参数数值,直到采样时间结束为止。

RBF神经网络PID控制器Simulink模型如图6所示。

图6 RBF神经网络PID控制器Simulink模型

3 电液比例位置系统控制联合仿真

3.1 Simulink联合AMESim仿真

对于电液比例系统这样复杂的非线性控制系统,笔者将AMESim构造的电液比例系统物理模型和在MATLAB/Simulink中完成的RBF神经网络PID控制器进行联合仿真。

由文献[18-22]可知,联合仿真可以进行电液系统和控制系统之间的耦合,从而完成对整个系统的仿真分析任务,便于进行控制策略的优化和测试。

联合仿真的目的是加入控制算法,控制电液比例阀的开度大小及输出流量,进而控制液压缸活塞杆的位移。

联合仿真流程如下:

1)在MATLAB/Simulink中建立RBF神经网络PID控制系统模型,在AMESim中创建电液比例系统的物理系统模型。用AMESim与MATLAB/Simulink联合仿真工具,在AMESim界面打开接口功能,点击创建联仿接口,选择SimCosim,定义输入、输出接口数量,建立2个模型之间的连接;

2)保存AMESim仿真模型文件,并设置名称为RBF329,接着在AMESim界面运行仿真,点击Simulink按键,可直接打开MATLAB/Simulink;

3)在Simulink界面创建S-function模块,将S-function名称设置为与AMESim搭建的仿真模型文件名称一致,并在名称末尾加下划线,如RBF329_,设置S函数参数分别为0.01,0.001,1.00×10-5,点击仿真按钮,仿真结束即可完成联合仿真任务;

4)启动仿真后,Simulink将数据信号传递到AMESim中的模型,可同时在Simulink仿真界面和AMESim仿真界面查看仿真结果。

笔者在AMESim下创建了联仿接口,搭建了阀控非对称液压缸的电液系统联合仿真模型,如图7所示。

图7 AMESim联合仿真模型

在AMESim中创建联仿接口模块的作用是为了将电液系统模型导入进MATLAB中。该接口模块的输入端是液压油缸活塞杆的位移信号,输出端为电液比例阀的控制电流信号。在MATLAB/Simulink中创建的S-function模块是为了运行电液系统的物理模型,该模块的输入端为电液比例阀的控制电流信号,输出端为油缸活塞杆的位移信号。使用联合仿真接口实现了AMESim与Simulink之间电液系统的控制和位移信号相互传递的目的。

在MATLAB/Simulink下搭建的联合仿真模型如图8所示。

图8 Simulink实现RBF-PID联合仿真模型

被控对象为在AMESim中搭建的电液系统模型,控制算法为RBF神经网络整定PID控制算法,输入信号为阶跃信号、多段阶跃位移信号和正弦位移信号。

在整个仿真过程中,笔者将检测到的油缸活塞杆位移信号作为反馈信号,将反馈信号与输入的期望信号差值作为控制系统的一项输入;利用控制器计算得出电液比例阀的控制量u,将其输入到S-function模块,驱动电液比例阀工作,进而驱动油缸活塞杆进行运动,产生位移量再反馈回去,反复循环,最终实现电液比例系统的位置控制功能。

为了将RBF网络整定PID的效果和常规PID的效果进行对比,笔者搭建了常规PID控制电液系统的模型;在常规PID参数调整过程中,采用试凑法,先调Kp,使Ki、Kd值为0,观察系统响应,如果系统超调量大,可以通过增加Ki值的同时减小Kp值;最后根据系统的动态特性调整Kd,再使Kp由小往大调节。

笔者按照这种调节方式通过多次试凑,确定Kp=28,Ki=0.01,Kd=1.8。采样时间间隔为0.01 s。

使用常规PID控制的电液系统在MATLAB/Simulink中联合仿真模型,如图9所示。

图9 Simulink实现常规PID联合仿真模型

3.2 仿真结果

在AMESim参数模式下,笔者设置了电液比例系统模块的参数,如表1所示。

表1 电液比例系统模块参数

为了验证RBF神经网络PID控制器控制电液比例位置系统的性能,笔者使用RBF神经网络整定PID控制器和常规PID控制器,分别输入不同的目标位移信号进行仿真分析。

阶跃位移信号响应的仿真结果如图10所示。

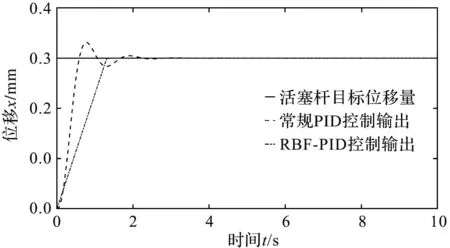
图10 活塞杆阶跃位移信号响应

由图10可知:在阶跃位移信号下的电液系统位置控制中,常规PID方法控制到达目标位置时间约为3 s,且存在超调量;而RBF整定PID方法控制上升时间约为1.4 s,系统响应快速且无超调。

外部干扰的阶跃位移信号响应的仿真结果如图11所示。

图11 外加干扰活塞杆阶跃位移信号响应

由图11可知:在5 s时添加5 000 N的外部干扰力,常规PID方法控制系统输出位移在目标位置附近多次波动,需要2 s才能恢复至目标位置保持稳定;而RBF整定PID控制系统输出位移在目标位置-0.025 m～0.025 m之间发生波动,然后在0.3 s内恢复至目标位置并保持稳定。这说明RBF神经网络整定PID有较好的抗干扰性能。

多段阶跃位移信号响应的仿真结果如图12所示。

图12 活塞杆多段阶跃位移信号响应

由图12可知:设计输入多段活塞杆运行目标位置信号,常规PID控制油缸活塞杆各阶段平均调节时间为3 s;而RBF神经网络整定PID控制油缸活塞杆各阶段平均调节时间为1.5 s,系统运行平稳快速、无超调。

正弦位移信号响应的仿真结果如图13所示。

图13 活塞杆正弦位移信号响应

由图13可知:因为在AMESim下搭建的液压缸活塞杆有效行程为0 m～0.673 m,所以只采用正值的正弦信号进行跟踪响应,在整个位置控制过程中,常规PID整体位置控制效果不佳,最大误差达到了20 mm;而RBF整定PID控制整体位置控制最大误差不超过5 mm。

多段阶跃位移信号下RBF神经网络整定Kp、Ki、Kd参数结果如图14所示。

图14 多段阶跃位移信号下RBF整定PID

由图14知可:当系统输入活塞杆多段阶跃位移信号变化时,Kp值在10～10.5之间变化,Ki值在0.55～0.66之间变化,Kd值在2～2.16之间变化。

再进行参数整定,当系统误差为0,即系统稳定时,PID参数会保持稳定。

4 实验验证及分析

4.1 实验平台

为验证凿岩台车机械臂电液比例系统位置控制算法的实际控制效果,笔者以某单位设计制造的G3ZI型凿岩台车机械臂为实验对象,进行现场实验验证。笔者搭建的电液系统位置控制实验平台主要由实验对象、液压系统、电气控制系统等组成。

凿岩台车机械臂实物图如图15所示。

图15 G3ZI凿岩台车及其机械臂

凿岩台车机械臂的液压系统主要由HLPSV型多路电液比例换向阀、液压泵及油管组成。整个液压系统由液压泵不断地提供动力来源,电气控制系统可以根据给定目标信号自动开启并控制多路电液比例换向阀的阀口开度;操作人员也可以手动操作手柄,控制多路电液比例换向阀的开度。两种操作方式都可以控制换向阀输出液压油驱动油缸活塞杆运动,从而控制机械臂进行各种动作。

多路电液比例换向阀如图16所示。

图16 HLPSV型多路电液比例换向阀

凿岩台车机械臂电气控制电路板如图17所示。

图17 电气控制电路板

凿岩台车机械臂电气控制系统主要进行机械臂关节各项数据的传输与计算,通过将RBF神经网络整定PID和常规PID控制算法以嵌入式的方式下载进主控芯片中,将其转换成相应的电信号,控制电液比例阀的阀口开口大小,从而对机械臂进行运动控制。

4.2 实验测试与结果分析

笔者以大臂左油缸活塞杆伸缩位置控制为例,设计RBF神经网络整定PID控制器和常规PID控制器,进行实验验证。

根据末端打孔位置信息,确定大臂摆动关节变量,从而确定大臂左油缸活塞杆伸缩位置。预先计算5组油缸活塞杆理论伸缩位置值,为避免上一组的活塞杆位置误差对下一组位置控制造成影响,当每一组油缸活塞杆停止运动后,手动调节换向阀,使活塞杆运行至该组的理论位置。测量油缸活塞杆伸缩为0时和每组实验油缸活塞杆停止运动时,其分别处在油缸外的长度,可以求出每组活塞杆实际伸缩值。利用秒表粗略记录活塞杆从上一组位置运行至下一组位置的响应时间,最终得到2种方法控制大臂左油缸活塞杆位置误差与响应时间。

活塞杆位置控制实验结果如表2所示。

表2 活塞杆位置控制实验结果

由表2数据可知:通过实验验证,常规PID控制大臂左油缸活塞杆位置平均误差为10.32 mm,实验全程总响应时间约为8.5 s;RBF神经网络整定PID控制大臂左油缸活塞杆位置平均误差为2.6 mm,实验全程总响应时间约为5.5 s。

综上所述,在凿岩台车机械臂电液比例控制系统中,相较于常规PID控制方式,RBF神经网络整定PID算法响应时间更快,控制活塞杆位置精度误差降低了75%,并具有良好的抗干扰性能。

由此可见,相比于常规PID控制,RBF整定PID电液系统响应更加快速,具有更好的位置精度控制效果,可以有效提高电液比例系统的位置控制精度。

5 结束语

笔者提出了一种基于RBF神经网络整定PID的电液比例系统位置控制方法,在MATLAB/Simulink中搭建了系统闭环控制结构图,不断更新RBF网络参数整定PID控制算法,与在AMESim中搭建的电液比例系统的简化模型进行了联合仿真,完成了整个控制系统的全面仿真和分析任务;同时对实际凿岩台车机械臂进行了电液比例位置控制实验验证。

仿真与实验结果如下:

1)联合仿真的结果表明,在MATLAB Function下,通过编写算法程序建立的RBF神经网络整定PID控制器,能够实时在线调整PID控制器的3个参数,可以有效提高电液比例系统的响应速度和位置精度;

2)相较于常规PID控制方式,RBF神经网络整定PID算法的响应更加快速、抗干扰能力更强、控制活塞杆位置精度误差不超过5 mm;实际施工中凿岩机械臂电液系统对位置精度的误差范围要求在10 mm以内,因此RBF神经网络整定PID控制方法满足凿岩机械臂实际工作中对电液比例系统位置精度的控制要求,可以应用于工业生产实际中。

后续,笔者将继续深入开展电液比例位置控制系统的实验和仿真研究,以揭示系统的动态性能变化规律,优化系统设计和控制策略。