多马尔可夫链协同的航班客舱保障过程预测

邢志伟，刘 鹏+，李 彪，罗 谦

(1.中国民航大学 电子信息与自动化学院，天津 300300；2.中国民用航空局第二研究所 工程技术研究中心，四川 成都 610041)

0 引 言

机场作为民航运输环节的关键节点，在保障安全的前提下应尽可能提高机场地面运行的效率和质量。航班在泊入机位后要开展各项客舱保障，其过程预测的准确性很大程度影响了机场推出时隙及保障资源的分配，实现航班客舱保障环节的精确动态预测，为机场运行精细化管理提供决策依据进而提升机场智慧化[1]运营能力。

客舱保障指航班从下客开始到撤轮挡之前以飞机客舱为核心的服务过程，是航班地面保障过程的核心组成部分。目前国内外的研究成果主要集中在地面保障过程的仿真分析[2，3]、流程优化[4，5]以及服务时间估计[6，7]等，而单独针对客舱保障过程每一节点发生时刻的研究极少涉及。王立文等[8]在充分考虑航班运行属性的基础上，基于贝叶斯网络实现了地面保障关键节点的动态预测，但是对于客舱保障过程刻画不详细。Q Luo等[9]为实现机场运行协同，提出了基于Petri网的地面保障过程态势感知方法，但未对保障细节做详细论证。C Liu等[10]从航班地面服务网络出发，在滑动窗口变化点检测的动态网络模型推理框架的基础上实现了变化节点检测。Jenaro Nosedal等[11]通过对机场周转过程分析，利用因果方法对影响航班保障过程的不同扰动开展了定时评估。邢志伟等[12]考虑了服务流程的复杂性和特殊性，建立了基于深度神经网络的航班地面保障预测模型，虽能够较为精确地预测航班保障时间，但无法描述保障过程的细节问题。

对于上述问题，本文从过站航班客舱保障过程分析出发，构建其网络拓补图的马尔可夫模型，设计面向航班客舱保障过程的DBSCAN-SMMC预测方法，基于某机场的历史保障节点数据仿真验证，实现客舱保障每一节点的实时预测。

1 航班客舱保障过程分析与建模

1.1 过程分析

客舱保障是航班过站时地面保障过程中的重要环节之一，主要包括航班离港前为保障接续航班正常运行而针对客舱的一系列服务，分为加餐食、客舱清洁、垃圾处理、加清水、排污水5个子过程。在机场，客舱保障过程没有明确的开始和结束时间，保障环节任一过程最先开始作业，即视为客舱保障过程开始，所有环节作业结束，则该过程结束，客舱保障过程如图1所示。在实际运行中，配餐作业结束后才会开始排污水作业，而配餐过程和排污水作业均可与加清水作业并行工作，在下客结束后即可开始客舱清洁工作，期间垃圾车作业，在客舱清洁结束后，垃圾车作业随之完成。为直观描述客舱保障各个环节之间的约束关系，将航班客舱保障过程刻画为如图2所示的甘特图。整个过程必须严格遵守机场的地面运行标准，如果某个航班的某个客舱保障环节出现问题，不仅会影响当前航班的飞行计划，还有可能造成一系列航班保障不及时引发的机场大面积延误。综上，客舱保障过程是一个多条件约束、多资源协同、具有严格时间窗的复杂过程。

图1 过站航班客舱保障过程

图2 过站航班客舱保障过程甘特图

针对单个航班客舱保障过程的资源协同预测开展分析与建模，对实际流程做如下理想化处理：

(1)由于始发航班接受保障的时间窗较为宽裕，终到航班不会影响后续航班的执行，且保障过程不完整，因此只考虑过站航班的客舱保障过程。

(2)实际保障过程中，机型大小和执行航线的不同都会影响保障资源的供应量，视为餐食车能一次性提供航班的需求量，清水车、污水车、垃圾车只开展一次作业即可完成本航班的保障，同时不考虑极少数不需要完整保障过程的过站航班。

(3)忽略保障资源的调度对客舱保障过程造成的影响。

(4)实际保障过程中，下客结束和客舱清洁开始两个节点具有短时连续性和同步性，即下客结束后紧接着就开始客舱清洁，所以将两个节点视为同一过程。

1.2 航班客舱保障过程马尔可夫模型

马尔可夫链(Markov chain)为状态空间中从一个状态到另一个状态的转换的随机过程，该过程的特点是无后效性，即下一个状态的概率分布只能由当前状态决定。作为描述随机事件因果关系的重要方法之一，在移动对象轨迹预测、销量预测、故障预测[13-17]等方面具有广泛的应用。

航班客舱保障过程预测问题可以表示为：已知某保障过程节点时间的变化轨迹 {T(xk)|k=1，2，3，…xk表示保障节点} 和轨迹预测模型，求解第k+1个节点的时刻T(xk+1)。因每一保障节点的时间只与前一节点有关，因此将此问题视为一个马尔可夫过程，并由马尔可夫链来表示。选取与客舱保障过程相关联的节点，将客舱保障过程结构图等效为如图3所示的网络拓补。

图3 客舱保障过程网络拓补

其中，x1表示下客开始，x2表示下客结束，x3表示清水车作业开始，x4表示清水车作业结束，x5表示配餐开始，x6表示配餐结束，x7表示污水车作业开始，x8表示污水车作业结束，x9表示客舱清洁开始，x10表示垃圾车作业开始，x11表示客舱清洁结束，x12垃圾车作业结束，x13是一个虚拟的节点，表示客舱保障过程结束。

由于x13是一个虚拟的节点，不影响预测过程，x2与x9具有同步性，在预测过程等效为一个节点，用x9来表示。所以图3的网络拓补结构看作3个并行的过程，只要x1发生，3个过程均已开始且互不影响，将其等效为3条马尔可夫链，如图4所示。

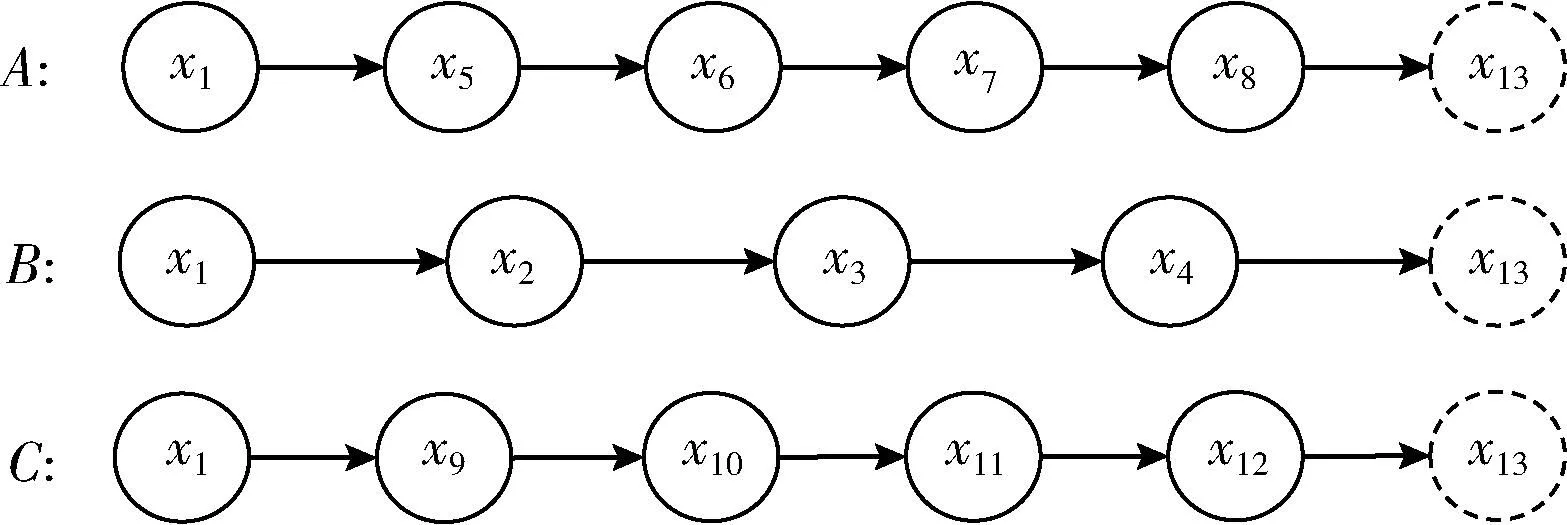
图4 等效马尔可夫链

定义1 马尔可夫性：航班客舱保障过程马尔可夫性可以被定义为

P(Xl+1=tj|X1=t1，X2=t2，…，Xl=ti)=

P(Xl+1=tj|Xl=ti)

(1)

式中：{Xl，l=1，2，…} 为该马尔可夫链的随机序列，表示航班客舱保障流程中节点的集合，l表示马尔可夫链中xk的位置，k=1，2，…，13；T={t1，t2，…，ti-1，ti，tj…} 为状态空间，表示保障节点的状态时刻值的集合。Xl表示当前发生的保障节点，Xl+1表示即将发生的保障节点，ti为当前保障节点的时刻状态，tj为即将发生的保障节点的时刻状态预测。

定义2 转移概率：航班客舱保障过程马尔可夫链为X={X1，X2，…，Xl，…}，随机变量Xl(l=1，2，…) 的发生时刻定义在状态空间T={t1，t2，…，ti-1，ti，tj…}，若马尔可夫链在Xl节点处于状态ti，移动到Xl+1节点时其状态为tj，将转移概率记作

pij=P(Xl+1=tj|Xl=ti)

(2)

马尔可夫链中Xl到Xl+1之间所有状态的转移概率集合组成的矩阵称为状态转移概率矩阵，其表达式如下

(3)

状态转移概率矩阵具有以下两个性质

pij≥0，i=1，2，…，m；j=1，2，…，n

(4)

(5)

式(1)表示下一个保障节点Xl+1发生的状态tj仅与当前保障节点Xl的状态ti相关，与之前已经发生过的保障节点X1，X2，…，Xl-1均无关，但因Xl与Xl-1相关，结合式(2)，可以通过Xl-1预测保障节点Xl的时刻，继而预测Xl+1的状态。图4所示的3条马尔可夫链，只要x1发生，即可预测每一保障节点的时刻值，在前序节点发生时，及时修正预测模型。

2 航班客舱保障过程协同预测方法

2.1 转移概率矩阵的生成

根据机场航班客舱保障过程的历史数据得到保障节点的时间分布，然后对其分段与聚类。保障节点的时间序列通常呈现不均衡分布，有些区域时间点分布紧凑，有些区域时间点分布稀疏，而基于密度的聚类方法对此类问题有较好的聚类效果。

DBSCAN是密度聚类的代表性算法，基于一组邻域 (eps，minPts) 来描述样本集的紧密程度，其中，eps描述某一样本的领域距离阈值，minPts描述某一样本的距离为eps的领域中样本个数的阈值。可以对任意形状的稠密数据集聚类，不仅简化样本数据，优化预测过程，还能发现数据集中的异常点，具有很强的抗噪性，减少数据波动对预测结果的影响。

客舱保障节点的历史数据经过聚类算法处理后，由时间点序列转化为时间簇序列，但是由于时间点分布不均匀，会得到很多尺寸不一样的簇。构建马尔可夫链来描述客舱保障节点的预测过程，其节点之间的转移概率用不同序列的簇之间的联系来描述，所以簇尺寸的选取对预测精度有很大的影响。如果簇的尺寸太小，会使得转移到该簇的状态很少，其转移概率在转移概率矩阵中不占优势，从而容易丢失该数据对预测结果的影响；如果簇的尺寸太大，导致预测的范围太大，会使预测精度降低，不具代表性。对于此问题，对聚类得到的时间簇序列做了进一步处理，通过合并、分割得到合适尺寸的簇作为马尔可夫链的状态空间。

在提取航班客舱保障节点历史时刻的分布特征后，将训练数据的时间点序列转换为簇序列，通过统计两个保障节点间训练数据从一个簇转移到另一个簇的频率作为转移概率，进而构建马尔可夫链的转移概率矩阵。Thf到Tuv的马尔可夫链转移概率计算公式为

phu=p(xu=Tuv|xh=Thf)=

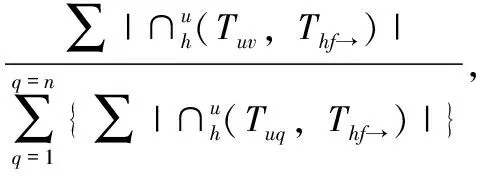
(6)

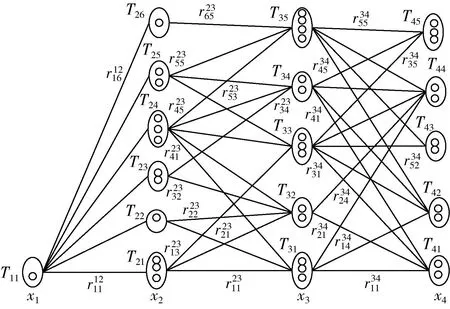
图5 簇序列转移

以保障节点x2到节点x3为例，其转移概率矩阵为

2.2 “马氏性”检验

用 (gij)i∈(1，m)，j∈(1，n)表示转移频数矩阵，“边际概率”为转移频数矩阵的各列之和与全部元素之和的比值，用P·j来表示，即

(7)

(8)

表1 马尔可夫性检验结果

2.3 DBSCAN-SMMC预测方法

根据航班客舱保障过程的马尔可夫链模型，设计了一种协同预测方法，具体步骤如下：

步骤1 初始化处理。收集机场一段时间内航班的实际运行保障数据，对数据进行转换、删除、分类、清洗等预处理。整理预处理后的数据，经过DBSCAN聚类算法处理后得到马尔可夫链的状态空间。

步骤2 初始概率的确定。首个节点的预测值可通过历史先验信息由极大似然估计法来确定，即

(9)

步骤3 转移概率矩阵构造。结合式(6)，可得节点之间的转移概率矩阵。

步骤4 “马氏性”检验。根据转移概率矩阵检验航班客舱保障节点状态序列的马尔可夫性。

步骤5 概率计算与推理。根据转移概率矩阵，以转移到下一节点的概率最大的时间簇作为初始预测结果，该时间簇的中心点即为保障节点的初始预测值。以保障节点xh转移到节点xu为例，保障节点xh的状态为Thf时，转移概率最大的时间簇Tuq的中心点作为保障节点xu的初始预测值，其表达式为

phu=p(xu=Tuq|xh=Thf)=

max{p(xu=Tu1|xh=Thf)，…，p(xu=Tun|xh=Thf)}

(10)

步骤6 预测更新。随着客舱保障节点的发生，其预测值被实际值代替，相应保障节点的状态也发生变化，根据实际值更新后续节点的预测结果，直至航班的客舱保障节点全部完成。

3 实验与分析

3.1 数据来源及预处理

仿真数据来源于国内某大型机场某季度的实际运行过程，包括进离港航班的所有字段和保障节点信息，具体数据样例如表2和表3所示。由该机场某季度实际运行的航班客舱保障数据作为样本，构成马尔可夫链的状态空间，从而开展客舱保障过程的预测。由于远机位的数据较少，作为样本不具有代表性，因此只针对近机位过站航班的客舱保障过程分析。

表2 航班信息数据样例

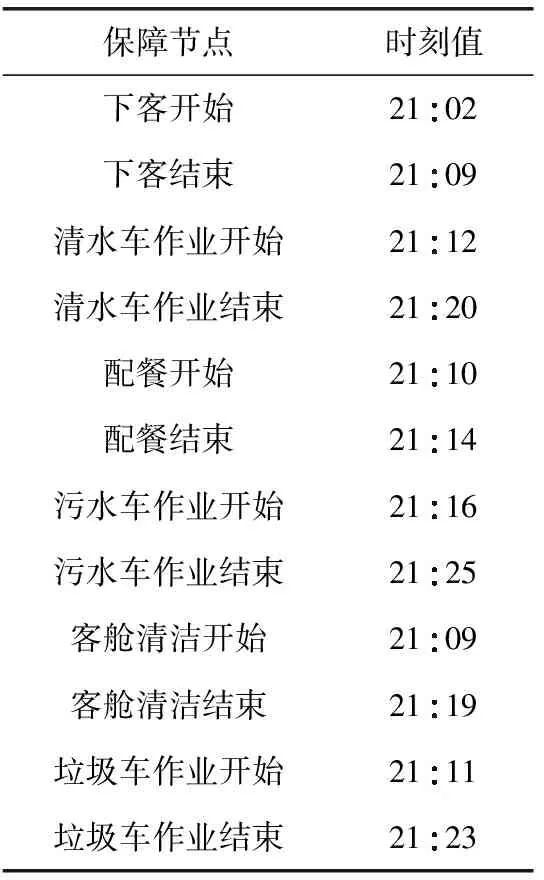
表3 客舱保障过程节点时刻数据样例

由于机型的不同会导致载客量存在差异，从而影响航班客舱保障过程的时间，因此在概率推理时按照客座数将航班机型分为3类，如表4所示。同时，航线性质不同，所需保障资源也有所不同，从而影响保障时间，根据航线性质划分为国内近程、国内远程和国际航线3类。考虑以上影响因素，分别构建马尔可夫链转移概率矩阵。

表4 航班机型分类

3.2 仿真验证

根据历史数据对构建的马尔可夫链的3个初始保障节点开展极大似然估计，得到初始保障节点的先验概率模型，即下客结束、配餐开始、客舱清洁开始3个节点发生时间的先验概率模型，如图6所示。

图6 初始保障节点先验概率模型

历史数据按照机型、航线性质分类后应用DBSCAN聚类算法，设其领域距离阈值eps=1，样本个数阈值为minPts=30，分别得到各自的马尔可夫链的状态空间，把此数据作为训练集，得到节点之间各状态的转移概率矩阵，基于得到的转移概率矩阵开展马尔可夫链中各保障节点的概率推理，以转移到下一节点的概率最大的状态作为初始预测结果，以该状态的中心点作为预测值。选取该机场某日山东航空股份有限公司出港航班号为4752的航班实际的客舱保障流程数据仿真验证，结果如图7所示。

图7 航班到达后的初始预测结果

随机选取该机场下一季度30个过站航班的客舱保障过程数据，对每一个保障节点做单独预测，各节点的预测时间均以马尔可夫链模型中上一节点为基准，各航班客舱保障过程的5个关键节点预测结果如图8所示。

图8 多航班关键节点预测结果

3.3 结果分析

为了验证本文提出的DBSCAN-SMMC预测方法的精密度和准确性，对上述30个航班的客舱保障过程预测结果分析，结合机场实际运行所允许的1 min保障时间置信区间，计算各关键保障节点的均方根误差(RMSE)和平均绝对误差(MAE)，即

(11)

(12)

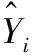
上述多航班预测计算结果如表5所列。

表5 多航班预测分析结果

可知，所有节点均方根误差RMSE的均值为1.1331，表明结果能够满足保障过程的预测要求，且有6个节点的RMSE小于1，能够很好地反映出预测结果的精密度。平均绝对误差MAE的均值为0.6061，且所有MAE稳定控制在2 min以内，符合机场运行相关标准的要求，有9个节点的MAE在1 min之内，表明预测结果有较高的准确性。同时，本算法的时间复杂度和响应时间可以满足预测过程的时效性。

3.4 对比分析

为了进一步验证马尔可夫预测模型的可行性，选择与BP神经网络预测模型作对比。因清水车作业与其它客舱保障过程不冲突，开始时间相对自由，但作业结束时间会影响航班后续计划；另外，客舱清洁过程与垃圾车作业过程相互制约，客舱清洁结束后垃圾车作业才能结束，为后续航班保障释放资源，所以选取这两个关键保障节点，直观比较两种方法的预测结果，如图9所示。

同时，计算两种方法的平均绝对百分误差(MAPE)来衡量模型预测结果的好坏，MAPE越小表示预测模型越好，当MAPE大于100%时为劣质模型；计算R-平方(R2)来比较两个模型的拟合优度，R2越接近1，表明回归拟合程度越好

(13)

(14)

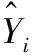
计算结果见表6。可知，两个关键节点的DBSCAN-SMMC预测方法均比BP神经网络的MAPE低，而且均在15%以下，表明该模型优于BP神经网络模型，且模型效果较好；DBSCAN-SMMC预测方法的R2值均在0.8以上，远大于BP神经网络模型的R2值，拟合效果更好。

表6 预测参数对比

综上可知，本文提出的DBSCAN-SMMC方法能够满足过站航班客舱保障过程预测的基本要求。

4 结束语

针对客舱保障过程多条件约束、多资源协同的问题，构建了其实际运行过程的马尔可夫模型；针对保障节点数据分布不均衡的问题，改进了DBSCAN对时间序列聚合，提高了聚类的精准度，得到了客舱保障过程的DBSCAN-SMMC预测方法。研究表明，航班机型、航线性质是航班客舱保障过程考虑的首要条件，是确定马尔可夫模型转移概率矩阵的关键因素；客舱保障节点的时间预测依赖于上一节点的状态。航班客舱保障过程受多种因素影响，本文只考虑了机位、航班机型、航线性质等首要影响因素，因此尚存在一定不足，下一步将综合考虑航班执行时段、旅客等因素，细化模型训练数据；另外可以进一步研究其它状态划分方法对马尔可夫预测模型精度的影响。