多策略改进的被囊群算法在入侵检测中的应用

汪 杰，汪祖民

(大连大学 信息工程学院，辽宁 大连 116622)

0 引 言

近年来，智能群优化算法被广泛应用于机器学习用来解决各种场景的入侵检测[1]。为提高入侵检测性能，文献[2]将改进灰狼优化算法应用于BP神经网络。文献[3]提出一种基于随机森林和人工免疫的入侵检测算法，并构建了抗体森林的模型。文献[4]在鲸鱼算法中引入自适应步长和拥挤度因子以及高斯变异算子，并将改进后的优化算法对支持向量机算法的参数进行寻优。文献[5]将人工蜂群算法用于特征提取，并利用XGBoost算法对需要评价的特征进行分类。文献[6]提出一种并行技术改进支持向量机算法在大规模数据下训练速度慢的问题，并融合改进后的布谷鸟搜索算法设计了工控入侵测模型。

综上所述，机器学习算法在入侵检测的研究中十分常见。但是部分机器学习算法本身的性能不足，如文献[7]实验证明同其它机器学习算法比较，XGBoost在各种入侵检测中表现更为优异。同时由于大部分寻优算法收敛速度慢，易陷入局部最优解，因此本文提出利用改进被囊群算法对XGBoost算法的参数和数据集特征数量进行寻优，提高入侵检测性能。仿真结果表明，相比于其它机器学习算法，该入侵检测模型的性能更好。

1 被囊群优化算法

被囊群优化算法(tunicate swarm algorithm，TSA)[8]是由Kaur等提出的一种元启发式算法，其性能在74个基准问题中得到了有效证明。其数学模型如下。

1.1 喷气推进行为

1.1.1 避免搜索个体间冲突

为了避免搜索个体间的冲突，使用向量A来计算新的个体位置

(1)

式中：G表示重力

G=C1+C2-2·C3

(2)

M表示各个体间的社会力量

(3)

C1，C2，C3都是属于[0，1]的随机数，Pmax和Pmin分别是社会力量的初始速度和从属速度，上述公式有助于个体在给定的搜素空间中随意移动，并避免不同搜索个体之间的冲突。

1.1.2 向最佳搜索个体移动

个体在避免群体间冲突后向当前最佳搜索个体的位置移动，由以下公式计算个体与最佳搜索个体间的距离

PD=Pbest-r·P(x)

(4)

式中：P(x) 表示第x次迭代时被囊群个体的位置，r是属于[0，1]的随机数，Pbest为当前最佳搜索个体的位置。

1.1.3 向最佳搜索代理汇聚

当每个个体求得自身在当前迭代与最佳个体间的距离后，个体开始向当前迭代中的最佳个体位置汇聚

(5)

1.2 群体行为

TSA通过整合当前个体的位置和上一次迭代个体的位置，来模拟被囊群的群体行为，其数学公式定义如下

(6)

2 多策略改进被囊群优化算法

2.1 Tent混沌映射

基本被囊群算法的初始位置是随机生成的，所以种群的初始位置在空间中分布不均匀，会降低种群的多样性并影响收敛速度。因此本文提出采用混沌映射[9]来初始化种群，相比于另一种常用的logistic混沌映射，Tent混沌映射具有更好的遍历性，能够在[0，1]之间产生分布较均匀的初始值。因此基于Tent映射的TSA具有更好的种群多样性和收敛速度。

Tent映射的表达式如下

(7)

式中：i=1，2，3…，P为种群规模，n=1，2，3…，D表示当前求解问题的维度。

通过式(7)可以得到P×D个混沌序列，再将其代入式(8)初始化种群位置

(8)

式中：ub代表个体位置的最大边界值，lb代表个体位置的最小边界值。

2.2 自适应步长

在标准被囊群算法中，算法的探索和开发能力主要受到群体行为的影响，而式(6)中的参数C1影响着群体行为的步长。当C1越小时，步长越大，有利于算法的全局探索能力；当C1越大时，步长越小，有利于算法的局部探索能力。而算法在迭代前期，需要更强的全局探索能力，帮助算法跳出局部最优解；而在迭代后期，则需要更强的局部探索能力，帮助算法获得更高的求解精度，综上所述，C1的值应该随着迭代次数的增加而逐渐增大。由于标准算法中的C1是[0，1]之间的随机数，所以在群体位置更新时，容易产生盲目性，使算法难以获得更快的收敛和更高的精度。

针对以上问题，本文将C1由如下公式代替

(9)

式中：t是当前迭代次数，Tmax代表最大迭代次数，ω是一个惯性权重，它随着迭代次数的增加而自适应地减小。将式(9)代入式(6)更新为

(10)

2.3 莱维飞行

被囊群中个体的移动主要是依靠最优个体的位置信息进行移动，其中式(1)中的向量A决定了个体的更新距离，其值更是由多个范围为[0，1]的随机数决定，这大大降低了个体移动的多样性。当最优个体陷入局部最优解时，被囊群中的其它个体在向最优个体移动时，很难再搜索到全局最优解，因此本文提出利用莱维飞行[10]来增强个体向当前最优位置移动时的路径扰动，以此帮助算法更好的跳出局部最优解，改进公式如下

(11)

(12)

PLevy(x)=P(x)+ω·s·(Pbest-P(x))

(13)

上述改进后的被囊群优化算法(improved tunicate swarm algorithm，ITSA)的算法流程如下：

步骤1 种群个体的初始化位置由Tent混沌映射决定。

步骤2 初始化算法的各个参数。

步骤3 计算所有个体的适应度值，此时最优解的值就是当前最优个体的值。

步骤4 根据式(1)到式(5)进行个体位置更新。

步骤5 根据式(13)利用莱维飞行策略对每个个体施加扰动，其中个体移动步长由自适应步长式(9)得出。

步骤6 根据式(10)进行群体位置更新，其中个体移动步长由自适应步长式(9)得出。

步骤7 检测每个个体的位置是否超出边界，并调整超出边界的个体位置。

步骤8 计算个体经过群体行为后的适应度值和经过莱维飞行扰动后的适应度值，将两者中的最佳适应度值作为当前最优解。

步骤9 算法满足停止条件则停止，否则重复步骤4～步骤8。

步骤10 返回最优解。

3 ITSA-XGBoost入侵检测模型的构建

XGBoost是机器学习中梯度提升树的高效实现，XGBoost中有许多的参数难以整定，同时不同数量的特征选择对检测精度有较大的影响，本文主要利用ITSA算法对选取的部分XGBoost参数和特征数量进行寻优。寻优的参数及范围见表1。

表1 参数选取

表2中max_feature代表数据集可选取的最大特征数量。

表2 12个测试函数

利用ITSA对XGBoost参数和特征数量寻优的具体流程如下：

步骤1 删去入侵检测训练集和测试集中的重复数据，对离散数据特征进行映射，将离散特征转化为数字型特征，对数据集进行归一化处理。

步骤2 通过递归式特征消除(recursive feature elimination，RFE)[12]对特征进行排序，将XGBoost作为迭代分类器，得到排序后的特征。

步骤3 利用ITSA算法对XGBoost参数和特征数量进行寻优，将在训练集中训练好的XGBoost模型用来对测试集进行预测，并把测试集的准确度作为适应度值返回，在达到最大迭代次数前，找到使测试集准确度最高的参数及特征数量。

步骤4 输出对XGBoost模型寻得最优解后的测试集分类结果。

ITSA-XGBoost入侵检测模型流程如图1所示。

图1 ITSA-XGBoost入侵检测模型

4 实验设置

4.1 实验环境

实验硬件采用Intel(R) Core(TM) i5-10400H CPU+GeForece GTX 1660Ti+16 GB内存；软件环境，在ITSA性能测试中采用MATLAB R2022a，在ITSA-XGBoost入侵检测实验中采用Python 3.9.5。

4.2 ITSA性能测试

在本文中，被囊群算法的参数设置见表1，其中种群数量pop为50，最大迭代次数Max_iter为500，同时为了验证ITSA的算法性能，本文将灰狼优化算法(grey wolf optimizer，GWO)[13]、海鸥优化算法(seagull optimization algorithm，SOA)[14]、TSA和ITSA作对比。本文采用12个测试函数检验ITSA的寻优能力，其中F1～F4为多维单峰函数，F5～F8为多维多峰函数，F9～F12为固定维度函数。上述12个测试函数表达式见表2。收敛曲线如图2所示。

图2 各算法在12个函数上的收敛曲线对比

如图2所示，在寻找最优解方面，ITSA在多维单峰函数上提升较大，而在多维多峰函数和固定维度函数上相较于TSA也有不小的提升。在收敛速度方面，ITSA在不同函数上的表现都很好。因此实验验证利用Tent混沌映射、自适应步长和莱维飞行能够使算法提高收敛速度，同时在算法迭代后期拥有跳出局部最优解的能力。

4.3 ITSA-XGBoost模型性能分析

4.3.1 入侵检测数据集

本文采用由澳大利亚网络安全中心在2015年创建的UNSW-NB15[15]数据集对模型进行性能测试。该数据集中共有257 673条样本，其中175 341条训练集样本，82 332条测试集样本。但是其中有相当多的重复样本，在将无用的“id”列剔除后，删除重复样本，此时数据集的样本数量与分布见表3。

表3 UNSW-NB15的训练集和测试集

如表3所示，除Normal类为正常网络行为，剩余9类均为攻击行为。

4.3.2 实验基本设置

为测试ITSA-XGBoost模型的性能，将ITSA算法与TSA算法中的种群数量设为50，迭代次数设为100。对于UNSW-NB15数据集，在将“label”和“attack_cat”列抽离后，对离散数据特征进行映射，将离散特征进行Label-Encoder编码转化为数字型特征后，对数据集所有列进行归一化处理，最后利用RFE对特征进行排序，得到排序后的42个特征值供ITSA-XGBoost模型进行特征寻优。

4.3.3 评估指标

模型评价标准定义请参考文献[16]，定义如下：

准确率(Accuracy，Acc)

(14)

精确率(Precision，Pre)

(15)

召回率(Recall)

(16)

F1-Score

(17)

AUC(area under curve)是ROC(receiver operating characteristic)曲线下的面积，定义如下

(18)

上述公式中，TP(true positive)是正确分类到正常网络行为的样本数，TN(true negative)是正确分类到攻击行为的样本数，FP(false positive)是将攻击行为错误分类为正常网络行为的样本数，FN(false negative)是将正常网络行为错误分类为攻击行为的样本数。

4.3.4 ITSA优化XGBoost效果分析

为测试ITSA-XGBoost模型在参数寻优上的优越性，将其与TSA-XGBoost模型进行比较。设置TSA和ITSA算法的种群数量为50，最大迭代次数为100。两种模型在UNSW-NB15数据集上的准确率和ROC曲线如图3所示。

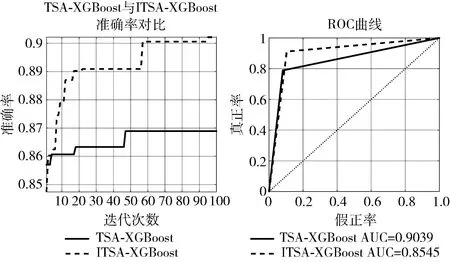
图3 TSA和ITSA结合XGBoost算法性能对比

如图3所示，在准确率对比曲线中，ITSA-XGBoost模型在收敛速度和准确率上均优于TSA-XGBoost模型，且ITSA-XGBoost模型不易陷入早熟收敛，在迭代后期依旧有跳出局部最优解的能力。在ROC曲线中，ITSA-XGBoost模型的AUC值为0.9039，而TSA-XGBoost模型的AUC值为0.8545，这表明ITSA-XGBoost模型获得了更高的真正率和更低的假正率。综上，ITSA-XGBoost模型在参数寻优上优于TSA-XGBoost模型。

4.3.5 ITSA-XGBoost模型二分类和多分类性能对比

为体现ITSA-XGBoost模型的性能，本文选取了文献[17]中的人工神经网络算法(artificial neural network，ANN)、逻辑回归算法(logistic regression，LR)、K近邻(k-nearestneighbor，KNN)、支持向量机算法(support vector machine，SVM)、决策树算法(decision tree，DT)进行性能对比，对比结果见表4、表5。

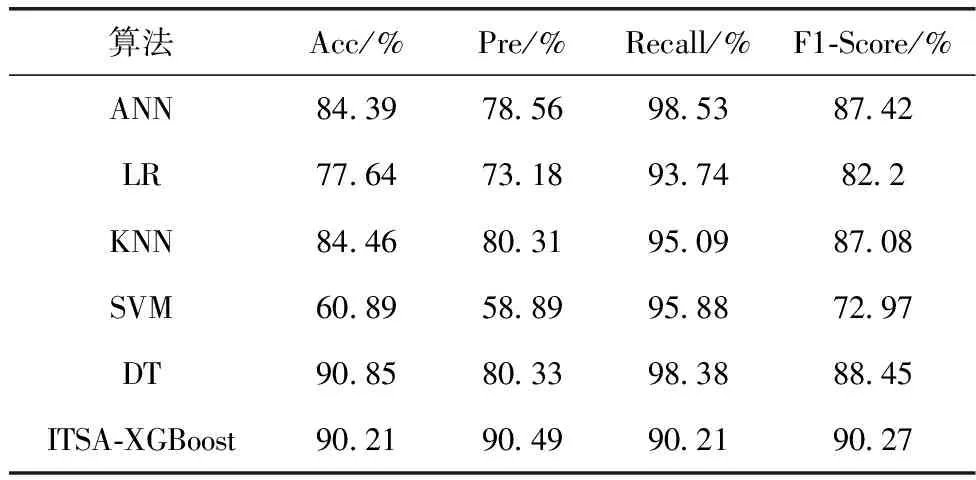
表4 二分类性能对比

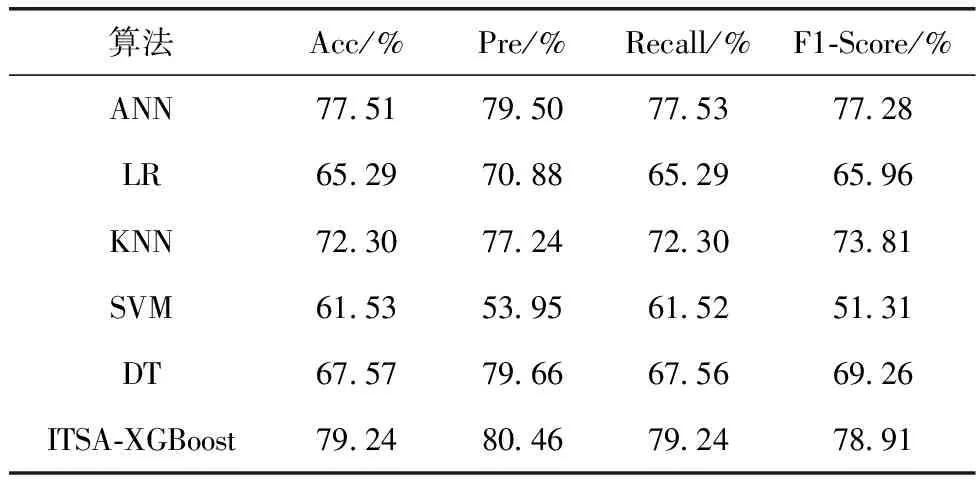
表5 多分类性能对比

通过表4的实验结果可以看出，在二分类性能对比中，ITSA-XGBoost模型在准确率上除了比决策树算法(DT)低0.64%，均高于其它算法，在精确率和F1-Score上均优于其它算法，而在召回率上则低于其它算法。

通过表5的实验结果可以看出，在多分类性能对比中，ITSA-XGBoost模型在准确率、精确率、召回率和F1-Score上均优于其它算法。

最后，为体现ITSA-XGBoost模型的优越性，本文选取了另外6篇论文中的随机森林树算法(random forest，RF)[18，19]、RepTree算法[20]、IELM算法[21]、深度置信网络算法(deep belief network，DBN)[22]、CNN-BiLSTM算法[23]进行二分类和多分类的准确率对比。对比结果见表6。

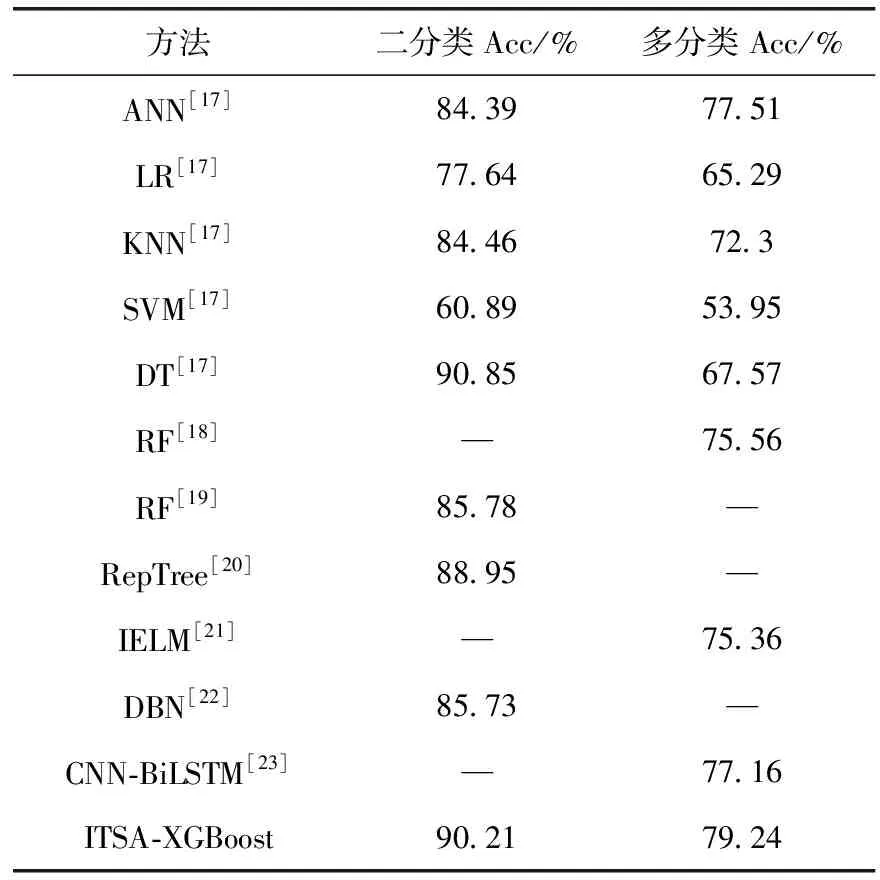
表6 测试集准确率对比

ITSA-XGBoost模型在二分类中准确率除了比决策树算法(DT)低0.64%，均高于其它算法。而在多分类中则均优于其它所有算法。因此，与其它算法相比，ITSA-XGBoost更加适合入侵检测。

5 结束语

本文利用Tent混沌映射，自适应步长和莱维飞行3种策略改进被囊群优化算法，并用于XGBoost参数寻优和特征选择以构建入侵检测模型。实验结果表明，改进后的ITSA相比于其它优化算法收敛速度更快，且具有跳出局部最优解的能力。同时相较于其它机器学习算法，在UNSW-NB15数据集中，ITSA-XGBoost模型的检测性能更好。在未来的研究中，将通过生成对抗网络等方法处理少数样本数据，提高入侵检测的性能。