基于深度估计置信度的聚焦形貌恢复

史艳琼，查昭，张文亮，戴尔愉，陈中

（安徽建筑大学机械与电气工程学院，安徽 合肥 230601）

0 引言

聚焦形貌恢复（SFF）［1］技术是一种利用二维图像信息恢复物体三维形貌的方法，其对采集到的离焦序列图像使用聚焦评价函数获得象征聚焦程度的聚焦评价值，通过搜索使窗口聚焦评价函数值最大的图像位置来估计景物的深度信息，以此实现三维形貌恢复。SFF 技术原理简单、设备成本低、体积小，且具有较高的重建精度，因此，在显微三维成像［2］、光学三维测量［3］等领域有着广泛的应用。

在离焦序列图像的采集过程中，由于环境的影响和相机本身的限制，采集到的图像会不可避免地带有噪声信息，这使得聚焦评价结果不准确，最终导致重建精度降低。现有研究主要从高性能聚焦评价函数设计［4-6］和深度图优化［7-9］两方面入手提高SFF 精度。在高性能聚焦评价函数设计方面：文献［10］提出一种自适应窗口大小选择算法和自适应加权改进拉普拉斯算子；文献［11］提出名为环形差分滤波器的新型聚焦评价函数；文献［12］提出基于颜色空间的聚焦评价方法，根据彩色图像中心像素与邻域像素色彩的差异测量聚焦程度。在深度图优化方面：文献［13］提出一种可靠性测量方法，用于评估SFF 技术中获取的深度图质量，探测并移除深度图中低准确度区域，减少噪声对重建质量的干扰；文献［14］提出对聚焦评价序列正则化处理，并使用图像序列作为结构先验约束正则化的方法；文献［15］基于图像灰度曲线与聚焦评价值之间的相关性对深度信息进行引导滤波，提高深度图质量。然而，上述方法仍存在一些不足：文献［13］提出的方法虽然可以识别出大部分深度信息不可靠的像素并进行移除，但并未对移除所产生的空洞进行填补，导致重建结果不完整；文献［14］提出的方法虽然对于数据中的离群值有鲁棒性，但需要使用彩色图像作为结构先验，这一缺点使其应用范围狭窄；文献［15］提出的方法虽然可以有效减轻噪声对重建结果的影响，获得完整且连续的物体三维形貌，但由于未考虑噪声对图像灰度曲线的影响，优化过程会对物体原本结构特征产生影响，使得重建结果不够精确。

针对以上方法的不足，为尽可能抑制噪声的影响并使得重建后的三维形貌完整且精确，本文从深度图优化方面入手，在基于相关性的引导滤波基础上提出基于曲线相似度的概念，使其更具泛用性；同时添加修正项，改善灰度曲线受噪声影响振荡导致置信度错误降低的情况；在此基础上，通过计算聚焦评价曲线与灰度曲线间的相似度，判断像素聚焦评价结果是否受到噪声影响导致深度估计出错，得到整幅图像深度估计的置信图，并将置信图作为引导图；最后使用引导滤波对深度图进行处理，优化初始深度图，使最终的重建结果精确且连续。

1 聚焦形貌恢复技术

1.1 基本原理

聚焦形貌恢复技术利用了相机光学成像原理进行三维重建［16］，如图1所示。按照一定的步长λ移动物体或相机改变两者间的距离对同一平面进行拍摄，采集到包含该平面内物体所有点从模糊到清晰再到模糊的序列图像后，使用聚焦评价函数对每幅图像进行处理，获得所有像素在当前位置的聚焦值，聚焦值随聚焦程度变化，在最佳聚焦位置达到最大值。使用最值搜索方法获得所有像素的最佳聚焦位置，并结合已知的步长信息即可估计出图像中像素的深度值。

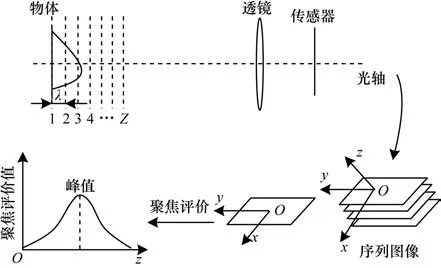
图1 聚焦形貌恢复原理Fig.1 Principle of shape from focus

1.2 聚焦评价函数

目前已经有多种聚焦评价算子，PERTUZ等［17］整理了36 种聚焦评价算子并按照原理的不同分为6 类，在噪声强度、对比度、饱和度、窗口大小等不同条件下对这些算子的性能进行实验评估。常见的聚焦评价函数主要有空域、频域、统计学3 种类别。空域聚焦评价算子在空间域内根据图像灰度变化的剧烈程度评估图像聚焦程度：图像越清晰，图像灰度值变化越剧烈；图像越模糊，图像灰度值变化越平缓。通常使用图像梯度算子来检测图像灰度的变化情况，使用较为广泛的算子有改进的拉普拉斯算子［1］、Tenengrad 算子［18］、Roberts 算子等。空域聚焦评价算子具有计算简单快速、对灰度变化灵敏等优点，但在低纹理图像中，由于图像灰度变化不明显，这类算子性能较差，并且因为高灵敏度的特点，在实际应用中很容易受到噪声的影响。常见的基于频域的聚焦评价函数有基于傅里叶变换、基于小波系数和［19］、基于离散余弦变换［20］等方法，这类方法将图像转换到频域计算，根据图像频率能反映图像灰度变化这一特性，通过图像高频系数分布判断图像的聚焦程度。频域聚焦评价算子鲁棒性更强，但由于需要将图像转换到频域，这类方法通常需要较大的计算量，花费时间长，不适合实时计算。基于统计学的聚焦评价方法主要根据像素邻域内如灰度方差、灰度直方图、熵等统计数据计算聚焦程度，常用方法有灰度方差函数［21］、熵函数［22］等，这类方法以一定区域范围内的统计数据作为评价依据，灵敏度较低。

基于上述传统算子结合峰值搜索方法可以得到初始的深度图，但此时深度图中有大量错误的深度值，三维形貌恢复的精度和准确度都无法达到要求，还需要对其进行优化，提升重建精度。

2 基于深度估计置信度的聚焦形貌恢复

2.1 曲线相似度的深度估计置信度计算方法

根据光学成像原理可知，相机沿z轴移动扫描成像时，离焦序列图像上同一位置的像素会经历从模糊到清晰再到模糊的过程。像素p的灰度曲线由各序列图像上相同位置像素的灰度值构成，表示为：

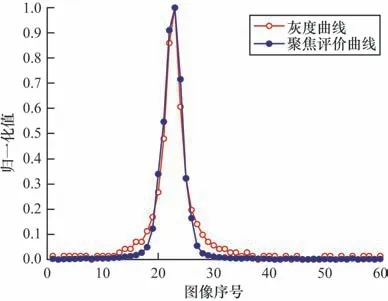
图2 像素点的灰度曲线与聚焦评价曲线Fig.2 Grayscale curve and focus measure curve of pixel

像素深度估计的置信度可用2 条曲线间的相似度进行度量，相似度计算方法主要有基于皮森相关系数、基于欧氏距离、基于余弦相似度等。

皮尔森相关系数表示为：

余弦相似度表示为：

通过计算2 个向量的夹角余弦值来评估它们的相似度，余弦值越小则2 个向量越相似。

分别选取图像上深度估计准确的p1点和深度估计错误的p2点，图3 中展示了这2 个像素点相应的聚焦评价曲线与灰度曲线，其中，p1点坐标为（939，593），p2点坐标为（288，765）。p1点深度估计准确，灰度曲线与聚焦评价曲线在图像1～图像6 中呈上升趋势，从图像6 开始大体上呈下降趋势，根据计算结果，p1点的皮尔森相关系数ρp1=0.857 5；p2点深度估计错误，当灰度曲线在图像17～图像24 中呈下降趋势时，聚焦评价曲线却呈上升趋势，该点皮尔森相关系数ρp2=0.061 3。计算结果与上述推论保持一致，2 条曲线间的相似度在一定程度上可以反映初始深度估计的可靠性。

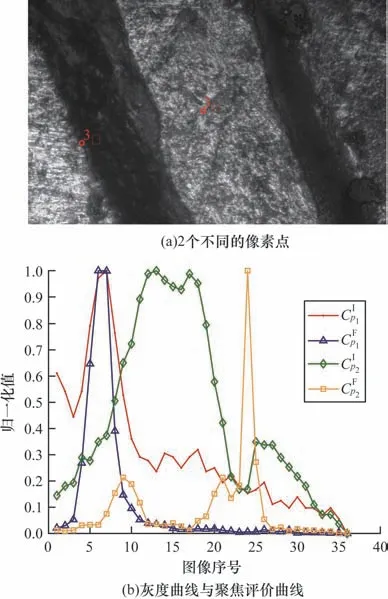
图3 不同像素点的灰度曲线与聚焦评价曲线Fig.3 Grayscale curves and focus measure curves of different pixels

除此之外，笔者在实验过程中发现，噪声对像素点的影响较大时会导致灰度曲线产生剧烈的振荡，在这种情况下，即使聚焦评价曲线具有良好的单峰性且深度估计正确，也会因为灰度曲线的异常导致2 条曲线的相似度减小，从而使该点置信度降低，如图4 所示。

图4 灰度曲线受噪声影响异常振荡的情况Fig.4 Abnormal oscillation when grayscale curve affected by noise

针对由灰度曲线振荡引起的像素估计深度置信度降低的情况，分析正常灰度曲线与异常灰度曲线可知，当灰度曲线大幅振荡时，其均方根值会比正常情况下呈现单峰趋势的均方根值大，而聚焦评价曲线保持单峰趋势，其均方根值几乎不变。因此，在原有相似度计算公式上再加上聚焦评价曲线与灰度曲线的均方根值之差作为修正项，改善上述情况：

将修正项与相似性度量相加得到最终的置信度计算公式，基于皮尔森相关系数和基于余弦相似度的置信度计算公式分别表示为式（6）和式（7）：

使用上述置信度计算公式对图像中每一个像素进行估计，即可获得该离焦序列图像深度估计的置信图。

2.2 引导滤波

为了获得更为准确与连续的深度图，将置信图作为引导图，通过引导滤波对初始深度图进行优化。作为引导图的置信图含有一些深度图中不存在的额外的结构信息，引导滤波可以将这些结构信息传输到初始深度图中，帮助改善初始深度图中的深度信息［23］。引导滤波［24］是一种根据局部线性模型原理，参考引导图像内容对输入图像进行滤波输出的算法。它能在充分使用引导图像变化细节的同时，保留输入图像整体特征，使输入图像与输出图像的结构相似度更大。

在引导滤波算法中，记引导图像为G，输入图像为P，输出图像为Q，则引导图像I与输出图像Q在以k为中心的二维滤波窗口ωk内有如下线性关系：

其中：i为窗口ωk中像素位置索引值；ak、bk为窗口中的2 个线性系数。求得ak与bk即可获得滤波结果，可转化为求这2 个系数最优解的问题，表示为：

其中：Pi为滤波输入；λ为归一化因子。使用线性回归求得公式的解为：

其中：μk与分别表示引导图G在窗口ωk中的均值与方差表示输入图像P在窗口ωk中的均值为窗口ωk中的像素数。

2.3 聚焦形貌恢复算法步骤

根据上述原理设计相应的聚焦形貌恢复算法，具体步骤如下：

1）使用聚焦评价函数计算序列图像I中各个像素点的聚焦评价值：

2）使用基于高斯函数的最小二乘拟合法对离散的聚焦评价值进行拟合，获得最大值位置，将其作为像素点的初始深度值D(p)：

3）根据像素灰度值与聚焦评价值在不同聚焦程度下的变化规律，使用相似性度量方法计算各个像素点深度估计的置信度，集合所有像素的置信度得到初始深度估计的置信图。

4）将置信图作为引导图对初始深度图进行引导滤波，使得深度图更加精确且连续，最终获得景物的三维信息。

3 实验与分析

为了验证形貌恢复的精度及有效性，对仿真离焦序列图像与真实采集离焦序列图像进行实验，并将所提方法的结果与传统方法、可靠性度量方法［13］（R-measure）、基于相关性的引导滤波方法［15］（Xcor）进行对比以直观地验证改进效果。由于可靠性度量方法会造成深度信息的缺失，因此不对其进行定量的评价指标对比。同时，为了验证所提方法的抗噪性能，对仿真离焦序列图像加入方差为0.005 的高斯噪声，得到加噪的仿真离焦序列图像进行抗噪性验证。为了控制变量，所有实验中的聚焦评价算子均使用Tenengrad 算子，最值搜索方法均使用高斯拟合峰值搜索法，仿真数据实验窗口大小为5×5 像素，真实数据实验窗口大小为15×15 像素。

本文实验环境为Microsoft Windows 10、Intel Core i7-8550U CPU；运行内存为8 GB；使用软件为MATLAB R2018b。

3.1 性能评价指标

在获得重建结果后，为了定量地评估形貌恢复结果优劣，选用均方根误差（RMSE）和相关系数（Corr）进行评估。均方误差表示为：

其中：M、N分别为图像水平方向和竖直方向的像素个数；f(i,j)是深度估计值；g(i,j)是离焦序列图像真实深度值。相关系数表示为：

其中：Fij和分别为深度估计值和深度估计均值；Gij和分别为真实深度值和真实深度均值；相关系数取值范围在0 到1 之间。

3.2 仿真数据实验

实验将在3 组仿真离焦序列图像中进行，包括圆锥、正弦和余弦3 种模型。选用2 种主流离焦图像合成方法生成实验所用数据集，3 种模型的部分仿真离焦序列图像如图5 所示，其中，图5（a）是使用文献［14］提出的图像仿真离焦方法对圆锥模型与纹理图像进行处理生成的仿真离焦序列图像，图5（b）和图5（c）是使用文献［25］提出的图像仿真离焦方法合成的仿真离焦序列图像。序列图像参数如表1所示。

表1 仿真离焦序列图像参数Table 1 Parameters of simulated defocused sequence images

图5 部分仿真离焦序列图像Fig.5 Partial simulated defocused sequence images

对上述序列图像进行实验，结果如图6 所示，其中，图6（a）为初始重建结果，图6（b）～图6（e）为使用基于深度图优化的方法的重建结果，图6（f）为真实值。可以看出，经过本文方法优化后的重建结果深度变化更为连续，第2 行展示的正弦的初始重建结果有着轻微的失真，产生了锯齿状的边缘，而本文提出的优化方法改善了这一现象。定量的重建结果评价指标如表2 所示，其中最优结果用加粗字体表示。可以看出，所有的仿真离焦序列图像重建结果经优化后Corr 都有提升，且圆锥、正弦和余弦模型的重建结果评价指标中RMSE 都有减少，这说明本文提出的方法能够有效地提高聚焦形貌恢复精度。在圆锥模型的重建结果评价指标中，基于余弦相似度的优化方法RMSE 值最小，在余弦模型的重建结果评价指标中，使用基于余弦相似度的优化方法得到了比使用基于皮尔森相关系数的优化方法更低的RMSE 值和更高的Corr 值，因此，基于余弦相似度的优化方法在具有复杂深度信息的重建中有着更优的性能。

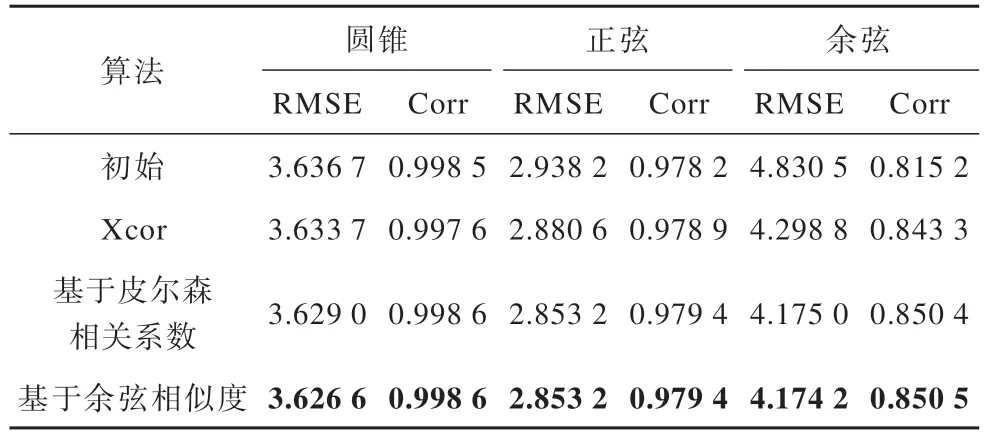
表2 仿真离焦序列图像重建结果评价指标Table 2 Evaluation indexes of reconstruction results of simulated defocused sequence images

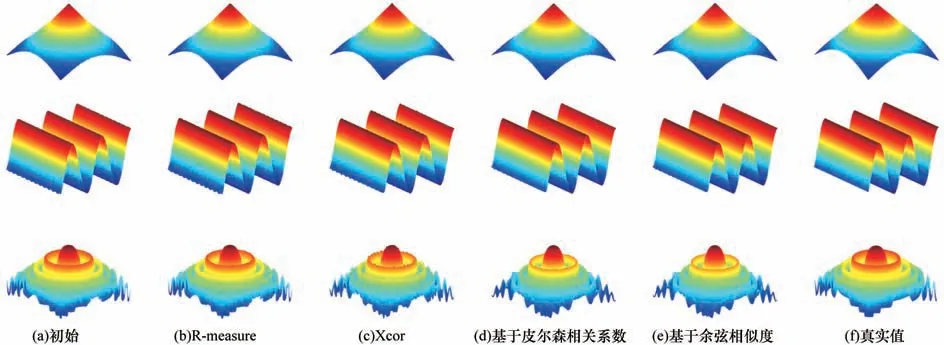
图6 仿真离焦序列图像重建结果Fig.6 Reconstruction results of simulated defocused sequence images

为了验证所提算法的抗噪性能，对仿真聚焦序列图像均添加方差为0.005 的高斯噪声并进行实验，重建结果如图7 所示。可以看出，加噪仿真离焦序列图像的初始重建结果存在大量错误估计的深度信息，且由于噪声的干扰，深度变得更加不连续。图7（b）～图7（e）展示了经优化后的重建结果，可以看出，本文所提方法相比于初始重建结果和其他优化方法有着更为光滑的表面，错误估计的深度信息也被修正过来，深度也变得更为连续，所提方法的抗噪性能得到了验证。定量的性能指标如表3 所示，其中最优结果用加粗字体表示。可以看出，经优化后的重建效果有了较明显的提升，RMSE 均有明显下降，Corr 有明显提升，这表示恢复结果与真实值之间的误差在减小的同时，与真实值的相似度也有了提升。在加噪圆锥模型和加噪正弦模型中，基于余弦相似性的优化方法以略微的差距取得了更好的恢复结果，而在加噪余弦模型中，基于皮尔森相关系数的优化方法则表现略好。

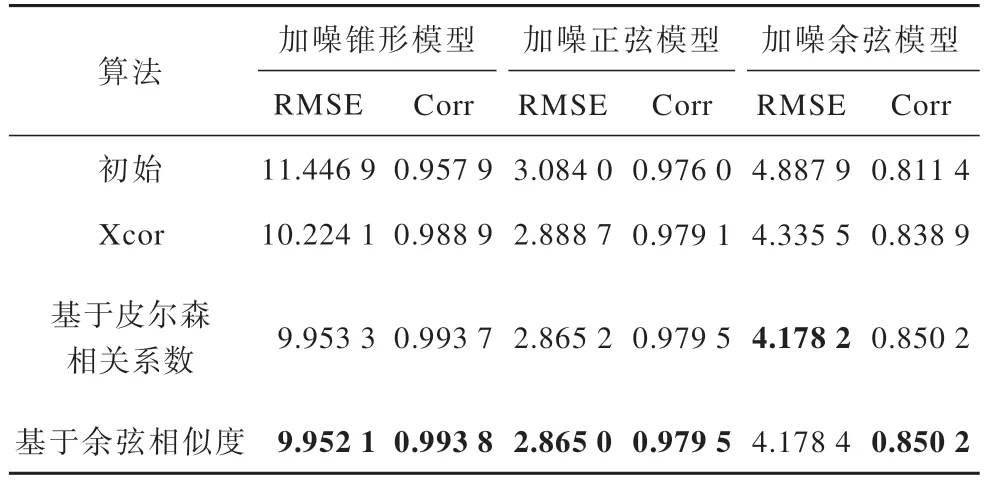
表3 加噪仿真离焦序列重建结果性能指标Table 3 Evaluation indexes of reconstruction results of noisy simulated defocused sequence images

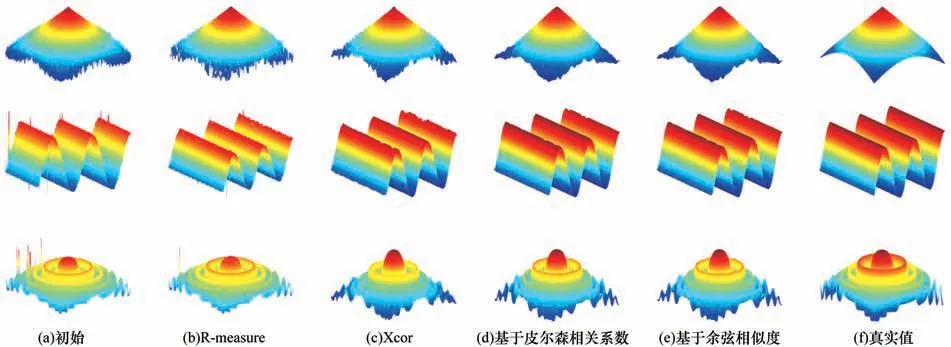
图7 加噪仿真离焦序列图像重建结果Fig.7 Reconstruction results of noisy simulated defocused sequence images

3.3 真实数据实验

为了评估所提方法在真实场景中的表现，选用CMOS 相机、PK545 步进电机、位移平台、同轴光源与环形光源搭建离焦序列图像采集系统，如图8所示。

图8 离焦序列图像采集系统Fig.8 Defocused sequence images acquisition system

实验通过步进电机带动成像系统沿Z轴移动拍摄1 mm 厚度的标准件表面获得2 组扫描离焦序列图像。采集的部分离焦图像如图9 所示，其中，第1 列为放在倾角为7°的载物台上的标准件的表面显微离焦图像，第2 列为标准件与载物台形成高度为1 mm 的台阶的显微离焦图像。真实离焦序列图像参数如表4 所示。

表4 真实离焦序列图像参数Table 4 Parameters of real defocused sequence images

图9 部分真实离焦序列图像Fig.9 Partial real defocused sequence images

通过实验对比初始重建结果、可靠性度量方法、基于相关性的引导滤波方法、使用皮尔森相关系数置信图的重建结果和使用余弦相似度置信图的重建结果，各离焦序列图像的三维形貌重建结果如图10、图11 所示。

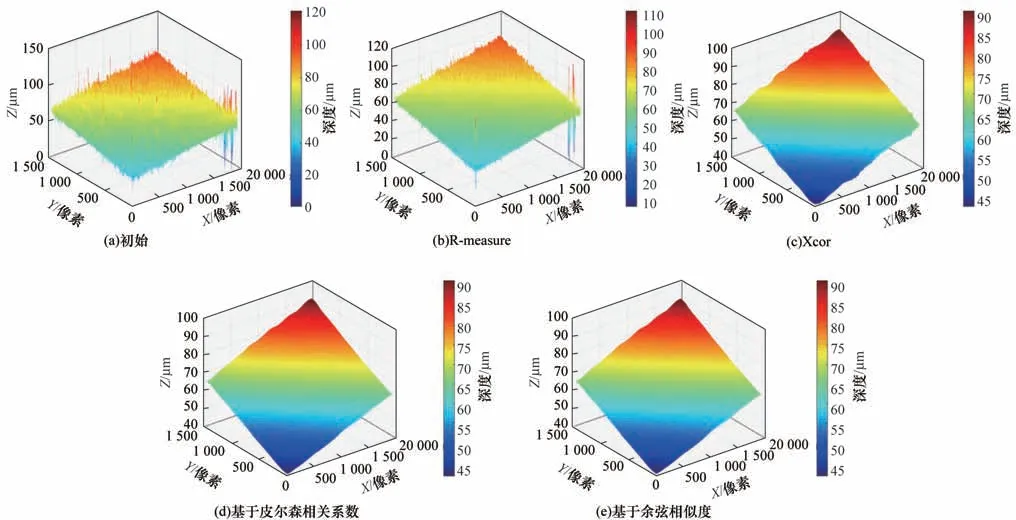
图10 真实斜坡离焦序列图像重建结果Fig.10 Reconstruction results of real slope defocused sequence images

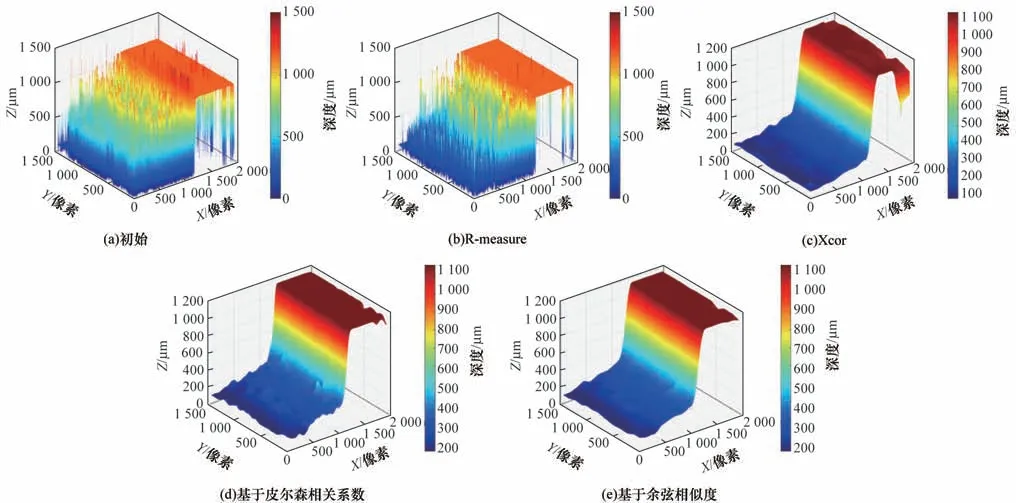
图11 真实台阶离焦序列图像重建结果Fig.11 Reconstruction results of real step defocused sequence images

从图10 可以看出：由于噪声的影响，初始重建结果中存在大量错误估计的深度，斜坡表面深度变化不平滑；R-measure 方法通过可靠性度量剔除了一部分深度估计出错的点，但仍有遗漏，同时在斜坡表面留下了孔洞，造成了深度信息的缺失；Xcor 方法仅仅根据曲线间的相关性对深度图进行优化，没有考虑噪声对灰度曲线的影响，导致在灰度曲线受噪声影响而异常振荡的情况下优化效果变差，边缘处出现错误深度；本文所提方法基于曲线相似度构建引导图，使用引导滤波将其结构信息传输到初始深度图中，优化重建效果，经优化后的重建结果相比于初始深度重建结果有了较大提升，形貌恢复结果中明显的错误深度得到了改善，深度变得更为连续与明显，优于其他方法。

针对图11 这类受噪声影响严重、初始深度图存在大量错误深度信息的图像，R-measure 方法效果有限，并在上表面留下了孔洞，Xcor 方法在上表面边缘处出现了明显错误的深度，而使用本文所提方法进行优化后则仍能得到较为理想的深度结果。

将实验结果与理想重建深度结果进行对比，定量的性能指标如表5 所示，其中最优结果用加粗字体表示。可以看出：在斜坡重建结果中，基于皮尔森相关系数和基于余弦相似度的重建结果相较于初始重建结果在RMSE 指标上分别降低了64.8% 和64.9%，在Corr 指标上都提升了2.18%；在台阶重建结果中，基于皮尔森相关系数和基于余弦相似度的重建结果相较于初始重建结果在RMSE 指标上分别降低了47.3% 和49.8%，在Corr指标上分别提升了6.35%和6.53%。上述实验基于余弦相似度的重建结果均优于基于皮尔森相关系数的重建结果。

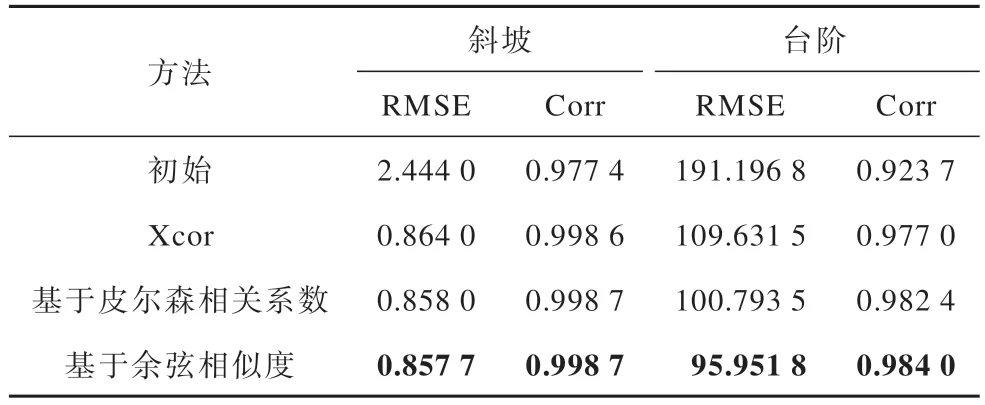
表5 真实离焦序列重建结果评价指标Table 5 Evaluation indexes of reconstruction results of real defocused sequence images

上述实验证实所提方法在真实场景应用中能够提升聚焦形貌恢复的精度，在改善噪声影响的情况下提升三维重建的准确度，得到更完整、平滑的物体三维形貌，即使是初始重建结果较差的情况下，经过深度优化后，仍能得到较为理想的三维重建结果。

4 结束语

本文提出一种基于曲线相似度进行深度图优化的聚焦形貌恢复方法。利用图像灰度曲线与聚焦评价曲线随离焦程度而变化的统一规律，通过曲线间相似性度量方法评估当前像素深度估计的置信度，从而得到整个序列图像深度估计的置信图，并将置信图作为引导图对初始深度进行优化，改善聚焦形貌恢复效果。该方法直接使用图像原始信息，避免了传统方法预处理过程造成的图像信息丢失，能够更好地保留物体原始结构特征。实验结果表明，本文方法能够有效消除噪声的干扰，提高重建精度，恢复出完整连续的物体三维形貌。下一步将对低纹理图像进行研究，提高低纹理或无纹理物体的重建精度。