基于多尺度LDTW 和TCN 的空间负荷预测方法

马越，温蜜

（上海电力大学计算机科学与技术学院，上海 201306）

0 引言

随着社会的不断发展和技术的不断革新，电网的建设正朝着可靠、安全、经济、高效的方向不断前进。城乡建设的飞速发展和人口的大规模流动使得电力负荷的空间分布产生了更迅速的变化，因此也对电网的负荷分布情况分析和负荷预测提出了更高的要求［1-2］。空间负荷预测（SLF）在传统负荷预测的基础上能实现对于供电区域内电力负荷大小和分布情况的预测［3-5］。SLF 不仅反映了该区域内负荷幅值的变化，同时包含了各个小区域的位置分布［6］。SLF 已经成为配电网规划中不可或缺的一部分，为合理建设和使用变电站、馈线等提供了重要的指导［7］。

SLF 一般会将供电区域依据一定的标准分为规则或不规则的小区域，并以各个小区域的区域性质、历史数据、发展规划等特征进行分析来预测负荷的幅值与分布情况［8］。当前主流的SLF 方法主要可分为4 类：趋势法，多元变量仿真法，用地仿真法以及负荷密度指标法。趋势法主要通过小区域的负荷曲线分析未来的负荷分布，但较容易受到环境因素的影响［9-10］。多元变量仿真法对数据的质量要求较高且预测时限较短，主要以经济计量模型对负荷分布进行预测［11-12］。用地仿真法需要对原有区域进行等间距划分，并依此预测小区域的理论负荷值，在结果的检验方面存在一定困难［4，12］。负荷密度指标法一般用于对负荷具有明确功能分类的区域，以包含不同功能的待预测区域作为划分边界，结合地块信息预测各类负荷密度从而得到负荷的分布情况［13-14］，在适应性和准确性上都有较好的表现，因此得到了广泛的使用。

近年来，随着技术的进步，以负荷密度指标法为基本思想的空间负荷预测方法也得到了不断发展，在预测精度逐渐提高的同时仍存在一些有待改进的方面。文献［15］通过最小二乘支持向量机对聚类得到的同类型区域进行负荷分布预测，其中选择的部分样本可能相似度较低从而影响预测效果。文献［16］通过灰色关联分析筛选与待预测区域负荷密度关联度高的样本进行训练，但是模型相对复杂，计算开销较大且由于各个特征之间影响程度不同影响预测结果。文献［17］通过预先评估的密度指标结合区域面积计算地块负荷后进行累加得到预测的负荷分布，但受环境因素的影响较大，且难以确定叠加时的同时率。

综上所述，当前对于SLF 的研究仍面临如下一些挑战：空间负荷预测需要合理利用智能电表采集的用电信息，并与现代城市中的各类信息进行有机结合［9］；随着环境的复杂化，在负荷密度指标的选取和同时率的选择上也提出了更高的要求，以适应不断变化的用地情况［18-19］。

针对上述问题，本文提出一种基于多尺度限制对齐路径长度（LDTW）谱聚类和时间卷积网络（TCN）的空间负荷预测方法。引入多尺度LDTW改进谱聚类的相似性评估指标，提高对于地块负荷所反映出的用电行为的把握。对区域负荷进行详细划分并依据地块特征确定同时率，筛选适合待预测区域的训练样本，并构建基于TCN 的回归预测模型，预测地块负荷密度指标，再基于对应的同时率得到负荷总量，实现空间负荷预测。

1 基于多尺度LDTW 的谱聚类

1.1 多尺度LDTW

用户的电力负荷曲线作为一种典型的时间序列，能直观地反映用户的用电行为习惯。动态时间规整（DTW）是一种广泛用于评估时间序列之间相似性的距离度量，在电力负荷曲线的聚类分析中得到了广泛的应用［20-21］。DTW 的核心思想是通过递归调整曲线之间时间点的匹配与距离计算，从而增强对于曲线整体形状相似性的刻画。但是DTW 对于时间点的调整往往会因为不受限制而产生病态匹配，导致对相似性的分析能力下降［22］。此外，传统的DTW 往往直接通过欧氏距离来评估数据点之间的距离，对于曲线间的距离评估较为片面［23］。

多尺度LDTW 在DTW 的基础上对其存在的缺陷进行了改进，通过限制2 个时间序列之间匹配步长的上限来抑制病态匹配的产生，并从数据点之间的数值距离和斜率距离多个维度提高曲线相似性的综合评估能力。

多尺度LDTW 以更灵活的软约束确定最佳匹配路径。可以反过来观察整个数据点的匹配过程，设路径的总步长为S，匹配过程中的当前步长为s，相应的距离为l。根据DTW 的匹配规则，2 个序列最后一个数据点必须匹配在一起，此时S=s，则最后一步之前的S=s-1 必定来自左侧、下侧或左下侧。由此，添加一个额外的维度来判断上一个数据点的可能步长是在总步长的限制之内。在填充距离矩阵D时，每个位置都需要包含与所有可能的路径相对应的路径长度并选择其中的最小值作为该步匹配过程的记录值。多尺度LDTW 的累积距离矩阵计算过程如式（1）所示：

其中：i、j分别代表序列P、Q上的数据点；s记录当前步长；δ（pi，qj）为数据点在前一个状态的累计距离。

数据点之间数值和导数之差能从不同角度评估曲线的相似性。数值的差异是最直观的差异，直接反映数据点之间的距离，而导数反映了序列的变化趋势是否相似。本文使用数值差分dE（x，y）和导数差分dD（x，y）的组合作为距离度量，并提供可调整的权重α，计算过程如式（2）所示：

数据点pi的导数d（p）i通过式（3）近似计算得到：

如何确定合适的步长限制S是多尺度LDTW 的重要环节。标准差作为评估数据波动情况的一个重要指标，具有计算方便、应用广泛的优点。本文使用标准差来评估负荷曲线的波动，并依此确定步长限制S。通过对比测量数据点与同一位置其他点的标准差来确定是否要在该位置上放宽步长的限制。由此，将原始步长设为负荷曲线本身的长度。计算并记录同一位置点的标准偏差，并将2 个配对点之间的差值与该位置的标准偏差进行比较。当差异较小时，说明该处的波动不足以增加步长；否则，使原始步长将增加1。遍历整个序列，能迭代获得最大限制步长Lmax。

由此，多尺度LDTW 的计算过程如下：

1）构建距离矩阵D［p，q，s］=［累积距离，（p'，q'）］，记录数据点p和q匹配后的累积距离以及前一对匹配点p'和q'的序号。初始化D［1，1，0］=［dis［t1，1，0］，（0，0）］。

2）依据式（1）循环迭代计算距离矩阵D。

3）计算最大限制步长Lmax，在s属于序列初始步长L到Lmax范围内筛选数据点匹配的最后一项D［L，L，s］，取其中的最小值即为2 个序列间的多尺度LDTW 距离。

1.2 谱聚类

谱聚类算法由于其在时间序列聚类中的优秀性能而日益受到关注［24-25］。谱聚类为了实现聚类的目标，通过切割由所有数据点组成的图，并使得最终目标是使切割后不同子图之间的边权重尽可能低，子图内的边缘权重总和尽可能高。通过多尺度LDTW生成负荷曲线的相似度矩阵，取代原有的距离度量。由此，可以得到基于多尺度LDTW 谱聚类的步骤如下：

1）为给定的一组数据点Xi构建一个图G，并使每个数据点成为图中的顶点，通过多尺度LDTW 计算每个样本之间的距离。

2）将得到的距离作为相似性度量计算每一项，形成相似度矩阵MS：

3）构造度矩阵DS。度矩阵DS的每个对角元素是对应的相似度矩阵SS每行元素的总和，所有其他元素都是0。

4）通过相似度矩阵MS和度矩阵DS计算拉普拉斯矩阵LS，对LS进行归一化：

5）计算拉普拉斯矩阵LS的特征向量，并按照特征值的升序重新排列向量形成矩阵H。选择前k个特征向量形成新的矩阵Yk×n。矩阵Y的行向量作为原始负荷曲线的新特征，依此进行聚类，得到聚类结果。

2 TCN

TCN 在CNN 模型的基础上进行了改进，在处理时间序列的问题上具有更加优秀的表现。TCN 能有效分析数据之间存在的关联，且梯度更加稳定，计算效率更高。TCN 充分考虑了电力负荷数据中的时域特征，能根据需要灵活调整输出结点记忆的长短［26-27］。

TCN 主要由膨胀卷积、因果卷积、残差连接等模块构成。膨胀卷积能有选择性地跳过部分输入，其原理是在传统CNN 的感受野中插入空白信息。通过调整膨胀系数d就能控制感受野的大小，调整所接收的信息量。膨胀卷积的计算过程如式（7）所示：

其中：d为膨胀系数；s-d·i为输入序列中的历史数据；k为滤波器系数。

因果卷积保证了TCN 在预测过程中对于目标数据yt所进行的预测只来源于t时刻以及t时刻之前的信息，其原理是通过掩膜的方式将原本全连接的神经元中属于t时刻之后的连接去除，只保留从前往后的连接，使其满足时间上的前后依赖。由此，可以得到膨胀因果卷积结构如图1 所示。

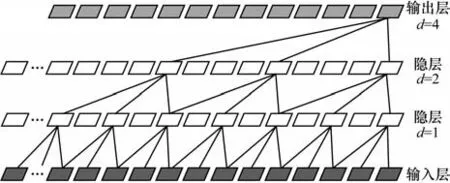
图1 膨胀因果卷积结构Fig.1 Structure of expansion causal convolution

残差连接将输入跳跃连接到输出，从而缓解由膨胀因果卷积造成的网络深度增加所带来的梯度衰退或梯度弥散。

3 空间负荷预测流程

本文提出的基于多尺度LDTW 谱聚类和TCN网络的空间负荷预测流程主要分成4 步：首先通过聚类细化各类型负荷密度指标；其次依据细分的结果划分训练样本并确定各类地块对应的同时率；然后建立回归模型预测小区域的负荷密度；最后将预测结果结合各区域的同时率进行空间负荷预测。

1）精细化负荷密度指标构建。虽然地块本身依据其功能性已经大致划分成了居民负荷、商业负荷、工业负荷、行政办公负荷等几个类别，但是经过观察不难发现，即使是属于同一类型的地块负荷，其负荷曲线所表现出的用电习惯也大相径庭。比如工业负荷的表现就会在很大程度上受到工厂类型的影响，有些工厂主要在白天进行生产作业，有些则需要维持全天不间断运行。对于同一用地性质负荷的细分需要通过基于多尺度LDTW 的谱聚类实现。

2）筛选训练样本并确定同时率。依据基于多尺度LDTW 的谱聚类得到的各类型地块基于用电行为的精细划分，并基于聚类中心提取各类地块的典型负荷曲线。对于待预测区域，选择与典型负荷曲线距离最近的数据作为训练样本。

为每个类型地块确定各自的同时率。同时率的产生来源于庞大电力系统中各用户不同的用电习惯造成的负荷峰值不会出现在同一时间段的现象，因此系统总的最大负荷总是小于各用户最大负荷的直接累加，引入各个类型地块对应的同时率能更加准确地描述负荷之间的关系，提高空间负荷预测的准确性。同时率的计算过程如式（8）所示：

其中：PS为整个划定区域内的最大负荷为各个区域最大负荷之和。

3）建立预测模型。本文采用TCN 网络进行各个区域负荷密度指标的回归预测。根据筛选出的训练样本进行预测，以历史负荷数据等特征作为输入训练模型，将训练模型应用到待预测区域，得到未来负荷的分布情况，并基于此获得各个区域未来的负荷密度指标。负荷密度指标ρi的计算公式如式（9）所示：

其中：Pi为区域负荷预测值；Si为区域面积。

4）整合数据进行空间负荷预测。依据各个地块对应的同时率ηi和预测的负荷密度指标ρi整合预测结果，得到整体区域的未来负荷总量W（设共有N个地块），计算过程如式（10）所示：

其中：ηi为区域对应的同时率；ρi为区域对应的负荷密度指标；Si为区域面积。

由此，便可以得到基于多尺度LDTW 谱聚类和TCN 网络的空间负荷预测的整体流程，如图2所示。

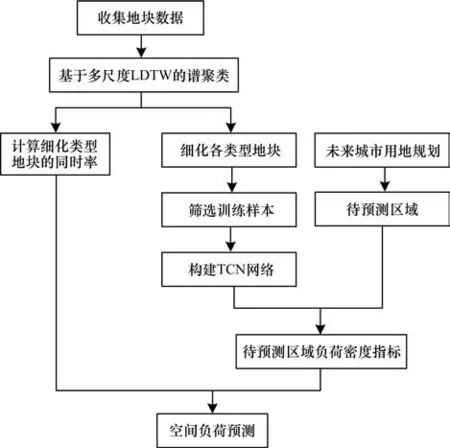
图2 空间负荷预测流程Fig.2 Procedure of spatial load forecasting

4 实验结果与分析

本节将文中提出的空间负荷预测模型在真实数据集上进行实验并与其他经典模型进行对比，综合评估模型的预测效果。

4.1 数据集与评估指标

本文搜集了华东地区某区域内2015 年—2020 年最高负荷日24 点的地块负荷数据样本，共包含313 个地块，涉及居民、工业、商业3 种类型的负荷。记录最大负荷日的负荷曲线与区域的空间信息以及地块类型。数据集基本信息如表1 所示。

表1 数据集信息Table 1 Dataset information

在聚类方面，本次实验主要评估模型对于数据集内各地块负荷曲线的聚类效果，通过DBI 指数和VI 指数2 个评估指标来分析不同方法在数据集上的效果。其中VI 指数相比于传统的聚类评估指标更加聚焦于对负荷曲线数据的聚类效果评估。

其中：Xj为类中的数据点；Ai为类中的中心；T为类中数据点数量；aki为类中对应特征的值；DBI 指数越小，则说明聚类效果越好。

在预测方面，本次实验主要评估模型对于区域负荷预测的准确性，通过绝对误差（EAE）、相对误差（ERE）以及决定系数（R2）3 个评估指标来分析不同方法在数据集上的效果。

其中：y'为预测值；y为真实值。

其中：SSSR为残差平方和；SSST为总变差。

4.2 聚类效果分析

在包含原有地块类型信息的基础上，通过基于多尺度LDTW 的谱聚类对各类型地块进行聚类分析，依据地块负荷的用电行为对负荷进行细分，筛选训练样本，并确定每一类地块的同时率。

为了评估多尺度LDTW 在负荷曲线相似性分析上的有效性，将构成谱聚类的相似度矩阵中的相似性度量替换为欧氏距离、DTW 和Limit DTW 与本文提出的方法进行对比，比较不同相似性度量的聚类效果。DBI 指数与VI 指数结果如表2 所示。

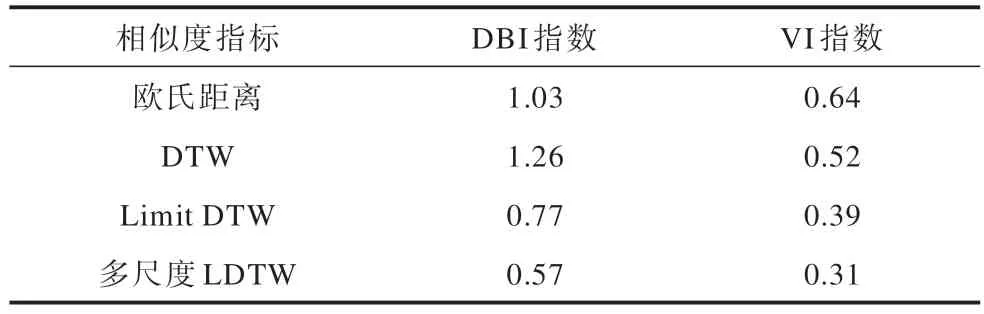
表2 不同相似性度量聚类效果对比Table 2 Comparison of clustering effect in different similarity measures

根据结果对比可知，无论是DBI 指数还是VI 指数，本文提出的多尺度LDTW 的聚类效果均优于其他相似性度量。基于DTW 的聚类虽然在DBI 指数上高于欧氏距离，但是在更聚焦于负荷曲线相似性分析的VI 指数上表现更好，体现了DTW 在时间序列数据分析上的优势。在对DTW 进行改进后的Limit DTW 和本文提出的多尺度LDTW 上，2 个评估指标均明显降低，2 种方法均对DTW 存在的病态匹配问题进行了处理，相比于Limit DTW 通过固定区域来限制匹配的过度错位，多尺度LDTW 提供了更加灵活的柔性限制以寻找最优的相似性描述方案，因而表现更佳。

根据聚类结果，将居民、商业负荷进一步细分为2 类，将工业负荷细分为3 类。由此，可以根据聚类结果得到细分后各个类型地块负荷的典型曲线，从中清晰地观察到不同用户的用电行为习惯。各类型地块典型负荷曲线如图3 所示。

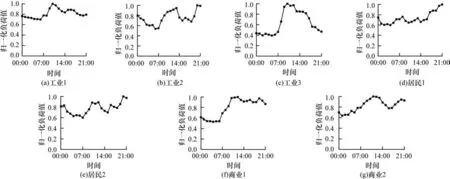
图3 不同类型地块典型负荷曲线Fig.3 Typical load curve of different types of plots

根据结果可知虽然同属于一种类型，不同地块表现出的用电行为存在较大差异。以工业负荷为例：工业1 类型地块负荷波动较小，在白天时段负荷相对较高；而工业2 类型地块呈现双峰特征，在上午时段和晚上负荷较高；工业3 类型地块波动最大，白天的负荷明显高于其他时间。对负荷进行细分筛选训练样本，并基于用电特征确定各自的同时率为后续的预测提供了可靠支持。

4.3 空间负荷预测效果分析

根据聚类细分的训练样本，可以得到细分后的地块分布以及各自对应的同时率如表3 所示。以2015 年—2019 年的地块负荷作为相关历史数据，以2020 年地块负荷作为预测目标，构建预测模型进行预测，就能得到未来各地块最大负荷日的负荷分布情况，再基于最大负荷日的最大负荷确定各个地块的年最大负荷。根据每个地块的面积求取负荷密度，并基于同时率进行聚合得到空间负荷预测结果。

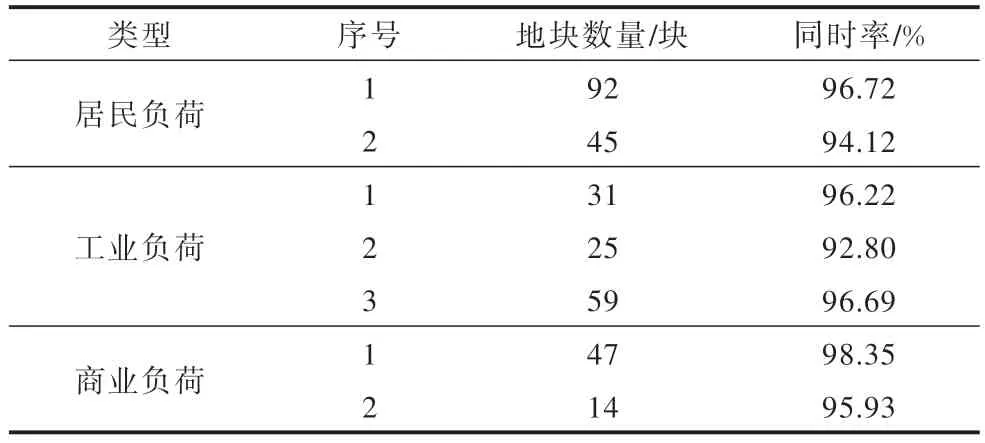
表3 细分地块与同时率Table 3 Subdivided plot and simultaneity rate

为了评估TCN 在负荷预测过程中的有效性，对比其与LSTM、GRU 和ResNet 的预测效果，得到的绝对误差、相对误差以及决定系数如表4 所示。

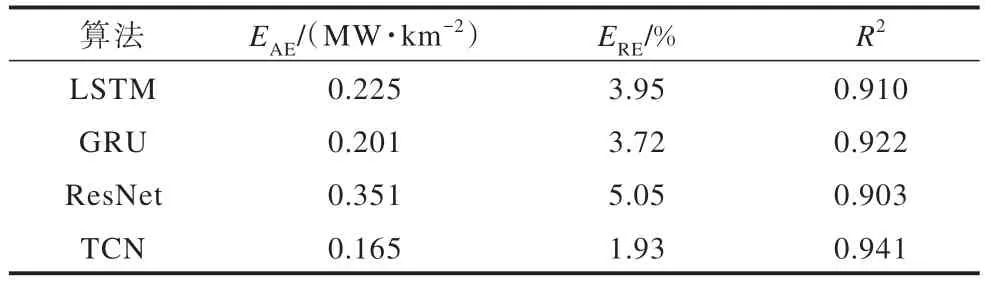
表4 不同算法预测效果对比Table 4 Comparison of forecasting effect in different algorithms

根据结果对比可知，TCN 的表现优于发源于RNN 的典型的时间序列预测算法LSTM 和GRU，以及同样发源于CNN 的ResNet。TCN 能更好地控制模型的内存大小以适应不同的域，同时提供了更稳定的梯度。TCN 在空间负荷预测中预测效果良好。预测的负荷值与实际负荷值对比曲线如图4 所示。

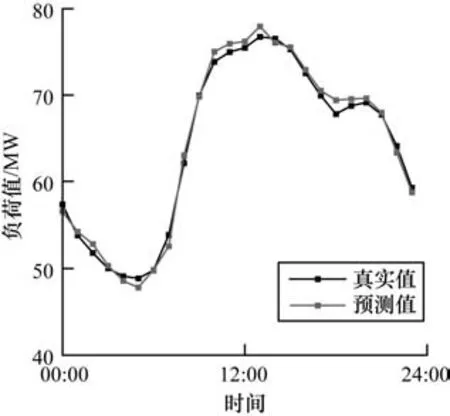
图4 预测负荷值与实际负荷值对比Fig.4 Comparison of predicted load value and actual load value

将本文提出的方法（方法1）与传统的负荷密度指标法（方法2）以及文献［5］（方法3）和文献［16］（方法4）中的方法进行对比。传统的负荷密度指标法根据经验值确定各类型地块的负荷密度并基于固定的同时率进行聚合，文献［5］通过模糊C 均值聚类细分地块负荷，并通过极限学习机进行预测。文献［16］则通过灰色关联度分析筛选训练样本，并构建LSSVM 模型预测地块负荷。不同空间负荷预测方法得到的预测结果如表5 所示。

表5 不同空间负荷预测方法对比Table 5 Comparison of different spatial load forecasting methods

本文方法与其他典型的空间负荷预测方法相比在预测效果上仍然表现良好。方法2 由于是直接通过经验值进行简单聚合计算，因此计算速度明显快于其他方法，但相对而言其预测精度就大打折扣，通过查表确定的经验值会受到地块特征的影响产生较大偏差，因此该方法只适用于粗略的估算。方法3 和方法4 的预测精度均低于本文提出的方法，但是在运行时间上略快。相比于方法3 和方法4，本文的聚类分析和负荷预测都更加聚焦于负荷数据的时间特性，在分析过程中充分考虑了数据的时间关联性，因而在预测精度上高于其他方法。此外，本文提出的方法还针对不同地块类型提供了不同的同时率，削弱了负荷峰值出现时间不一致所带来的误差影响。综上所述，本文提出的方法虽然牺牲了一定的计算效率，但是在空间预测精度方面得到了较大提升，验证了本文提出方法的有效性。

5 结束语

本文提出一种基于多尺度LDTW 和TCN 网络的空间负荷预测方法。以改进的多尺度LDTW 评估地块负荷曲线的相似性，更加准确地分析地块的用电行为，对已确定土地使用性质的区域进行精细划分，筛选训练样本，并分别确定同时率。基于划分的样本构建TCN 网络预测模型，得到负荷密度指标，基于区域面积以及对应同时率进行空间负荷预测。实验结果表明，该方法的预测效果良好，具有较强实用性。下一步将考虑缩减模型的计算开销，在保证预测精度的同时提高计算效率。