基于因果自回归流模型的因果结构学习算法

卢小金，陈薇，郝志峰，2，蔡瑞初*

（1.广东工业大学计算机学院，广东 广州 510006；2.汕头大学理学院，广东 汕头 515063）

0 引言

许多科学研究的目的为揭示某些事物的因果关系，进而找到支配它们的规律［1］。干预或随机实验是发现因果关系的传统方法［2-3］，然而通常存在高成本、高耗时甚至无法实现等问题。因此，通过分析观察数据来揭示事物因果信息，也被称为因果发现的相关研究近年来引起了很多关注［4］。

在过去的几十年里，因果发现研究已经取得了一系列跨学科的进展，被广泛应用于生态学、生物基因学、流行病学、神经科学等领域［5］。同时，一系列识别因果效应的算法被提出［6-8］，典型的方法有基于约束［9-10］、基于评分［11］和基于梯度优化［12-13］的因果学习算法，以及一些混合因果结构学习算法［14-15］。其中：基于约束或评分的算法存在无法识别等价类的问题；基于梯度优化的算法可解决等价类识别的问题，但通常依赖于加性噪声项和原因变量互相独立的因果函数模型假设。

KHEMAKHEM等［16］于2021 年提出了因果自回归流模型（CAREFL），该模型基于仿射自回归流拓展了现有的非线性函数因果模型，在结果变量的噪声项与原因变量不独立时仍然是可识别的，但只能识别两个变量的因果对，无法学习高维变量下的因果网络结构。针对加性噪声项受原因变量影响的多维变量因果网络学习问题，本文结合基于约束的因果骨架学习方法和因果自回归流函数模型，提出一种混合因果结构学习算法。该算法从完全无向图出发，基于条件独立性得到典型因果骨架，进而基于CAREFL 计算备选方向的边缘似然度进行因果方向推断。

1 相关工作

非时序观察数据的因果发现方法主要包括基于约束的因果发现方法、基于评分的因果发现方法和基于梯度优化的因果发现算法。基于约束的方法包括PC 算法［9］和FCI 算法［10］。PC 和FCI 算法基于条件独立性检验的方法，虽然能够在满足算法前提的情况下近似准确地学习到因果结构，但因为马尔可夫等价类的存在（不同的因果结构可以满足同样的条件独立性），两者都无法确保输出全部的因果信息。针对没有混淆因子的场景，基于评分的方法通过优化合理定义的评分函数来找到具有完整因果信息的结构，经典的方法有GES［11］算法。基于梯度优化的因果发现方法，如NOTEARS［12］和GOLEM 算法［13］，由于对数据分布做了额外的假设而不仅是基于条件独立关系，因此能够区分同一等价类中的不同因果结构。基于梯度优化的方法一般需要依赖某类函数因果模型（也被称为结构方程模型）来保证因果可识别性（最优结构存在且唯一）。

函数因果模型主要分为线性模型和非线性模型。经典的线性模型为线性非高斯加性模型（LiNGAM）［7，17］。LiNGAM 对数据的生成方式做了线性和非高斯独立噪声的假设，并利用独立成分分析进行求解。经典的非线性函数因果模型有加性噪声模型（ANM）［6］和后非线性模型（PNL）［8］。该类模型对数据生成方式做了非线性和独立噪声的假设。在LiNGAM、ANM、PNL 等模型中，均要求加性噪声项和原因变量独立以保证模型的因果可识别性。CAREFL 基于噪声项和父母结点独立的假设，将加性噪声模型进行拓展，使得模型在加性噪声项与原因变量不独立时仍然能够识别变量之间的因果方向，但只讨论了二维变量的因果方向推断场景，无法解决多维的因果结构学习问题。

2 问题定义

本节对所研究问题进行符号化定义和说明。

定义数据集D中包含n个可观测变量的集合V={V1,V2,…,Vn}，样本量大小为m。令数据集D蕴含的因果结构为有向无环图G={V,E}，其中，E={(Vi,Vj)|Vi→Vj,Vj↛Vi}表示G中结点间边的集合。Vpa（j）表示Vj的所有 的原因结点，即若Vi∊Vpa（j），则Vi→Vj。同时假设满足因果忠诚性假设：数据集D的分布P忠诚于因果图G。这表明，对于任意的Vi,Vj∊V(i≠j)和集合s∊V，给定，如果Vi和Vj在集合s中的变量的条件下独立，则Vi和Vj被集合s中的变量d-分离［18］。由于因果忠诚性假设保证了分布中的条件独立性和因果图的一致性，因此能够利用基于条件独立性的方法得到因果图的骨架。

基于上述符号说明和假设，本文关注的是典型因果网络学习问题，其定义如下：给定具有n个变量V={V1,V2,…,Vn}的数据集D，基于因果忠诚性假设，如何学习变量集V的因果结构。

3 基于CAREFL 的因果结构学习算法

针对因果网络学习的目标，本文提出一种基于因果自回归流模型的混合因果结构学习算法，简称SCARF 算法。图1 给出了SCARF 算法的整体框架。该算法框架分为两个阶段：第一个阶段基于无向完全图，通过条件独立性删除不存在因果关系的变量之间的边，得到因果骨架图；第二个阶段基于因果自回归流模型，分别对骨架图中的每一条无向边进行因果方向推断。

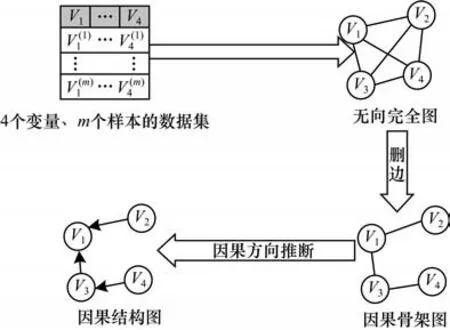
图1 SCARF 算法框架Fig.1 Framework of SCARF algorithm

3.1 因果骨架学习

受基于约束的方法启发，本文考虑使用条件独立性检验来判断变量之间是否存在因果边。首先从无向完全图出发，对每个结点及其邻接结点进行独立性检验，删除不存在因果关系的结点之间的边。因果骨架学习的算法伪代码如算法1 所示。

算法1基于条件独立性学习因果骨架

算法1包含了3 层关键的循环：第1 层循环的作用是从条件集的空集开始遍历，逐个增加条件集个数，从而找到使得变量独立的最小条件集；第2 层循环遍历所有满足条件|adj(C,Vi){Vj}|≥Llength的无向边(Vi,Vj)，寻找是否有使得Vi和Vj独立的条件集，因为对于(Vi,Vj)而言，其条件集只会出现在Vi的邻居中，因此此判断条件可加快遍历条件集的速度；第3 层循环的作用是对于Vi的邻接结点遍历长度为Llength的所有组合，进而将每个组合作为条件集，检验Vi与Vj的独立性，删除检验结果为条件独立的边。

在本文算法中，需要对有限的样本评估条件独立性，做法是首先计算样本偏相关系数，利用Fisher转换得到偏相关系数的概率分布，进而基于假设检验进行独立性测试。文献［10，19］为该独立性检验方法的可靠性提供了理论证明。

3.2 因果方向推断

在得到由无向边构成的因果骨架后，需要对无向边进行因果定向。在基于结构方程模型的因果发现算法中，由于需要具备因果关系可识别性和计算可实践性，结构方程模型通常具有特定的形式，如被广泛使用的加性噪声模型：

其中：fj是关于Vj的原因变量的非线性函数；nj是Vj对应的加性噪声项，各个变量对应的噪声独立同分布。ANM 模型将关于原因变量的非线性函数与其噪声项相加，简洁高效，但在加性噪声项与父母结点不独立的场景下，无法保证因果可识别性。KHEMAKHEM等［16］提出的因果自回归流模型则弱化了加性噪声模型的假设，使其在因果方向判断上也具备可识别性。

3.2.1 自回归标准化流

在介绍因果自回归流模型前，先介绍标准化流。标准化流基于隐变量z∊Rn，通过一系列可微可逆的变换T表达观测数据V∊Rn的分布。z通常是简单的基分布pz(z)，从而可以基于变量转换获得V的分布：

其中：T或者T-1通常使用神经网络实现。为了提高网络拟合能力和保持变换的可逆可微性质，标准化流模型通常将同族的一系列映射T1,T2,…,Tk链接起来，从而使得T=T1◦T2◦…◦Tk。同时，T的雅克比矩阵行列式|detJT-1(V)|可以从子变换Tl的行列式计算中得到。因此，在设计标准化流模型时，研究者需要考虑的重要因素就是Tl雅克比矩阵行列式的计算复杂度。

自回归流模型［20-22］固定变量的输入顺序，以及设计特定的模型结构将雅克比矩阵限制为下三角矩阵以达到简化行列式计算的目的。自回归流模型结构包括简单的加法和仿射变换［23］，以及更复杂的神经样条变换［24］。在文献［22］中，自回归流模型的转换函数T表示如下：

其中：π是关于V中变量自回归结构的排列；V＜π（j）表示在π中排在Vj之前的变量；函数τ（j也被称为转换器）相对于 第一个参数zj是可逆 的并且由V＜π（j）参数化。

3.2.2 因果自回归流模型

结合上文可以看到式（1）和式（3）的高度相似性，这体现在两个模型都显式定义了基于变量的某种结构或顺序。鉴于这个相似性，基于自回归流模型构造的函数因果模型CAREFL 被提出：

其中：zj是噪声变量，各结点的噪声变量是独立同分布 的；Vpa（j）是在图G中的Vj的父母结点；tj和uj是 任意函数。在CAREFL 模型中，噪声项不是简单地与关于原因变量的非线性函数相加，而是可以受到原因变量的调控，这更符合现实场景。特别地，在各变量的t均为0 的情况下，式（2）是加性噪声模型［见式（1）］的一部分。

假设因果顺序为Vi→Vj，结合式（2）和式（4），可以得到因果自回归流模型的边缘对数似然度：

3.2.3 基于流模型的似然度比较

对因果骨架中的某条无向边定向，实际上是在Vi→Vj和Vj→Vi两个备选模型中选择其一。本文利用标准化流分别拟合备选模型。对于某个备选方向，使用极大似然度的方法去优化每一层流中神经网络的参数。为了避免过拟合，将样本切分为测试集和训练集，用训练后的模型评估测试集的似然度。综上所述，因果方向判断的数学形式被定义为：

4 SCARF 算法描述

结合算法1 中基于约束的方法和标准化流技术，本文提出SCARF 算法。SCARF 算法伪代码详见算法2。SCARF 算法分为两个阶段：第一个阶段是通过算法1 得到均为无向边的因果骨架（第1 行）；第二个阶段是遍历因果骨架中的所有边（第3～14 行），基于标准化流技术，通过极大似然法优化模型中神经网络的参数，通过比较边缘似然度的经验期望（第8～13 行）进行因果方向推断。最终，算法输出的是表征变量间因果信息的有向无环图。

算法2SCARF 算法

5 实验与结果分析

为了验证SCARF 算法在因果结构学习上的有效性，本节对该算法在仿真因果结构数据集和真实因果结构数据集上的实验效果进行分析和评估。在评估实验中，本文选取的对比方法有基于条件独立性的约束算法PC、基于函数因果模型的ICALINGAM 和GOLEM。对于随机生成和真实的因果结构，实验数据的生成机制服从如下非线性结构方程：

其中：ui～N(0,1) 是随机生成的噪声变量；ai～U(-2,-0.5)∪(0.5,2)与bi～U(-2,-0.5)∪(0.5,2)是每个父母结点对Vi的随机因果权重。每组实验的运行次数在40 次以上。采用F1 值作为因果结构学习的评价指标，计算公式如下：

其中：TP表示因果结构图G中方向预测正确的边数量；FP表示将反向预测成正向的数量；FN表示将正向预测成反向或无向的数量。

5.1 仿真因果结构数据集实验

通过4 个方面的控制变量实验评估SCARF 算法的性能。每组实验都根据实验参数随机生成因果结构和数据，实验参数设置如下：在数据生成机制实验组中，控制变量是加性噪声项是否与原因变量独立（默认加性噪声项不与原因变量独立），结点维度有10、16、20、30，因果图的平均入度有0.5、1、1.5、2，样本大小有500、1 000、2 000、3 000、4 000、5 000，其中，加粗字体为默认实验参数。

为了对比SCARF 在噪声项和原因结点独立时的结构学习性能，本文引入了噪声项不受父母结点调控的实验效果，其数据生成机制服从以下结构方程：

其中：wjl～U(-2,-0.5)∪(0.5,2),l=1,2,3，是每个父母结点对Vi的随机因果权重，此时加性噪声项ui不受父母调控。同时，对照组根据式（7）生成噪声项受父母结点调控的数据。

图2 给出了噪声项是否受父母结点调控的仿真实验结果。从图2 的结果可以看到，无论加性噪声项是否受到原因变量的影响，SCARF 算法的F1 值都显著高于对比方法，保持在0.74 以上。同时，在加性噪声项受到原因变量影响的场景中，基于条件独立性的PC 算法指标没有受到显著影响。基于函数因果模型的GOLEM 和ICALINGAM，F1 值较低并且指标下降趋势更明显。这是因为GOLEM 基于ANM 模型，ICALINGAM 基于LiNGAM 模型，两者都属于加性噪声模型，在噪声项与原因变量不独立时会破坏两者的因果可识别性。实验结果表明，基于因果自回归流模型的因果推断方法不仅适用于现有的加性噪声模型，在噪声项受父母结点影响时依然能够识别因果方向，拓展了加性噪声模型的应用场景。

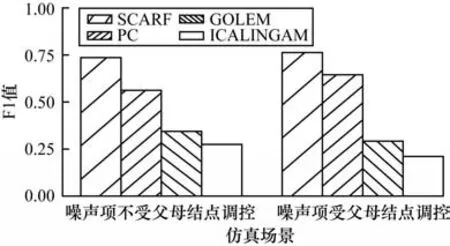
图2 不同因果机制仿真数据的实验结果Fig.2 Experimental results of different causal mechanisms simulation data

在图3 中，实验的控制变量是结点的维度。可以看到，随着结点维度的增加，所有算法的指标都有不同程度的下降，绝大部分因果算法对结构结点都有一定敏感度。但本文算法在这10、15、20、30 这4 个结点维度下，结构学习的F1 值始终维持在0.73 以上，显著高于对比算法，这验证了本文算法的鲁棒性。

图3 不同的结点维度下的实验结果Fig.3 Experimental results at different node dimensions

图4 给出了控制变量为平均入度的实验结果。随着结构的平均入度增大，因果图更加稠密，结构学习难度会增大。实验结果也表明随着平均入度增大，所有算法的F1 值都有不同程度的下降。本文算法的F1 值维持在0.71 以上，高于所有对比方法的最高值。这说明本文算法对结构平均入度有一定敏感度，但是依然能够保持较强的结构学习能力。

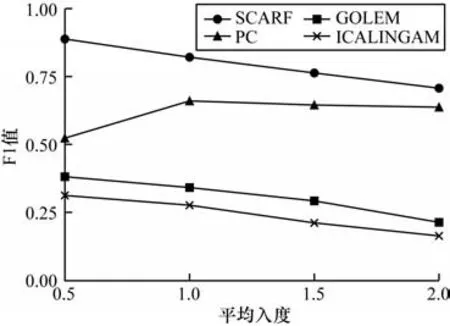
图4 不同平均入度下的实验结果Fig.4 Experimental results at different average in-degrees

图5 给出了不同样本数量下的实验结果。可以看到，大部分算法对样本数量较为敏感，但当样本规模提高到一定数量后，F1 值保持平稳波动。SCARF 在样本数量达到1 000 个后，F1 值在0.74 以上保持波动，高于其他对比方法的最高值，这是因为标准化流对分布具有强大的拟合能力，对样本数量敏感度较低。

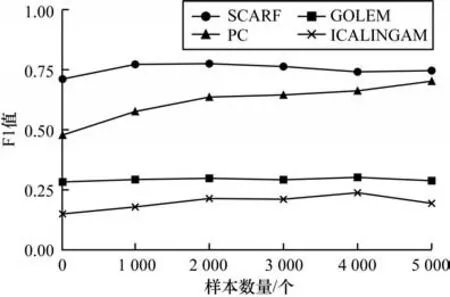
图5 不同样本数量下的实验结果Fig.5 Experimental results at different sample sizes

5.2 真实因果结构数据集实验

从https：//www.bnlearn.com/bnrepository/中选取4 个真实因果结构进行实验，验证本文算法在真实因果结构下的学习能力，这4 个真实因果结构的信息如表1 所示。

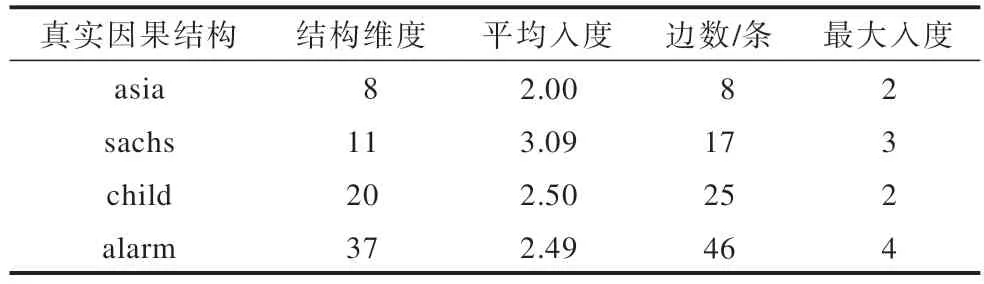
表1 真实因果结构信息Table 1 True causal structure information

在真实结构的数据集中，根据式（7）生成样本数量为3 000 的数据集。在图6～图8 中分别比较了各算法在4 个真实因果结构上的F1 值、召回率和准确率。图6 表明，SCARF 在真实因果结构上的F1 值显著优于对比方法，F1 平均值比ICALINGAM 高出48%。SCARF 对于不同的因果结构的F1 值在0.7 以上，相对稳定，这验证了SCARF 在真实因果结构中的鲁棒性。在图7 和图8 中，对比方法中基于函数因果模型的ICALINGAM 和GOLEM 的准确率很高但召回率却很低，这是因为在噪声项受原因变量影响的场景下，不符合这两个算法的可识别性前提，导致结构中许多父母结点的信息无法识别。

图6 真实因果结构数据集中不同算法的F1值Fig.6 F1 scores of different algorithms in true causal structure dataset

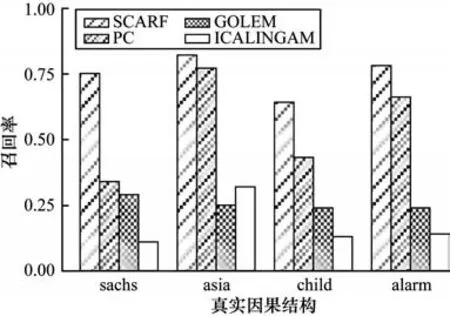
图7 真实因果结构数据集中不同算法的召回率Fig.7 Recall of different algorithms in true causal structure dataset

图8 真实因果结构数据集中不同算法的准确率Fig.8 Accuracy of different algorithms in true causal structure dataset

6 结束语

本文提出一种基于结构因果自回归流模型的因果网络学习算法SCARF，通过结合传统的基于独立性检验的因果骨架学习方法以及因果自回归流模型，解决噪声项受父母结点影响场景下的因果网络学习问题。在虚拟因果结构数据集和真实因果结构数据集上的实验结果表明，SCARF 算法较对比算法召回率更高、鲁棒性更强。实验中的真实因果结构来自于生物、医学等领域的经典数据集，这表明SCARF 具备在实际应用场景中进行因果发现任务的能力，可应用于神经科学、生物信息学等领域。本文算法中对于网络的全局搜索依赖于传统的条件独立性方法，随着结点维度增大，算法的时间效率会受到约束，下一步将研究如何利用标准化流中神经网络可使用反向梯度传播的属性，基于梯度优化学习全局网络的算法，达到提升算法的使用范围和降低时间复杂度的目的。