高效的一次性弱间隙序列模式挖掘算法

杨鸿茜，武优西*，耿萌，刘靖宇，李艳

（1.河北工业大学人工智能与数据科学学院，天津 300401；2.河北工业大学经济管理学院，天津 300401）

0 引言

随着大数据的发展和应用，如何高效地挖掘出数据背后的潜在信息并将这些信息整合利用到更深层次的研究中变得尤为重要。序列模式挖掘（SPM）［1-2］作为数据挖掘［3-4］领域的一个重要子课题，被广泛应用于脱氧核糖核酸（DNA）检测［5-6］、生物遗传学［7-8］、文本检索［8-9］、股票预测［9-10］等领域。

传统的SPM 方法［11-12］只考虑模式在序列中是否出现，而忽略了模式的重复性。因此，为了更加灵活地应对用户的挖掘需求，发现更有价值的模式，带间隙约束的可重复SPM 方法应运而生。根据模式的出现形式可以将其分为4 种情况，即无特殊条件［13］、无重叠条件［14-15］、不相交条件［16-17］和一次性条件［18-19］。其中，一次性条件［20-21］是指序列中的任何项目只能被模式匹配一次，这种约束条件既规避了结果集爆炸的问题，又尽可能地避免遗漏重要的信息。

在传统的间隙约束序列模式挖掘中，模式的每一项都被认为具有相同意义，这与实际情况是不符的。比如，商人会更关注高利润的商品，股民会更关注波动较大的股票市场信息。因此，弱间隙约束的概念被提出并用于序列模式挖掘领域，即仅挖掘那些用户更感兴趣的项，而忽略其他不重要的项。文献［22］提出了一次性弱间隙强模式挖掘（OWSP-Miner）算法，可以实现在单项序列中挖掘一次性自适应弱间隙强模式。

但是上述算法只能在一种特殊序列中进行挖掘，即单项序列。实际生活中的通用序列由若干项集组成，每个项集都包含许多有序的项，即项集序列。在项集序列中研究此问题更有价值和实用性。本文提出一次性弱间隙序列模式挖掘（OWP）算法，该算法在更具通用性的项集序列上高效挖掘一次性弱间隙强模式。首先区别于单项序列上的一次性定义，重新定义一次性条件以适用于项集序列的情况，在支持度计算方面，提出SupII 算法，采用倒排索引的数据结构避免重复扫描数据库，提高算法的匹配效率。然后在候选模式生成部分，采用模式连接策略，减少冗余候选模式数量。

1 相关工作

自序列模式挖掘的概念被提出以来，其广泛应用于大数据挖掘、文本分析、生物信息学等诸多领域［23-24］。近年来，由于带间隙［25］的模式更具灵活性并且能够考虑模式在序列上的重复性，相关研究的重点不断向间隙约束序列模式挖掘靠拢。文献［26］提出一种有效的方法来挖掘具有间隙约束的完整闭合序列模式；文献［27］提出基于通配符约束的生物序列模式挖掘算法，使用单向扫描和双向扫描相结合的方式在生物序列中挖掘带有通配符的频繁模式；文献［28］提出一个挖掘框架，可以在物联网设备产生的不确定数据集中挖掘潜在的高平均效用模式；文献［29］将具有特定间隙数的序列模式挖掘方法应用于DNA 序列。

然而，在上述算法中，所使用的数据集的每一项都被认为是具有相同意义的。而在实际应用中，用户对于不同的项目感兴趣程度也是不同的。因此，文献［30］提出一种基于弱间隙的模式挖掘算法，根据影响程度将项目集划分为强项集合和弱项集合，仅挖掘那些用户更感兴趣的强模式。虽然该算法的效率很高，但它没有关注到序列项目使用的重复性，并且可能造成结果集爆炸的问题。为了避免该问题，文献［22］提出OWSP-Miner 算法，该算法挖掘一次性条件下自适应弱间隙强模式，一次性条件既可以有效减少冗余模式的产生，又充分考虑到了模式在序列上的重复性。

然而，OWSP-Miner 只能在单项序列上进行挖掘，并不适用于通用的项集序列。因此，本文提出OWP 算法来挖掘频繁的一次性弱间隙强模式。

2 相关定义

定义1（序列数据库）序列数据库是一个包含k条序列的集合，表示为D=｛s1，s2，…，s｝k。T=｛t1，t2，…，t｝c是数据库D中所有项的集合，其中，c是T的大小。D中的每条序列都是一个包含若干个项集的列表，表示为si=si1，si2，…，sin，其中，n为序列si的大小，表示为size（si）=n。每个项集sij都是集合T的一个有序子集，用lij=len（si）j表示项集的长度，序列的长度是它所包含项集长度的总和，即

定义2（强项集合和弱项集合）所有的项根据用户感兴趣程度分为强项集合（τ）和弱项集合（ω），并且τ∩ω=∅,τ∪ω=T。

例1给定一个项集序列数据库D如表1 所示，其 中，s1=（bc）（bef）（abce）（abd）（abd）（cf）（adf），可知，T=｛a，b，c，d，e，f｝，size（s1）=7，len（s1）=20。如果强项集合为τ=｛a，b，d，e｝，那么弱项集合就为ω=｛c，f｝。

表1 项集序列数据库DTable 1 Itemset sequence dataset D

定义3（弱间隙强模式）大小为r的弱间隙强模式可表示为p=p1*p2*…*pr，其中，pi⊆τ（1 ≤i≤r），*表示任意数量的弱项集。

定义4（出现和一次性出现）给定序列s=s1，s2，…，sn和一个模式p=p1*p2*…*pr。如果存在r个整数o=满足pi⊆,1 ≤i≤r,1 ≤o1＜o2＜…oi＜…＜or≤n，并且oi-1和oi之间的任一项集都是弱项集，那么o=被称为模式p在序列s上的一个出现。给定模式p在s上的另一个出现o'=，如果满足对任意q和t，若，那么就称o和o'是模式p在序列s上的2 个一次性出现。

定义5（支持度）弱间隙强模式p在序列si上满足一次性条件的出现次数就称作模式p在序列si上的支持度，表示为sup（p，si）。模式p在序列数据库D上的支持度是模式p在D中各条序列上的支持度之和，即

例2给定序列s1=（bc）（bef）（abce）（abd）（abd）（cf）（adf）和一个弱间隙强模式p=（b）*（b）*（ad）。如果忽略弱间隙约束，那么因为p1=（b）⊆s1=（bc），p2=（b）⊆s2=（bef），p3=（ad）⊆s4=（abd），则<1，2，4>是模式p在s1上的一个出现。然而，当τ=｛a，b，d，e｝，ω=｛c，f｝时，<1，2，4>就不是一个出现，因为s3=（abce）中存在强项，所以<1，2，4>不满足弱间隙约束。显然，<2，3，4>、<3，4，5>和<4，5，7>是模式p满足弱间隙约束的全部出现。其中，<2，3，4>和<3，4，5>不满足一次性条件，因为p1∩p2=b≠∅并且索引3 在两次出现中被重复使用，即项集（abce）中的项'b'在出现<2，3，4>中与p2匹配，在出现<3，4，5>中又重复与p1匹配。尽管<2，3，4>和<4，5，7>也重复使用了s4，但是在<2，3，4>中，使用的是s4=（abd）中的项'd'，而在出现<4，5，7>中，使用的是s4=（abd）中的项'b'，因此它们是满足一次性条件的两个出现。综上所述，一次性弱间隙条件下p的所有出现为<2，3，4>和<4，5，7>，即p在序列s1上的支持度为sup（p，s1）=2。同理，sup（p，s2）=1，sup（p，s3）=0。根据定义5，模式p在序列数据库D中的支持度为

定义6（频繁模式）给定一个最小支持度阈值minsup，如果一个弱间隙强模式p在序列数据库D上的支持度不小于minsup，那么模式p就被称为一个频繁的一次性弱间隙强模式。

例3在例2 中，若给定minsup 为3，则模式p=（b）*（b）*（ad）是一个频繁的一次性弱间隙强模式，因为其在表1 所示的项集序列数据库中的支持度sup（p，D）=3≥minsup。

定义7（一次性弱间隙序列模式挖掘）给定项集序列数据库D、弱项集合和最小支持度阈值minsup，一次性弱间隙序列模式挖掘的研究目标是挖掘序列数据库D中所有频繁的一次性弱间隙强模式。

3 算法描述

3.1 准备阶段

为了在后续计算支持度的过程中减少对原始数据的遍历次数以及无用候选模式的生成，准备阶段主要有2 个步骤：创建倒排索引和剪枝不频繁的项以获得1 长度的频繁模式集合。

步骤1扫描序列数据库以获得所有项的集合，并为每个序列创建各自的倒排索引。

定义8（倒排索引）对包含k条序列的序列数据库D，创建k个倒排索引I=｛i1，i2，…，ik｝。倒排索引ij对应序列sj，如果sj有h个不同的项，那么倒排索引ij=｛k1∶v1，k2∶v2，…，kh∶vh｝，其中，键k（a1≤a≤h）存储的是项，而值va存储的是项ka出现位置的列表。

例4给定序列s1=s1s2s3s4s5s6s7=（bc）（bef）（abce）（abd）（abd）（cf）（adf）。以 项'a'为 例，不难发 现'a'出现在序列中的第3 个项集、第4 个项集、第5 个项集以及第7 个项集中，因此，项'a'的倒排索引为［3，4，5，7］。同理，可以得到该序列相应的倒排索引为：i1=｛'a'：［3，4，5，7］，'b'：［1，2，3，4，5］，'c'：［1，3，6］，'d'：［4，5，7］，'e'：［2，3］，'f'：［2，6，7］｝。

步骤2依次计算每个强项的支持度，如果该项的支持度小于minsup，则对其进行剪枝。此外，剪枝所有弱项，因为弱间隙约束规定弱项只允许出现在间隙中，而不可以构成模式。

例5在例4 中，假设在s1中挖掘1 长度的频繁模式，若minsup 为3，τ=｛a，b，d，e｝，ω=｛c，f｝，则强项'e'被剪枝，因为它的支持度为2。尽管项'c'和'f'的支持度都为3，但它们依然要被剪枝，因为它们是弱项。

3.2 支持度计算

在第3.1 节中，通过创建倒排索引和剪枝得到了长度为1 的频繁模式集合。关键问题是计算长度为m（m≥2）的模式p在序列s中的支持度。基于模式中各项的出现位置，提出SupII算法来计算长度为m（m≥2）的模式的支持度。SupII 算法主要分为5 个步骤。

步骤1给定长度为m（m≥2）的模式p=e1，e2，…，ej，…，em（1≤j≤m，ej⊆τ）。首先为模式p所使用的倒排索引创建m层节点。

例6给定一 个弱间 隙强模式p=（b）*（b）*（ad），由例4 可知，模式p中包含的项'a'、'b'和'd'的倒排索引分别为'a'：［3，4，5，7］、'b'：［1，2，3，4，5］、'd'：［4，5，7］，则创建4 层节点如图1 所示。

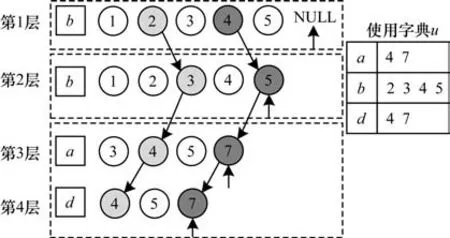
图1 模式p 在序列s1中的所有出现Fig.1 The supports pattern p in sequence s1

步骤2为了保证一次性条件，创建并初始化使用字典u以记录不同项被使用过的位置。使用字典中的每个元素都由两个部分组成：键和值。键存储项，值存储对应项被使用过的位置索引。

比如，当计算模式p=（b）*（b）*（ad）的支持度时，初始化使用字典u为｛'a'：［］，'b'：［］，'d'：［］｝。

步骤3按照p=e1，e2，…，ej，…，em（1≤j≤m，ej⊆τ）从左往右的顺序，从第1 层的每一个未被使用过的位置开始，自上而下寻找模式p所有满足一次性弱间隙约束的出现。对于所有的eu…e（v1≤u≤v≤m）可分为以下2 种情况：

1）若eu…ev在同一个项集内，则对于所有的ej（u≤j≤v），出现位置相同。

2）若eu…ev在不同项集内，则根据项集的先后顺序，出现位置也保持相应的先后顺序，并且不同项集间满足弱间隙约束。

例如，在图1 中，1 是第1 层中第1 个没有被使用过的位置，于是在第2 层中寻找大于1 且未被使用过的位置，即2。继续在第3 层寻找大于2 且未被使用过的位置，得到位置3。但是，在同一个项集内的第4 层中没有找到位置3。因此，位置3 被舍弃，回溯到第3 层的下一个位置4。然而，在位置2、4 中，即s2和s4之间存在强项s3=（abce），不满足弱间隙约束，因此，需要回溯到第2 层，寻找第2 层中下一个未被使用的位置3。此时，位置1、3 也不满足弱间隙约束，于是继续回溯到第1 层找到下一个位置2。按照同样的方法向下迭代，可以找到模式p的一次出现<2>、<3>、<4，4>，即<2，3，4>。

步骤4得到模式p的一次出现后，需要在使用字典u中更新当前已使用过的位置。

例如，在获得模式p的第1 个出现<2，3，4>后，更新使用字典为u=｛'a'：［4］，'b'：［2，3］，'d'：［4］｝，因为（b）、（b）和（ad）分别对应<2>、<3>、<4，4>。

步骤5重复步骤3 和步骤4，直到任一倒排索引指向NULL。

继续计算模式p的支持度，当获得第1 层的下一个位置3 时，因为3 已经存在于使用字典u中，即'b'：［2，3］，所以不满足一次性条件，因此，选择下一个位置4。重复上述步骤，可以得到模式p在s1中的第2 次出现<4>、<5>、<7，7>，即<4，5，7>。同时，更新使 用字典为u=｛'a'：［3，7］，'b'：［2，3，4，5］，'d'：［4，7］｝。当寻找下一个出现时，第1 层的倒排索引指向NULL，算法结束。

SupII 算法的伪代码如算法1 所示。

算法1SupII 算法

3.3 候选模式生成

传统的序列模式挖掘方法通常采用I-Connection和S-Connection 来生成候选模式，这种方法的本质是枚举策略，虽然可以避免遗漏有希望的候选模式，但同时也会产生大量冗余的模式而极大地增加运行时间。为了解决这个问题，本文采用模式连接策略来生成候选模式。

定义9（前缀和后缀模式，子模式和超模式）如果一个长度为m的模式p=e1，e2，…，em，那么模式r=e1，e2，…，em-1和q=e2，e3，…，em分别为模式p的前缀和后缀，表示为r=prefix（p）和q=suffer（p）。此外，模式r和q被称为模式p的子模式，模式p又被称为模式r和q的超模式。

定义10（I-Join，S-Join）给 定2 个长度为m的弱间隙强模式q和r，其中，模式r表示为r=e1，e2，…，em-1，em。如果suffer（q）=prefix（r），根据em-1，em可 分为以下2 种情况：

1）em-1和em存在于同一个项集中。在这种情况下，使用I-Join 的方法生成超模式t，即添加项em到模式q的最后一个项集中，表示为t=q⊕r。

2）em-1和em存在于2 个不同项集中。在这种情况下，使用S-Join 的方法生成超模式t，即将项集（em）附加到模式q的末尾，表示为t=q⊗r。

例7给定3 个4 长度的弱间隙强模式p=（b）*（ab）*（d），q=（ab）*（de）和r=（ab）*（d）*（e），可 知，suffer（p）=prefix（q）=prefix（r）=（ab）*（d），因此，模式p和q可以通过I-Join 生成超模式t1=（b）*（ab）*（de），模式p和r可以通过S-Join 生成超模式t2=（b）*（ab）*（d）*（e）。

定义11（模式连接）用2 个长度为m的频繁模式通过I-Join 和S-Join 生成长度为m+1 的候选模式，这个方法被称为模式连接。需要注意的是，在使用I-Join 方法时，同一项集内的项要按字典顺序排序。

例8给定1 长度的频繁模式集：｛（a），（b），（d）｝，可以通过I-Join 生成超模式（ab）、（ad）和（bd），但是模式（da）不合规则，因为它没有按照字典顺序排序。

下面通过例9 来阐述模式连接策略的优越性。

例9给定2 长度的频繁模式集｛（ad），（b）*（a），（d）*（b）｝和1 长度的频繁模式集｛（a），（b），（d）｝。如果采用传统的I-Connection 和S-Connection方法生成候选模式的话，将得到12 个3 长度的候选模式。但是如果采用模式连接策略，只生成（ad）*（b）、（d）*（b）*（a）和（b）*（ad）3 个候选模式。显然，模式连接策略大幅减少了候选模式的数量。因此，模式连接策略优于I-Connection 和S-Connection 方法，能够有效缩减候选模式数量，达到提高挖掘效率的目的。

模式连接策略的伪代码如算法2 所示。

算法2PatternJoin 算法

3.4 OWP 算法

本节通过OWP 算法来挖掘序列数据库中所有频繁的一次性弱间隙强模式，具体步骤如下：

步骤1遍历序列数据库D，创建倒排索引I。

步骤2计算各项的支持度，剪枝不频繁的强项并将频繁的强项存入FP1与FPItem。

步骤3在FPm-1（m≥2）基础上，使用模式连接策略生成长度为m的候选模式Candim。

步骤4通过SupII 算法计算Candim中每个候选模式的支持度，并将频繁的模式存入FPm与FPItem。

步骤5重复步骤3 和步骤4，直到没有新的候选模式生成，算法结束。

OWP 算法的伪代码如算法3 所示。

算法3OWP 算法

OWP 算法主要有以下2 个优点：1）OWP 采用倒排索引结构，避免了对原始序列数据库的重复扫描，并且使用项的出现位置计算模式支持度，提高了搜索与计算效率；2）OWP 采用模式连接策略生成候选模式，减少了冗余候选模式的生成，其效率远远优于经典的I-Connection 和S-Connection 方法。

3.5 时空复杂度分析

3.5.1 时间复杂度

OWP 算法的时间复杂度为O（k×N/r+L×logaL），其中，k、r、N和L分别为模式最大长度、1 长度模式的数量、序列总长度和候选模式数量。

OWP 算法的时间复杂度主要由准备阶段、支持度计算和候选模式生成3 个部分构成。在准备阶段，创建倒排索引，其时间复杂度为O（N/r）；在支持度计算阶段，SupII 算法的时间复杂度为O（k×N/r）；在候选模式生成阶段，模式连接策略的时间复杂度为O（L×logaL）。因此，OWP 算法的时间复杂度为O（N/r+k×N/r+L×logaL）=O（k×N/r+L×logaL）。

3.5.2 空间复杂度

OWP 算法的空间复杂度为O（k×N/r+L），其中，k、r、N和L分别为模式最大长度、1 长度模式的数量、序列总长度和候选模式数量。

OWP 算法的空间复杂度由准备阶段创建的倒排索引、支持度计算时占用的内存空间和生成的候选模式3 个部分组成。其中，准备阶段创建的倒排索引的空间复杂度为O（N/r）；在支持度计算阶段，SupII 算法的空间复杂度为O（k×N/r）；在候选模式生成阶段的空间复杂度为O（L）。因此，OWP 算法的空间复杂度为O（N/r+k×N/r+L）=O（k×N/r+L）。

4 实验分析

4.1 实验数据集

本文采用6 个真实数据集来验证OWP 算法的运行效率，其中，D1 是项集序列数据集，D2、D3 是序列数据集，D4、D5 和D6 是氨基酸数据集，都是单项序列数据集。

实验运行环境：操作系统为64 位Windows 10，处理器为Inter®CoreTMi5-9300U，主频为2.20 GHz，内存为8 GB，开发语言为Python，开发环境为PyCharm。

表2 所示为所选用数据集。

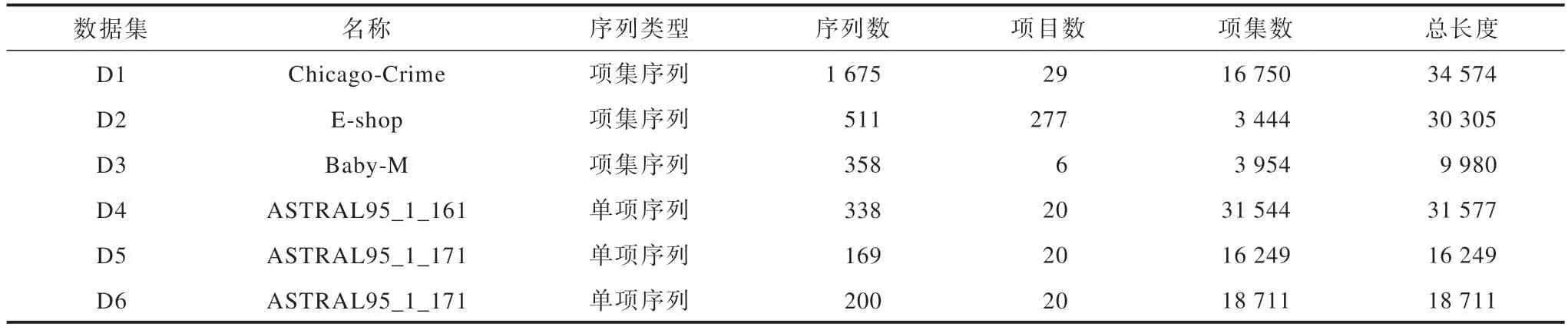
表2 实验数据集Table 2 Experimental datasets 单位：个

4.2 对比算法

本文主要采用以下对比算法：

1）OWP-p：为验证准备阶段剪枝策略的有效性，本文设计了OWP-p 算法，与OWP 算法相比，该算法没有使用此剪枝策略。

2）Ows-OWP：为了验证SupII 算法在计算支持度方面的优越性，采用Ows-OWP 算法作为对比，该算法采用文献［27］提出的one-way scan 算法计算模式的支持度。

3）OWP-e：为了验证模式连接策略的有效性，使用OWP-e 算法作为对比算法，该算法在候选模式生成时采用以广度优先为基础的枚举法。

4.3 挖掘效果

本文采 用3 个对比算法OWP-p、Ows-OWP 和OWP-e 在D1～D6 这6 个数据集上进行实验，设置不同数据集上的minsup 分别为450、500、600、35、24 和20。其中，D1～D3 为项集序列数据集，随机设置其10%的项为弱项，D4～D6 为氨基酸序列，设置非必要氨基酸为弱项，即弱项集合为ω=｛A，D，E，U，O，X｝。图2、图3 和表3 分别为运行时间、内存消耗以及候选模式数量的对比结果。

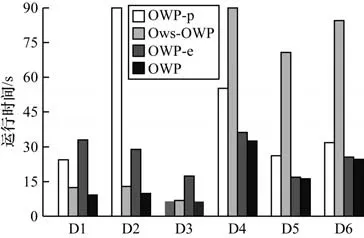
图2 D1～D6 运行时间对比Fig.2 Comparison of D1～D6 running time

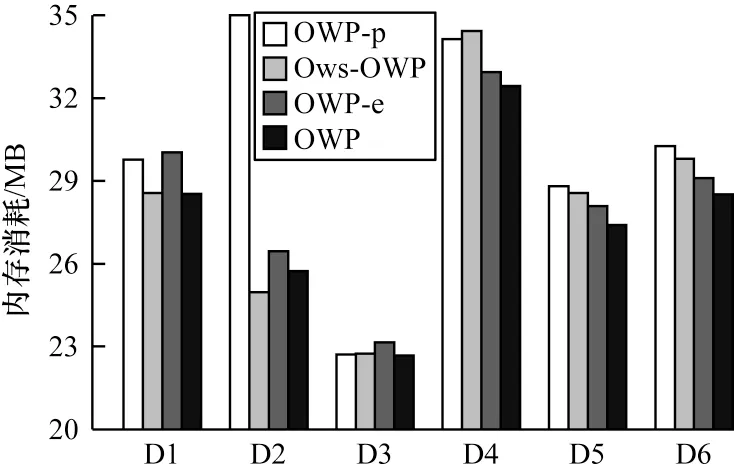
图3 D1～D6 内存消耗对比Fig.3 Comparison of D1～ D6 memory consumption

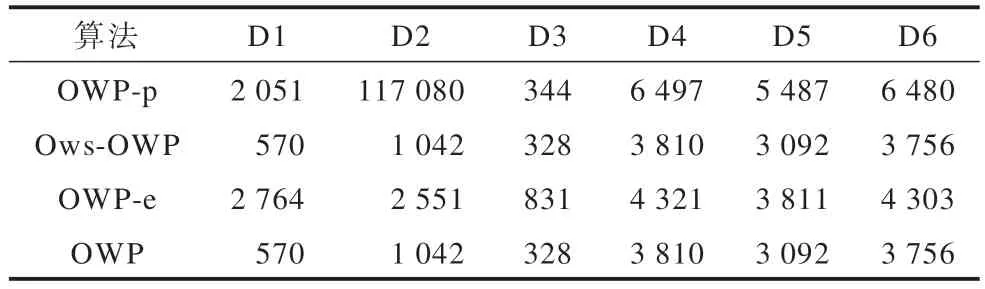
表3 生成的候选模式数量Table 3 The number of candidate patterns generated 单位：个

根据上述实验结果，可以得出如下结论：

1）剪枝策略可以有效提高算法效率。OWP 的效率优于OWP-p。以D1 为例，观察图2、图3 和表3可知，OWP 和OWP-p 的运行时间分别是9.20 s 和24.41 s，内存消耗分别是28.53 MB 和29.76 MB，生成的候选模式数量分别为570 个和2 051 个。运行时间增长了24.41/9.20=2.653 倍，内存消耗减少了3.51%。类似情况出现在每个数据集上，主要原因是：对非频繁强项和所有弱项进行剪枝，即缩减了FP1的大小，在生成2 长度的候选模式时，可以大大地减少在I-Join 和S-Join 过程中产生的冗余模式，同时减少了计算冗余候选模式支持度而造成的时间和空间的浪费。因此，剪枝策略可以有效提高算法的运行效率。

2）无论在项集序列数据集上还是在单项序列数据集上，OWP 的表现优于Ows-OWP。在运行时间方面，OWP 的运行时间少于Ows-OWP。以D1 为例，由表3 可知，在OWP 和Ows-OWP 都生成570 个候选模式的情况下，通过图2 可以看出它们的运行时间分别为9.20 s 和12.40 s。类似的情况也出现在其他数据集上，出现这种情况的主要原因是：SupII算法采用倒排索引结构，利用项目出现的位置索引计算模式支持度，避免了重复扫描数据库造成的时间浪费，因此运行时间大大缩短。在内存消耗方面，观察图3 可知，除了在D2 中，OWP 比Ows-OWP 的内存消耗高，分别是25.73 MB 和24.96 MB，在其他数据集中OWP 算法的内存消耗都低于Ows-OWP 算法，造成这种情况的原因是：由于SupII 算法需要提前申请额外空间来构建倒排索引，这产生了一定的内存消耗。当数据集的项数较多时，如D2 有277 个，这就使得OWP 占用的空间略微增加。根据表2 可知，其他数据集的项目数较少，所以OWP 用于创建倒排索引产生的空间消耗较低。因此，在内存消耗方面，OWP 算法在项数较多的数据集上内存消耗略高，在项数较少的数据集上内存消耗略低。根据图2、图3 可知，以D1 为例，OWP 比Ows-OWP的运行时间增长了12.40/9.20=1.348 倍，内存消耗减少了0.07%。综上所述，OWP 算法优于Ows-OWP算法。

3）模式连接策略可以有效减少候选模式的数量。无论在项集序列数据集上还是在单项序列数据集上，OWP-e 的运行时间、内存消耗和候选模式的生成数量均大于OWP。以D1 为例，由图2、图3 和表3可知，OWP 和OWP-e 的运行时间分别是9.20 s 和33.05 s，内存消耗分别是28.53 MB 和30.02 MB，生成的候选模式数量分别是570 个和2 764 个，运行时间增长了33.05/9.20=3.592 倍，内存消耗减少了5%。这种情况也普遍出现在其他数据集上，出现这一情况的原因如下：OWP 采用模式连接策略，可以减少冗余候选模式的生成数量，也减少了用于计算它们支持度的时间和内存消耗。因此，OWP 算法优于OWP-e 算法。

综上所述，OWP 算法可以比其他对比算法更高效地挖掘一次性弱间隙强模式。

4.4 可扩展性

为了验证OWP 算法的可扩展性，分别选取3 个对比算 法OWP-p、Ows-OWP 和OWP-e，在 以D1 为基础的数据集D1_1、D1_2、D1_3、D1_4、D1_5、D1_6上进行实验。这些数据集分别是D1 大小的1～6 倍。设置不同数据集上的minsup 分别为450、900、1 350、1 800、2 250 和2 700。图4、图5 分别为挖掘结果的运行时间和内存消耗对比。

图4 不同大小数据集上的运行时间对比Fig.4 Comparison of running time on different size datasets

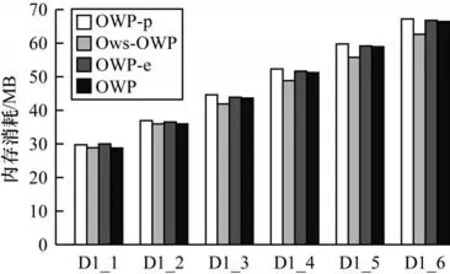
图5 在不同大小数据集上的内存消耗对比Fig.5 Comparison of memory consumption on different sizes datasets

观察图4 和图5 可以得出以下结论：

OWP 算法在运行时间和内存消耗方面都随着数据集的增大呈线性增加。比如，OWP 算法在D1_1上的运行时间为9.20 s，内存消耗为28.73 MB，在D1_6 上运行时间为34.62 s，内存消耗为66.39 MB，即运行时间增长了34.62/9.20=3.763 倍，内存消耗增加了66.39/28.73=2.310 倍。由此可见，OWP 的运行时间和内存消耗增长的倍数远低于数据集大小增长的倍数，证明OWP 具有良好的可扩展性。此外，OWP-p 的运行时间增长了130.26/24.41=5.336 倍，内存消耗 增加了67.20/29.76=2.258 倍；Ows-OWP 的 运行时间增长了51.54/12.40=4.156 倍，内存消耗增加了62.62/28.87=2.169 倍；OWP-e 的运行时间增长了163.87/33.05=4.958 倍，内存消耗增加了66.39/30.02=2.212 倍。分析可知，在运行时间上，其他3 种对比算法增加的倍数要高于OWP，但是在内存消耗上其他3 种对比算法的表现要略微优于OWP。出现这种情况的原因是：OWP 采用的剪枝策略、SupII 算法和模式连接策略有效提高了算法的运行效率，但同时OWP 由于采用SupII 算法计算支持度，当数据集变大时，创建倒排索引所占据的空间也会变大，因此比Ows-OWP 消耗了更多内存空间。然而，OWP-p 和OWP-e 生成的冗余候选模式虽然会造成一定的内存占用，但是由于数据集项数较少且不随着数据集变大而增加，因此它们内存消耗增加的倍数要略微低于OWP。

综上所述，OWP 的挖掘性能不会随着数据集的增大而降低，因此，OWP 在大数据集上也可以高效地挖掘出用户感兴趣的模式。

5 结束语

本文提出在更具通用性的项集序列数据集上挖掘一次性弱间隙强模式的OWP 算法。在准备阶段，通过扫描数据库对序列中的各项创建对应的倒排索引，并采用剪枝策略剪枝弱项和非频繁强项，精简1长度的频繁模式集合。在支持度计算方面，采用倒排索引结构，根据模式出现位置索引计算候选模式支持度，避免重复扫描数据库带来的时间消耗，从而大幅提高了运行效率。在候选模式生成方面，采用基于Apriori 属性的模式连接策略，有效减少候选模式的生成数量。在真实数据集上的实验结果验证了OWP 算法的高效性与可扩展性。下一步将对如何解决弱间隙约束条件重复判断的问题进行研究，以达到在序列、模式增长或者出现次数增加时，可以高效计算模式支持度。