分布式数据库的精简频繁模式集及其挖掘算法*
贾 泂, 刘 群, 姜 晗
(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.济宁职业技术学院 计算机工程系,山东 济宁 272000)
0 引 言
自Agrawal于1993年首次提出布尔型关联规则问题及相应的Apriori算法[1]以来,压缩庞大的频繁模式集及挖掘压缩的频繁模式集是数据挖掘领域研究的重要课题之一,其中最大频繁项集和频繁闭项集的挖掘更是最近研究的一个热点问题.现有的最大频繁项集和频繁闭项集的挖掘算法大多局限于单机环境,从单机的事务数据库中直接挖掘,一般需要维护大量侯选项集并进行超集检测,具有较高的时间和空间复杂度[2-3].挖掘分布式数据库压缩的频繁模式集算法目前尚不多见,可用的分布式系统的关联规则挖掘算法主要有PDM[4],CD[5],FDM[6],FPM[7]和FMAG[8],它们的目标是求解出存在于本地的全局大频繁项集和全局频繁项集.这些算法主要分为2类:一类是采用Apriori-like算法思想,如FDM和FPM算法在自底向上(Apriori-like算法的思想)的搜索过程中,对局部候选项集进行有效修剪,在一定程度上提高了算法的效率;另一类是采用FP-tree(frequent pattern tree)存储结构,如FMAGF通过传送条件频繁模式树或条件模式基来挖掘全局频繁项集,可以有效降低网络的通信开销,提高全局频繁项集的挖掘效率[9].但在产生频繁模式集以后,一个站点将保存本地存在的所有频繁项集及其支持数,其数据量是非常大的.无论是采用哪一种算法,都没有对其进行任何有效的精简压缩.基于此,本文提出了分布式数据库频繁模式集的精简表示及精简关联规则的挖掘算法,该算法能在分布式数据库中各局部站点的全局大项目集的基础上,迅速得出各局部站点与整个分布式数据库的频繁模式集的精简表示.
1 相关概念与性质
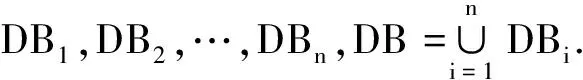
Pasquier等[11]首先提出了频繁闭项集和最大频繁项集的概念,频繁闭项集的集合表示为CFIs,最大频繁项集的集合表示为MFIs.从定义可知,基于频繁闭项集集合CFIs可以推导出所有的频繁项集及其准确的支持度,所以频繁闭项集是一个具有最小冗余的精确结果集[12].对于一个频繁项集集合,其频繁闭项集集合的最大频繁项集集合,就是该频繁项集集合的最大频繁项集集合,最大频繁项集保留了所有频繁项集的组合.在分布式数据库中:
定义1DBi上的局部频繁闭项集是指DBi上所有满足真超集的支持度均小于自身支持度的全局频繁项集.
定义2DBi上的局部最大频繁项集是指DBi上所有满足真超集的支持度均小于最小支持度的全局频繁项集.
CFIsi为在站点Si的频繁闭项集的集合,称之为局部频繁闭项集集合;GCFIs为整个数据库的频繁闭项集的集合,称之为全局频繁闭项集集合;MFIsi为在站点Si的最大频繁项集的集合,称之为局部最大频繁项集集合;GMFIs为整个数据库的最大频繁项集的集合,称之为全局最大频繁项集集合.由此可得以下性质:
性质1局部频繁闭项集一定是全局频繁闭项集;局部最大频繁项集不一定是全局最大频繁项集.
证明 若某一站点的频繁项集是局部频繁闭项集而不是全局频繁闭项集,那么必存在一真超集的支持数与其支持数相等,且必有此项目集与此真超集同时出现,故与其为局部频繁闭项集矛盾.由定义2容易证明局部最大频繁项集不一定是全局最大频繁项集.
性质2如果一个来自站点Si的局部最大频繁闭项集在别的站点不存在为其真超集的局部最大频繁项集,那么该局部最大频繁项集是全局最大频繁项集.
性质3MFIsi⊆CFIsi⊆FIsi.
若某站点的某局部最大频繁项集为全局最大频繁项集,则称该最大频繁项集是该站点全局大的,其集合为GMFIsi.在分布式数据库得到以上所有的定义和性质后,就可以用来精简分布式数据库各站点的全局大的频繁项集和整个分布式数据库的全局频繁项集,并设计在分布式数据库中压缩频繁模式集的挖掘算法,包括局部频繁闭项集与全局频繁闭项集、局部最大频繁项集、全局最大频繁项集以及各站点的全局最大频繁项集的挖掘.
2 分布式数据库全局最大频繁项集和全局频繁闭项集的挖掘算法DGMCFIs
本算法分为2个步骤:
步骤1:局部频繁闭项集CFIsi和局部最大频繁项集MFIsi的挖掘.MFIsi和CFIsi是在站点Si的频繁项集的2种精简表示.
由性质3,将算法DMFI[2]和DCFI[2]作一些改进,将其推广到分布式数据库,在各个分支数据库的全局大频繁项集上挖掘局部最大频繁项集集合MFIsi和局部频繁闭项集集合CFIsi.
首先,以I(全局频繁1-项目集)为标准对FIsi(Si上的全局频繁项目集集合)按字典顺序排序[2-3];其次,从FIsi中挖掘局部频繁闭项集,只需把FIsi按照支持度分成若干个支持度相等的集合;第三,从每个集合中挖掘最大频繁项集,所有集合的最大频繁项集的并集就组成了DBi上的局部频繁闭项集集合;最后,从局部频繁闭项集集合中挖掘局部最大频繁项集,得出DBi的局部最大频繁项集集合.这样求局部最大频繁项集比文献[2]中扫描频繁项集求解最大频繁项集的扫描量减少许多.
每个站点的局部频繁闭项集集合CFIsi是该分支数据库全局大频繁项集的一个无损压缩,一个具有最小冗余的精确结果集,也是每个站点全局大频繁项集的一个精简表示;每个站点的局部最大频繁项集MFIsi是每个分支数据库的全局大频繁项集的一个有损压缩,它保留了每个站点的全局大频繁项集的组合,但损失了这些频繁项集的支持数.由于最大频繁项集的个数远远小于频繁闭项集的数目,更远远小于频繁项集的数目,所以挖掘最大频繁项集可以有效压缩问题解的规模,对于用户迅速发现和理解稠密集中的长频繁模式具有重要的意义.因此,利用其来精简分布式数据库的频繁模式集是一种快速简洁而有效的方法.
步骤2:全局最大频繁项集GMFIs、全局频繁闭项集GCFIs和各分支站点的全局最大频繁项集GMFIsi的挖掘.GMFIs和GCFIs是整个分布式数据库的2种精简表示,GMFIsi是Si的全局最大频繁项集.
步骤2是在步骤1的基础上进行的.由性质1及性质2可得:从各分支数据库的局部频繁闭项集挖掘全局频繁闭项集,只需对各分支数据库的局部频繁闭项集求并集.挖掘全局最大频繁项集时,为每一个局部的最大频繁项集设置一个标记位,并采用分组计数技术.在此算法中,笔者采用一个hash函数,每个站点都存有此函数,以字典排序后将第1个项目相同的局部最大频繁项集散列到同一站点,组成一组并用MFIsj表示.该站点作为这些局部最大频繁项集的计数站点.例如,可以采用某一hash函数,假设有n个站点,字典排序后以Im∈I开头的所有局部最大频繁项集都散列到站点Sm mod n并设为Si,此时在Si聚集了所有以Im开头的、来自不同站点的局部最大频繁项集的一个集合MFIsj,将散列到同一站点的不同的组分开计算,再求每组MFIsj中的最大频繁项集,即可得到以Im开头的这一组局部最大频繁项集组中的最大频繁项集GMFIsj,同时站点Si把在本地的最大频繁项集中的元素按hash函数计算后得到的地址发送到相应的站点.假设I共有q个元素,则MFIsj={MFI|MFI∈MFIsi,MFI以Im开头}表示来自不同站点的字典排序后以某一特定项目Im开头的局部最大频繁项集的集合,j(=1,2,3,…,q)表示Im在I中的次序,GMFIsj={MFI|MFI∈MFIsj,MFI在MFIsj是最大频繁项集}.
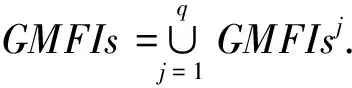

此时,各个站点就可以得到在本站点的所有全局最大频繁项集.对各个站点的全局最大频繁项集求并集,也可得到所有的全局最大频繁项集.
3 算法描述
基于频繁项集的分布式数据库精简关联规则挖掘算法(设本地为Si,每个站点同时执行)如下:
输入:全局频繁1-项集的集合I,DBi中的全局大频繁项集的集合FIsi(i=1,2,3,…,n);
输出:各个站点的局部频繁闭项集CFIsi和局部最大频繁项集MFIsi,全局频繁闭项集集合GCFIs,全局最大频繁项集集合GMFIs,在各个站点的全局最大频繁项集集合GMFIsi.
1)DCFI(I,FIsi);//returnCFIsi;
2)DMFI(I,CFIsi);//returnMFIsi;
3)broadcastCFIsi;//向其他站点广播;

5)对MFIsi按I进行字典排序;//可以利用1)排序的结果,排序后仍用MFIsi表示;
6)为MFIsi中每个元素分配一个标记位St;
7)Sm mod n=hash(Im);//把MFIsi中的元素按项目集的第1项散列到某一站点;
8)Send(MFI∈MFIsi);//按hash散列的地址,把每个MFI发送到相应的站点;
9)receive(MFI∈MFIsj),j=1,2,3,…,q;//每个站点可能有多个组,按j编组;
10)GMFIs=φ;
11)for eachMFIsjdo begin
GMFIsj=DMFI(I,MFIsj);
end
12)broadcastGMFIsj;//广播在本站点求出的全局最大频繁项集;
13)receiveGMFIsj;//接受发自其他站点的全局最大频繁项集

15)For eachMFI∈MFIsiifMFI∈GMFIs
{相应位标记为MFI.St=1;}
else
{相应位标记MFI.St=0;}//超集检测与标记全局最大频繁项集;
16)GMFIsi={MFI|MFI∈MFIsi,i=1,2,…,n,MFI.St=1};//存在于站点Si的全局最大频繁项集;

例1设某一分布式数据库有3个站点S1,S2,S3,其分支数据库分别为DB1,DB2,DB3(如图1所示),最小支持度域值为22%,经过基于分布式系统关联规则挖掘以后,按支持度降序排列的频繁1-项集I={I2,7;I1,6;I3,6;I4,2;I5,2},频繁项集的集合FIs={I1,6;I2,7;I3,6;I4,2;I5,2;I1I2,4;I1I3,4;I1I5,2;I2I3,4;I2I4,2;I2I5,2;I1I2I3,2;I1I2I5,2}.

站点S1,分支数据库DB1 站点S2,分支数据库DB2 站点S3,分支数据库DB3
各个站点的频繁项集如下:
S1站点分支数据库DB1频繁项集为{I1,6;I2,7;I3,6;I4,2;I5,2;I1I2,4;I1I5,2;I2I3,4;I2I4,2;I2I5,2;I1I2I5,2};
S2站点分支数据库DB2频繁项集为{I1,6;I2,7;I3,6;I4,2;I1I2,4;I1I3,4;I2I3,4;I2I4,2};
S3站点分支数据库DB3频繁项集为{I1,6;I2,7;I3,6;I5,2;I1I2,4;I1I3,4;I1I5,2;I2I3,4;I2I5,2;I1I2I3,2;I1I2I5,2}.
算法的执行过程如下:
1)调用DCFI,得到站点的局部频繁闭项集集合CFIsi,如S1有CFIs1={I2I4,2;I2I1I5,2;I2I1,4;I2I3,4;I1,6;I3,6;I2,7};
2)调用DMFI(I,CFIs1),得到局部最大频繁项集集合MFIsi,故有MFIs1={I2I4;I2I1I5;I2I3},同理S2,S3站点的频繁闭项集和局部最大频繁项集分别为:
CFIs2={I2I4,2;I1I2,4;I1I3,4;I2I3,4;I1,6;I3,6;I2,7},
CFIs3={I2I1I3,2;I2I1I5,2;I2I1,4;I2I3,4;I1I3,4;I1,6;I3,6;I2,7},
MFIs2={I2I4;I1I2;I1I3;I2I3},MFIs3={I2I1I3;I2I1I5};
3)broadcastCFIsi;//向其他站点广播
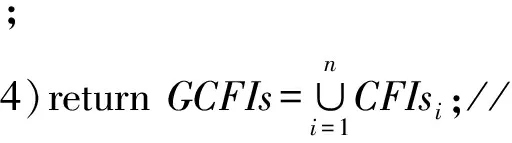
5)对本站点的局部最大频繁项集集合进行字典排序,排序后仍记为MFIsi,故MFIs1={I2I1I5;I2I3;I2I4},同理MFIs2={I2I1;I2I3;I2I4;I1I3},MFIs3={I2I1I3;I2I1I5};
6)为每一个局部最大频繁项集分配一个标记位St;
7)用hash函数对本站点的局部最大频繁项集按项目集的第1个项目散列到相应站点,第1项相同的局部最大频繁项集就被散列到同一个站点的同一组中,并用MFIsj表示,如在S1站点上MFIs1中的元素的第1项都是I2,故把它们全都发送到S2 mod 3=S2中,并被放在同一组MFIsj;
8)发送完后接受从别的站点发送过来的局部最大频繁项集,故站点S1有MFIs2={I1I3},同理在站点S2有MFIs1={I2I1I5;I2I3;I2I4;I2I1;I2I1I3},在站点S3上MFIsj=φ;
9)接收从别的站点发来的局部最大频繁项集;
10)对每个MFIsj调用GMFIsj=DMFI(I,MFIsj),故有
GMFIs1={I2I1I3;I2I1I5;I2I4},GMFIs2={I1I3},GMFIs3=φ;
11)broadcastGMFIsj;//广播本站点求出的全局最大频繁项集;
12)receiveGMFIsj;//接受发自其他站点的全局最大频繁项集;

14)forMFI∈MFIsiifMFI∈GMFIs
{相应位标记为MFI.St=1;}
else
{相应位标记为MFI.St=0;};
15)GMFIsi={MFI|MFI∈MFIsi,i=1,2,…,n,MFI.St=1};//生成存在于站点Si的全局最大频繁项集
4 算法分析
在算法DGMCFIs中,首先,基于各个站点的全局大频繁项集求出了局部频繁闭项集和局部最大频繁项集,其中先求局部频繁闭项集,再在局部闭项集中求局部最大频繁项集.显然,这样求局部最大频繁项集比文献[2]中扫描频繁项集求解最大频繁项集的扫描量大大减少.其次,在求全局最大频繁项集和存在于局部的全局最大频繁项集时,继续利用前面字典排序的结果,采用分组计数技术,将局部最大频繁项集发送到特定的站点.在此,只需将局部最大频繁项集发送到特定的站点,而不是在各个站点上求局部最大频繁项集的并集.这是因为,如果此时简单地求并集,超集检测会将每个站点的局部最大频繁项集发送到其他的每个站点,其通信量将会是巨大的,为nN(N为MFI∈MFIsi的总数).分组后先求出每组中的最大频繁项集,再求每组中最大频繁项集的并集,将大大减少网络间的通信量.第三,在得到全局最大频繁项集后,各个站点自己进行超集检测,这样就可以获得全局最大频繁项集,其通信量为(N+nM)(M为MFI∈GMFIsj的总数).采用堆排序方法的复杂度为O(nlog2n),整个算法在各个站点都能并行执行.实际上,整个算法只进行了1次字典排序,存在于各站点的全局频繁项集、局部频繁闭项集、发送到本地的局部最大频繁项集、局部最大频繁项集与最大频繁项集各扫描了1次.
5 结 语
将频繁闭项集与最大频繁项集的概念推广到分布式数据库系统中,在所需的空间与通信量尽可能少的前提下,提出了在分布式环境中全局范围内精简的频繁模式集挖掘算法,算法有效地压缩了频繁模式集.面对分布式数据库系统海量的局部与全局的频繁模式集,此种关联规则的精简表示与求解算法具有一定的现实意义.
[1]Han Jiawei,Micheline K.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2001:149-175.
[2]姜晗,贾泂.基于频繁项集挖掘最大频繁项集和频繁闭项集[J].计算机工程与应用,2008,44(28):146-148.
[3]姜晗,贾泂.基于标记域FP-Tree快速挖掘最大频繁项集[J].计算机研究与发展,2007,44(增):334-338.
[4]Park J S,Chen M S,Yu P S.Efficient parallel data mining for association rules[M]//PIssinou N K,Park E K.Proceedings of 4th International Conference on Information and Knowledge Management.New York:ACM Press,1995:31-36.
[5]Agrawal R,Shafer J.Parallel mining of association rules[J].IEEE Trans on Knowledge and Data Engineering,1996,8(6):962-969.
[6]Cheung D W,Han Jiawei,Fu A W,et al.A fast distributed algorithm for mining association rules[M]// Ng V T.Proceedings of 4th International Conference on Parallel and Distributed Information Systems.Florida:Harlequin Books Press,1996:31-44.
[7]Cheung D W,Lee S D,Xiao Yongqiao.Effect of data skewness and workload balance in parallel data mining[J].IEEE Trans on Knowledge and Data Engineering,2002,14(3):498-514.
[8]杨明,孙志挥,吉根林.快速挖掘全局频繁项目集[J].计算机研究与发展,2003,40(4):620-625.
[9]杨明,孙志挥,宋余庆.快速更新全局频繁项目集[J].软件学报,2004,15(8):1189-1197.
[10]史忠植.知识发现[M].北京:清华大学出版社,2005:69-78.
[11]Pasquier N,Bastide Y,Taouil R,et al.Pruning closed itemset lattices for association rules[M]//Lakhal Proceedings of BDA ’98 Conference.Tunisie:BDA Press,1998:177-196.
[12]Pasquier N,Basride Y,Taouil R,et al.Discovering frequent closed itemsets for association rules[M]//Beer C,Buneman P.Database Theory-ICDT ’99.Berlin:Springer,1999:398-416.

