不确定数据的约束频繁闭项集挖掘算法
牛浩浩,李孝忠,连春月
(天津科技大学计算机科学与信息工程学院,天津 300457)
数据挖掘是从数据中获取有价值的潜在信息,目的在于将海量的数据转换成有用的知识,并用所得知识对未来的行为进行指引.因此,通常也被称为数据库中的知识发现(knowledge discovery in databases,KDD)[1].在数据挖掘领域,关联规则挖掘是一种经典的挖掘方法,旨在寻找数据库中有意义的关联,在挖掘过程中需要找到需要的频繁项集[2].
在实际情况中,很多数据的产生都带有不确定性,导致原有的频繁项集挖掘算法无法直接应用于不确定数据中.目前,关于不确定数据库的频繁项集挖掘已有许多研究,如由确定数据挖掘算法 Apriori、FP-growth发展而来的 U-Apriori,UF-growth算法,以及基于此的一系列改进算法.然而,随着数据的大量增加,挖掘所得频繁项集有过多冗余项集,有些甚至是毫无意义的.最大频繁项集虽然在很大程度上减少了冗余项集,然而其并不包含项集支持度信息.而频繁闭项集[3]很好地解决了这个问题,频繁闭项集在不丢失所需信息的前提下,其数量远小于频繁项集,并包含了所有频繁项集的支持度信息[4].
目前,对于不确定数据库的频繁闭项集挖掘,主要是在不确定数据频繁项集挖掘的基础上,对频繁项集中的子集与其直接超集的支持度进行比较,由此得到频繁闭项集.对不确定数据的频繁项集挖掘,其关键步骤之一在于如何确定不确定数据的支持度信息.除了上述 U-Apriori,UF-growth等算法将期望概率作为项集支持度处理之外,文献[5]给出了概率分布的方法来近似项集的支持度计数,在已有成果中,将支持度近似为正态分布来进行挖掘的结果准确度较高[6].本文在挖掘过程中也将采取此基于正态分布的方法.
然而,目前数据挖掘方法的环境过于理想,未考虑可能存在的一些针对性条件或者决策者决策需求的偏好.因此,本文将不确定数据的支持度近似为正态分布,在其频繁闭项集挖掘过程中加入了简洁性约束条件,分别研究了在简洁反单调约束和简洁非反单调约束下,对不确定数据库进行频繁闭项集挖掘的方法.
1 相关定义
1.1 不确定数据上的概率频繁闭项集
目前,在不确定数据库中挖掘频繁项集的方法分为两大类[7]:基于期望支持度模型的方法和基于概率频繁模型的方法.
基于期望支持度模型[8]的方法最早是由 Chui等提出的,这种方法使用期望支持度来对支持度进行近似计数,在计算某项集支持度时,把数据库中该项集在每个事务中对应的概率相加,相加的结果表示该项集的支持度的估计值.因此,基于期望支持度的频繁项集有如下定义:如果项集X是频繁项集,那么X的期望支持度 esup(X)必须大于等于用户给定的最小阀值.
基于概率频繁模型[9]的方法由Bernecker在2009年提出,该方法认为在不确定性数据库中,项集的出现是不确定的,因此其支持度也是不确定的,可以使用适当的标准参数分布近似不确定项集的概率支持度计数,即支持度的概率分布,如泊松分布[5]、正态分布[6]等.
已有不确定项集支持度的近似模型中,近似效果最好的是正态分布模型[6],其相关定义[10]如下:
定义 1 频繁概率:给定一个最小支持度阈值cminsup,项集X的频繁概率是指X的支持度大于等于cminsup的概率[11],记作 Pfreq(X).
定义 2 频繁概率项集:给定一个最小支持度cminsup∈[0,n]和置信度(概率频繁阈值)τ∈[0,1],如果项集 X的频繁概率大于概率频繁阈值,则X是一个概率频繁项集,即
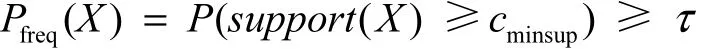
定义 3 概率支持度[12]:项集 X在置信度 τ下的概率支持度ProbSup(X,τ)定义为

其中:argmax()指使得括号内取得最大值的i值,从定义中可知,概率支持度是指满足项集X出现i次以上的概率大于等于 τ的最大的 i.也就是,在具体过程中,计算出P(support(X)≥cminsup)≥τ后,要继续计算P(support(X)≥cminsup+1)≥τ,P(support(X)≥cminsup+2)≥τ,…,直至 P(support(X)≥cminsup+n)<τ,则cminsup+n-1就是概率支持度.
定义 4 概率频繁闭项集:项集 X是概率频繁闭项集,当且仅当 Pfreq(X)≥τ,且找不到任何项集 X的超集 Y,满足 ProbSup(Y,τ)=ProbSup(X,τ)[12].
1.2 约束条件
现有的约束型频繁项集挖掘,允许用户使用一组SQL(structured query language)约束来规范其挖掘过程.根据此约束,可以挖掘满足用户需求的在事务中频繁发生的项目,此类挖掘方法可以避免挖掘无意义的频繁项集所引起的不必要计算[13].
其中,大多数用户定义的约束是简洁的,如 C1:max(X.Price)≤$25,它表示用户所感兴趣的频繁项集 X中,最贵的物品的价格不超过 25美元(即所需项集中每个项目的价格都不超过 25美元);同样的,C2:min(X.Price)≤$30表示所需项集中,价格最低的项不超过 30美元.除了购物篮项目,一套约束也可以针对其他领域的项目、事件或对象.如,C3:X.Location=Winnipeg表示用户寻求的频繁项集X的所有事件都发生在加拿大温尼伯;C4:X.Symptom={drythroat,sneezing}表示 X中的每个人都患有喉咙干燥、打喷嚏中至少一种症状.而非简洁约束,如,C5:sum(X.Price)≤$100表示挖掘所得的 X中所有项集的价格之和不超过100美元,本文对非简洁约束暂不作讨论.
除了约束是否简洁这一特性之外,还可以根据某些其他属性(如反单调性:约束 C是反单调的,当且仅当满足C的项集的所有子集也满足C)对约束条件进行划分.如,根据反单调性,简洁约束可以被划分为两类:简洁反单调约束(succinct anti-monotone constraints,SAM),简洁非反单调约束(succinct non-antimonotone constraints,SUC)[13].
上述所给简洁性约束例子中,C1、C3为 SAM;C2、C4为SUC.
2 约束条件下的概率频繁闭项集挖掘
2.1 概率频繁闭项集及其概率支持度
在挖掘概率频繁项集时,需要计算项集的概率支持度.假设项集 I在数据库中出现的次数为 XI,由于事务数据库足够大(事务数为n),将XI近似为连续的正态分布,则项集I的频繁概率为
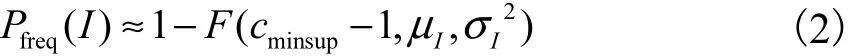
其中,F是概率密度函数的积分,即
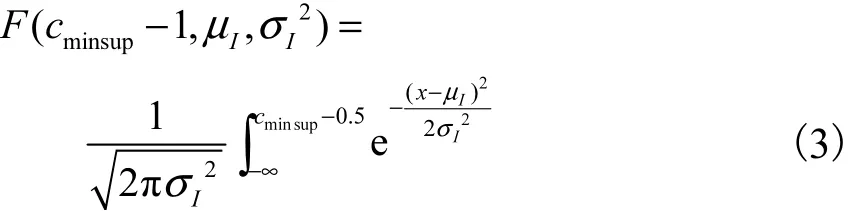
而
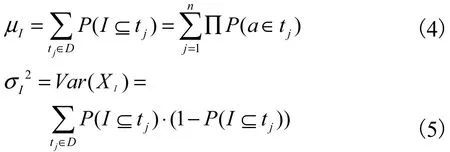
在实际情况中,可以根据数据库计算 μI和 σI2,进而求出 I的频繁概率 Pfreq(I),若 Pfreq(I)<τ,即项集 I出现 cminsup次以上的概率小于 τ,则认为项集 I是不频繁的;否则项集I为频繁项集.
根据定义 3,为了得到项集的概率支持度,在计算 P(support(X)≥cminsup)≥τ之后,需要继续计算P(support(X) ≥cminsup+1)≥ τ,…,直至P(support(X)≥cminsup+i)<τ,则 cminsup+i-1 就是其概率支持度[10].
2.2 约束条件下的概率频繁闭项集
在约束条件下,可根据约束条件将数据库中的项分为ItemM和ItemO两部分[12].其中,ItemM为强制性集合,该集合具有强制性,是因为它是约束条件下的必选项集合;ItemO表示非必选项的集合.
则对于任意约束SAM,ItemM表示满足SAM约束的项集 X,ItemO表示不满足该约束条件的项目集合,由于其反单调性,X不应包含ItemO中的项,即X应由ItemM中的项组合而成.相应地,对于任意 SUC约束,满足该约束的频繁项集应包含 ItemM中的至少一个中的项目,即目标项集应由 N1个 ItemM(N1≥1)和N2个ItemO(N2≥0)组成.
下面以实例解释数据库处理过程.表 1为不确定数据组成的交易数据库,表2为补充的商品价格信息.其中,表 1是根据用户购买习惯及浏览记录得出的购买商品及其概率,“事务”栏中的“T1,T2,T3”等表示每条成交记录,“项目”栏表示可能购买的商品及购买的概率,如 T1,{a,b,c,d,e}为其可能购买的商品,购买 a商品的概率为 0.7,购买 b商品的概率为0.8,….表2表示各商品价格,如a商品价格为10,b商品价格为20等.

表1 交易数据库Tab. 1 Transaction database
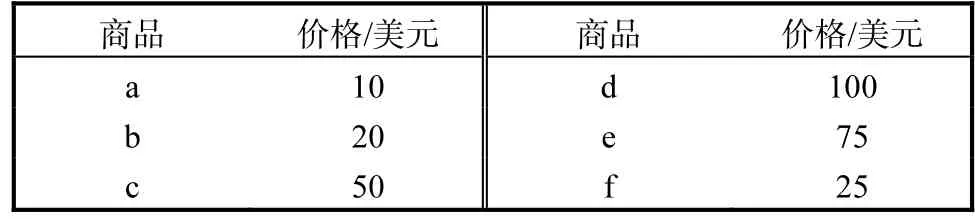
表2 商品价格表Tab. 2 Price of commodity
对于 SAM 约束 C1:max(X.Price)≤$25,根据约束的定义和要求,所挖掘的频繁项集中每项的价格应该小于等于 25美元,即所求频繁项集为小于等于25美元的项的集合.根据附加信息可得:ItemM={a,b,f}和 ItemO={c,d,e}.则对于 SAM 约束,挖掘所得频繁闭项集必须只包括ItemM中的项.
对于SUC约束C2:min(X.Price)≤$30,可以得到:ItemM={a,b}和 ItemO={c,d,e,f}.则所需约束频繁闭项集必须包含至少一个 ItemM中的项,也可能还包含有一些额外的ItemM或ItemO中的项.
3 约束频繁闭项集挖掘过程
数据被分为 ItemM和 ItemO之后,对于 SAM 约束,挖掘所得项集不包含 ItemO中的项,则可删除原数据库中ItemO包含的项;对于SUC约束,则可根据ItemM和 ItemO将原数据库分成两个子数据库后进行挖掘.
3.1 SAM约束下频繁闭项集挖掘
对于 SAM 约束 C1:max(X.Price)≤$25,可以得到 ItemM={a,b,f}和 ItemO={c,d,e}.根据约束的定义和要求,对数据库进行修剪处理.处理之后的结果见表3.

表3 SAM约束下的必选数据库Tab. 3 Mandatory database of SAM
对修剪后的数据库进行概率频繁闭项集挖掘.首先进行 1-项集挖掘,在进行挖掘之前,先对数据库进行简单的剪枝.由于任何一个非频繁项集的超集是非频繁的,所以对于 1-项集,暂时不考虑项集的概率,只计算其出现的次数,根据设定的 cminsup,若其出现次数小于 cminsup,则该项集一定不频繁,该项集的超集也是非频繁的,因此对项集进行剪枝,以减少不必要的计算.
剪枝之后,对表 3中剩余的 1-项集分别进行频繁判断:根据式(2)—式(5)可以计算数据库中各项集的频繁概率,若项集 I的频繁概率大于设定的阈值,则为 1-频繁项集,反之由于其单调性,去掉不频繁的项.对于 1-频繁项集,为了进一步进行概率频繁闭项集判断,可以根据式(1)求得项集的概率支持度.
然后采用相同的方法判断 2-项集、3-项集等是否是频繁项集,并计算其概率支持度.以例 1为例说明具体过程.
例1在上述数据表中,假设cminsup=2,τ=0.3,判断2-项集I={a,b}和1-项集J={a}是否是频繁项集.
对于 2-项集 I,μI=1.12,σI2=0.492,8,Prfreq(I)=1-Φ((cminsup-0.5-μI)/σI)=1-Φ(0.38/)<1-Φ(0.38/)=1-Φ(0.38/0.71)<1-Φ(0.53)=1-0.701,9<τ,由于 Prfreq(I)<τ,则 I为非频繁项集,无需再进行概率支持度的计算.
而对于 1-项集 J,μJ=2.2,σJ2=0.58,Pfreq(J)=1-Φ((cminsup-0.5-μJ)/σJ)=1-Φ(-0.7/)=Φ(0.7/)>Φ(0)=0.5>τ,则 J为 1-频繁项集,再根据定义3计算可得到J的概率支持度为3.
根据以上计算可得,2-项集 I={a,b}为非频繁项集,1-项集J={a}为频繁项集,其概率支持度为3.
上述步骤中 n-项集的生成,可以采用基于宽度优先的Apriori算法及其改进算法[14]或者基于深度优先的FP-Growth算法及其改进算法[15].
如在宽度优先算法中,首先根据定义 2挖掘 1-频繁项集,并得到其概率支持度;之后将 1-频繁项集链接生成 2-项集,通过相同的计算方法确定 2-频繁项集及其概率支持度,并根据定义4将1-频繁项集X与 2-频繁项集中其对应的超集 Y进行比较,若不满足定义 4,则删去前者保留后者,若满足,则均保留;再根据 2-频繁项集链接生成 3-项集…,重复上述步骤直至挖掘结束,可以得到所有满足约束条件的概率频繁闭项集及其概率支持度.
3.2 SUC约束下频繁闭项集挖掘
对于 SUC 约束 C2:min(X.Price)≤$30,按照约束(X.Price)≤$30 和(X.Price)>$30,将数据库的项分为两部分:ItemM={a,b,f}和 ItemO={c,d,e},则所需要挖掘的频繁闭项集应该由N1个ItemM(N1≥1)和 N2个 ItemO(N2≥0)组成.因此将数据库分为两个数据库:SUC下的必选数据库(表 4)及可选数据库(表 5).

表4 SUC约束下的必选数据库Tab. 4 Mandatory database of SUC
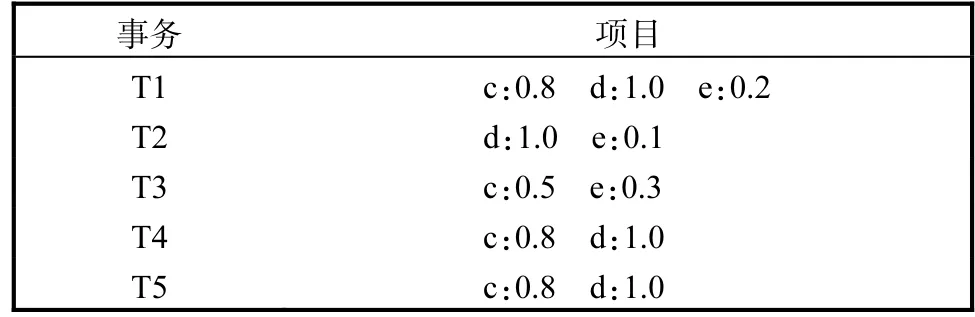
表5 SUC约束下的可选数据库Tab. 5 Optional database of SUC
首先根据剪枝条件对两个数据库分别进行剪枝,之后根据上述方法分别得到两个数据库的 1-频繁项集及其概率支持度.值得注意的是,为避免数据损失,在挖掘过程中,并不对项集X及其超集Y进行概率支持度比较,统一保留,由此可以得到两个数据库中所有的频繁项集.其中,根据约束定义可知,表 4挖掘所得频繁项集为符合约束条件的频繁项集.
下一步,由表 4数据库挖掘所得的频繁项集M(M∈ItemM)向表 5数据库挖掘所得的频繁项集N(N∈ItemO)进行扩展,过程如例2.
例 2 假设 cminsup=2,τ=0.3,从例 1可知,对于表 4数据库,ItemM中的项集 M={a}为频繁项集,对于表5数据库,计算N={c}是否为频繁项集.
对于 1-项集 N,μN=2.9,σN2=0.73,Pfreq(N)=1-Φ((cminsup-0.5-μN)/σN)>τ.
则 N为表 5数据库挖掘的 1-频繁项集,根据定义3,通过计算可得到N的概率支持度为3.
因此,以表 4数据库挖掘所得的 M={a}为基础,与表 5数据库所挖掘的频繁项集 N={c}进行结合,得到新的项集 O={a,c},接下来使用概率频繁模型判断在原数据库表 1中,项集 O是否频繁且是否与项集 M 的概率支持度相同,若其不频繁则不是目标项集,若项集O频繁则作为目标项集保留.
按照例2所述方法,以表4数据库挖掘所得的频繁项集为基础,与表5数据库挖掘所得的频繁项集进行结合,并判断是否频繁,可得到此结合方法下符合约束的频繁项集.则表 4数据库挖掘的频繁项集与结合所得的频繁项集共同构成满足SUC约束的频繁项集集合.
最后,对所得到的所有符合约束的频繁项集根据定义4进行验证,若某一项集的直接超集与其概率支持度相同,则删去该项集保留其直接超集,否则二者均保留.由此,可得到所有的目标项集.
4 结 语
本文根据概率频繁模型进行数据挖掘,将项集的支持度近似为正态分布,避免了生成不确定数据库的所有可能世界,在一定程度上减少了计算量.另外,引入了约束条件,在两种约束限制下重新对数据库进行挖掘,使得挖掘结果更满足不同的个人实际需求.然而,随着不确定数据的增多,其复杂程度也随之增加,加之现实生活中对数据库挖掘的要求也多种多样,需要有更高效更准确的不确定数据挖掘方法来解决人们对数据库的挖掘需求.接下来,可以针对SUC约束下较复杂的挖掘情况进行研究,以期获得更高的效率.并把约束思想应用于其他挖掘算法中,以满足人们对数据挖掘的不同需求.

