多率采样机制下多智能体动态事件触发二分一致性研究

范晓宇，贾新春∗，李彬，谢云飞

（1.山西大学自动化与软件学院，山西 太原 030031；2.山西大学数学科学学院，山西 太原 030006）

0 引言

近年来，多智能体系统获得了迅速的发展，它可以刻画许多自然现象［1］、移动机器人［2］、分布式电力调度［3］和传感器网络［4］。一致性是多智能体系统协同控制的核心问题，受到了学界的广泛关注［5-6］。然而，刻画不同群体之间的交互关系并不仅有合作关系，同时考虑合作和对抗交互的二分一致性更具研究意义［7-8］。关于二分一致性研究已有不少工作，其中：文献［9］针对异构线性多智能体系统设计了一种二分固定时间补偿器以实现输出编队-包围追踪控制目标；文献［10］研究了多智能体系统的预设时间二分一致性的事件触发控制；文献［11］利用一个三选项决策机制研究了多智能体系统的二分一致性以避免不受约束的控制协议设计值；文献［12］提出了一个针对网络攻击的二分追踪一致性的安全反馈控制方案。

多智能体系统的拓扑图是刻画其信息交互的有效方式。由于有向通信拓扑下2 个智能体之间的耦合权重大概率不同，因此针对于双向权值不同的符号图，一个被称为“细节平衡结构”的新的拓扑概念被提出［13］。文献［14］在此基础上研究了有限时间一致性协议。文献［15］研究了细节平衡对抗交互下多智能体系统的有限时间二分一致性。

回顾多智能体系统的一致性研究，采样控制已是不可或缺的一个分支，针对单个智能体，多数研究仅考虑了单率采样机制。为了避免单率采样中采样频率高的数据等待采样频率低的数据导致部分数据传输延迟、影响控制效果，多率采样机制被作为一种较好的解决方案被提出。多率采样机制可以针对智能体内部对应不同采样频率的传感器及时地进行数据采样传输，使得控制更具实时性。在网络化系统中，文献［16］提出了一个新颖的匹配机制来使得多率观测器和系统的多率采样信息同步，解决了带有输入时延的一般网络化系统在多率采样下的镇定问题。考虑到系统的输出采用多率采样，文献［17］提出一个分散式事件触发方法解决了网络化系统的耗散控制问题。文献［18］将多率采样机制扩展到了对多智能体系统的研究，采用动态补偿器的方法解决了异构和同构多智能体系统在多率采样下的输出和状态一致性。文献［19］在拒绝服务攻击下，基于多率采样机制实现了多智能体系统的安全一致性。

虽然多率采样机制可以充分利用采样数据，更具实时性地完成多智能体系统的控制目标，但是随着通信技术的成熟，控制动作和信号传输都高度依赖于通信网络，而在系统状态未发生较大变化时，多率采样数据并不需要高频次的传输，从而导致通信资源的浪费，甚至有堵塞网络的风险。为解决这一问题，事件触发机制作为一个有效的方案被引入多智能体系统的控制中［20-21］。文献［22］在切换拓扑下研究了多智能体系统的事件触发二分一致性。为了进一步降低事件触发的频次，一种动态事件触发机制在文献［23］中被提出。通过引入一个内部动态变量，动态事件触发可以更有效地降低通信资源的消耗［24］。文献［25］在引入内部动态变量的情况下，利用邻居智能体触发时刻广播的状态信息，设计一个基于事件的控制协议实现了一致性目标。在考虑输入饱和的情形下，文献［26］研究了基于观测器的动态事件触发二分一致性。

可以发现，在针对多智能体系统的二分一致性研究中，较少有多率采样机制下实现控制目标的成果展现，而且在多率采样机制下引入动态事件触发机制，可以充分利用采样数据，同时在一致性误差容许范围内避免文献［18］中智能体之间冗余数据传输，并可根据系统状态误差变化动态调整触发阈值。基于上述分析，本文在细节平衡的拓扑结构下，研究多率采样机制下多智能体系统的动态事件触发二分一致性。首先，在多智能体系统二分一致性的研究中引入多率采样机制，构造一个缓存器解决多率采样时序的不匹配问题；其次，设计一类多率观测器便于获得系统的估计状态以实现控制目标，通过引入动态事件触发机制，大幅减少事件触发次数；最后，基于触发时刻的观测器状态信息设计分布式控制协议，实现多智能体系统的二分一致性，并排除芝诺行为。

1 预备知识和问题建模

1.1 图论

符号图G=(V,E,H)，其 中：V={v1,v2,…,vN}是节点集；E ⊆V×V 是边集；(vj,vi) ∊E 表示存在一个边从智能体j到智能体i；H=[hij] ⊆RN×N为邻接矩阵。此外，hij＞0,(vj,vi) ∊E 表示智能体j和智能体i之间是 协同合 作的关 系，而hij＜0,(vj,vi) ∊E 表 示2 个智能体之间是对抗竞争的关系。若hij=0，则说明(vj,vi) ∉E。而对于智能体i而言，其邻居智能体可通过一个集合Ni={j|vj∊V,(vj,vi) ∊E,j≠i} 来表示。一个有向符号图G 中如果存在一条路径从任意节点vi到vj，并存在另一条路径从vj到vi，则称此图是强连通图。

图G 的Laplacian 矩阵表示为：

定义1［7］如果对于图 G 存在2 个子集 V1和V2满足V1∪V2=V，同时V1∩V2=∅，则称此图为结构平衡图，并且具有以下特性：hij≥ 0,∀vi,vj∊V1(V2)和hij≤0,∀vi∊V1,vj∊V2。

定义2［13］如果存 在一些常数γi＞0,i∊{1,2,…,N} 使 得γihij=γjhji对于任意的i,j∊{1,2,…,N}均成立，则称有向符号图 G 是细节平衡图。存在一个正定对角矩阵Γ=diag{γ1,γ2,…,γN}使得LD=ΓL 为一个对称矩阵。

假设1本文所研究的有向符号图 G 是具有细节平衡结构的结构平衡强连通图。

假设2假设矩阵对(A,B)是可镇定的，矩阵对(A,C)是可观测的。

引理1［5，7］对于一个结构平衡的有向符号图G，存在一个符号矩阵S=diag{s1,s2,…,sN},si∊{1,-1}使得矩阵SHS中的所有元素均为非负的，即SHS＞0。

引理2［7，13］假设一 个有向 符号图 G 是带有 细节平衡拓扑结构的结构平衡图，则相对应的符号Laplacian 矩阵LD有一个非负向量[s1,s2,…,sN]T作为其相对于单一零特征值的特征向量，并且LD的特征值可重新排序为λ1(LD)≤λ2(LD)≤…≤λN(LD)，其中，λ1(LD)=0 。

1.2 问题建模及多率采样机制介绍

考虑一个由N个智能体组成的多智能体系统，其中第i个智能体的动力学描述如下：

其中：xi(t) ∊Rn、yi(t) ∊Rm、ui(t) ∊Rp分别表示系统的状态、输 出、控制输 入；A∊Rn×n、B∊Rn×p、C∊Rm×n分别表示系统矩阵、输入矩阵、输出矩阵。

智能体对应于不同系统特征的输出状态应由不同的传感器进行多率采样，类似于文献［16，18］所研究的多率采样机制，本文考虑多率采样机制如下：假设智能体i的系统输出的m个分量根据其所选传感器组的采样频率不同分为r组子向量，即yi(t)=并且其中，均为整数。

如图1 所示，一个智能体的不同的输出分量有其不全相同的采样频率，表示第r个传感器组的采样时刻，其中∊N 并且表示第r个传感器组的采样周期。采用一个缓存器来储存不同传感器组所采样的输出数据，并通过零阶保持机制来获得单个智能体的缓存器组合输出状态数据：

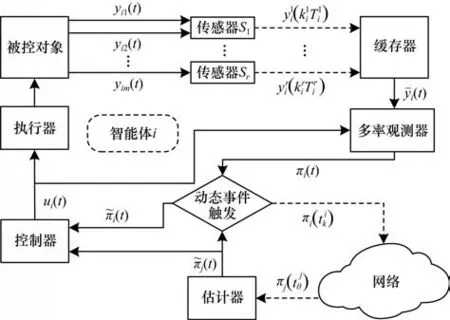
图1 多率采样机制下动态事件触发二分一致性控制框架Fig.1 The framework of dynamic event-triggered bipartite consensus control with a multi-rate sampling mechanism

通过以一个升序的方式重新排列智能体i的各传感器组的采样时刻，可以得到一个多率采样时间序列缓存器中的数据在每一个采样时刻更新，不同采样周期的传感器组在其多率采样时刻将采样数据送入缓存器，通过缓存器后，提供至多率观测器的系统采样数据为缓存器的组合输出：

由式（3）可看出，多率采样的时序不匹配问题得到解决，任意采样周期不同的传感器组数据均可转换为一连续时间下的输出yˉi(t)。

注1由式（2）及式（3）可以得出，传感器组Sr所采样的输出变量在时刻到达缓存器，而缓存器的组合输出状态yˉi(t)只更新所对应的第r个子向量，剩余的子向量均保持上一次更新的数据不变。因此，多率采样机制可以利用更为实时的采样数据，同时还避免了整个采样输出变量的同时更新。

2 控制设计及二分一致性证明

2.1 控制器及动态事件触发机制设计

如图1 所示，对于式（1）所示的多智能体系统，构造一组多率观测器以实现对于系统状态的观测并提供连续数据以便于控制器的设计，并由后续设计的动态事件触发机制确定其广播状态数据至通信网络的事件时刻。

其中：R∊Rn×m为待设计的观测器增益矩阵，其设计要求A+RC是Hurwitz 的。

针对式（1）所示的多智能体系统，提出多率采样机制下具有细节平衡对抗交互的二分一致性控制协议如下：

为了实现动态事件触发机制的设计，首先定义一个估计偏差向量判断是否将智能体i的多率观测器状态广播至通信网络的时刻由下列触发函数确定：

引理3对于给定的标量ϕi(0)、μi和βi，动态辅助参数ϕi(t)＞0,i∊{1,2,…,N}。

证明对于根据动态辅助参数ϕi(t)的动力学描述［见式（7）］可得：

因此，对于t∊[0,∞)，均有ϕi(t) ＞0 成立。

2.2 二分一致性分析

定义3若对任意的智能体i∊{1,2,…,N},j∊Ni，在任意的初始条件下，满足：

则称多智能体系统达到了二分一致性。

定理1若假设1 和假设2 成立，如果存在正定对称矩阵Q＞0 和2 个常数ρ1,ρ2＞0 满足：

则所构造的多率观测器可以有效地跟踪智能体的状态。进一步地，式（1）所示多智能体系统可以通过所设计的控制协议［见式（5）］在引入动态事件触发机制［见式（6）］的基础上实现二分一致性，且控制增益矩阵K=-BTP，而矩阵P可由下列代数黎卡提方程求解得出：

根据上述定义，可以推导得出：

基于上述分析，构造一个李雅普诺夫函数：

对其求导可得：

2.3 芝诺行为的排除

本节通过后续2 种情境的分析排除事件触发过程中芝诺行为的发生。

情境1对于智能体i而言，在范围内没有邻居智能体 满足条件触发，则由可得出：

综上所述，芝诺行为被排除。

芝诺行为意味着系统需要在有限时间内无限次地更新状态，这在实际应用中是不可能的，通过上述分析可知，连续两次事件触发时刻之间的间隔与系统控制、动态辅助参数、观测器设计及多率采样误差有关。在相关应用中，理论分析已确保芝诺行为不会发生，并可通过调节上述参数，依托于场景特征，给出两次触发之间的间隔下界以满足实际需求。

3 数值仿真

在本节中，通过一个包含3 种控制方案（多率采样动态事件触发、多率采样静态事件触发、单率采样动态事件触发）的仿真对比来验证所提控制协议的有效性。考虑一个由9 个智能体组成的多智能体系统，其满足细节平衡结构的通信网络拓扑如图2 所示（彩色效果见《计算机工程》官网HTML 版，下同）。

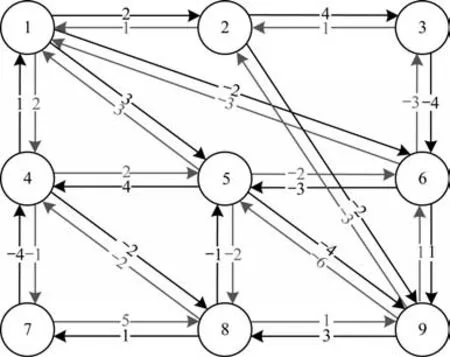
图2 带有细节平衡结构的网络拓扑Fig.2 A network topology with a detail-balanced structure

智能体的系统矩阵、输入矩阵和输出矩阵分别表示如下：

基于邻接矩阵，可得到相对应的矩阵Γ为：

Γ=diag{2,1,4,1,2,3,5,1,2}

通过求解代数黎卡提方程［见式（12）］可以得到：

控制增益矩阵K可选为：

通过极点配置法可得到观测器增益矩阵R为：

智能体初始状态为：x1(0)=col{3,-2,3},x2(0)=col{2,3,3}，x3(0)=col{1,5,2},x4(0)=col{-2,2,-3}，x5(0)=col{-3,-4,-2},x6(0)=col{-1,1,-3}，x7(0)=col{2,-1,-2},x8(0)=col{-2,4,1}，x9(0)=col{1,1,1} 。为便于对比分析，3 种控制方案下系统状态初值均一致。

取动态事件触发阈值参数的初值为静态事件触发机制下的阈值，其初始取值如下：ϕ1(0)=10，ϕ2(0)=15,ϕ3(0)=28,ϕ4(0)=13,ϕ5(0)=19,ϕ6(0)=12,ϕ7(0)=10,ϕ8(0)=20,ϕ9(0)=15。显然，在静态事件触发机制中，阈值保持不变，而在动态事件触发机制中，触发阈值是时变的。各智能体相关的控制参数见表1。

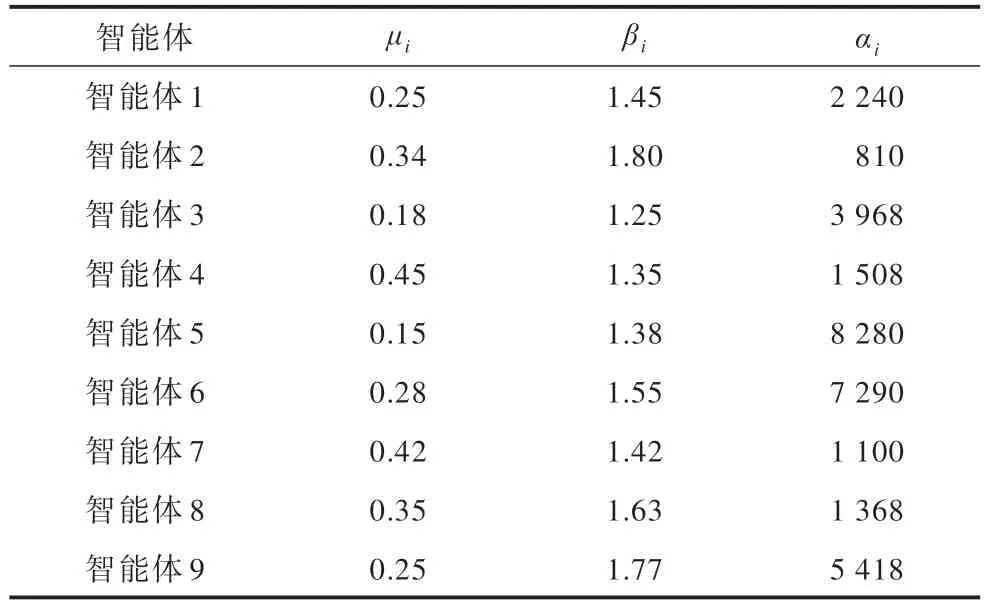
表1 控制参数Table 1 Control parameters

多率采样机制动态事件触发控制方案下多智能体系统的状态轨迹如图3 所示，其最终状态实现二分一致性。各智能体的动态事件触发时刻在图4 中展示。图5 中显示了动态辅助参数的轨迹，可看出，随着多智能体系统中智能体状态及一致性误差的变化，关于智能体是否触发的这一参数会在一致性误差较大时取相对应的较大值以降低触发次数，随着系统一致性的逐步实现，这一参数会进一步减小以保证更好的系统一致性能。

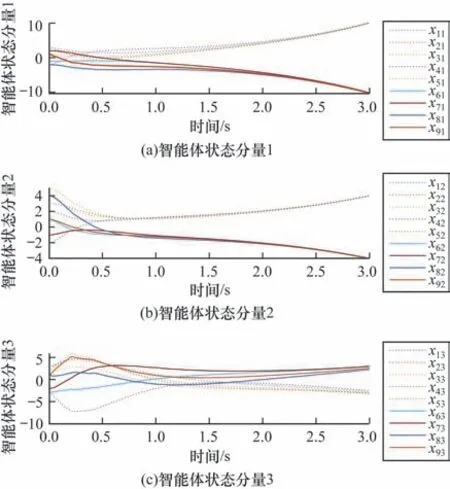
图3 多率采样动态事件触发控制下9 个智能体的状态轨迹Fig.3 The states trajectories of nine agents under a dynamic event-triggered control with a multi-rate sampling mechanism

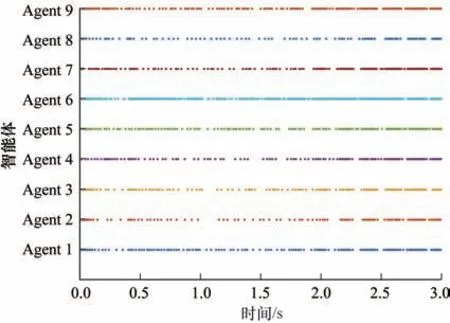
图4 多率采样机制下各智能体动态事件触发时刻Fig.4 The dynamic event-triggered instants of each agent with a multi-rate sampling mechanism

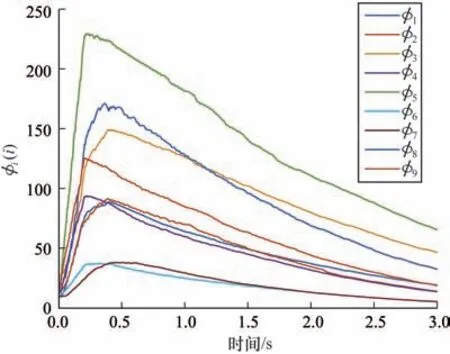
图5 多率采样机制下动态事件触发辅助参数状态轨迹Fig.5 The state trajectories of dynamic event-triggered auxiliary parameters with a multi-rate sampling mechanism

图6 给出了3 种控制方案下收敛性能对比，同时表2 给出了不同控制方案下平均事件触发次数对比。分析可得，多率采样机制可利用更为实时的系统数据，控制目标的实现更为迅速，并利用多率采样下的动态事件触发机制，可在大幅降低触发次数、减少通信负担的同时，保证更优的系统一致性能。

表2 事件触发次数对比Table 2 Comparison of event-triggered times 单位：次

图6 3 种控制方案下收敛性能对比Fig.6 Comparison of convergence performance under three control schemes

4 结束语

本文研究多率采样机制下多智能体系统的动态事件触发二分一致性。在解决多率采样时序不匹配的问题后，设计一类多率观测器便于获得系统的估计状态以构造分布式动态事件触发控制协议。利用代数黎卡提方程和李雅普诺夫稳定性理论证明系统可以在带有细节平衡结构的通信网络中实现二分一致性并排除芝诺行为。仿真对比结果证明了所提控制协议的有效性。未来的工作将考虑通信网络中存在恶意攻击的情形，研究多率采样机制下多智能体系统的动态事件触发二分一致性。