基于混合平衡优化算法的疫苗配送路径优化

陈娟，倪志伟*，李华

（1.合肥工业大学管理学院，安徽 合肥 230009；2.合肥工业大学过程优化与智能决策教育部重点实验室，安徽 合肥 230009）

0 引言

随着社会及交通工具的发展，各个地区的人流量在不断攀升，加速了传染病在人群中的传播。在各种预防措施中，注射疫苗被认为是最有效的方法［1-2］，研究疫苗的车辆路径优化问题（VRP）可以降低疫苗运输过程的成本，具有重要现实意义。

我国人口众多，在传染病爆发时期，对疫苗的需求量极大，而在爆发初期，各地疫苗储量往往难以满足全部的需求，所以要研究车辆路径优化问题，第一步必须先确定各地区的疫苗实际配送量，当疫苗供小于求时，疫苗分配常遵循公平公正的原则［3］，本文在对储量不足的疫苗进行分配时同样采取此原则。在得到各地区的疫苗实际配送量后，则要面临如何合理规划疫苗分配路径这一问题。在实际情境中，如果疫苗在规定的时间窗内未能及时到达并接种，随着到达时间的推迟，在相同的时间内，感染传染病的人数会加速增长［4］。基于此，本文将疫苗延迟到达产生的时间窗惩罚函数设置为凹函数以便更贴合实际情景。因此，在传染病爆发初期，面对疫苗储量不足的情况，在遵循公平公正原则的前提下先确定各地区的疫苗实际配送量，然后在研究车辆路径优化问题时将时间窗惩罚函数设置为凹函数将使研究更具现实意义。

疫苗储存对于温度有极高要求，因而疫苗的配送路径优化属于冷链物流车辆路径优化问题，属于VRP 的变体，国内外很多学者均对此进行了研究。在模型构建方面：ZHAO等［5］研究了包括冷链配送成本、碳排放和客户满意度的多目标模型；JI等［6］为顺应低碳经济的趋势，在研究冷链物流车辆路径优化问题时建立了3 个低碳鲁棒优化（RO）模型解决具有不确定性的问题；DENG等［7］建立了考虑货损的最小化成本模型；马成颖等［8］在考虑实时路况和客户随时需求的条件下，构建了由最小化总成本和最大化满意度组成的双目标模型；杜琛等［9］在建立模型时同时兼顾了客户满意度、油耗成本以及易腐坏货物损耗成本；王勇等［10］构建了资源共享以及温度控制下的最小化总成本的模型。在求解冷链物流车辆路径优化问题的算法方面，主要研究方向集中在用启发式算法解决问题，也有少量学者使用学习类的有关方法解决问题：LI等［11］利用了基于智能优化算法的改进粒子群优化算法结合实际案例数据求解模型；LIU等［12］提出了局部搜索效率较高的模因算法；YU等［13］采用了混合粒子群算法；马成颖等［8］通过改进的自适应大规模邻域搜索算法求解了双目标模型；任腾等［14］利用融入了禁忌搜索算法和动态概率选择的蚁群算法研究最小化总成本的模型；方文婷等［15］在求解最小化总成本的模型时，提出了A*算法和蚁群算法相结合的混合蚁群算法；雷坤等［16］为解决车辆路径问题，提出了端到端的深度强化学习框架；WU等［17］设计了一个基于自注意力的深度架构求解带容量约束的车辆路径优化模型；LI等［18］利用了一种集成异构注意机制的新型神经网络以减少车辆的总运行时间。上述研究所建立的路径优化模型多是针对生鲜冷链物流，并且求解模型的算法存在难以跳出局部最优、运行若干次后所求的最优解的值波动较大等问题。为了拓宽冷链物流的研究视角和改进算法缺陷，本文提出使用混合平衡优化算法求解疫苗冷链物流路径优化模型。

本文在遵循公平公正的原则下确定各地疫苗供小于求时的实际配送量，构建惩罚函数为凹函数以及包含碳排放成本的总成本最小化的模型。在平衡优化器中加入模拟退火算法，并且引入可变参数确定这两种算法进行粒子更新的概率，从而构建一个新的算法进行模型的求解。最后，通过对比实验验证混合平衡优化算法在求解本文所提模型上的优势。

1 模型构建

1.1 问题描述

本文提出的冷链物流车辆路径优化问题描述如下：在传染病爆发初期，疫苗由一个配送中心向N个需求点进行配送，但配送中心的疫苗储量不足以满足全部需求点的需求，配送中心也仅拥有有限的疫苗冷藏运输车，在对各需求点进行配送时，不免出现配送延迟的情况。本文研究的目标，一是在疫苗储量不足的情况下，公平公正地为各地分配疫苗，二是求解出包括固定成本、运输成本、制冷成本、碳排放成本和惩罚成本在内的最小总成本和最优配送路径。

关于本文所研究问题的假设如下：

1）所有疫苗冷藏运输车均为一种车型，最大装载量相同且始点和终点均为配送中心。

2）疫苗在配送途中始终保持活性，呈无损耗状态。

3）车辆始终中速行驶即保持匀速，避免因为剧烈颠簸造成疫苗损耗。

4）各需求点位置和需求量已知，且没有任何一个需求点的需求量大于疫苗冷藏运输车的最大装载量。

5）一个需求点仅由一辆疫苗冷藏运输车服务，但一辆疫苗冷藏运输车可服务多个需求点。

6）各需求点都要求疫苗尽快送达，故当疫苗在约定的最晚时间之前到达时无惩罚成本，只有在约定的最晚时间之后到达才会产生与时间有关的惩罚成本。

1.2 已知参数

本文中所使用的参数及含义如下所示：

N：疫苗配送中心及需求点集合，N={1,2,…,i}；

K：疫苗冷藏运输车集合，K={1,2,…,k}；

ri：第i个需求点被分配的疫苗量；

qi：第i个需求点的疫苗需求量；

f：启动一辆疫苗冷藏运输车所产生的固定成本；

s：整个配送过程中所启动的疫苗冷藏运输车的数量；

Q：疫苗冷藏运输车的最大装载量；

ti：需求点i接收到疫苗的时间；

tj：需求点j接收到疫苗的时间；

tij：疫苗冷藏运输车从需求点i行驶到需求点j所使用的时间；

r：车辆行驶单位里程所需的油耗量；

dij：疫苗需求点i和j之间的距离；

g：单位时间内制冷所需的油耗量；

e：单位油耗产生的碳排放量；

c：柴油单价；

p：碳交易所实时碳交易价格；

li：疫苗配送中心和需求点i约定的最晚到达时间。

1.3 各地疫苗实际配送量的确定

在传染病爆发初期，当疫苗储量不足时，本文为在对疫苗储量分配后，得到的各地疫苗分配量遵从公平公正的原则，引入资源满意度的概念。资源满意度为各地分配量与需求量的比值［19］，如式（1）所示，其中，Mi表示第i个疫苗需求点的满意度，ri代表第i个需求点被分配的疫苗量，qi代表第i个需求点的疫苗需求量。由极值思想可知，所有地区中最大满意度和最小满意度的差值可视为衡量公平性的标准，如式（2）所示，当差值趋近于0 时，便代表数据处理完成。

1.4 疫苗配送路径优化模型

1.4.1 决策变量分析

本文中疫苗配送中心和疫苗需求点均由i,j表示，其 中，i,j∊{0,1,…,n}，仅当i,j取0 时代表配送中心。

决策变量xijk和xik的取值如下所示：

当疫苗冷藏运输车经过i，j之间的路径，从节点i驶离后的下一个到达节点即为j，此时xijk取值为1，否则取值为0；若由车辆k向需求点i配送疫苗，那么xik为1，否则为0。

1.4.2 成本函数

关于成本函数的描述如下：

1）固定成本

在启动疫苗冷藏运输车完成配送的过程中，会产生仅与启动车辆数有关的固定成本，其中包括车辆的折旧费、保养费以及司机的工资［20］，启动一辆疫苗冷藏运输车所产生的固定成本为f，那么启动K辆所产生的固定成本C1如式（3）所示。

2）运输成本和制冷成本

疫苗冷藏运输车在配送过程中行驶和制冷产生的油耗成本分别记为C2和C3，对应运输成本和制冷成本。车辆在需求点i和j之间的运输成本可由行驶单位里程所需的油耗量r与车辆行驶距离dij的乘积得出，总的运输成本计算如式（4）所示；制冷成本为单位时间制冷所需的油耗量g与制冷总时长的乘积，如式（5）所示。

3）碳排放成本

在疫苗配送路径优化模型中，碳排放由油耗产生，且碳排放量与油耗量的正相关系数已知［21］，在文中设定为e，那么碳排放量De可由疫苗冷藏运输车所消耗的油耗量确定，如式（6）所示；在引入碳交易价格p后即可确定碳排放成本C4，如式（7）所示。

4）惩罚成本

根据文献［22］得知，如果疫苗冷藏运输车未能在约定的最晚时间到达，使得疫苗需求点延迟接种疫苗，那么传染病会快速在人群中传播，并且速度随时间不断增长，此时，惩罚函数为凹函数更符合实际。在传染病爆发初期，疫苗应尽快到达各需求点以便及时控制传染病在人群中的传播。因此：当疫苗冷藏运输车到达需求点i的时间ti在约定的最晚时间点li之前，则符合各需求地诉求，此时惩罚成本为0；当到达时间在约定的最晚时间点li之后，惩罚函数则为凹函数，如式（8）所示，惩罚成本C5如式（9）所示。

1.4.3 数学模型

本文构建的是最小化总成本的路径优化模型，总成本包括固定成本C1、运输成本C2、制冷成本C3、碳排放成本C4和惩罚成本C5，目标函数如式（10）所示。

式（10）为目标函数，由所有参加配送的疫苗冷藏运输车的运输总成本构成。式（11）～式（18）为约束条件，其中：式（11）表示任何一个配送路线的总需求量都不大于车辆的满载量；式（12）表示每个需求点都只被服务一次；式（13）表示所有车辆的始点和终点都是配送中心；式（14）和式（15）表示各需求点仅允许车辆出发到达一次；式（16）表示车辆k从客户点i到客户点j服从0-1 变量；式（17）表示车辆k服务客户点i服从0-1 变量；式（18）可保证配送过程连续。

2 算法设计

2.1 平衡优化器算法原理

平衡优化器（EO）算法［23］是一种受物理现象启发得到的新型优化算法，目的是使得容积质量动态平衡，求得最优的平衡浓度，目前成功应用于基准函数和工程问题［24］。在算法中，每一个粒子都对应着一个浓度，不同的粒子构成种群，初始种群随机产生，由前4 项最优解及其平均值构成5 个候选解，形成平衡状态池，由于粒子的更新均与候选解有关，因此该算法容易陷入局部最优进而处于停滞状态。算法的具体步骤如下：

1）初始化种群。在明确优化变量的可变化范围[Cmin，Cmax]后，在该范围内随机产生包含N个粒子的初始种群：

在式（19）中：Cmin和Cmax分别为优化变量可变范围的下界和上界；ri为随机向量，维度与种群中的粒子数量一致，向量中的每个元素均为［0，1］之间的随机数。

2）构建平衡状态池。初始化种群后，可通过计算各粒子的适应度值确定前4 项最优解，然后通过计算这4 个解的平均值确定构成平衡状态池的5 个候选解，进行粒子更新时可从中随机选取一个，每个候选解被选择的概率一致，这在一定程度上可避免粒子进行低质量的更新和缓解算法容易陷入局部最优的困境。平衡状态池的具体构成如下：

3）确定指数项系数。指数项系数与迭代次数有关，通过设置不同的参数可平衡算法全局搜索和局部寻优的能力，如式（21）所示。

其中：t可由最大迭代次数和当前迭代次数计算得出，具体如式（22）所示。

在式（22）中：a1和a2分别为控制全局搜索能力和局部寻优能力的系数，常取值为2 和1，可根据问题取不 同的值；r和γ是与ri形式相 同的向 量；IIter和IMax_Iter为当前迭代次数和算法设置的最大迭代次数。

4）确定质量生成速率。为使得算法在局部开采时得到高质量的解，EO 算法引入质量生成速率G，可由式（23）计算得出。

在上式中：Ceq是在平衡状态池中随机选出的一个候选解；C为当前待更新的解；r1和r2为［0，1］之间的随机数；PGP为生成概率。

5）进行解的更新。在经过上述4 个步骤之后，EO 算法通过下式对当前解进行更新：

其中：V常取值为1。

2.2 混合平衡优化算法

由于EO 算法的全局搜索能力较差，而模拟退火（SA）算法拥有较强的全局搜索能力，因此可在EO算法中融入SA 算法，使得改进后的EO 算法在保证解的质量的前提下，可跳出局部最优。SA 算法是依据固体退火原理提出的一种算法。在该算法中，由于固体初始温度足够高，固体中的粒子呈无序运动状态，后随着温度的降低，固体中的粒子逐渐趋于稳定，当温度降低至终止温度Tf时的固体能量即为最优解。在这个过程中的每个温度下，都要进行L次迭代，如果迭代后的能量变小，则直接接受，否则根据Metropolis 准则，以可变概率更新固体的能量。

更新概率可由下式计算得出：

其中：E1为未迭代更新前的能量；E2为迭代更新后的能量；T为当前温度，随着温度的降低，接受较高能量的概率也在逐步降低，直至最后不接受较差解。

在EO 算法中融入SA 算法后，为平衡算法的全局搜索能力和局部寻优能力，在算法中引入可变参数R：以概率R选择SA 算法更新解，进行全局搜索；以概率1-R选择EO 算法更新解，进行局部寻优。

综上，混合平衡优化算法的具体流程如下：

Step1设置相关参数。

Step2在优化变量范围内初始化种群，并将全局最优解Mnf设置为无穷大。

Step3计算种群中各粒子的适应度值。

Step4确定平衡状态池Ceq,pool，并将当前最优解mnf记为Ceq。

Step5比较全局最优解Mnf和当前最优解Ceq(1)的大小，若Ceq(1)＜Mnf，则将Ceq(1)的值赋给Mnf，否则Mnf不变。

Step6判断是否满足终止条件，是则输出最优解，流程结束，否则转至Step7。

Step7通过rand(0,1)函数生成随机数a，若a＞R，则根据EO 算法中的平衡候选解更新粒子，否则根据SA 算法更新粒子。

Step8判断种群中的粒子是否更新完毕，是则转至Step3，否则转至Step7。

以上流程对应的流程图如图1 所示。

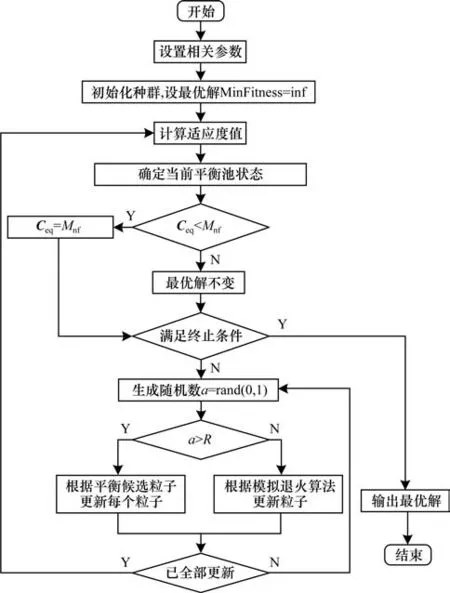
图1 混合平衡优化算法流程图Fig.1 Flowchart of hybrid equilibrium optimization algorithm

3 实例求解及分析

本文实验在Matlab 2019b 上进行编码，在Windows 10 系统下操作完成。混合平衡优化算法的初始种群设置为100，迭代总次数设置为200 次，生成概率取值为0.5，SA 算法中初始温度设置为3 000，降温系数设置为0.997。实例中疫苗需求点的坐标采用各地实际经纬度表示，两地距离通过Haversine法计算得出。

为了验证算法的性能以及其在不同规模算例下的有效性，本文在2 种规模算例下分别进行20 次实验：以安徽省内由合肥市向各市配送疫苗作为小规模算例，其中包括1 个配送中心（合肥市）、15 个疫苗需求点；以广东省内由广州市向各市配送疫苗作为大规模算例，其中包括1 个配送中心（广州市）、20 个疫苗需求点。现设置小规模算例中的配送中心（合肥市）拥有疫苗150 万剂，大规模算例中的配送中心（广州市）拥有疫苗200 万剂，除此之外，2 种算例中参数的设置均保持一致，即疫苗冷藏运输车行驶速度为60 km/h，启动一辆疫苗冷藏运输车所产生的固定成本为200 元，车辆行驶单位路程油耗费用为1.5元/km，单位时间的制冷成本为0.5元/h，柴油单价为8.18元/L，单位油耗产生的碳排放量为0.002 7 t/L，碳交易所实时碳交易价格为80 元/t，惩罚函数系数设置为150 元/h，本文用最多载重30 万剂疫苗的疫苗冷藏运输车。考虑到篇幅限制，本文仅展示小规模算例的基本信息，如表1 所示。

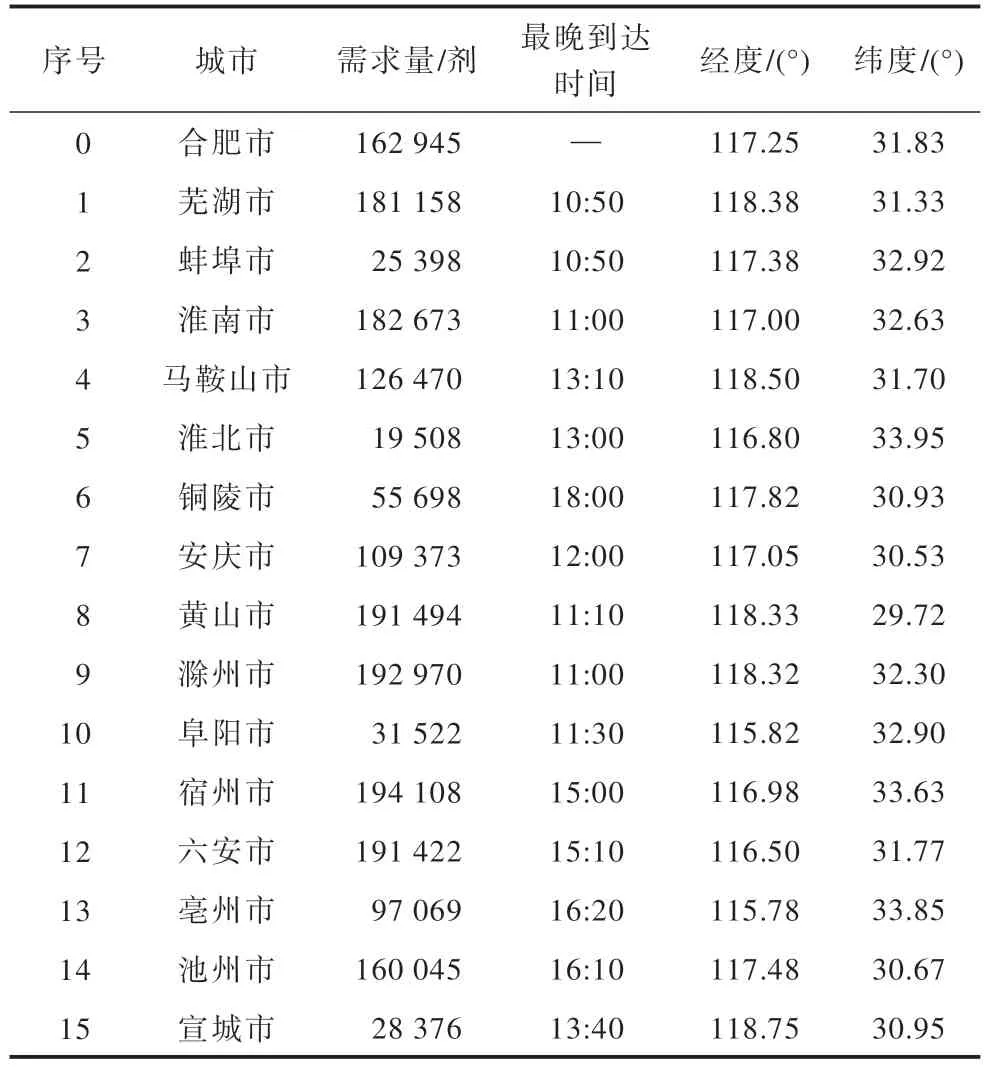
表1 小规模算例的基本信息Table 1 Basic information of small-scale examples

3.1 各地疫苗实际配送量的获取

在两种算例中各疫苗需求点的需求总和均大于配送中心的储量，此时按照公平分配原则确定的各疫苗需求点的配送量如表2 所示。由表2 可知，安徽省内各地区最大资源满意度和最小资源满意度的差值为0.000 031 231，广东省内各地区最大资源满意度和最小资源满意度的差值为0.000 033 566，差值极小，已达到公平分配。

表2 各地区实际疫苗配送量Table 2 Actual vaccine distribution by region 单位：剂

3.2 消融实验

在确定各个地区的实际疫苗配送量后，即可进行车辆路径优化实验，在此之前，为了验证本文所提的两处算法改进点的有效性，使用上述两种规模的算例分别进行20 次实验，以配送成本的最优值、均值和标准差，以及实验运行的平均时间作为衡量标准，比较EO 算法、在EO 算法中融入SA 算法得到的改进平衡优化算法和在改进平衡优化算法中加入可变参数得到的混合平衡优化算法的性能，最终的实验结果如表3 和表4 所示。

表3 配送成本的对比结果Table 3 Comparative results on delivery costs 单位：元

表4 平均运行时间的对比结果Table 4 Comparison results on average running time 单位：s

由表3 可知，以小规模算例为例，改进平衡优化算法相较于基本的EO 算法在配送成本的最优值、平均值和标准差上分别降低了62.9%、56.0%和53.2%，同时，混合平衡优化算法相较于改进平衡优化算法在配送成本的最优值、平均值和标准差上又分别降低了10.1%、29.2%和28.3%。由表4 可知，改进平衡优化算法相较于基本的EO 算法并没有因为加入了SA 算法使得算法的复杂度增加而造成实验运行时间增加的情况，混合平衡优化算法相较于改进平衡优化算法也没有出现实验运行时间增加的情况，相反，实验的运行时间还有所减少。由此可知，本文所提的两处算法改进点均能在不延长实验运行时间，甚至是在减少实验运行时间的情况下有效提升算法的性能，提高算法的寻优能力，使得算法能够稳定求出更高质量的解。

EO 算法、改进平衡优化算法和混合平衡优化算法针对小规模和大规模算例计算出的最优路径对应的迭代过程如图2 和图3 所示。

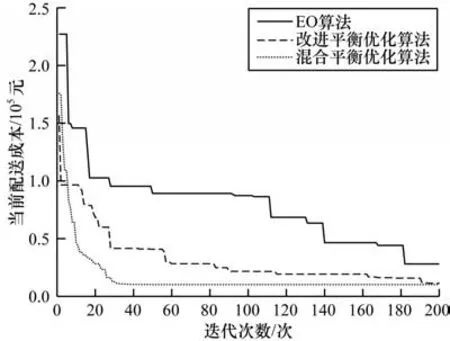
图2 迭代过程（小规模算例）Fig.2 Iterative proces（ssmall-cale example）

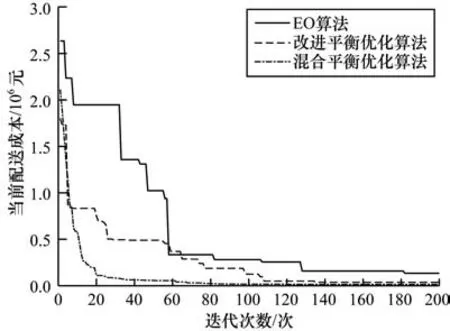
图3 迭代过程（大规模算例）Fig.3 Iterative proces（slarge-scale example）

由图2 和图3 可知，无论是针对何种规模的算例，在基础的EO 算法中依次加入两处改进点后，不仅算法的收敛速度在逐渐提高，算法跳出局部最优的能力也在逐渐提高，这更加证明了本文所提两处改进点的有效性，证明了混合平衡优化算法的有效性。

综上，采用本文所提的两处改进点改进EO 算法后得到的混合平衡优化算法具有较好的性能，并且能够更快收敛到一个较优值。

3.3 对比实验及结果分析

3.3.1 混合平衡优化算法与Cplex求解器的对比实验

将混合平衡优化算法与Cplex 求解器针对同一算例进行对比实验，算例的基本信息如表5 所示，对比实验的结果如表6 所示，表6 中使用混合平衡优化算法求得的配送成本为算法运行20 次后得到的平均配送成本。

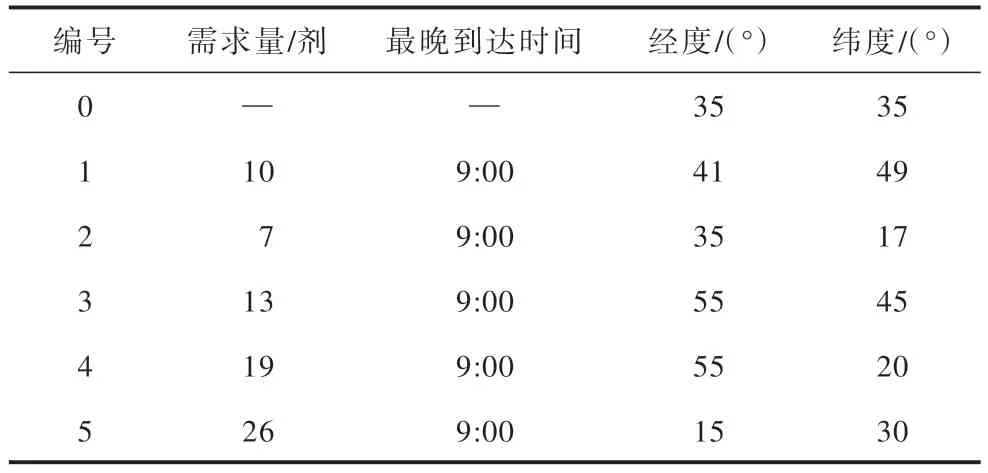
表5 需求点及各配送点的基本信息Table 5 Basic information of demand points and various delivery points

表6 针对同一算例的对比实验结果Table 6 Results of comparative experiment for one example 单位：元

由表6 可知，混合平衡优化算法所求得的配送成本相较于Cplex 求解器求得的配送成本减少了17.5%，证明了混合平衡优化算法所求解的质量高于Cplex 求解器求得的精确解的质量。

3.3.2 混合平衡优化算法与其他5种算法的对比实验

针对上文所提的两个规模的算例，将混合平衡优化算法与并行平衡优化算法［24］、知识型蚁群算法［14］、混合变邻域搜索算法［25］、改进混合粒子群算法［26］和基本的平衡优化器算法在每个算例上分别运行20 次进行对比实验，实验结果如表7 和表8 所示，表7 中数据表示最小配送成本。

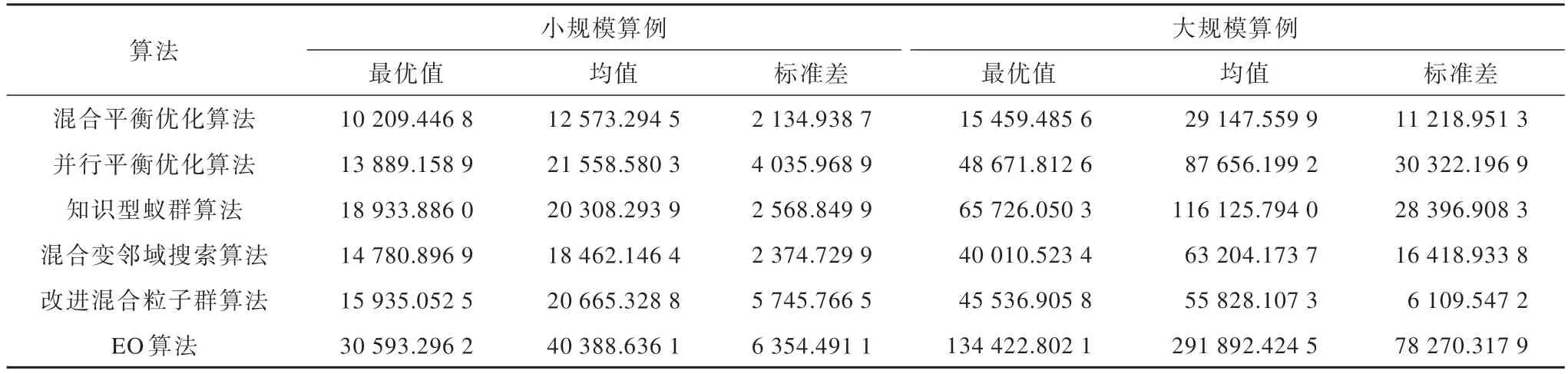
表7 针对不同规模算例的对比实验结果Table 7 Results of comparative experiment for different scale examples 单位：元

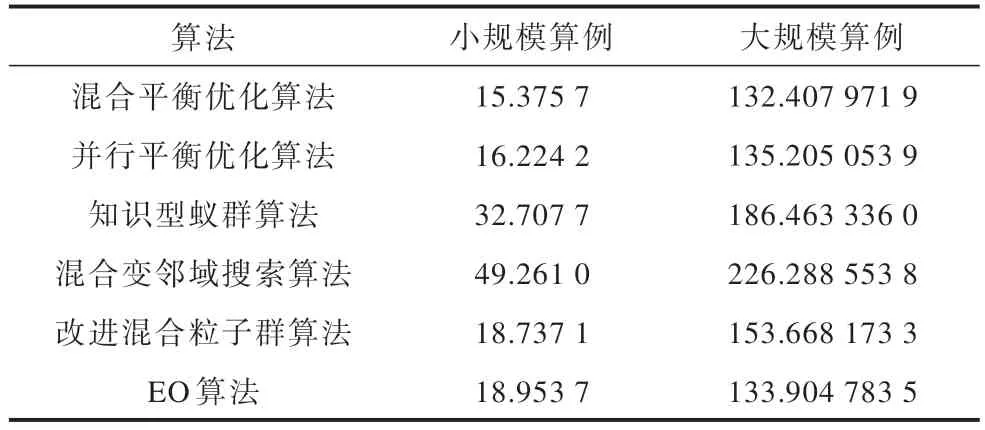
表8 不同算例规模下的平均运行时间Table 8 Average running time at different example scales 单位：s

由表7 可知，无论是针对小规模算例还是大规模算例，利用本文所提出的混合平衡优化算法求得的最小配送成本都明显小于利用其他5 种算法求得的最小配送成本。以小规模算例为例，混合平衡优化算法求得的最小配送成本分别为其他5 种算法的73.5%、53.9%、69.1%、64.1%和33.4%，混合平衡优化算法在20 次实验中求得的配送成本的均值和标准差也是6 种算法中最小的。由此可知，混合平衡优化算法不仅在不同规模的算例上具有有效性，其所求解的稳定性和质量也明显优于一些改进后的算法和基础算法。

由表8 可知，无论针对何种规模的算例，混合平衡优化算法的平均运行时间总是最小的，这表明混合平衡优化算法的计算效率更高、计算速度更快。

综上，混合平衡优化器算法不仅所求解的质量较高，其在求解时还具有较好的稳定性和较高的计算效率，因此该算法可用于求解疫苗配送车辆路径优化问题并且具有一定优势。

在本文实验中，以小规模算例和混合平衡优化算法为例，其求得的最优配送路径如图4 所示(彩色效果见《计算机工程》官网HTML 版)。

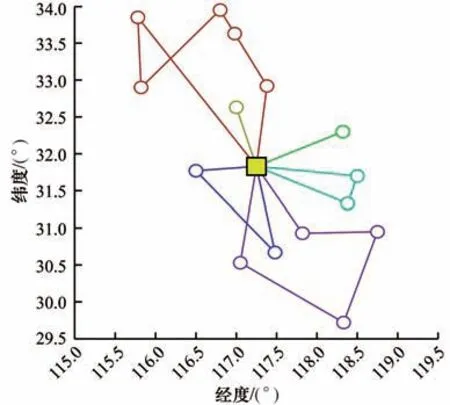
图4 最优配送路径Fig.4 Optimal delivery route

4 结束语

针对当前冷链物流车辆路径优化问题的研究多以研究生鲜配送为主。本文提出了包含碳排放成本在内的配送总成本最小化的疫苗配送路径优化模型。针对平衡优化器算法容易陷入局部最优的缺点，本文在平衡优化器算法中融入模拟退火算法，并引入起平衡作用的可变参数求解模型，得到疫苗最优配送路径。最后通过对比实验验证了混合平衡优化算法在求解本文所提模型上的优势，利用该算法求解可以较大程度地降低疫苗配送成本。下一步拟研究多配送中心和多车型情况下的疫苗配送路径优化问题，并将持续改进平衡优化器算法，提高算法的求解性能和稳定性。