等高线法:一种巧妙解决一次函数中面积问题的技巧

⦿ 湖北省武汉市陆家街中学 贾雨晴

在数学的世界中,有许多有趣而富有挑战性的问题等待我们去探索和解决.其中,构造等高平行线这一解题技巧为解决一次函数与三角形面积相关的问题提供了简洁而巧妙的方法.本文中将利用构造等高平行线的方法,通过面积相等来求解一次函数中的面积问题,并结合具体的例题和变式来展示这种方法的应用与效果.

1 灵感由来

原题如图1,直线y=kx+2经过点A(1,0),与y轴交于点B,点P(m,m-4)在直线AB上,过点B的直线l经过第一、二、四象限,且M为直线l上一点(M不与B重合),且S△OPB=S△OPM,求直线l的解析式．

图1

思路分析：将A(1,0)代入解析式y=kx+2中容易得出AB的解析式,进而将P(m,m-4)代入解析式中即可得出点P的坐标.根据S△OPB=S△OPM,可确定点M、点B所在的直线l与OP平行,因此可设直线l的解析式,再代入点B的坐标即可求解.

解：将A(1,0)代入y=kx+2,得0=k+2,解得k=-2,则AB解析式为y=-2x+2,所以点B(0,2),点P(2,-2),因此直线OP的解析式为y=-x.由S△OPB=S△OPM,可知OP∥l.设直线l的解析式为y=-x+b,代入B(0,2)得b=2,所以直线l的解析式为y=-x+2.

评析：利用平行线间的距离处处相等,结合面积相等确定动点所在的等高线,利用等高线可以解决很多类似的问题.

2 问题探究

为了更加直观说明使用等高线对求解此类问题的便捷性,以下几个变式将原题中所给的条件一般化.

2.1 将面积相等变成面积为一个定值

分析：例1与上述原题的不同之处在于,没有给出与△OPM面积相等的另一个三角形,而是给出了S△OPM=4,但只要求出△OPM等高线的解析式,再与直线l的解析式联立,即可得出所求点M的横坐标.等高线的解析式比例系数与直线OP相等,但缺少原题中点B的坐标作为辅助求出解析式,因此还需要求出一个辅助点的坐标.辅助点可以是该等高线与x轴或y轴的交点,也可以是等高线与直线x=2(与点P横坐标相同)或直线y=-2(与点P纵坐标相同)的交点.

解：根据题意,点P的坐标为(2,-2),所以直线OP:y=-x.

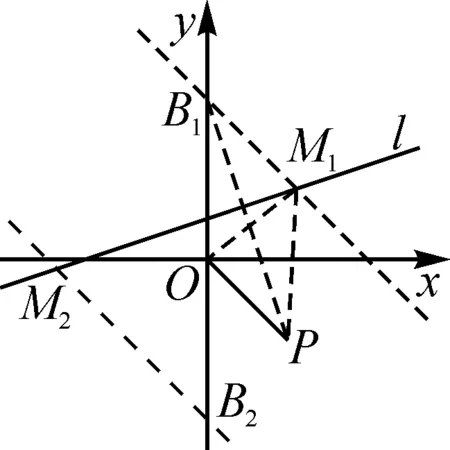
图2

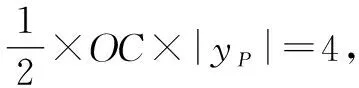
图3

图4

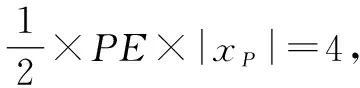
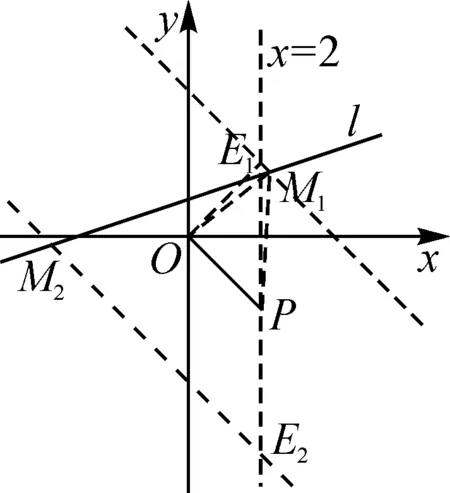
图5

评析：例1解题的灵魂在于利用点B、点C、点D、点E确定等高线的解析式.寻找这些辅助点的关键是结合已知点的位置和坐标,构造出便于计算面积的规则摆放的三角形.

这一方法适用于一次函数中与面积相关的问题.主要解题思路是:根据题意作出等高线,在等高线上构造出面积相等且规则摆放的三角形;根据面积求出辅助点的坐标,代入坐标求出等高线的解析式.规则摆放的三角形是指其中一边与坐标轴重合或平行的三角形(如例1中的△OPB,△OPC,△OPD,△OPE).

2.2 将已知点的坐标一般化

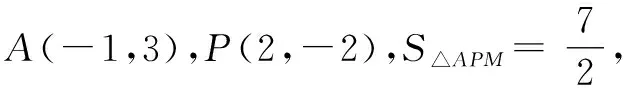
确定等高线解析式的过程中,辅助点可以是等高线与x轴或y轴的交点,也可以是与直线x=2或直线y=-2的交点,还可以是与直线x=-1或直线y=3的交点.这里仅以与y轴的交点作为辅助点进行解答说明,其余的几种情况不再一一赘述.

图6

3 思路应用

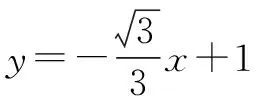
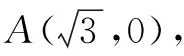
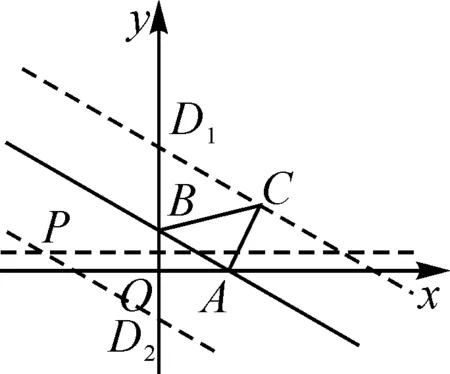
图7

利用同底等高的三角形的面积相等构造等高线是解决一次函数中面积问题的有效方法之一,其中利用直线平行得比例系数相同也是学生需掌握并熟练应用的基础知识,而灵活运用所学知识寻找辅助点更是解决此类问题的钥匙.