基于MODWPT 平方包络峭度谱的轴承声信号故障诊断方法

李方烜

（中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081）

高速动车组轴箱轴承作为走行部关键旋转部件，时常处于高转速、重载荷和多冲击的工作环境中，对其进行服役状态监测和故障诊断具有重要意义。当轴承局部发生缺陷时，无论缺陷位于轴承的外圈、内圈还是滚动体，每当轴承元件表面接触到缺陷部分时，均会引起接触面的弹性冲击，同时向外发射声信号［1-3］，滚动轴承故障轨旁声学诊断系统（简称TADS）［4］便是利用轨旁声学传感器拾取轴承声信号并随后采用一定的信号分析技术实现对滚动轴承的故障诊断。

Huang 等人最早提出了经验模态分解方法（EMD）［5］，EMD 是将原始非平稳信号分解为若干个经验模态函数（IMF）分量信号之和，已有诸多领域利用该方法进行滤波、降噪、时频分析、特征提取等，但是模态混叠、端点效应一直无法避免。随后Dragomiretskiy 等人提出了变分模态分解方法（VMD）［6-7］，该方法将非平稳信号分解为非递归、变分形式的分解模态，解决了EMD 问题，但是又引入了惩罚因子α且分解的模态个数k需要事先给定，k和α的确定取决于其他算法的支持或研究人员的经验，不同参数选择组合对分解结果影响很大。

最大重叠离散小波包变换（MODPWT）［8-9］可以有效解决上述方法在信号分解过程中出现的问题，非常适合对非平稳信号的研究。此外由ANTONI 等［10-12］提出的峭度指标对信号中的冲击成分比较灵敏，可以有效检测故障信息。因此文中将介绍利用基于MODWPT 平方包络峭度谱的轴承故障诊断方法，并通过实测轴承声信号验证该方法的可行性和有效性。

1 基本理论

1.1 MODWPT 原理

最大重叠小波包变换（MODWPT）作为一种二叉树结构滤波器组，可将原始非平稳信号在不同尺度下划分为由不同中心频率（frequency central）和带宽（band width）组成的子频带，具有很好的局部时频分辨特性，其原理如下：

对于离散时间列向量序列X｛Xt：t=0，…，N-1｝进行离散小波变换，小波滤波器hl（l=0，…，L-1）和尺度滤波器gl（l=0，…，L-1）存在的关系为式（1）、式（2）：

L为滤波器长度，假设L≤N，小波滤波器与其偶数平移长度滤波器正交，为式（3）：

定义MODWPT 的小波滤波器和尺度滤波器为式（4）、式（5）：

给出传递函数式为（6）、式（7）：

其小波滤波器满足为式（8）：

将序列X用MODWPT 法分解为分解系数Wj，n（n=0，…，2j-1，j=1，…，J）；j为分解层数；n为node，随j变化，如图1 所示。我们令W0，0≡X，根据上文给出的尺度滤波器及其传递函数(f)得到式（9）：

图1 MODWPT 分解方法

同样用小波滤波器及其传递函数(f)得到式（10）：

注意到分解系数W1，0和W1，1的长度均为N，为避免抽采样导致下一层数据点减少，对于j≥1，我们向尺度滤波器和小波滤波器分别插入2j-1-1 个0，为式（11）、式（12）：

采样该循环，进行塔式计算得到MODWPT 分解系数，为式（13）：

注：mod 表示两数取余。

1.2 平方包络峭度谱

轴承的故障信息通常由原信号中的冲击信号构成，而这些冲击信号并非总位于某一固定频带，因此需要在原信号中找到这些冲击信号才能随后对轴承进行故障诊断。平方包络峭度谱可以有效检测由MODWPT 分解得到的各个子频带中的冲击成分，从而确定故障频带，其原理如下：

对每一个MODWPT 分解系数做平方包络SE(Wj，n，t)可表示为式（14）：

峭度指标对瞬态冲击比较敏感，其定义为给定信号的四阶中心矩与二阶中心矩平方之比，对于长度为N的X（t）信号，其峭度可表示为式（15）：

式中：E·[ ]为期望计算符号，因此对于MODWPT分解系数Wj，n，t的平方包络峭度谱可表示为式（19）：

2 算法流程

文中介绍的方法首先将利用MODWPT 对非平稳信号进行分解，得到不同尺度下一系列瞬时频率和瞬时幅值分量之和，再对信号分解的各个频带做平方包络峭度计算，得到平方包络峭度谱，随后依据平方包络峭度谱中最大值确定原信号中的目标频带，接下来对目标频带进行带通滤波，最后通过包络解调［13］对轴承进行故障诊断，方法如图2 所示。接下来将采用Python 语言进行算法开发，并利用Matplotlib 进行绘图。

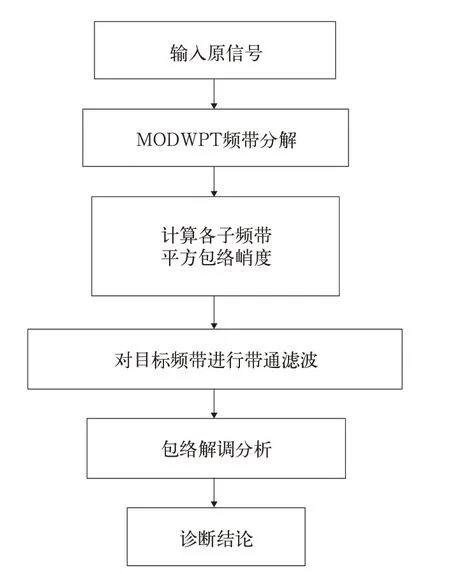
图2 轴承声学故障诊断方法

3 实测数据验证

为验证文中提出的轴承声学故障诊断方法，下面将通过2 个在动车组运用过程中产生的故障轴箱轴承样本进行故障诊断应用，由于未找到实际运用产生的轴承内圈、滚动体故障样本，因此2个样本均为外圈故障轴箱轴承。

3.1 样本一实测数据分析

3.1.1 样本一概述

样本一选取A 型动车组外圈故障轴箱轴承，分别对样本一3 次测量的轴承声学数据进行分析，相关信息见表1。

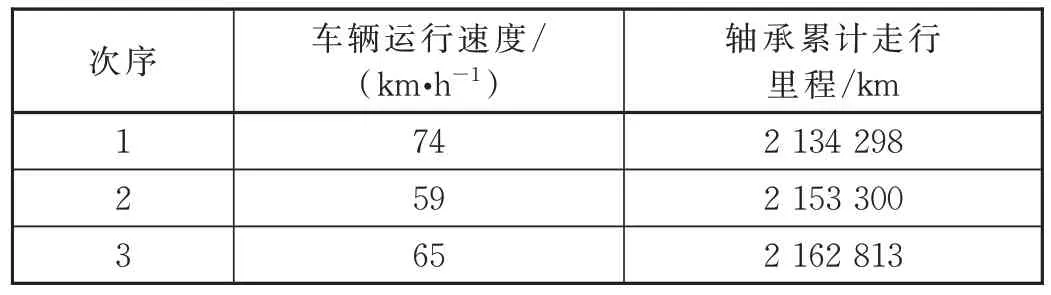
表1 样本一3 次测量信息

依据外圈故障特征频率公式可以对样本一3 次测量时的外圈故障理论特征频率进行计算，公式为式（20）：

式中：Z为滚动体数目；d为滚动体直径；D为轴承节径；fr为转频；α为滚动体接触角。

计算结果见表2。

表2 样本一理论故障特征频率 单位：Hz

3.1.2 样本一第1 次测量数据分析

蓝色信号为样本一第1 次测得的原始声信号如图3（a）所示，约0.5 s。利用文中介绍的方法计算得到原信号各子频带的平方包络峭度谱如图3（b）所示，可以观察到峭度最大值位于中心频率fc=9 544 Hz、带宽bw=707 Hz 处。接着对该目标频带进行带通滤波，得到滤波信号，h（l=9 544，h=707）如图3（a）中的红色信号所示，可以观察到滤波信号中存在一系列冲击成分，说明该频带包含轴承故障信息，此外还可以观察到目标频带中的冲击信号几乎淹没在原信号的强噪声中，这表明文中提供的方法在强噪声干扰环境下依旧可以有效定位原信号中的故障频带。最后对滤波信号进行包络解调分析，在滤波信号包络谱中可以找到67.65 Hz 的基频及其2、3 倍频，且频谱中的基频与计算得到的外圈故障理论特征频率接近如图3（c）所示，由此可验证该轴承发生了外圈故障。

图3 样本一第1 次测量数据

3.1.3 样本一第2 次测量数据分析

蓝色信号为样本一第2 次测得的原始声信号如图4（a）所示，约0.63 s。同样对原信号进行计算得到各子频带的平方包络峭度谱如图4（b）所示，可以观察到峭度最大值位于中心频率fc=10 251 Hz、带宽bw=707 Hz 处。接着对该目标频带进行带通滤波，得到滤波信号，h（l=10 251，h=707）如图4（a）中的红色信号所示，可以观察到目标频带中的冲击信号最大幅值相比第1 次已有较大增加，这是由于故障轴箱轴承此时又运行了约19 002 km，随着轴箱轴承损伤加重，包含轴箱轴承故障信息的冲击信号也愈发明显。进一步对滤波信号进行包络解调分析，在滤波信号包络谱中可以找到54.37 Hz 基频及其2、3 倍频，且基频与计算得到的外圈故障理论特征频率接近，再次验证该轴承发生了外圈故障，如图4（c）所示。此外，在包络谱中也可以发现故障特征频率的倍频成分幅值有明显增加，说明此时轴承外圈故障相较前一次更加严重。

图4 样本一第2 次测量数据

3.1.4 样本一第3 次测量数据分析

蓝色信号为样本一第3 次测得的原始声信号如图5（a）所示，约0.57 s。可以观察到原信号中已出现一系列可见的冲击成分，对原信号进行平方包络峭度谱分析如图5（b）所示，可以观察到峭度最大值位于中心频率fc=10 251 Hz、带宽bw=707 Hz处。接着对该目标频带进行带通滤波，得到滤波信 号，h（l=10 251，h=707）如 图5（a）中的红色信号所示，可以观察到目标频带中已存在十分清晰的周期性冲击信号，此时相较该轴箱轴承第1 次测量时又运行了约28 515 km，轴箱轴承损伤已严重劣化。继续对滤波信号进行包络解调分析，在滤波信号包络谱中可以很明显找到60.16 Hz 基频及其2、3、4 倍频，且基频与计算得到的外圈故障理论特征频率接近如图5（c）所示，验证该轴承发生了较严重的外圈故障。

图5 样本一第3 次测量数据

3.2 样本二实测数据分析

3.2.1 样本二概述

样本二选取B 型动车组外圈故障轴箱轴承，样本二与样本一非同型号轴承，由此尽可能保证两样本的差异性，从而验证本方法的普适性。

用相同的方法对样本二的3 段轴承声学数据进行分析，相关信息见表3。

表3 样本二3 次测量信息

同样依据公式（20）可得到样本二的故障特征频率见表4。

表4 样本二理论故障特征频率 单位：Hz

3.2.2 样本二第1 次测量数据分析

蓝色信号为样本二第1 次测得的原始声信号如图6（a）所示，约0.5 s。利用文中介绍的方法计算得到原信号各子频带的平方包络峭度谱如图6（b）所示，可以观察到峭度最大值位于中心频率fc=10 605 Hz、带宽bw=1 414 Hz 处。接着对该目标频带进行带通滤波，得到滤波信号，h（l=10 605，h=1 414）如图6（a）中的红色信号所示，可以观察到滤波信号中存在冲击成分，说明该频带包含轴承故障信息。接下来对滤波信号进行包络解调分析，在滤波信号包络谱中可以找到67.62 Hz 的基频及其2 倍频，频谱中的基频与计算得到的外圈故障理论特征频率接近，如图6（c）所示，由此可验证该轴承发生了外圈故障。

图6 样本二第1 次测量数据

3.2.3 样本二第2 次测量数据分析

蓝色信号为样本二第2 次测得的原始声信号如图7（a）所示，约0.82 s。同样对原信号进行计算得到各子频带的平方包络峭度谱如图7（b）所示，可以观察到峭度最大值位于中心频率fc=9 544 Hz、带宽bw=707 Hz 处。接着对该目标频带进行带通滤波，得到滤波信号，h（l=9 544，h=707）如 图7（a）中的红色信号所示，可以观察到目标频带中的存在较明显的一系列冲击成分。进一步对滤波信号进行包络解调分析，在滤波信号包络谱中可以找到40.86 Hz 基频及其2、3 倍频，且基频与计算得到的外圈故障理论特征频率接近，如图7（c）所示，验证该轴承发生了外圈故障。相比第1 次得到的包络谱，此时包络谱中不仅可以找到3 倍频，也可以发现倍频成分更加明显，说明故障信号特征较前一次愈发明显，这与样本二较前一次继续运行30 936 km 后损伤加重的情况符合。

图7 样本二第2 次测量数据

3.2.4 样本二第3 次测量数据分析

蓝色信号为样本二第3 次测得的原始声信号如图8（a）所示，约0.84 s。对原信号进行平方包络峭度谱分析如8（b）所示，可以观察到峭度最大值位于中心频率fc=10 251 Hz、带宽bw=707 Hz 处。接着对该目标频带进行带通滤波，得到滤波信号，h（l=10 251，h=707）如图8（a）中的红色信号所示，可以观察到目标频带中已存在十分清晰的周期性冲击信号，此时相较样本二第1 次测量时又运行了约49 870 km，轴箱轴承损伤已很严重。对滤波信号进行包络解调分析，在滤波信号包络谱中可以很明显找到39.31 Hz 基频及其2、3、4 倍频，且基频与计算得到的外圈故障理论特征频率接近，如图8（c）所示，验证该轴承发生了较严重的外圈故障。

图8 样本二第3 次测量数据

4 结论

通过实测数据验证，文中提供的方法可对故障轴承进行有效诊断，研究结果表明：

（1）基于MODWPT 的平方包络峭度法可以有效提取轴承声信号中的故障频带，且能应对一定程度的强噪声干扰。

（2）利用不同故障轴承样本进行多次算法验证，发现该方法具有不错的普适性，能够对故障轴承进行稳定识别。

（3）对比同一故障轴承样本在不同服役里程下的故障诊断结果，可以发现其能较准确地反映轴承损伤程度变化，说明该方法应用于轴承故障诊断时的有效性和准确性。