瞬变运动条件对竖直管内搅混流向环状流转变边界的影响研究

马文慧,曹夏昕,*,谢添舟

(1.黑龙江省核动力装置性能与设备重点实验室,黑龙江 哈尔滨 150001;2.中核集团核反应堆热工水力技术重点实验室,四川 成都 610041)

气液两相流的宏观运动规律及其交界面形态之间的相互作用是流体力学的主要研究内容之一[1],在气液两相流动中,相界面的变化和组合很复杂,由于气相易于压缩,相界面易于变形,因此可以构成多种不同组合的相界面并形成不同的流型。搅混流和环状流就是两种典型的流型形态。这种流型的变化会导致两相流动阻力和传热特性发生变化,在核能、热能工程等领域的系统和设备设计计算中经常需要识别不同流型形态,因此构建搅混流和环状流之间的转变准则,对于精确计算两相阻力和传热具有重要意义。几十年来国内外学者对其进行了广泛的研究,但这些研究大多在静止条件下开展[2-4]。然而在水面船舶航行中,其船体内换热系统及设备内两相流动常处于瞬变运动状态,少量研究表明,瞬变运动条件下两相汽泡行为特性与静止时存在显著的差异[5-6],可以推断不同汽泡组合形成的两相流型与静止条件下也可能会存在一定的差异。因此,有必要开展瞬变运动条件下搅混流和环状流转变准则研究。

本文针对摇摆和升潜两种典型海洋运动条件,引入运动产生的瞬变外力场,构建摇摆和升潜条件下搅混流和环状流转变准则,通过实验数据进行验证,并在模型中分析瞬变运动参数对流型转变边界的影响规律。

1 模型构建

1.1 摇摆运动的数学描述

摇摆运动是以θm为最大摇摆角、T为摇摆周期的简谐运动,其摇摆规律为:

(1)

(2)

(3)

式中:θ(t)为瞬时摇摆角位移;ω为角速度;ε为角加速度;t为时间。

1.2 升潜运动的数学描述

升潜运动是在竖直方向上呈正弦方式运动,则有:

(4)

(5)

(6)

式中:z(t)为升潜条件下瞬时位移,其正方向与重力加速度方向一致;u(t)为速度;a(t)为加速度;zm为升潜运动最大振幅;T为升潜周期。

1.3 搅混流向环状流转变准则构建

典型瞬变运动条件下环状流如图1所示。图1中:D为管道直径;JG和JL分别为气相和液相表观速度;τw为壁面剪切力;τi为气液两相交界面剪切力;δ为液膜厚度;z为流动方向。摇摆运动时,实验段绕oy轴转动,流型观测点与z轴有一个初始角度θ′,摇摆条件下真实摇摆轴r′,流动方向与竖直方向的夹角θ(t)瞬时变化;升潜运动时实验段沿z轴周期运动,气、液相受升潜引入的附加加速度a(t)影响。

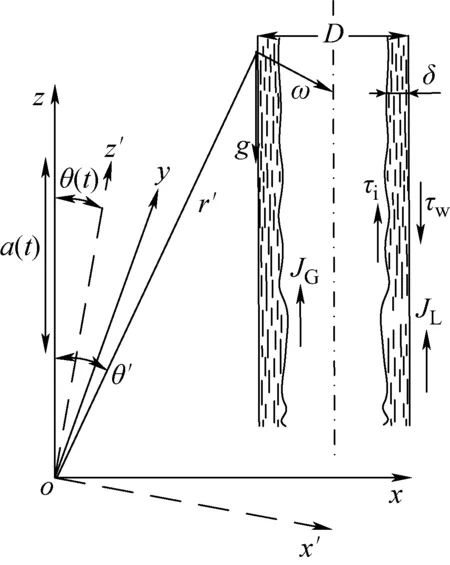
图1 典型运动条件下环状流示意图Fig.1 Schematic diagram of annular flow under typical motion condition

典型环状流时,气相在管道中心区域聚集,液相以液膜的形式环绕管壁。采用分相流模型,分别对液膜和气芯列出动量方程如下。

对于液膜,有:

(7)

对于气芯,有:

(8)

(9)

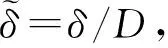
(10)

式中,壁面切应力τw为:

(11)

式中,UL为液相真实速度,其与液相表观速度JL的关系式为:

UL=JL/(1-α)

(12)

环状流时,空泡份额可通过简单的数学计算得到:

(13)

壁面与液环之间的摩擦系数fL表达式为fL=λL/4,对于光滑圆管,有:

(14)

式中,ReL=ρLULD/μL。

将式(9)～(13)代入式(14),有:

(15)

气液两相交界面剪切力系数fi采用Wallis根据实验数据拟合得到的关系式[6]:

(16)

则气液两相交界面剪切力τi与气相表观速度JG的关系式如下:

(17)

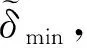
(18)

环状流时液相表面波浪从波谷向波峰移动,当液相表观速度较大时,液膜中液相轴向运动使液膜桥接导致气芯堵塞。此时环状流也会转变为搅混流,Barnea等[8]建议此时环状流的转变准则为:

(19)

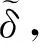
摇摆条件下,由于浮力分量及摇摆引入的附加力的影响,液相/气相所受体积力加速度[5]为:

ε(t)r′sinθ′

(20)

升潜条件下,由于升潜引入的附加力的影响,液相/气相所受体积力加速度[2]为:

g′(t)=g+a(t)

(21)

上述搅混流-环状流转变准则同样可适用于静止条件下竖直向上及倾斜流动,对于倾斜流动,g′=gcosθ;对于竖直向上流动,g′=g。

2 转变准则模型计算结果与实验数据的对比

2.1 转变准则模型计算结果与静止条件下实验数据对比

图2为本文构建的流型转变准则模型和其他模型计算结果对比,其中实验数据[9]为25.4 mm圆管内竖直和倾斜条件下实验结果。

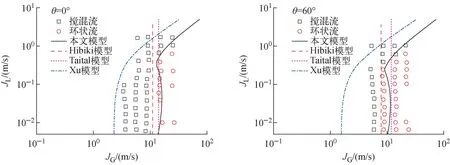
图2 计算结果与D=25.4 mm通道内实验数据的比较Fig.2 Comparison between calculation results and experimental data in D=25.4 mm channel

Hibiki等[10]认为环状流的转变是由于泰勒气泡区液膜发生流动逆转,从图2可看出,其在液相表观速度较小时符合较好,但当液相表观速度较大时由于通道内无法存在稳定泰勒汽泡,因此符合较差;Taital等[11]认为环状流时液滴受气芯的曳力刚好等于液滴的重力时发生环状流向搅混流的转变,该模型在竖直流动条件下建立,因此在倾斜条件下符合较差;Xu[12]认为空泡份额随体积份额增长发生急剧增大时出现搅混流向环状流的转变,由于其是由矩形窄缝通道内流型转变数据拟合得到的,与本文实验本体结构有显著差异,因此符合较差;本文构建的转变准则计算结果与实验数据均符合较好。

从图2可知,当气相表观速度较大时,气相在管道中心流动,液相在壁面以膜状流动,通道内为稳定的环状流,随着气相表观速度的减小,通道内环状流无法保持稳定,流型转变为搅混流。当液相表观速度较小时(JL≤0.35 m/s),转变曲线近似为竖直曲线,这是由于液相表观速度较小时,只要气相表观速度大到一定程度即可保证液膜在入口处不发生阻塞,维持环状流的稳定。而当JL>0.35 m/s时,液膜厚度增大,此时液相的轴向运动对于流型转变起主要作用,此时液相表观速度越大,维持环状流稳定所需的气相表观速度就越大。

2.2 转变准则模型计算结果与运动条件下实验数据对比

运动条件下流型转变实验在中国核动力研究设计院(NPIC)六自由度运动台上开展,两相工质为空气和水混合工质,实验通道为长1.1 m的内径24 mm圆管通道,实验水温20 ℃,压力0.2 MPa,摇摆振幅10°～30°,周期5～15 s,升潜振幅0.2～0.5 m,周期1.64～5 s,实验中流道在运动台中心位置,因此θ′=0,实验段中心处距平台1.2 m,因此有r′=1.2 m,实验装置具体布置见文献[13]。

图3为不同运动工况下搅混流向环状流转变计算结果与实验数据的对比。从图3可看出,与竖直和倾斜条件下实验结果一致,当气相表观速度较大时,通道内为稳定的环状流,随着气相表观速度的减小,流型转变为搅混流,升潜和摇摆条件转变准则模型计算结果与实验数据均符合较好。

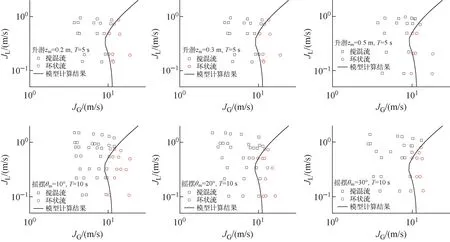
图3 不同运动条件下搅混流向环状流转变边界Fig.3 Transition boundary of churn flow to annular flow under different motion conditions

3 运动条件对搅混流向环状流转变边界的影响

图4为不同摇摆运动参数对搅混流向环状流转变边界曲线的影响。图4a中θm=40°和θm=60°和图4b中T=2.5 s曲线为模型拓展计算结果,从图中可看出,即使在模型中增大摇摆参数,搅混流向环状流转变曲线也近似不变。这是由于环状流时通道内液相很少,气相表观速度非常高且在中心聚集,即使增大运动参数,摇摆运动引入的附加力对通道中心的连续气相影响不大,因此虽然壁面液膜厚度分布会受摇摆运动影响而不均,但环状流整体结构不会破坏。

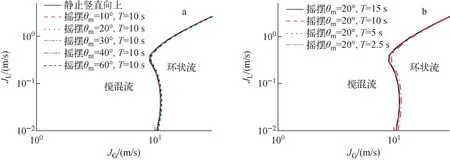
图4 摇摆运动参数对搅混流向环状流转变边界的影响Fig.4 Effect of rolling motion parameter on transition boundary of churn flow to annular flow

升潜运动参数对搅混流向环状流转变边界的影响如图5所示。图5a中zm=1 m和zm=3 m的工况为模型拓展计算结果,从图中可看出,在液相表观速度较小时,随着升潜振幅的增大和升潜周期的减小,转变曲线右移,而液相表观速度较大时,转变曲线基本不变。这是由于液相速度较小时,搅混流向环状流的转变是由于壁面液膜的下降导致入口处气芯被堵塞,此时随着升潜振幅的增大,升潜引入的附加加速度增大,液膜受竖直方向上瞬时体积力增大且周期性振荡,液膜更易下降堵塞气芯,因此需要更大的气相表观速度才能维持稳定的环状流。

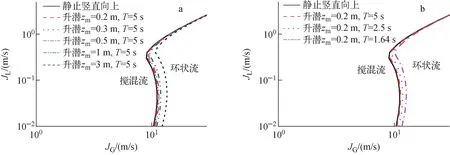
图5 升潜参数对搅混流向环状流转变边界的影响Fig.5 Effect of ascent parameter on transition boundary of churn flow to annular flow

4 结论

1) 本文构建了运动条件下搅混流-环状流转变准则模型,该预测模型同时可适用于竖直向上和倾斜流动。模型计算结果与竖直向上、倾斜、升潜和摇摆条件下实验数据进行了对比,符合较好。

2) 现有参数范围内,摇摆运动引入的附加力对通道中心的连续气相影响不大,因此虽然壁面液膜厚度分布会受摇摆运动影响而不均,但环状流结构不会破坏,搅混流-环状流转变曲线与竖直向上时基本一致。

3) 随着升潜振幅的增大和升潜周期的减小,搅混流向环状流转变界限曲线右移,这是由于升潜引入的附加加速度增大,液膜受竖直方向上瞬时体积力增大且周期性振荡,液膜更易下降堵塞气芯,因此需要更大的气相表观速度才能维持稳定的环状流。