深穿透跨尺度辐射场分析软件NECP-MCX研发及应用

吴宏春,贺清明,曹良志,黄展鹏,郑 琪,李 捷,秦 帅,黄金龙,包 彦

(西安交通大学 核科学与技术学院,陕西 西安 710049)

高精度高效率模拟核装置中的中子、光子辐射场是核装置设计研发的核心任务。辐射场的中子、光子通量密度变化幅度高达10个数量级,具有明显的深穿透特征;辐射场分析需要模拟从mm到km尺寸的中子、光子场,具有显著的跨尺度特征,对高精度高效率模拟带来了严峻的挑战。离散纵标方法和蒙特卡罗方法是主流的辐射场分析方法。离散纵标方法又称SN方法[1],具有方法简单和计算速度快的优点。然而,由于目前对屏蔽计算的精度要求越来越高,对模型精度的要求也逐渐提升,SN方法采用的直角坐标和圆柱坐标难以描述复杂几何,导致建模复杂、空间离散误差大。蒙特卡罗方法相比SN方法,在几何上可以采用CSG几何精确描述复杂几何结构,能量上采用连续能量点截面,角度上无需离散,具有较高的计算精度。但是对于深穿透问题,蒙特卡罗方法在有限的计算资源下很难获得有效计数,导致统计方差大,计算结果不可信。

针对上述问题,西安交通大学核工程计算物理(NECP)实验室自主研发了深穿透跨尺度辐射场分析蒙特卡罗软件NECP-MCX[2]。软件的研发始于2018年,并于2020年8月发布了NECP-MCX V1.5。该版本具备中子-光子耦合输运计算、临界计算、输运-燃耗耦合计算、几何建模可视化和计算结果可视化等功能。对于跨尺度深穿透问题,采用基于一致性共轭驱动重要性抽样[3](CADIS)的概率论-确定论耦合方法。该方法利用确定论进行共轭计算,产生最优权窗和源偏倚参数,从而降低蒙特卡罗前向计算的统计方差。基于HBR-2、VENUS-3和PCA等基准题对NECP-MCX进行了验证[4],证明CADIS方法能够提升反应堆屏蔽问题的计算效率。

在实际应用中,NECP-MCX遇到了新的挑战,为解决这些挑战,NECP实验室进行了多种理论方法探究和软件功能开发,并于2023年4月发布了NECP-MCX V1.8,该版本主要包括以下新增方法和功能。

对于km尺度的大空间伽马辐射输运问题,由于几何尺寸大,目标计数区域相对整个几何尺寸较小,很难有粒子到达目标计数区域。这类问题一般采用下次事件估计器[5-6](NEE)进行计数,但NEE的统计方差随着粒子数的增加存在波动,难以判断计算结果是否可信,提出CADIS-NEE耦合方法[7],引导粒子在目标计数区域附近碰撞,解决统计方差随粒子数波动的问题。

针对聚变堆的源项及停堆剂量计算,采用粒子输运-燃耗-活化-源项耦合分析方法[8],使用基于反应率修正的预估-校正方法获得燃耗/活化后的材料信息,使用放射性核素的衰变常量、原子核密度和材料区体积计算得到放射性活度,再根据每个核素的衰变光子产额求解衰变光子源项,最后使用衰变光子源项进行稳态光子输运计算获得停堆剂量,能够有效获得PF线圈、TF线圈、真空室和偏滤器处停堆剂量随停堆时间的变化。

对于点源屏蔽问题,常用的CADIS方法中的源偏倚无法对点源进行有效空间偏倚,因此仅由CADIS方法中的权窗起降方差作用,效果不佳。为了保证CADIS方法的有效性并在点源屏蔽问题上进一步降低统计方差,提出首次碰撞源(FCS)-CADIS方法[9],将点源转换为分布在全空间区域中的首次碰撞源,有效利用CADIS方法中的源偏倚,达到更优的降方差效果。

此外,NECP-MCX V1.8还新增了随机介质模拟[10]、面源续算、通用源定义、广义敏感性分析[11]、点核积分计算[12]等功能。

本文重点介绍CADIS与Forward(FW)-CADIS方法、CADIS-NEE耦合方法、输运-燃耗-活化-源项耦合分析和FCS-CADIS耦合方法的理论模型及其应用。

1 理论方法

1.1 CADIS与FW-CADIS方法

CADIS方法通过求解共轭输运方程获得共轭通量密度,将共轭通量密度作为重要性参数同时生成权窗参数和源偏倚参数,保证了权窗参数和源偏倚参数的一致性,使源粒子产生后落在合理的权窗区间内,从而避免源粒子在产生后进行大量的赌和分裂操作。CADIS方法需要求解的共轭形式输运方程可表示为:

φ*(r,E′,Ω′)dΩ′dE′=q*(r,E,Ω)

(1)

式中:φ*(r,E,Ω)为对应共轭源q*(r,E,Ω)的共轭通量密度;Ω、Ω′为粒子入射飞行方向和出射飞行方向;r为空间位置;E、E′为入射能量和出射能量;Σt为宏观总截面;Σs为宏观散射截面。

根据CADIS理论,可将目标响应量计算公式中的响应函数Σd设置为共轭源以求解共轭通量密度,目标响应量R的计算公式为:

(2)

式中:V为探测器体积;φ为前向通量密度。

根据共轭通量密度设置源偏倚参数,偏倚后的源抽样概率密度函数为:

(3)

为保证无偏性,对偏倚后粒子权重(wgt)进行调整:

(4)

式中,wgt0为偏倚前的粒子权重。

对应权窗下界的设置表示为:

(5)

式中:Cu为权窗上界乘数;wl为权窗下界。

FW-CADIS方法可以针对多响应进行重要性抽样,达到多响应同时降方差的效果。相比CADIS方法,FW-CADIS需要多进行1次前向计算获得前向通量密度,对目标量的响应函数Σd进行加权生成共轭源q*:

(6)

后续的操作流程与CADIS方法一致。

1.2 CADIS-NEE耦合方法

NEE包括点探测器和环探测器,通过确定性地估计事件对通量密度的贡献来获得通量密度计数值。事件对计数的贡献可分为源发射的贡献和每次碰撞事件的贡献,统一表示为:

(7)

式中:r0为探测器点的空间位置;w为粒子权重;p(Ω)为碰撞后朝Ω飞行的概率密度函数值;l为从r飞行到r0的路径长度。

CADIS-NEE耦合方法将CADIS方法和NEE耦合,CADIS的源偏倚影响NEE中源发射事件对目标计数的贡献,CADIS的权窗影响NEE中碰撞事件对目标计数的贡献,引导粒子向目标计数点偏倚输运,最终达到降低NEE方差的目的。CADIS-NEE耦合方法的流程图如图1所示,首先进行CADIS流程计算出源偏倚参数和权窗参数,然后进行粒子的输运模拟,在模拟过程中考虑从源粒子到目标计数点的贡献和从碰撞到目标计数点的贡献。

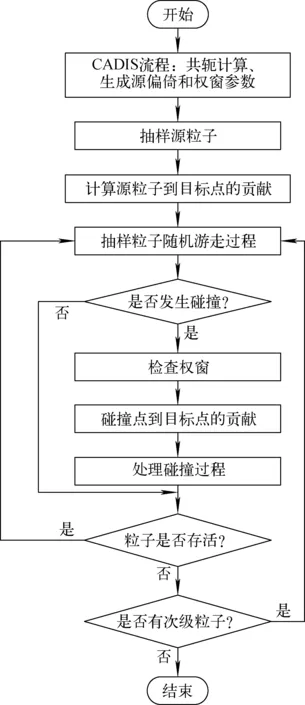
图1 CADIS-NEE耦合方法流程图[7]Fig.1 Flow chart of CADIS-NEE method[7]

1.3 聚变堆停堆剂量计算方法

目前聚变堆停堆剂量计算面临如下问题:传统的质能转移统计方法的精度较低,该方法假定了入射的初级光子的所有能量均沉积在被吸收的位置,不符合真实的物理过程;聚变堆燃耗分析中未考虑活化过程的影响导致的精度较低,需要进行粒子输运-燃耗-活化耦合求解;聚变堆源项分析中活化计算忽略了中子能谱随时间变化导致的精度较低。针对以上问题,NECP-MCX开发了粒子输运-燃耗-活化-源项耦合分析方法,方法流程如图2所示。

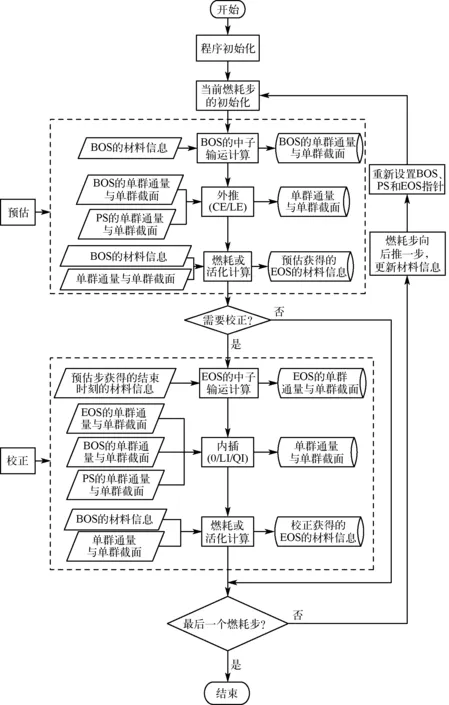
图2 粒子输运-燃耗-活化-源项耦合分析方法流程图[8]Fig.2 Flow chart of neutron-transport/depletion/ activation/source-term coupling analysis[8]

1.4 FCS-CADIS方法

在常见的屏蔽深穿透问题中,源区域和目标区域之间的厚屏蔽层是导致蒙特卡罗源粒子难以输运到目标计数区域的主要原因。CADIS方法中的源偏倚和权窗分别对源粒子生成和粒子输运过程进行了偏倚抽样操作,源偏倚让源粒子偏向目标区域生成,权窗让粒子在输运过程中靠近目标区域尽可能地分裂,远离目标区域的用轮盘赌终止,达到增加目标区域粒子数目的目的。但是CADIS方法的源偏倚对于小区域源或近似点源问题具有局限性,主要原因是小区域源或近似点源的源空间分布区域相对整个问题几何区域太小,CADIS的源偏倚对此类源进行空间偏倚的效果十分有限,导致CADIS方法效果欠佳。FCS-CADIS方法对初始源进行一次输运和碰撞操作,生成分布在整个问题区域的首次碰撞源,对首次碰撞源进行源偏倚操作,可有效提升源偏倚的空间偏倚效果。FCS-CADIS方法的首次碰撞源生成操作如下所示:

φ(r,E,Ω)=φu(r,E,Ω)+φc(r,E,Ω)

(8)

式中,某一相空间区域(r,E,Ω)处的通量密度可以拆分为从由源发射未经碰撞的贡献部分和经过一系列碰撞过程的贡献部分,即未碰撞通量密度φu和碰撞通量密度φc。

使用未碰撞通量密度进行一次散射处理可得到首次碰撞源Sfcs(r,E,Ω):

E,Ω)φu(r,E′,Ω′)dE′dΩ′

(9)

式中,Σs(r;E′,Ω′→E,Ω)为散射截面。

对于首次碰撞源抽样进行输运模拟计数得到的通量密度即为碰撞通量密度φc(r,E,Ω),此过程为固定源计算,使用CADIS方法进行降方差,最终得到的碰撞通量密度即为减方差后的碰撞通量密度。将碰撞通量密度φc和未碰撞通量密度φu相加,得到完整的通量密度,该耦合方法即为FCS-CADIS方法。

2 应用验证

2.1 PCA屏蔽装置

PCA-Replica算例[13]模拟一个压力容器的屏蔽问题,计算不同屏蔽深度下的中子能谱和探测器中的反应率。PCA-Replica算例的源来自于一个堆芯,使用一个高富集度的裂变板代替堆芯源。该算例在NECP-MCX中建模的x-z截面如图3所示。分别使用NECP-MCX直接蒙特卡罗计算、CADIS方法和FW-CADIS方法计算10个探测器位置上的计数。其中CADIS方法将距离源最远的探测器设置为共轭源,3种方法的计数结果分别命名为MCX_direct、MCX_cadis10和MCX_fwcadis。将计算得到的各反应道对应的反应率和实验值对比得到C/E,同时对比各计数的相对标准偏差(RSD)和品质因子(FOM)。PCA-Replica算例中所有探测器处反应率的C/E[14]如图4所示,所有探测器处反应率计数的相对标准偏差[14]如图5所示,所有探测器处反应率计数的FOM[14]如图6所示。将各探测器按照距离源由近到远分别编号为1～10号,在图4、5中,序号1～16号表示各探测器的反应率计数,其中序号1～10为1～10号探测器的103Rh(n,n′)反应率计数,序号11～13为8～10号探测器的115In(n,n′)反应率计数,序号14～16为8～10号探测器的32S(n,p)反应率计数。在以下所有应用验证中,涉及CADIS方法和CADIS-NEE方法的FOM计算均考虑了SN的计算时间,且SN计算与蒙特卡罗计算所用的CPU核数相同。

图3 PCA-Replica算例截面模型图[14]Fig.3 Cross section model of PCA-Replica benchmark[14]

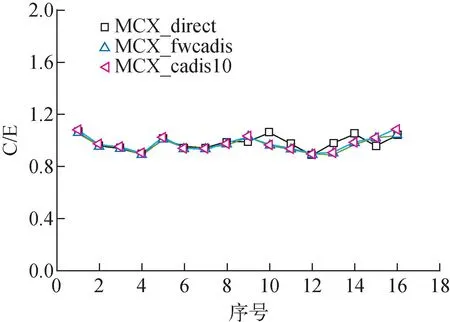
图4 PCA-Replica算例中探测器处反应率的C/E[14]Fig.4 C/E of reaction rate at all detectors in PCA-Replica benchmark[14]

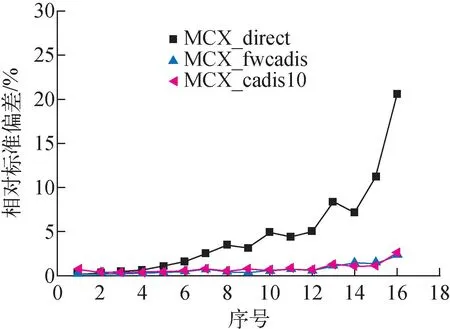
图5 PCA-Replica算例中探测器处反应率计数的相对标准偏差[14]Fig.5 Relative standard deviation of reaction rate count at all detectors in PCA-Replica benchmark[14]

图6 PCA-Replica算例中探测器处反应率计数的品质因子[14]Fig.6 FOM of reaction rate count at all detectors in PCA-Replica benchmark[14]

由图4可知,NECP-MCX程序中的蒙特卡罗直接计算、CADIS方法和FW-CADIS方法均正确,在每个探测器处的计算结果与实验值偏差不大。由图5可知,使用CADIS方法和FW-CADIS方法均能够有效降低各探测器位置处的相对标准偏差,相对标准偏差均在5%以下。由图6可知:将距离源最远的探测器设置为共轭源的CADIS方法能够提升远离源的探测点处的计算效率,而靠近源处的计算效率低于蒙特卡罗直接计算;FW-CADIS方法能够同时提高多个探测点处计算效率,并且提升效果最显著,相较蒙特卡罗直接计算,各探测点处的FOM平均提升80倍,最大提升168倍。

2.2 大空间伽马辐射输运模拟

大空间伽马辐射输运问题常见于大空腔或大空气介质区域的辐射输运环境。大空间伽马辐射输运问题由于其几何尺寸较大,通常从源到探测点的光学距离超过10个平均自由程,通量密度下降超过8个数量级以上,属于深穿透问题。而由于几何尺寸大,目标计数区域相对整个几何尺寸较小,很难有粒子到达目标计数区域,常用的径迹长度估计和碰撞估计难以有效计数,因此对于小计数区域问题通常使用NEE。本文的大空间伽马辐射输运模型如图7所示,整个模型为简化山体模型,伽马光子源位于距离地面H1=1 000 m处,山体高度H2=500 m,宽度为L2=1 000 m,目标计数区与源的水平距离约为L1=2 000 m。

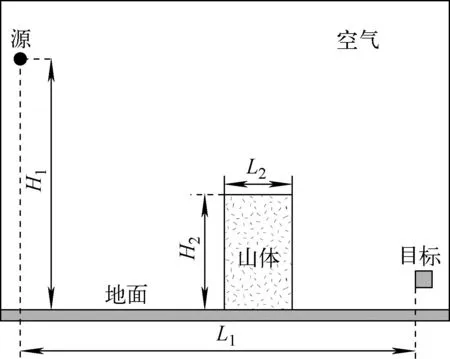
图7 大空间伽马辐射输运问题几何模型Fig.7 Geometry of large-space gamma radiation transport problem

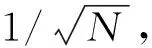
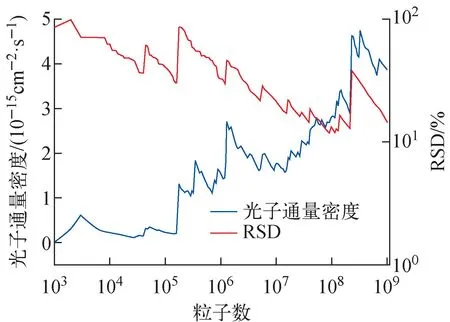
图8 NEE方法计算的光子通量密度与相对标准偏差Fig.8 Photon flux density and relative standard deviation of NEE method

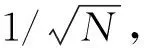
表1 CADIS-NEE和NEE方法的计算时间、RSD和FOMTable 1 Calculation time, RSD and FOM of CADIS-NEE and NEE methods

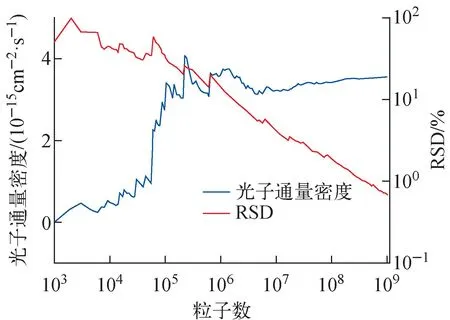
图9 CADIS-NEE耦合方法计算的光子通量密度及其相对标准偏差Fig.9 Photon flux density and relative standarddeviation of CADIS-NEE method

2.3 CFETR停堆剂量计算

中国聚变工程试验堆(CFETR)的模型示意图如图10所示,在NECP-MCX建模中,为了真实地反应中子通量密度及光子通量密度在CFETR的真空室、TF线圈等结构的环向上分布的不均匀性,按照包层模块的轮廓线,将CFETR的真空室、TF线圈等所有外围部件切割成34份,模型如图11所示。

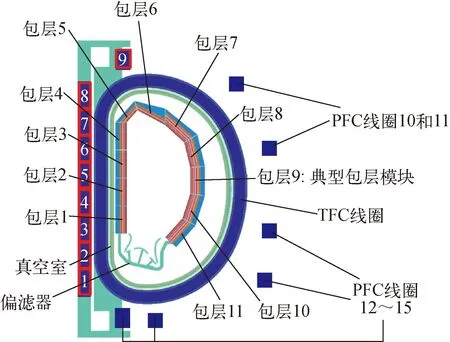
图10 CFETR模型示意图[8]Fig.10 Model scheme of CFETR[8]

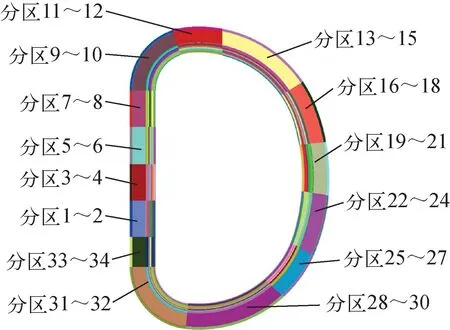
图11 CFETR外围部件沿环向方向的切割方式及编号[8]Fig.11 Partition modeling and numbering of CFETR outer part along circumferential direction[8]

对CFETR进行粒子输运-燃耗-活化-源项耦合计算,以获得CFETR的燃耗特性,并对每个停堆时间点上的源项和停堆剂量进行计算。CFETR的氚增殖比(TBR)燃耗计算结果如图12所示。如果采用传统的燃耗计算不考虑活化计算的计算方法,TBR从初始装料的1.170 4下降到第16年的1.163 6,下降了0.006 8;如果采用更贴近工程运行实际的粒子输运-燃耗-活化-源项耦合分析方法,并考虑Be区域活化过程,TBR从开始装料的1.170 4下降到第16年的1.147 3,下降了0.023 1。传统的燃耗计算不考虑活化计算,计算方法低估了TBR的下降速率。由于TBR下降至限值(TBRlimit)后需对CFETR进行换料,因此TBR的下降速率与CFETR的换料周期呈反比关系。由于各国对聚变堆包层的TBRlimit不同,本文假设CFETR的TBRlimit为1.10。按照传统的计算方法获得的TBR下降速率外推,CFETR的换料周期约为83 EFPY。按照粒子输运-燃耗-活化-源项耦合分析方法获得的TBR下降速率外推,CFETR的换料周期约为25 EFPY。因此,传统的计算方法高估了CFETR的换料周期。

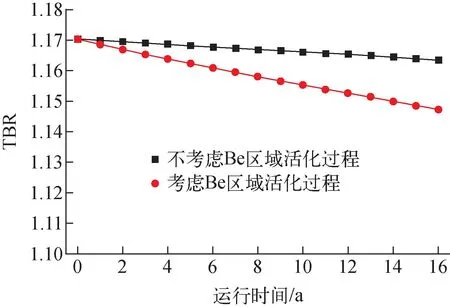
图12 不同计算方法的TBR燃耗曲线[8]Fig.12 TBR depletion curve using different calculation methods[8]

将CFETR停堆后的活度变化划分为5个阶段,时间点依次为刚停堆、停堆1 d、停堆5 a、停堆50 a、停堆250 a以及停堆500 a。图13示出以栅元为计算单元获得的CFETR中包层、偏滤器、真空室及极向屏蔽层、TF线圈和PF线圈以及PF线圈支撑肋、全堆总的衰变光子源强随时间的变化。图14示出这些时间点上,以网格为基础获得的衰变光子源项的相对分布。

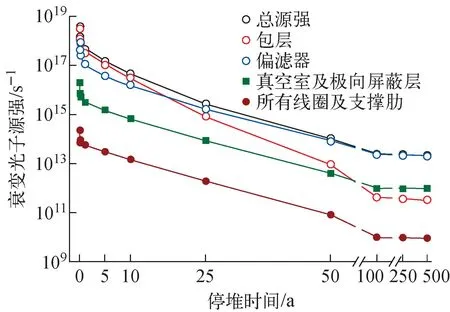
图13 停堆后的光子源强[8]Fig.13 Decay photon strength after shutdown[8]

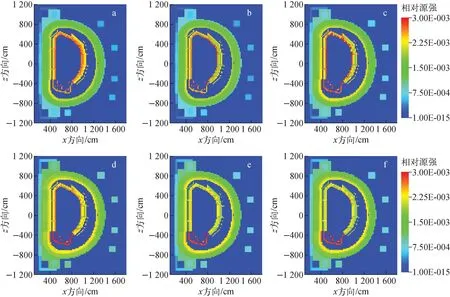
a——刚停堆;b——停堆1 d;c——停堆5 a;d——停堆50 a;e——停堆250 a;f——停堆500 a图14 CFETR全堆衰变光子源项的相对分布[8]Fig.14 Relative distribution of CFETR decay photon source[8]

基于源分布文件,使用NECP-MCX进行光子输运计算,并使用国际辐射防护委员会(ICRP)提供的通量剂量转换因子进行统计,获得CFETR全堆的停堆剂量分布。图15示出单个典型包层模块(即包层9处的单个模块)内、TF线圈处、真空室处和偏滤器处的停堆剂量随停堆时间的变化。

基于CFETR的输运-燃耗-活化-源项耦合计算证明NECP-MCX具有对聚变堆进行输运-燃耗-活化-源项耦合分析的能力,能够有效获得PF线圈、TF线圈、真空室和偏滤器处停堆剂量随停堆时间的变化。

2.4 点源屏蔽问题模拟

设置如图16的点源屏蔽问题简化模型,中子源在1 cm×1 cm×1 cm的空间上均匀分布,相对整个问题几何较小,可视为点源进行处理。

图16 点源屏蔽问题[9]Fig.16 Point source shielding problem[9]

分别使用FCS方法、蒙特卡罗直接计算、FCS-CADIS方法进行计算,统计从源区出发由近到远不同距离下的中子通量密度,将投入更多粒子数的CADIS方法计算结果作为参考解,结果如图17所示。根据中子通量密度的计算结果,蒙特卡罗方法在靠近源区的位置与参考解的误差较小,而FCS和FCS-CADIS方法与参考解的偏差较大,这是因为FCS和FCS-CADIS方法对源区作了点源近似,且在首次碰撞源生成时有空间上的网格化处理和能量的多群处理;随着离源区的距离增加,FCS-CADIS方法与参考解偏差变得较小并且稳定,而FCS方法和蒙特卡罗方法与参考解的偏差较大且不稳定。表征计算效率的FOM结果如图18所示,在距离源区较远的区域FCS-CADIS方法的FOM有明显优势,比CADIS方法高2倍,符合理论预期,也表明在远离源区的区域,FCS-CADIS方法具有最高计算效率的优势。

图17 不同距离下的通量密度计算结果[9]Fig.17 Flux density result at different distances[9]

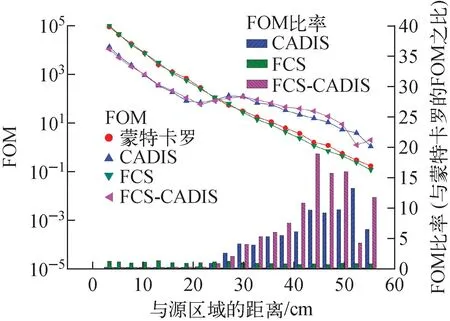
图18 不同距离下的品质因子[9]Fig.18 FOM result at different distances[9]

3 结论

西安交通大学计算物理实验室研发了深穿透跨尺度辐射场软件NECP-MCX,在软件中实现了全自动的FW-CADIS方法,在PCA屏蔽装置上进行了验证,相较蒙特卡罗直接计算方法,FW-CADIS方法在各探测点处计数效率平均提升80倍,最大提升168倍;提出了CADIS-NEE耦合方法,解决了大空间伽马射线辐射输运模拟中粒子难以甚至无法到达探测区域的问题,改进了传统的NEE方法,在简化山体屏蔽模型上,CADIS-NEE耦合的计算结果比传统的NEE方法效率更高,是其6.8倍,且数值结果更稳定;开发的粒子输运-燃耗-活化-源项耦合分析方法提高了聚变堆停堆剂量模拟精度,能够有效获得PF线圈、TF线圈、真空室和偏滤器处停堆剂量随停堆时间的变化;新增的FCS-CADIS耦合方法,针对近似点源屏蔽的模拟,进一步提高了计算效率,将远离源区的计数效率提升2倍。