数学史浸润课堂：小学数学学科育人的实施路径

江苏南京市江宁区秣陵中心小学（211100） 管婷婷

数学是研究数量关系和空间形式的一门学科。纵观数学史，数学知识都经历了推理、诞生以及继承创新和互相包容的过程。将数学史引入小学数学课堂，可深化数学史与数学教育的关系，对发挥数学学科的育人功能、落实立德树人的根本任务具有重要意义。

一、数学史育人功能

《义务教育数学课程标准（2022 年版）》（以下简称《课程标准》）指出，教材编修要注重教材创新，展现数学发展史中伟大数学家，特别是中国古代与近现代著名数学家，以及他们的数学成果在人类文明发展中的作用，增强学生的爱国情怀和民族自豪感。

（一）增强学生的文化自信

立德树人是当代教师教育教学工作的根本任务。教师要围绕学科育人的目标进行教学。数学史不仅包含重要的数学知识与结论，还有着丰富的数学文化韵味。另外，数学史中蕴藏着“育人”的关键要素——学生能感受到前人在探索数学知识的过程中永不放弃、坚持钻研、合作探索的精神。在数学课堂中融入中国数学史，能让课堂散发理性的光辉与人文气息。经过这样的学习，学生会增强文化自信及民族自豪感。

（二）提升学生的数学素养

了解数学史有助于学生理解数学知识。了解相关概念、公式的发展历程后，学生可以借鉴数学家们的研究方法对知识重难点进行深入研究，从而加深认识。学生在学习过程中逐步打破原有的数学思维方式，将已有的结论放到新时代中去“完整”地学，在传承中进行突破、创新，不断完善数学思维，发展核心素养。

（三）活化教师课堂教学

要想让数学史更好地浸润数学课堂，教师不仅要把握好数学史的内容选择、呈现方式和呈现时机，还要不断地学习数学史，尝试将知识的原始样态与现今的发展成果进行关联，深入剖析知识发展的节点，解决学生学习的痛点。“以史为鉴”，若教师能从历史经验中汲取智慧，那教学时方向将会更加清晰，也能更好地处理学生在学习上遇到的困难。

二、数学史浸润课堂的现实困境

（一）部分教师对数学史的理解有偏差

部分教师将数学史当作简单的数学阅读材料，在课的开始或结束如蜻蜓点水般一笔带过，致使学生只是大致了解故事的梗概，没有深入体会其内涵。还有的教师将数学史视作课堂的备选知识，或者将其安排在可有可无的拓展环节，或者粗暴地堆砌数学史料，没有挖掘数学史的育人价值。数学史的教学不应是简单的知识科普，也不应是说故事般的教学，教师要深入学习数学史，不断丰富自身的知识储备，将数学史灵活运用于教学中，让其中的数学精神与文化内涵润泽学生的数学学习。

（二）数学史融入课堂的形式单一

笔者深入课堂后发现，多数教师已有在课堂中融入数学史的意识，但将数学史融入教学的形式还是比较单一，令学生感觉枯燥乏味。数学教育家张奠宙指出，当前的数学教学往往局限于概念、定理和思想等局部历史的介绍，缺乏宏观历史进程的综合性描述，但后者才是揭示数学含义、加深数学知识文化理解的关键所在。那么，数学史在何时融入、怎么融入？这是值得广大教师思考的问题。

（三）数学史教学脱离育人意义

现阶段数学史的教学局限于数学历史文化的熏陶，这样的数学史教学以欣赏为主，是浮于表面的。为了让数学史的呈现不再是简短的口头介绍或者看一段视频，教师应重视数学史中另一关键要素——经验，以前人的经验为知识发展的线索，并着眼于《课程标准》，基于教材且敢于跳脱出教材，真正为学生的发展而教。

三、数学史浸润课堂的实践路径

（一）“倒转”历史，体现知识之谐

北京师范大学教育学院郭华教授曾提出数学教学中的“两次倒转”机制。第一次“倒转”，从内容上看体现在“学生认识的起点是前人认识的终点”，即学生习得的经验是传承与延续先贤的智慧成果；第二次“倒转”，从过程上看是学生在活动中经历知识的发展，即学生在教师的引导下“重走”历史，这是一个将浓缩的知识重新引入课堂的过程，重在让学生经历知识的形成过程，实现知识的建构。

1.圆，一中同长也

在历史上的很长一段时间内，人们都困惑于圆周长与直径的比值究竟是多少。中国古代数学著作《周髀算经》中有“周三径一”的说法；刘徽用“割圆术”求得圆周率为3.1416；祖冲之求出圆周率的近似值在3.1415926 和3.1415927 之间；1706 年，数学家威廉·琼斯最先使用希腊字母“π”来表示圆周长与直径的比值，即圆周率。教师将这些数学史融入课堂，让学生知道圆周长公式的推导经历了从有限分割到无限分割，从而深刻体会“无限分割、化曲为直”的思想方法。

2.数，起源于数

在学生初识分数时，教师要回望分数的历史起源，引导学生关注分数“部分与整体”的意义。以“认识几分之一”为例，古人在分物品时，除了平均分给2 个人，还会分给3 个人、4 个人……因此，“几分之一”的教学除了从二分之一引入，还可以从四分之一入手，使教学内容更加贴合多样的生活实际。

3.直，叁（三点）也

古人发现“鸟”的飞行可以超脱于其所在的平面，且鸟在一定高度上可以沿直线飞行，根据这一现象，为了强调直线的距离很长，人们便用“鸟道”来描述直线距离，意在突出“长”。后来，各派学者们又运用了“鸟飞准绳”的概念，强调“直”的重要性。再后来，《墨子》一书中这样描述：“三点共线即为直线。”

（二）具身经验唤醒知识之源

为了让学生从数学史中深刻感受古人认识“线”的历程，笔者尝试以具身经验“倒转”至知识的起源，让学生在操作中获得具身认知。

数学知识来源于人们的生产生活，如中华传统文化的“六艺”——射、御、礼、乐、书、数，其中的“数”就是指数学知识。因此，当学生在探索数学知识的过程中出现“词不达意”的情况时，教师可以引导学生用比画、画图等方式来表示。

具身认知可以让学生重走古人在劳动实践中发现知识的过程，实现数学知识与生活经验的互融共生。如《孔子家语》有云：“夫布指知寸，布手知尺，舒肘知寻，斯不远之则也。”寸、尺、寻这样的长度单位是通过具身操作建立的，这便是身体尺。教师在教学时融入这段史料，能让学生对身体尺的认识更深刻。

以“直线、射线和角”一课为例，笔者试着“不走寻常路”，用身体操作代替以往教学中的画线段以及线段两次延长的过程。依据具身认知的理念，笔者先通过情境唤醒学生对线段的认知，再基于学生已有的“比大小”“比多少”“比长短”的经验，以学生想着再“长一些”的认知需求为契机，正向引导，唤醒学生的身体“细胞”。对于生活中很难体会到的“无限长”，则让学生不断地向身体两侧移动拳头，感受这样比画出来的长度有限。通过几个人手牵手，学生发现能找到更长的长度，而随着人数增多，学生便会脱口而出“无限长”。“直线、射线和角”一课完整的具身体验教学活动流程如图1所示。

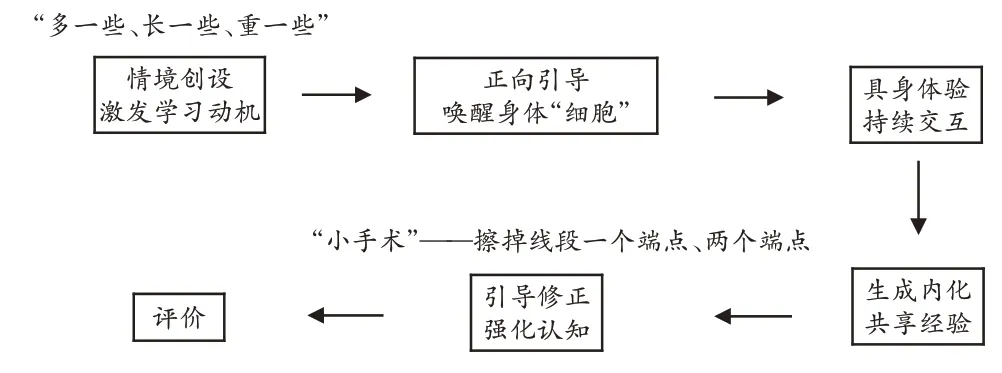
图1

（三）高阶任务重现经典时刻

以史为鉴，方能确保知识的学习水到渠成。在教学“第二次倒转”前，教师要精心筛选史料。

以“圆的周长”为例，笔者的教学过程如下。

师：这里有2个圆，哪个圆的周长大？再观察2个圆的直径，哪个圆的直径大？对比圆的直径和周长，你发现了什么？

生1：直径越大，周长越大。

师：怎么量出圆的周长呢？

生2：可以先用一条线沿着圆的边线围一圈，再量出所用的线的长度。

生3：在圆上做标记，以直尺的0刻度线为起点将圆沿直线滚动一圈，滚动的距离即为圆的周长。

师：你们说的这两种方法都是将围成圆的曲线化为直线，这种转化数学上称之为“化曲为直”。我们知道正方形的周长是边长的4 倍。圆的周长与直径是否存在倍数关系呢？先做一做（如图2），再说一说。

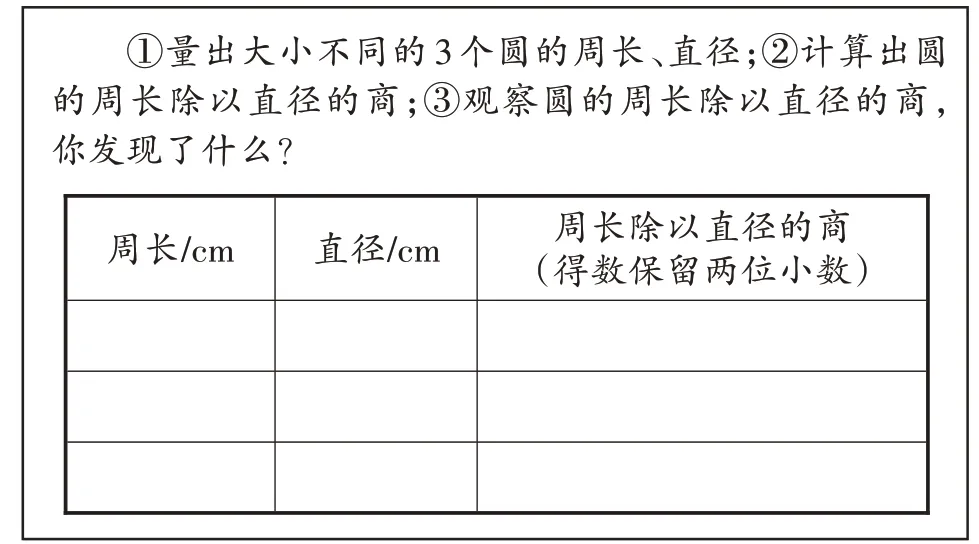
图2

生4：3 个圆的周长除以直径的商都是3 倍多一些。

师：数学是一门严谨的学科，所有圆的周长都比直径的3倍大一些吗？

笔者通过两个数学活动将浓缩的圆周率的数学史在一节课中慢慢“泡”开，让学生得以“细品”与“回味”。另外，在带领学生探索圆的直径与周长的关系时，笔者将教材的例题呈现顺序进行了两处改编。

第一处改编是将教材中例4 的情境改为直接呈现2 个大小不同的圆，以简洁清晰的环节介绍圆的周长的含义，指出圆的周长与直径的关系。这一改编避免了教学中可能出现的无关信息的干扰——英寸和厘米的转换问题，以及将轮胎滚动一周的长度转化为周长（空间想象）的问题。直接出示2 个大小不同的圆，学生就能很明显看出大圆的周长大。学生通过对比2 个圆的直径的大小很容易得出：圆的直径越大，周长越大。将“轮胎滚动一周的长度就是圆的周长”这一知识点调整为“绕圆法”“滚圆法”后，也与“圆”的数学史发展进程一致。

第二处改编是实验探究圆的周长除以直径的商的规律，再通过对比，学生一致得出：圆的周长总是比直径的3倍大一些。

从归纳推理到演绎推理，由“易”到“难”，这更符合学生的学习规律，也更贴合数学史上古人发现圆的周长与直径之间的倍数关系的过程。

又如，在“认识几分之一”一课中，笔者带领学生经历分数的“第二次倒转”，在引入分数时重现分数起源的关键步骤。如在“吃饼”的教学情境中，从“吃2 个饼没饱”到“再吃1 个饼，吃不完一整个，但是还想再吃一小块”，引导学生用一句话或一个数来表示，让别人一听就知道这一小块饼是多大。学生的思维是发散的，每个人对“一小块”的理解不一样。有人说：“一小块比较小，可以看作是一个饼的四分之一。”笔者及时捕捉学生交流中出现的“四分之一”，紧扣四分之一中“四”与“一”的含义，引导学生理解部分与整体的关系，从而构建分数的意义。

在形成概念的过程中，教师要紧扣“以史为鉴”，同时鼓励学生将数学史进行“再创造”，经历知识内化过程中的“重演”“评判”“选择”（如图3），让学生真正收获知识。

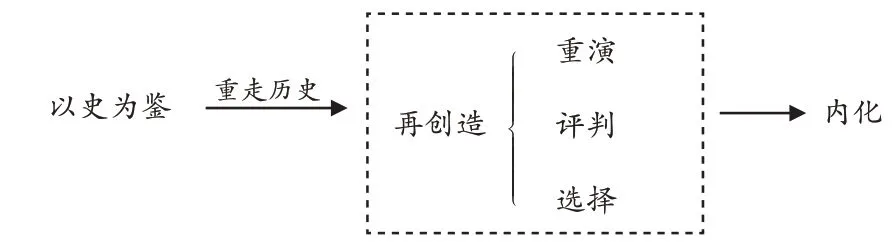
图3

在“圆的周长”一课即将结束前，笔者没有立即进行习题检测，而是让学生欣赏“圆周率钢琴曲”。在美妙的音乐中，人类探索圆周率的一幕幕如电影般浮现在学生眼前。学生沉浸其中，不断地回味这节课的学习过程。

数学史中有精彩的故事，也有具体的人——杰出的数学家，以及数学家的探究精神。将数学史浸润课堂，不仅能让学生得到数学文化的熏陶，增强文化自信和民族自豪感，还能让学生感悟数学家的人格魅力，树立学好数学的信心，树立为数学学科发展做贡献的远大志向。如此，数学的“学科育人”才是真正落到实处。