2023年新高考Ⅱ卷第21题的推广探究*
湖南省长沙市雷锋学校 (410217) 邓捷敏 童继稀
本文通过对2023年新高考Ⅱ卷中的第21题,即解析几何大题的分析,将试题结论推广到一般情形,并类比、归纳与推理,将结论拓展到椭圆与圆中,从而得到有心圆锥曲线的一组统一性质.
一、试题呈现与反思
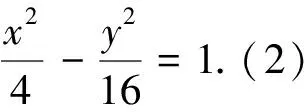
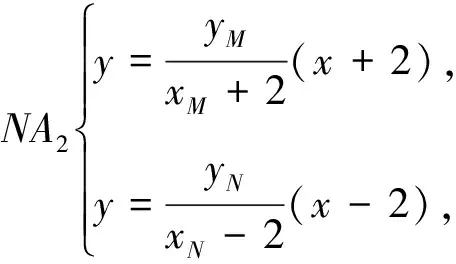
本题根据解析几何研究的两个基本问题来进行设计,即第(1)问是根据条件求曲线方程,第(2)问是根据曲线方程来研究性质.有趣的是两条直线的交点P在垂直于x轴的定直线上,从而引发我们产生以下疑问:
问题1 为什么题意中强调直线MN与双曲线相交于左支呢?如果相交于两支,点P是否还在定直线上?
问题2 直线MN可否过双曲线焦点所在轴上的任意一定点?
问题3 试题中的结论在一般的双曲线中是否也成立?该结论的逆命题是否成立?
问题4在其他圆锥曲线中是否也有类似结论?
以下对这4个疑问进行综合探究.
二、结论推广与拓展
将问题1、问题2与问题3放在一起考虑,经探究,可得如下结论:

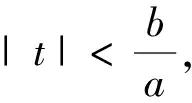

当双曲线焦点和点D在y轴上时,有相同结论如下:

若将性质1的条件与结论互换,即逆命题也成立.

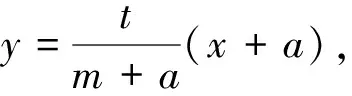
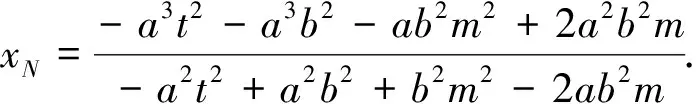
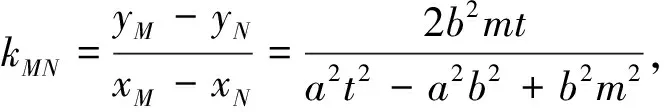
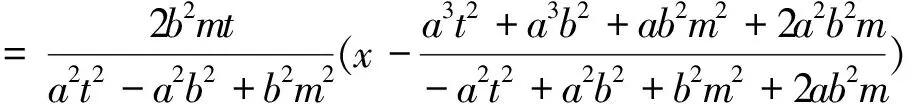
根据图形的对称性,若直线MN过定点,则定点必在x轴上.令方程①中的y=0,则
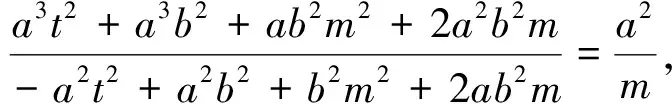
将性质1类比到焦点在x轴上的椭圆中时,可得如下3个类似的结论:

当椭圆焦点和点D在y轴上时,有相同结论如下:


令性质3中的a=b,从而得到圆中的一个类似结论:

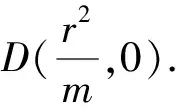
以上性质的证明与性质1、性质2类似,读者可自行证明.
三、结语
本文在类比、归纳与推理的研究过程中,对圆锥曲线的性质进行推广与拓展,得到了一般性的结论.类比、归纳与推理是研究数学问题的常见方法,结论推广其实就是类比和归纳的过程,也是数学抽象素养的落实过程.《普通高中数学课程标准(2017版2020年修订)》指出,“数学抽象素养的育人价值在于通过高中数学课程的学习,学生能在情境中抽象出数学概念、命题、方法和体系,积累从具体到抽象的活动经验”[1].如果能把这种活动经验运用在高考复习备考中,让学生体验和经历已知数学命题的推广过程,那么学生就能够在新的情境中选择和运用数学方法解决问题,自然也就能达到提升高考复习备考效果的目的.

