基于任务群的深度学习设计
——以2019人教A版的一道习题为例
广东省广州市天河外国语学校 (510630) 刘惠梅
高中数学新教材中很多习题有着极强的“代表性”与“穿透性”,教师若能积极开展对教材习题的研究,创设合理的任务群,以“最近发展区”为平台,在课堂中提出高价值的问题,就能引导学生仔细观察、大胆猜想,严谨推理,不断拓展学生的认知,提升四基四能.
本文以2019版人教A版选择性必修第一册的一道习题为例,通过聚焦任务群,让学生经历从特殊到一般、从确定性到完备性、从顺推到逆推的探究过程,体验研究数学问题的普适性方法,落实数学核心素养.
具体研究思路为:

一、问题
题源(2019版人教A版选择性必修第一册第三章“圆锥曲线的方程”P128习题3.2第11题)M是一个动点,MA与直线y=x垂直,垂足A位于第一象限,MB与直线y=-x垂直,垂足B位于第四象限.若四边形OAMB(O为原点)的面积为3,求动点M的轨迹方程.
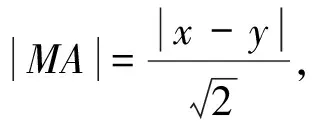
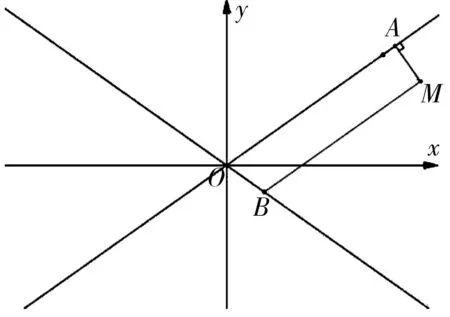
图1
设计意图:题源来自于新教材的课后习题,习题通常蕴含了很多一般性规律.老师要善于钻研教材,强化思维迁移,引导思维向广度和深度拓展延伸,引导学生从解题到解决问题的转变.此题结论是否具有一般性?
二、猜想
任务1 题源中直线y=x与y=-x恰好是动点M的轨迹(即双曲线)的两条渐近线,这个结论是否可以推广到以下一般情况?
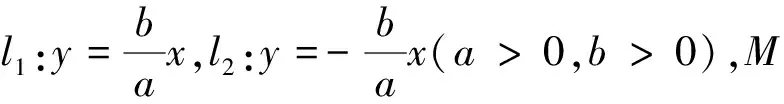
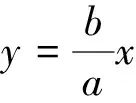
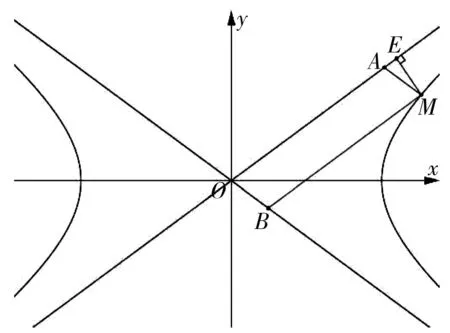
图2

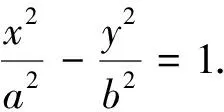
设计意图:任务1将题源中的特殊情况通过大胆猜测、严格证明推广到一般的结论,学生经历从特殊到一般的过程,通过发现隐藏在表象中的一般性结论,实现多题归一.
三、完备性探究
任务2 任务1中若删除“B,A分别在第四、一象限或者二、三象限”,动点M的轨迹会发生变化吗?
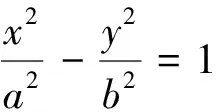
设计意图:任务2针对命题的完备性设计,尊重知识的发生过程,尊重学生的思维发展规律.聚焦任务群,推动学生探究进程,引导学生经历从确定性到完备性的过程,培养思维的严谨性和完备性,提升逻辑推理的数学核心素养.
四、逆命题
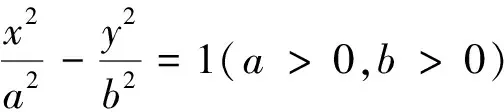
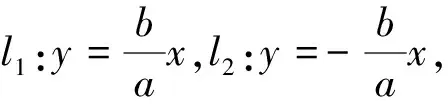
设计意图:深刻理解条件的充分性和必要性是培养学生逻辑推理素养的重点,正难则反,逆推也是提升素养的重要方法.任务3源于教材而高于教材,把基础知识的教学落到实处,学生经历从顺推到逆推的探究过程,培养学生数学运算、逻辑推理等数学核心素养.
五、拓展
部分学生顺着任务群的探究思路,将任务3中的问题稍作改编,得到任务4.
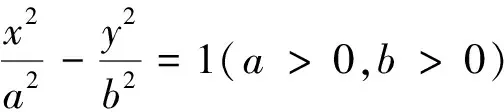
继续深入钻研,以下两个拓展结论的发现自然是水到渠成:
拓展结论1 过双曲线上任一点分别向两条渐近线做垂线,两条垂线段的长度之积为定值.
拓展结论2 已知两条相交的直线,过直线外一点M分别作两直线的垂线,若两条垂线段的长度之积为定值,则动点M的轨迹是以这两条相交的直线为渐近线的双曲线(四支).
设计意图:学生前面经历从特殊到一般,从确定性到完备性,从顺推到逆推的探究过程,体验研究数学问题的普适性方法,在小组合作交流的探究活动中从另一个切入口发现新的规律,提出新的问题,进入新的探究学习.基于建构主义思想,学生将多个知识点串联起来,由已知向未知逐渐扩充,不断扩大知识网络,完善知识网络体系.
高中数学教学中,培养学生的主体意识,激发他们的探究思维能力,能有效提高教学效果,促进数学素养的提升.教学过程中,要重视研究教材中的经典习题,挖掘习题背后蕴含的深层次思想方法,引导学生从解题到解决问题的转变,从单一的机械刷题到落实核心素养的科学训练的转变,丰富学生的方法体系与认知结构.

