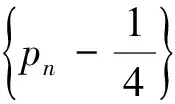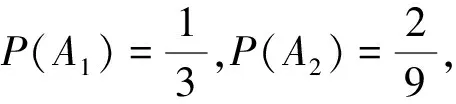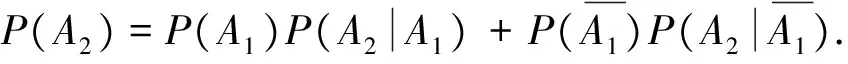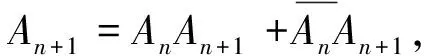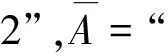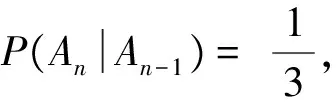聚焦本质试题分析 立足教材变式研究*
——以2023年全国新高考Ⅰ卷理科第21题为例
内江师范学院数学与信息科学学院 (641100) 王 雪 余小芬
概率问题作为高中数学统计与概率领域的核心内容,是高考考查的重点.2023年全国新高考Ⅰ卷理科第21题在数学知识交汇处命题,综合考查全概率公式、随机变量及其分布、数列通项、求和等主干知识,展现内容主线、突出学科本质、凸显数学思维,是一道立意新颖、构思巧妙、研究价值强的典型试题.下文对该试题进行立意、背景、解答及变式分析,以期给教师教学一些启发.
试题呈现甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签决定第一次投篮的人选,第一次投篮的人是甲、乙的概率各为0.5.
(Ⅰ)求第2次投篮的人是乙的概率;
(Ⅱ)求第i次投篮的人是甲的概率;
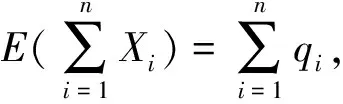
1 试题立意
试题是知识和能力的载体,它体现着考试的目的和内容.[1]从知识考查看,21题以马尔科夫链为背景,以全概率公式为核心,包含互斥事件、概率的加法和乘法公式、离散型随机变量及其分布列、数列递推公式求通项公式、数列求和等高中主干知识,涉及构造法、待定系数法、公式法、类比等重要数学方法,蕴含分类讨论、化归转化、整体等数学思想,体现了数学知识和方法的基础性和综合性.从能力考查看,21题考查数学建模(识别全概率模型、理解两点分布模型)、逻辑推理(理清事件间关系、用构造法及待定系数法求数列通项公式)、数学运算(利用全概率公式、等比数列通项、求和公式、随机变量均值公式计算求解)等数学核心素养.
2 试题背景
试题背景指命题时试题选材的背景.研究试题背景能凸显试题立意、丰富试题研究、导向课堂教学.常见的试题背景有现实背景、教材背景、高考背景、高等数学背景、竞赛背景、数学史背景等.
2.1 高等数学背景
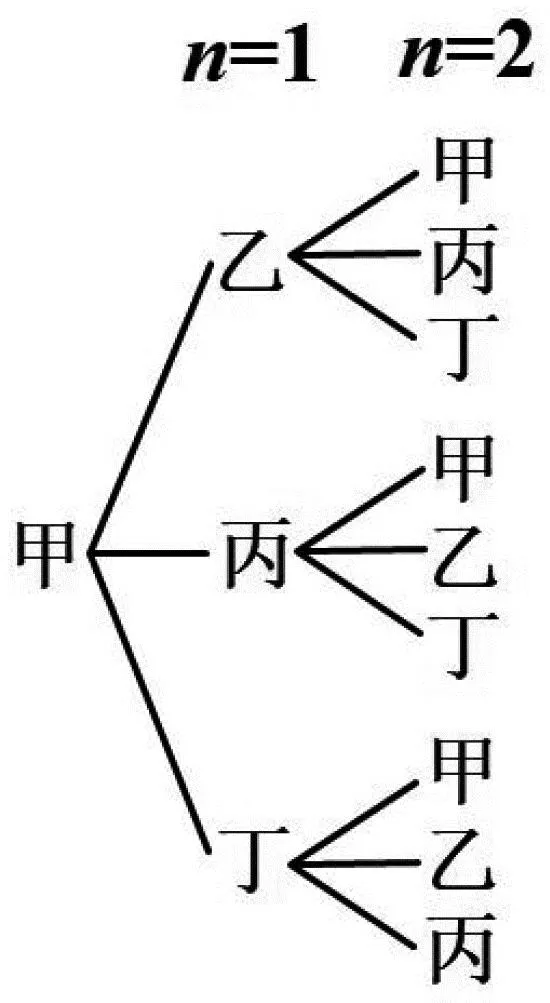
21题蕴含高等数学中马尔科夫链背景.马尔可夫链是概率统计中一个重要模型,其数学定义为:设随机序列{X(n),n=0,1,2,…}具有离散状态空间E.若对于任意m个非负整数n1,n2,…,nm(0≤n1 教材是连接课程方案与教学实践的枢纽,是教师教和学生学的载体.[3]同时,教材也对高考试题的命制具有导向性,是高考试题命题选材的源泉.读完21题,给我们的感觉是似曾相似.确实题目含有教材例习题的影子. 一是源于2019年人教版普通高中数学教科书(下文简称“人教版教材”)选修三第7.1节例4(50页): 某学校有A,B两家餐厅,王同学第1天午餐随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.[4] 二是源于人教版教材选修三复习参考题7第10题(91页):甲、乙、丙三人相互做传球训练,第1次由甲将球传出,传球者都等可能地将球传给另外两个人中的任何一人.求n次传球后球在甲手中的概率.[4] 以上三题均为全概率公式应用问题.其中例4和21题(1)问考查实质相同,只是将问题背景由“选择用餐餐厅”替换成了“选择投篮对象”,解答思路完全一致.10题同21题都考查利用全概率公式表达数列的递推关系,均涉及构造法、待定系数法求通项公式. (2020年高考数学江苏卷第25题)甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2个黑球的概率为pn,恰有1个黑球的概率为qn. (Ⅰ)求p1,q1和p2,q2; (Ⅱ)求2pn+qn与2pn-1+qn-1的递推关系和Xn的数学期望E(Xn)(用n表示). 25题同21题设问形式和解答思路高度一致:均是先求特殊情况的概率取值,再利用全概率公式表达n为一般情形的概率,都涉及数列递推公式求通项公式,最后求解随机变量数学期望.当然,两题也有细微区别:21题“第i-1次投篮的人是甲”与“第i-1次投篮的人是乙”两事件互斥且和为必然事件,是全概率公式中n=2的情形.而25题甲口袋中“恰有2个黑球”,“恰有1个黑球”互斥,但和不为必然事件,还需补充“恰有0个黑球”的情形,考查全概率公式n=3的情形.同时,21题(Ⅲ)问是两点分布模型求随机变量数学期望,而25题(Ⅱ)问随机变量Xn可取0,1,2三种情况,不是两点分布.全概率公式是高中新教材新增内容,是近年高考的重点和热点,除25题外,2019年全国Ⅰ卷理科第21题,2022年全国乙卷理科第10题等均涉及全概率公式的应用. 解析:(Ⅰ)设Ai=“第i次投篮的人是甲”,Bi=“第i次投篮的人是乙”,则Ω=Ai∪Bi,且Ai,Bi互斥,其中i∈N*.由题意,P(A1)=P(B1)=0.5,P(B2|A1)=0.4,P(B2|B1)=0.8,由全概率公式得,P(B2)=P(A1)P(B2|A1)+P(B1)P(B2|B1)=0.5×0.4+0.5×0.8=0.6. 试题变式,既是研究高考试题的重要视角,也是开展试题教学的重要方式.张奠宙先生指出,依靠变式提升演练水准是数学教学的四个特征之一.通过研究试题变式,能深刻揭示试题背后的知识实质,帮助学生形成良好的认知结构,引导学生掌握数学学习研究的方法手段. 变式1 (改编自人教版教材选修三第7.1节例5)甲、乙、丙三人参加趣味投篮活动,甲每次投篮的命中率为0.6,乙和丙每次投篮的命中率均为0.8,已知甲、乙、丙投篮次数分别占总数的25%、30%、45%.投篮开始时,将每人每次的投篮结果分别记录在一张单独的纸条上(所有纸条相同),如“未投中”,“投中”.投篮结束后,再将所有记录纸条放在不透明纸箱中混合均匀. (Ⅰ)任取一张投篮记录纸条,计算“未投中”的概率; (Ⅱ)如果取到的投篮记录纸条是“未投中”,计算它是乙投篮结果的概率. 解析:设B=“任取一张纸条为‘未投中’”,A1=“抽取纸条为甲投篮结果”,A2=“抽取纸条为乙投篮结果”,A3=“抽取纸条为丙投篮结果”,则Ω=A1∪A2∪A3,且A1,A2,A3互斥.由题意,P(A1)=0.25,P(A2)=0.3,P(A3)=0.45,P(B|A1)=0.4,P(B|A2)=P(B|A3)=0.2. (Ⅰ)由全概率公式得,P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)=0.25×0.4+0.3×0.2+0.45×0.2=0.25. 点评:21题考查全概率公式n=2的情形,变式1将互斥事件拓展为三个,适度提升了解答难度.变式1(Ⅱ)问为可靠性问题,考查贝叶斯公式的应用,在21题的基础上丰富了知识考查.贝叶斯公式同全概率公式均是概率论中应用广泛的重要公式.全概率公式表明综合引起结果的各种原因,导致结果出现的可能性的大小.而贝叶斯公式则反映了当结果出现时,它是由某个原因(比如(Ⅱ)问中A2)引起的可能性的大小,常用于可靠性寿命检验、可靠性维护、可靠性设计等.[6] 变式2 (改编自人教版教材选修三复习参考题7第10题)甲、乙、丙、丁四人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外三个人中的任何一人. (Ⅰ)求2次传球后,球经过乙的次数为X,求X的数学期望; 图1 变式3 (改编自中科大少创班初试题)甲、乙两人各有两球,一红一蓝.甲、乙两人做换球训练,一次操作是甲、乙各随机抽一球与对方交换. (Ⅰ)求2次操作后,甲、乙手中均是同色球的概率; (Ⅱ)求n次操作后,甲、乙手中仍各有一红一蓝球的概率pn,n∈N*. 图2 点评:同21题,变式2、3均为全概率公式n=2的情形,即均可利用两个互斥事件(和为必然事件)分割待求事件,但在具体条件概率的求解上,变式3较21题、变式2提升了难度.解答变式3的关键是理解:甲、乙两人各有一红一蓝两球,进行一次换球操作共有4种情况.其中2种情况为红球换红球(或蓝球换蓝球),换球后两人仍各有一红一蓝两球;另2种情况为红球换蓝球(或蓝球换红球),换球后两人手中均是同色球.若甲、乙两人手中均是同色球,则无论如何操作,换球后均是甲、乙两人各有一红一蓝两球. 变式4 (改编自人教版教材选修三第7.1节习题4)有甲和乙两个箱子中各装有10个球,其中甲箱中有5个红球、5个白球,乙箱中有6个红球、4个白球.抛一枚质地均匀的骰子,如果点数为1或2,从甲箱子随机摸出1个球;如果点数为3,4,5,6,从乙箱中随机摸出2个球.(注:摸出的球要放回) (Ⅰ)求摸到白球的概率; (Ⅱ)求累计摸球个数为n的概率pn,n∈N*.2.2 教材背景
2.3 高考背景
3 试题解答
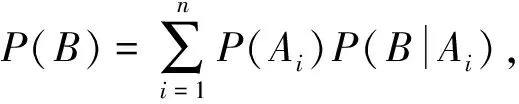
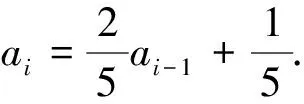

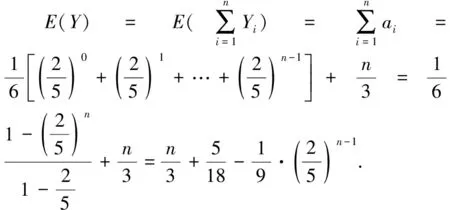
4 试题变式