基于提升数学抽象素养的概念教学设计与实践——以“平面向量的数量积(一)”为例

江苏省苏州工业园区星海实验高级中学 (315100) 唐 秦

数学抽象作为六大核心素养之首,在数学知识的形成和应用中起着至关重要的作用.通过抽象,我们获得了数学概念,数学模型,数学方法,甚至更高层次的数学结构与体系,一切数学对象都可以看成数学抽象的结果.而数学模型、方法、结构等都可以看成在数学概念基础上进一步抽象的结果,因此概念教学是提升高中生数学抽象素养的重要环节.近日笔者在江苏省普通高中校长任职资格班跟岗培训活动中开了一节“平面向量的数量积”公开课,本节课让学生经历了数量积概念及性质的抽象过程,加深了学生对于概念本质的理解,现将本节课的教学过程和教学反思梳理如下.

1 教学内容简析

《向量的数量积》为《普通高中教科书必修第二册》(人教版)第六章第二节第六课时.在此之前,学生已经学习了向量的三种线性运算:向量的加法、减法和数乘.这三种线性运算的研究都是从物理模型出发,抽象出数学概念,接着分别研究运算的相关性质、运算律及应用.本节课类比向量的三种线性运算的研究思路,引导学生从已有经验出发探究向量的数量积,让学生经历平面向量的数量积的概念及性质的抽象过程.

2 教学过程

2.1 复习旧知引入物理模型

问题1同学们,前面我们学习了向量的三种线性运算,请大家回顾一下,这三种线性运算的结果有什么共同的特征?我们研究这三种线性运算的一般思路又是什么?

生:向量的加法、减法和数乘三种线性运算的结果都是向量;对于这三种线性运算的研究都遵循着“物理模型——数学概念(运算的定义)——运算性质——运算律——应用”这一研究思路.

问题2 我们知道向量与向量能够相加、相减,那么能不能相乘呢?类比前面的研究思路,请同学们尝试寻找矢量与矢量相乘的物理模型.

生:物理中的功等于力与力的方向上位移的乘积,而力与位移都是矢量(向量).

师:这里严格来说应该是力和位移两个向量的模的乘积,如果将力和位移分别用F和s表示,则力F所做的功W=|F||s|.

问题3 如果力F和物体位移s方向的夹角为θ.那么力F所做的功为多少?

生:将力F正交分解成物体位移方向上的分力F1和垂直于物体位移方向上的分力F2.因此力F所做的功W=|F1||s|=|F||s|cosθ.

设计意图：向量的数量积既是向量运算体系形成发展的内部需要,又具其物理背景.这里延续向量三种线性运算的研究思路,引导学生主动发现向量数量积的物理模型.

2.2 逐级抽象生成数学概念

问题4 请同学们从运算的对象和结果两个方面,总结“求功运算”的特点.

生:“求功运算”不同于前面所学的三种线性运算,具有如下特点:(1)功W是两个向量F和s的某种运算的结果,而且结果是一个数量;(2)功不仅与两个向量的大小有关,还与它们的方向有关.

问题5从“求功运算”中,可以抽象出怎样的数学运算?

生:将两个向量F和s抽象成a和b,力F和物体位移s方向的夹角θ抽象地看成a和b的夹角,这种新的运算实际上是从a,b得到数量|a||b|cosθ的运算.

师:我们把这种新的运算称为向量的数量积运算,运算的结果称为两个向量的数量积,求功运算就属于向量的数量积运算.事实上,向量的乘积运算除了数量积之外,还有一种向量积运算,这两种运算的定义最初是由Gibbs和Heaviside给出,前者的运算结果为数量,后者的运算结果依然为向量.现在同学们知道这里为什么叫数量积了吧.

问题6 你能给向量的数量积下定义吗?

生:已知两个向量a和b,它们的夹角为θ,我们把数量|a||b|cosθ叫做a和b的数量积(或内积),记做a·b,即a·b=|a||b|cosθ.

设计意图：引导学生从物理模型出发,舍去事物的物理属性,抽取其中的数量关系,从而抽象出向量的数量积运算.然而上述的定义并未交待向量夹角的相关规定,需要进一步地抽象,形成最终的定义.

问题7 在上面的定义中,提到了“两个向量的夹角”的概念,应该如何给“两个向量的夹角”下定义呢?

生:物理模型中的F和s是共起点的,而我们研究的向量都是自由向量,因此可以将两个向量平移至共起点,又cosθ=cos(2π-θ),可以将形成的[0,π]范围内的角看成两个向量的夹角.而我们并没有给出零向量方向的定义,所以两个向量的夹角应该定义在非零向量的基础上.

师:既然两个向量的夹角定义在非零向量的基础上,那么向量的数量积定义应该怎样修改呢?零向量的数量积又应该如何定义?

生:物理模型中的物体在垂直于物体位移方向上的分力F2,垂直方向上的位移为0,而F2对物体所做的功的大小为0,因此零向量与任意向量的数量积为0.

设计意图：进一步引导学生垂直重组已有知识,结合特殊的向量积运算(求功运算),抽象出向量夹角的概念,及对零向量数量积的规定.至此,抽象出了向量的数量积的完整定义.

向量的数量积定义:已知两个非零向量a和b,它们的夹角为θ,我们把数量|a||b|cosθ叫做a和b的数量积(或内积),记做a·b,即a·b=|a||b|·cosθ.我们规定:零向量与任意向量的数量积为0,即0·a=a·0=0.

2.3 从特殊到一般探究性质

如图1,P0是半径为1的半圆弧的中点,点P是该圆弧上的任意一点.

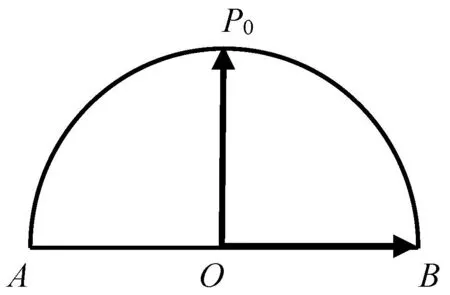
图1

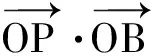
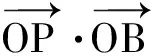
(3)通过前两问的研究,你有哪些发现?这些规律能不能推广?

设计意图：引导学生从两个特殊的向量(单位向量)的数量积出发,把握本质属性,抽象出向量数量积的性质(即弱抽象).

实际授课中,学生抽象出以下性质:

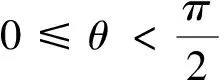
师(结语):同学们,这节课我们探究了向量的数量积的定义及其性质,然而我们的研究

还未结束.类比向量的三种线性运算,我们还需要研究数量积的运算律及其应用,课后请大家以学习小组为单位,尝试研究向量的数量积的运算律,下节课我们一起来分享研究成果.

3 教学回顾与反思

3.1 教学回顾

本节课设计流程如图2,首先从物理模型出发,引导学生舍去事物的物理属性,抽取其中的数量关系,从而抽象出向量的数量积运算.即通过情境抽象获得对向量的数量积的最初认识:向量的数量积的运算结果是一个数量,且不仅与两个向量的大小有关,还与它们的方向有关,即向量的数量积是从a,b得到数量|a||b|cosθ的运算.这显然不能作为严格的数学定义,笔者称之为“数学相关性概念”.在“数学相关性概念”的基础上,继续引导学生垂直重组已有的数学知识(包括:零向量方向的不确定性、自由向量等)构建出新的数学结构(包括非零向量夹角,以及零向量数量积的规定),即通过理论抽象得到最终的数学概念.之后,通过一组探究题,让学生经历从特殊到一般的弱抽象过程,探究出向量的数量积的性质(可看成更高层次的数学对象).同时,得到的性质还可以反过来应用到物理模型中,如:在力和位移大小一定的情况下,随着它们夹角的增大,所做的功越来越小等.总的来说,本节课让学生经历了整个概念的生成过程,给学生足够的探究空间,这样的过程不仅有助于加深学生对于概念本质的理解,而且能够提升学生的数学抽象素养.

图2

3.2 教学反思

新课标主张数学教育应逐渐从“知识立意”转变为“素养立意”,概念教学也应将教学重心转移到培养学生发现知识的能力上面,即重视概念的抽象过程,培养学生的数学抽象素养.

(1)创设情境,引导学生抽象出数学概念

数学概念是抽象的,只有使抽象的东西获得具体事例的支持,才能加深学生对概念的理解.向量的数量积对于学生是抽象的,而物理中的求功运算却是学生熟悉的,通过求功运算引入向量的数量积,有助于学生对概念本质的理解.同时,从情境中抽象出数学概念的过程也是“用数学的眼光观察世界”的过程,这样的过程有效地培养了学生从生活中抽象出数学问题的能力.因此,在概念教学过程中,创设学生熟悉的情境,引导学生从情境出发,抽象出数学概念,既符合学生的认知发展规律,又能提升学生的数学抽象素养.

(2)重视从特殊到一般的弱抽象过程

弱抽象也叫做概念“扩张式抽象”,即从原型中选取某一特征(侧面)加以抽象,从而获得比原结构更广的结构,使原结构成为后者的特例[1].在数量积的性质的探究环节,笔者设计了从特殊到一般的弱抽象过程,首先让学生感受两个单位向量的数量积随着夹角的改变而改变,通过进一步的分析发现这样的规律适用于任意两个长度确定的向量,既而抽象出向量的数量积的一系列性质.

(3)以学生为主体,协助学生完成概念的抽象

数学活动是素养的生成和发展的培养基,数学活动的核心不是热闹的形式,而是学生的思维参与深度[2].教师在概念教学过程中,应设置以学生为主体的抽象活动,让学生经历从情境到数学概念的全过程,在活动中提升学生的数学抽象素养.在本节课中,笔者引导学生从物理模型出发,分析求功运算的特点,并抽象成数学运算,从而形成数学概念(向量的数量积),整个过程都是以学生为主体,包括数量积的定义也是由学生完成.整个过程自然流畅,充分发挥了学生的主观能动性,学生们主动思考、主动发现、相互交流并乐在其中.