强化情境创设 培养创新精神
江苏省镇江高等职业技术学校 (212016) 李 文
《普通高中数学课程标准》(2017年版)在“学业水平考试与高考命题建议”中明确指出:数学命题时,应有一定数量的应用问题,问题情境的设计应自然、合理.这里的问题情境主要是指现实情境、数学情境、科学情境等,是体现数学学科核心素养的主要方面,也能充分体现“立德树人”的教育目标.本文结合一些模拟题中对数学情境创设的不同类型的设置情况,加以实例剖析.
1 夯实基础性
以实际问题情境为数学背景载体,渗透入相应的数学基本概念与定义、公理或定理、数学公式与数学思想方法等基础性知识和能力的考查,引导学生重视数学学科的基础内容,夯实学生的数学基础知识,体现高考数学试题的基础性.
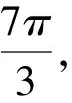
A.25-00 B.35-00 C.42-00 D.70-00
分析:根据密位制的定义,利用扇形面积公式先求出圆心角,再根据密位制的定义换算即可.
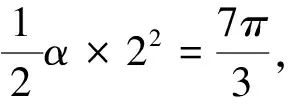
评注:通过数学情境设置,结合扇形的面积公式、任意角的三角函数的定义以及密位制的定义等,结合三角函数这一基本性数学知识来巧妙设置创新数学情境,借助相应的数学知识来分析与解决问题.
2 立足综合性
选择现实生活、生产工作中的现实案例,融入学生的现有认知水平以及数学层次,抽象概括地合理创设数学问题情境,融合数学知识与数学思想方法,综合数学多模块知识或高中多学科知识之间的交汇,考查综合知识与能力,体现高考数学试题的综合性.

A.2x1-x2=0 B.2x1-x2-1=0
C.2x1+x2+1=0 D.2x1+x2=0
分析:以数学文化为情境创设问题,结合新情景问题下的导数的几何意义以及直线的斜率公式的应用来综合应用,结合关系式的建立与化简来处理即可.

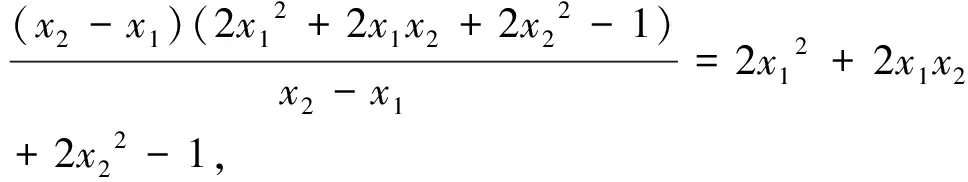
评注:通过数学文化的情境设置,巧妙综合多项式方程根与系数的关系、三次函数、函数与导数、导数的运算与几何意义、直线的斜率等众多相关知识,有机融合与交汇,实现不同知识点之间的综合性应用.
3 拓展应用性
以现实生活中实际问题作为数学问题情境,涉及工农业生产、产品制造、技术改进以及政策方案论证等,渗入开放性与探究性策略,合理引导学生独立思考和判断,打破常规思维,合理科学地作出解决问题的方案或判断,体现高考数学试题的应用性.
例3 (2023届苏锡常镇四市高三3月调研试题)天干地支纪年法源于中国,中国自古便有十天干与十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,然后地支回到“子”重新开始,即“丙子”,…,以此类推.今年是辛丑年,也是伟大、光荣、正确的中国共产党成立100周年,则中国共产党成立的那一年是( ).
A.辛酉年 B.辛戊年 C.壬酉年 D.壬戊年
分析:根据天干与地支分别构成等差数列,利用100的因式分解,结合2021年为辛丑年,进而逆推处理,分别确定100年前的天干与地支,从而得以合理判断与应用.
解析:由题意知,天干是公差为10的等差数列,地支为公差为12的等差数列,且100=10×10,100=8×12+4,因为2021年为辛丑年,则100年前的天干为“辛”,地支为“酉”,则可得到1921年为辛酉年,故选A.
评注:以中国的天干地支纪年法为问题情境创设问题,通过等差数列隐含其中,利用因式分解、逆推思维的应用来解决与之对应的应用问题.借助应用问题情境的创设,融入数学文化、中国历史、数学知识等,很好考查学生的阅读理解能力、推理论证能力等.
4 倡导创新性
选取与社会实际密切相关的数学问题情境,要求学生多角度、开放式思考问题,批判性地分析、处理与解决相应的问题,开拓思维,拓展领域,是学生创新思维和意识的加强,体现高考数学试题的创新性.
例4 (2023届徐州市高三下学期模拟题)若数列{an}对任意正整数n,有an+m=anq(其中m∈N*,q为常数,q≠0且q≠1),则称数列{an}是以m为周期,以q为周期公比的类周期性等比数列.已知类周期性等比数列{bn}的前4项为1,1,2,3,周期为4,周期公比为3,则数列{bn}前21项的和为________.
分析:结合类周期性等比数列的创新定义,确定对应参数的值以及对应的数列递推关系式,通过分组转化,结合等比数列的求和来分组求和处理.

评注:通过类周期性等比数列的创新定义,合理融合等比数列、数列求和以及创新定义等相关问题,借助创新定义加以合理分组,利用各组内的各项成等比数列,利用等比数列的公式进行分组求和处理.
在新时代背景中新高考改革下,高考数学情境创设的强化,很好开启数学教学与学习的新征程,借助创设数学试题情境,结合社会现实与生活实际,直接反映数学应用的广阔性,很好体现数学文化和数学应用的价值,以及数学的基本性、应用性与创新性.在此基础上,引导数学教学回归学生发展,回归数学本质,回归教育规律,回归实际背景,基于高中数学教材及数学基础知识,合理拓宽学生的视野,不拘泥于课本知识的约束,不断拓展学生的阅读理解能力、知识迁移能力,灵活应用数学基础知识与基本方法等“三技”来分析与解决实际应用问题,增强创新应用与创新意识,提升数学能力,有利于培养具有数学学习潜能的人才.

