结构阻尼比对超高层建筑顺风向风振响应的影响

郭小飞 ,袁哲峰 ,王 瑞,牛方义

(1.中国建筑科学研究院有限公司,北京 100013;2.建研院检测中心有限公司,北京 100013)

结构阻尼比是用来表示结构阻尼的大小,是用于结构在振动过程中能量耗散的基本术语[1]。阻尼比是超高层建筑结构风振响应分析中所要考虑的重要参数,直接决定着风荷载及风振系数的取值,进而会影响到超高层建筑结构的工程总造价。因此,论文研究阻尼比对超高层建筑结构的风振系数、基底剪力、加速度、位移等影响,为工程结构设计和规范的修正提供有效参考价值。限于篇幅,Davenport脉动风速谱对应的风荷载时程数据和工程概况参见论文《基于线性滤波法的超高层建筑脉动风速时程模拟》[2]。

1 风振系数分析方法

风荷载是高层建筑结构、高耸结构以及大跨度空间网壳结构设计时主要考虑的水平荷载之一。而在实际的抗风设计研究中,常常运用风振系数来表示。常用的风振系数分析方法有两种形式,分别为荷载风振系数和位移风振系数。荷载风振系数为结构节点的静力风荷载及脉动风荷载的总和与静力风荷载的比值;位移风振系数为结构节点的静力风荷载和脉动风荷载产生的位移总和与静力风荷载产生的位移的比值[3]。采用规范[4]给出的荷载风振系数进行研究,公式为

(1)

式中,Fk(z)为顺风向单位高度静力风荷载(kN/m),可由式(2)得出。

Fk(z)=w0μsμz(z)B

(2)

式中,Fd(z)为顺风向单位高度动力风荷载(kN/m),可由式(3)计算。

Fd(z)=m(z)(2πni)2φi(z)gσyi(z)

(3)

式中,m(z)为单位高度质量;ni为第i阶频率;φi(z)为第i阶振型;g为峰值因子;σyi(z)为第i阶振型z高度处的位移均方根。

我国规范对体型规则的建筑结构且其仅仅考虑一阶振型,风振简化计算公式为[4]

(4)

式中,ξ1为脉动增大系数;η1为脉动影响系数。

2 结构阻尼比对风振系数影响公式

结构阻尼比对建筑结构的影响作用主要体现在建筑结构的风致振动中,风振响应分析方法有频域法和时域法。在实际的工程结构设计时,为使工程师能够方便应用,我国《建筑结构荷载规范》(GB50009—2012)[4]采用等效静力风荷载来计算结构的风致响应。下面将根据第一节介绍的内容对规范给出的风振系数公式进行推导,并详细介绍阻尼比对风振系数的影响。

由式(3)可知,σq1为顺风向一阶广义位移均方根,当假设相干函数与频率没有关系时,可由式(5)计算

(5)

将风振响应近似取为准静态的背景分量及窄带共振响应分量之和。则式(5)与频率有关的积分项可近似表示为

(6)

而式(5)中与频率无关的积分项乘以φ1(z)/μz(z)后以背景分量因子表示为

(7)

将式(2)、式(3)、式(5)～式(7)代入式(1),就可以得到我国《建筑荷载规范》[3]给出的风振系数计算表达式为

(8)

式中,脉动风荷载共振分量因子R可由式(9)计算。

(9)

式中,Sf为归一化风速谱,采用Davenport教授建议的经典风速功率谱公式,则

(10)

由式(9)和式(10)就可以得到规范共振因子表达式

(11)

(12)

式中,f1为结构的第一阶自振频率(Hz);kw为地面粗糙度修正系数;ξ1为结构阻尼比。

由式(8)可以看出,阻尼比对风振系数的影响体现在共振风量因子上,并且阻尼比ξ1取值越小,风振系数公式中的共振响应因子R会越大,也就意味着风振系数βz越大,进而会导致计算风荷载越大。

3 阻尼比对风振系数的影响

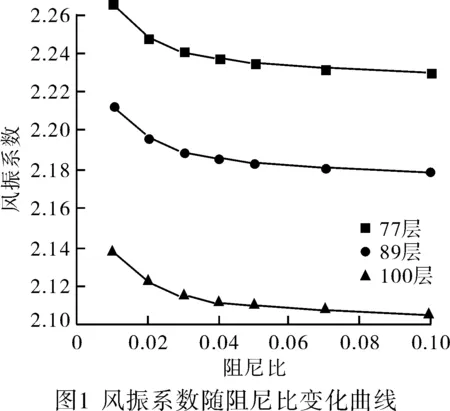
在进行超高层建筑结构风振响应分析过程中,阻尼比是一个不确定但又非常重要的因素。对于一般的钢筋混凝土结构或钢结构,阻尼比一般取值为0.01～0.05之间,为了精确地分析阻尼比对风振系数的影响,该文选择阻尼比为0.01、0.02、0.03、0.04、0.05、0.07、0.1进行分析。图1分别给出了第100层、第89层及第77层风振系数随着结构阻尼比的变化规律曲线。由此可以看出,随着阻尼比的增加荷载风振系数逐渐变小,并且变化规律渐渐趋于平缓,在结构阻尼比小于0.05时荷载风振系数缓慢变小,而在结构阻尼比大于0.05时荷载风振系数几乎无变化,这说明阻尼比较大时对结构顺风向的风振响应影响比较小。

4 阻尼比对基底剪力的影响

为了更好地了解阻尼比对建筑结构风荷载效应的影响,表1给出了不同阻尼比下结构的基底剪力最大值、平均值和均方根值。由此可以看出,整体上结构的基底剪力最大值、平均值和均方根值随着阻尼比的增大而减小,且结构基底剪力最大值随着阻尼比的增加减小幅度较大,而平均值和均方根值减小幅度较小,几乎无变化。当阻尼比从0.01增加到0.02,基底剪力最大值减小了12.69%,均方根减小了0.80%。当阻尼比由0.02增加到0.03,基底剪力最大值减小了4.96%,均方根减小了0.30%。当阻尼比由0.03增加到0.04,基底剪力最大值减小了2.77%,均方根减小了0.12%。当阻尼比由0.04增加到0.05时,基底剪力最大值减小了1.45%,均方根减小了0.06%。当阻尼比由0.05增加到0.07时,基底剪力最大值减小了2.06%,均方根减小了0.06%。当阻尼比由0.07增加到0.1时,基底剪力最大值减小了1.70%,均方根减小了0.04%。

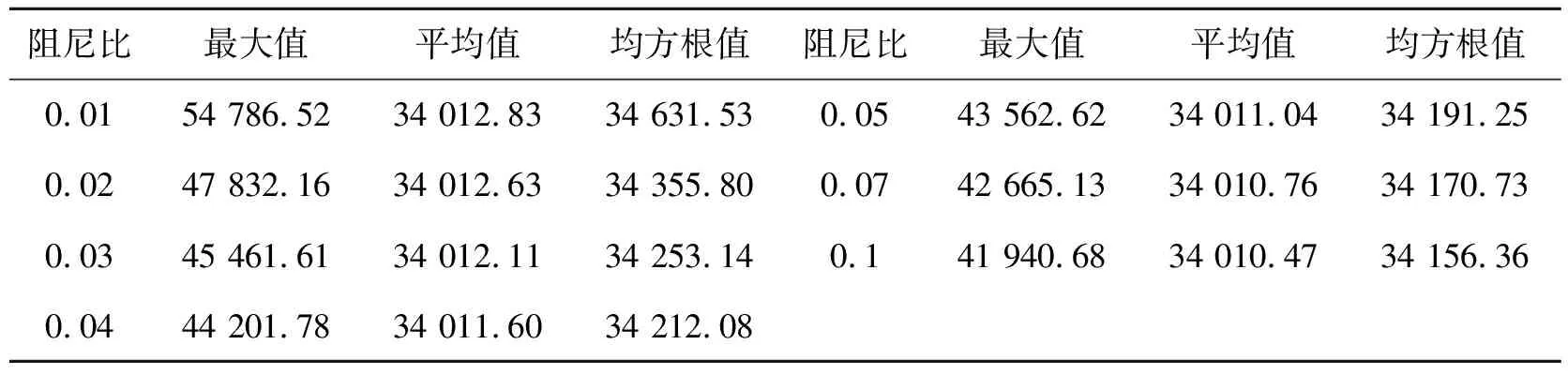
表1 不同阻尼比对基底剪力影响 /kN

5 阻尼比对位移的影响

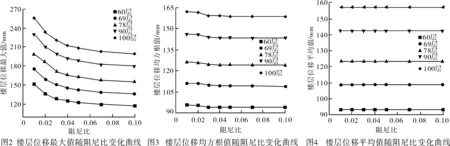
图2给出了部分楼层位移最大值随阻尼比的变化规律。图3给出了部分楼层位移均方根值随阻尼比的变化规律。图4给出了部分楼层位移平均值随阻尼比的变化规律。由图可知,60层、69层、78层、90层和100层的楼层位移最大值、均方根值和平均值随着阻尼比的变化规律基本一致,随着阻尼比的增加楼层位移最大值减小幅度较大,而均方根值和平均值减小幅度较小,几乎无太大变化,尤其是阻尼比大于0.03时。当阻尼比由0.01增加到0.02,100层的楼层位移最大值减小了8.73%,均方根值减小了0.28%。当阻尼比由0.02增加到0.03,100层的楼层位移最大值减小了5.80%,均方根值减小了1.37%。当阻尼比由0.03增加到0.04,100层的楼层位移最大值减小了3.31%,均方根值减小了0.19%。当阻尼比由0.04增加到0.05,100层的楼层位移最大值减小了2.16%,均方根值减小了0.09%。当阻尼比由0.05增加到0.07,100层的楼层位移最大值减小了2.54%,均方根值减小了0.09%。当阻尼比由0.07增加到0.1,100层的楼层位移最大值减小了1.82%,均方根值减小了0.06%。

6 阻尼比对加速度的影响

表2给出了顶层加速度最大值、最小值、平均值和均方根值随阻尼比的变化规律。由此可知,随着阻尼比的增大,顶层加速度最大值、最小值和均方根值变化量比较大,而平均值几乎无变化。当阻尼比从0.01增加到0.02,顶层加速度最大值减小了33.85%,最小值增大了33.87%,均方根减小了15.36%。当阻尼比从0.02增加到0.03,顶层加速度最大值减小了21.06%,最小值增大了22.52%,均方根减小了28.17%。当阻尼比从0.03增加到0.04,顶层加速度最大值减小了15.72%,最小值增大了16.39%,均方根减小了13.34%。当阻尼比从0.04增加到0.05,顶层加速度最大值减小了12.02%,最小值增大了12.67%,均方根减小了10.38%。当阻尼比从0.05增加到0.07,顶层加速度最大值减小了8.48%,最小值增大了16.59%,均方根减小了15.08%。当阻尼比从0.07增加到0.1,顶层加速度最大值减小了8.51%,最小值增大了13.47%,均方根减小了15.73%。

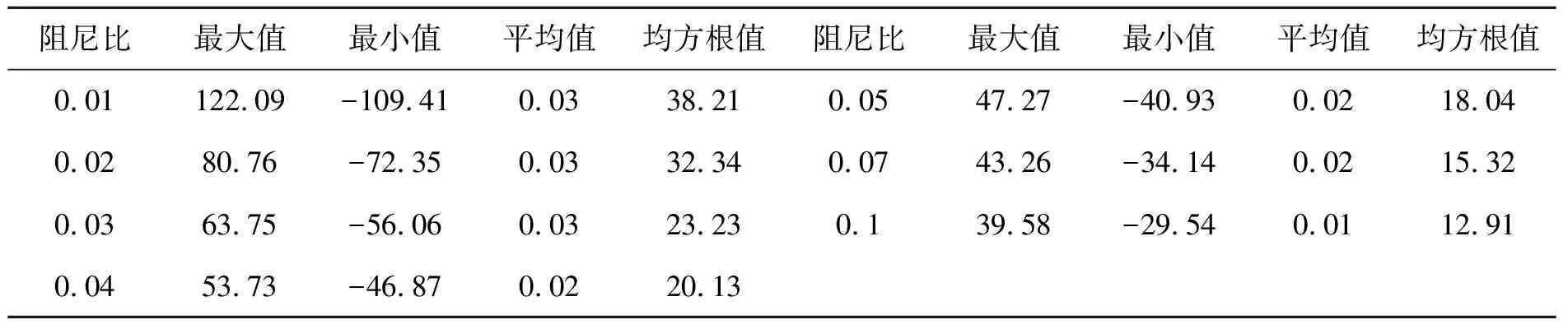
表2 阻尼比对顶层加速度的影响 /(mm·s-2)

7 结 语

阻尼比较大时对结构顺风向的风振响应影响较小。随着阻尼比的增加风振响应(基底剪力、楼层位移)最大值减小幅度较大,而均方根值和平均值减小幅度较小,几乎无太大变化。随着阻尼比的增加顶层加速度最大值、最小值和均方根值变化量比较大,而平均值几乎无变化。