多波束测线的仿真优化

夏昊 邱诗雨 单欣悦 闫雪茹

摘 要：本文针对多波束的测线方向和测线间距的问题。从相关理论入手，分析问题的几何特征，考虑测线方向的变化，推导得出海底坡面的法向量在水平面上的投影夹角β，经过数学推导，找出坡度和投影夹角的关系，给出了规则坡面下多波束测线方式模型。根据实际数据对模型进行推广，利用可视化工具建立三维海底地形图，给出不规则海底坡面下测线的最优方向和间距，从而得到一般情形下，最小化的测线总长度，证明了模型的普适性并得到局部最优解。

关键词：多波束测线；迭代优化；几何关系；仿真模拟

1 概述

为了获取更加全面精确的海底数据，覆盖范围更广的多波束测深系统已代替单波束测深成为水体测量中应用最广泛的技术之一。多波束测深系统的设计原理［1］ 是一次性发出多个独立波束，同时获得与航行方向垂直的平面内成百上千个水深值。但由于海底地形崎岖不平，数据测量难度较大，为提高海底地形的测量效率，设计简单便捷的测量方案具有重要意义［2］ 。

本文首先求出覆盖宽度W的代数表达式：

W=Dsinθ2sin（90°-θ2-α）+Dsinθ2sin（90°-θ2+α）

得出不同位置下多波束测线的重叠率。多波线测量的覆盖宽度随着海水深度的变化而减小，从而导致重叠率逐渐降低，海域最浅处的多波束测量出现严重的漏测现象，漏测率为17.42%。分析结论发现，同等条件下W会随着测线方向夹角的变化增大或减小，在水平方向时取得最大值。

2 预备知识

2.1 实验假设

（1）南北方向上海域深度无明显变化。

（2）海底地质均匀即海水深度是连续变化的。

（3）海流流速、海水温度、海内气压等其他环境因素都无明显变化。

（4）海内生物群不受声波影响，在波束发出后没有明显扰动。

（5）海底坡面平坦。

2.2 符号说明

本文用到的主要符号说明表1所示。

3 模型构建

3.1 问题分析

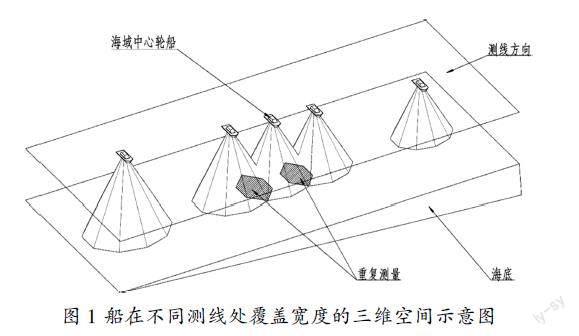
船在不同测线距中心点处的距离下覆盖宽度的三维空间示意图［3］ 如图1所示。

图1 船在不同测线处覆盖宽度的三维空间示意图

沿同一测线方向用几何画板将三维空间示意图简化为二维剖面图，如图2所示。

图2 船在不同测线距中心点处距离下的二维剖面示意图

由图2可知，在不同测线下，随着水深D的减小，多波束测深的覆盖宽度也会随之越来越小。已知条件为相邻两条测线的间距D=200M，多波束换能器的开角θ=120°，坡度α=1.5°。为更直观全面地分析此情况下各影响因素之间的联系，取距中心点处任意距离的测量点和海域中心点，通过几何模型求解出答案。

当船所在位置与测线距中心点处距离发生改变时，对应位置的水深D和覆盖宽度W也会随之变化，满足下述方程。

D=D 0 -Δh（1）

W=M i N i =M i F i +F i N i （2）

对于水深D：

在△F i F 0 H i 中，∠F i F 0 H i =α，GH=S，FH=Δh，根据正弦定理可知：

Ssin90°-α=Δhsinα（3）

Δh=S·sinαsin（90°-α）（4）

D=D 0 -S·sinαsin（90°-α）（5）

对于覆盖宽度W：

在△M i F i E i 中，∠M i E i F i =θ2，E i F i =D，根據正弦定理可知：

Dsin（90°-θ2-α）=M i F i sinθ2（6）

N i F i =Dsinθ2sin（90°-θ2+α）（7）

联立得出覆盖宽度W公式：

W=Dsinθ2sin（90°-θ2-α）+Dsinθ2sin（90°-θ2+α）（8）

化简为：

W=2sinθ（D 0 cosα-S·sinα）cosθ+2cos 2 α-1（9）

相邻条带之间的重叠率定义［4］ 为：

η=1-dW（10）

3.2 模型应用

θ为120°，s的取值为-800，-600，-400，-200，0，200，400，600，800且D 0 为70m，α为1.5°。代入公式（5）、（10）、（11）得到表2为测线距离与海水深度等因素的关系。

通过对上述结果的分析可知：

（1）在同一测线方向上，随着测线距海域中心点距离的增大，海水深度不断减小，重叠率、覆盖宽度也不断减小。

（2）同时在水深处重叠率较高，水深处会存在漏测区域。

类似地，计算得到表3展示了测线夹角与距离的关系。通过对模型和数据的分析［5］ ，可以发现以下结论。

（1）多波束擴散范围随着海拔距离的增加而扩大，在测线方向夹角在［0°，90°），测量船距海域中心点处的距离增加，覆盖宽度W通常越来越大。在测线方向夹角（90°，270°），测量船距海域中心点处的距离减小，覆盖宽度也通常越来越小。

（2）船沿等深线方向行驶即测线方向夹角β为90°或270°时覆盖宽度不发生改变。

（3）当两组数据的测线方向夹角β为360°时，覆盖宽度在任意距离上都相同。

（4）在s相同的情况下，测线方向夹角β为0°时覆盖宽度最大，β为180°时覆盖宽度最小。

基于可视化三维海底模型建立多目标的优化迭代模型，通过确定初始方向和间距创建测线，计算间距最优解和最优指标，得到结果如下。

由图3和表4可知，重叠率超过20%的区域的总长度为979.0249海里。

结语

本文在实际问题的测量中，引入测线总长度，漏测海区占比，重叠率过高部分等评价指标［6］ 全面评估测线设计的优劣。综合考虑了多角度因素，包括海底坡度，换能器开角，测线方向，模型具有很强的实用价值［7］ 。涉及多变量约束条件下的优化迭代问题，有较强的适应性。测线方向数有限，模型的精确性有待进一步检验。另一方面，实验与实际情况有所差距，可能会影响到模型的准确性。

参考文献：

［1］祝慧敏.多波束测深系统水下地形测量关键技术与精度评估［J］.经纬天地，2022（02）：46.

［2］周平.多波束测深条带拼接区误差处理方法研究［D］.东华理工大学，2018.

［3］张同伟，秦升杰，唐嘉陵等.深水多波束测深系统现状及展望［J］.测绘通报，2018（05）：8285.

［4］甘正健.提高学生使用“数形结合法”解三角函数问题的能力［J］.广西教育，2013（26）：1416.

［5］麻定很.多波束测深系统在水下地形测量中的应用研究［J］.经纬天地，2021（03）：2125.

［6］范雕，李姗姗，赵东明，等.一种海面重力数据测量精度对海底地形反演结果影响计算方法及装置：CN202111033017.3［P］.CN202111033017.3［20230922］.

［7］肖波，李善斌，管廷波，等.关于多波束测绘系统在现代海洋测绘中的应用研究［J］.中文科技期刊数据库（全文版）工程技术，2022（3）：083086.

［8］杨广义.基于多波束测深数据的海底地形建模技术及精度评估研究［D］.解放军信息工程大学，2010.

作者简介：夏昊（1996— ），男，汉族，江苏盐城人，硕士研究生，专任教师/助教，研究方向：基础数学。