基于贝叶斯网络的洪涝灾害态势预测模型

冯卓然 刘力 袁宇玲 李梦迪 罗超良

摘 要：洪涝灾害态势预测对洪涝灾害应急管理决策具有重要意义。本文基于洪涝灾害的演化规律，利用贝叶斯网络建立洪涝灾害应急决策模型，结合某地区的洪涝历史数据对洪涝灾害态势进行预测分析，为洪涝灾害应急决策管理提供科学依据。

关键词：态势预估；贝叶斯网络；Netica仿真

1 概述

洪涝灾害演化规律研究分为两个方面：监测和预测。监测包括降雨、水文数据以及利用3S技术（GIS、RS、GPS）进行的灾情监测；预测主要针对洪涝灾害发生的时间、地点和等级等。本研究基于河流水情监测信息，梳理贝叶斯网络模型结构，并确定节点间因果关系，通过EM算法计算已知信息推断未知参数的条件概率，为应急决策提供参考信息。具体而言，运用贝叶斯网络建立降水汇流模块和河道洪水模块相应的模型，研究洪涝灾害内外部相关影响因素，得到其发生和发展的规律。

2 贝叶斯网络原理

贝叶斯网络又称信念网络或有向无环图模型（Directed Acyclic Graphical Model，DAG）［1］ ，是一种基于概率图论的知识表示和推理方法，它通过构建一个有向无环图来表示变量间的依赖关系，并利用条件概率分布描述这些依赖关系。

如图1所示，贝叶斯网络中的节点分为父节点和子节点。在这个例子中，{A，B，D}是父节点，而{C，E}是子节点。接下来，我们简要介绍条件概率、贝叶斯定理和联合概率。

2.1 条件概率

条件概率是指在某个条件成立的情况下，另一事件发生的概率，用符号表示为P（B∣A），即在事件A发生的前提下，事件B发生的概率，其计算公式为：

P（B∣A）=P（AB）/P（A）.

2.2 贝叶斯定理

贝叶斯定理是以英国数学家托马斯·贝叶斯命名的一种统计推断方法。它主要用于描述两个相关事件之间的条件概率关系。给定两个事件A和B，在已知P（A）、P（B∣A）、P（B∣A）时，可以通过以下公式计算P（A∣B）：

P（A∣B）=P（B∣A）·P（A）P（B∣A）·P（A）+P（B∣A ）·P（A ）

2.3 聯合概率

联合概率是指多个事件同时发生的概率。在贝叶斯网络中，一个变量的取值依赖于其父节点的取值，可以通过条件概率来描述这种依赖关系。对于任意一组变量X 1 ，X 2 ，…，X n ，它们的联合概率分布为：

PX 1 ，X 2 ，…，X n =∏n i=1 PX i ∣X 1 ，X 2 ，…，X i-1

=∏n i=1 PX i ∣P a X i 

上式中PX 1 ，X 2 ，…，X n 为联合概率；P a X i 是X i 的父节点集发生的概率。

综上所述，贝叶斯网络通过有向无环图和条件概率表达了各个变量之间的关系，利用贝叶斯网络可以进行知识表示和推理，解决不确定性问题。

3 洪涝灾害演化参数及其数值离散化

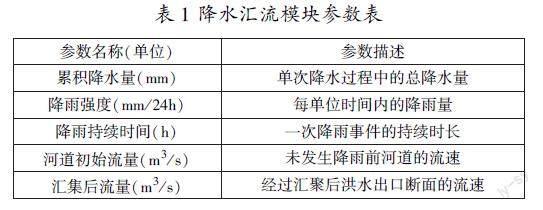
洪涝灾害演化过程中涉及大量参数且相互关系复杂。为了简化表示并降低计算难度，需要将这些参数划分为降水汇流模块和河道洪水模块两部分［1］ 。降水汇流模块参数包括累积降水量、降雨强度、降雨持续时间、河道初始流量、汇集后流量等五大参数（见表1）；河道洪水模块包括流域累积降雨量、上游实时水位、上游实时流速、下游实时水位、下游实时流速、预测洪峰到达时间等六大参数（见表2）。

此外，基于贝叶斯网络对洪涝灾害进行分析，需对所处理的参数属性进行离散化处理。接下来，我们采用等宽区间法和Kmeans法对参数属性进行离散化处理。对降水汇流模块和河道洪水模块进行离散化处理后的各变量参数分别如表3和表4所示。

4 基于贝叶斯网络的洪涝灾害演化模型

4.1 降水汇流贝叶斯网络模型

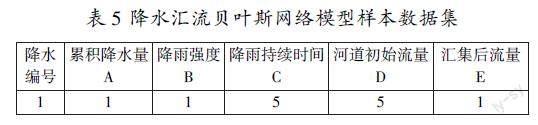
下文以某地区四年的降水汇流历史实测数据作为样本数据。首先将连续的样本数据离散化，得到200个离散化后的样本数据，如下表5所示（部分数据）。

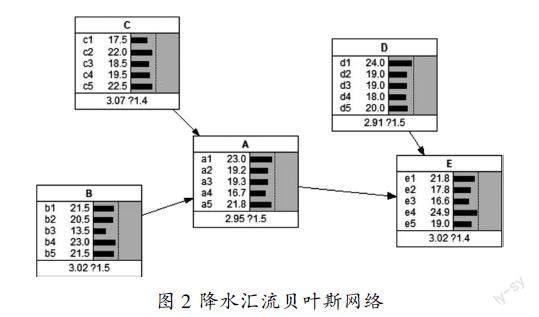
建立贝叶斯网络模型，利用Netica软件对上表样本数据集的前190个数据进行EM模型参数学习，实验结果如图2所示。

图2 降水汇流贝叶斯网络

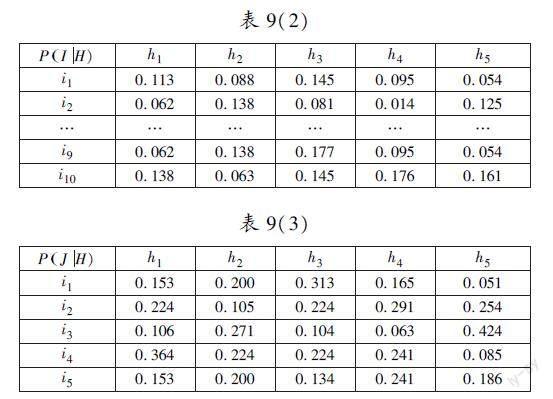
在以往的研究中，许多学者是通过直接提供条件概率表来构建贝叶斯网络模型。不过，在许多节点和复杂的因果关系场景中，直接给出条件概率变得非常具有挑战性。为了解决这个问题，我们使用Neitca软件进行模拟，实现通过数据学习自动获取贝叶斯网络的条件概率［2］ 。

对于保留的10个样本数据进行离散化处理，并把它们作为测试对比数据。根据上述降水汇流贝叶斯网络模型，计算保留样本的汇集后流量概率，最接近1的概率值代表最可能发生的汇集后流量。汇流流量节点的计算结果与真实值的对比如表7所示［1］ 。

在洪涝灾害应急决策过程中，可以将具有最大概率值视为可能发生的汇集后流量。研究发现，实测值对应的离散概率大多能达到0.88。因此，在基于概率大小评估时，该模型计算结果可为洪涝灾害应急决策提供稳定的数据支持。

4.2 洪水评估贝叶斯网络模型

接下来，以某地区河流洪水历史数据作为贝叶斯网络模型样本。首先，对连续样本数据进行离散化处理，获得200个离散化后的样本数据。

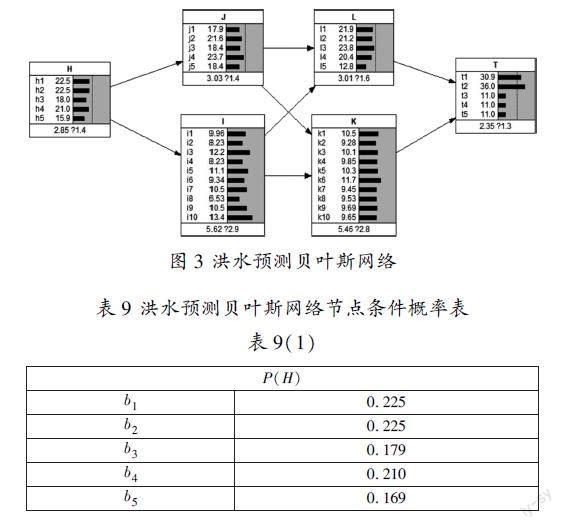
接着，利用Netica软件进行贝叶斯网络仿真。使用表8所示的样本数据集前190个数据，通过EM方法进行参数学习，结果见图3。

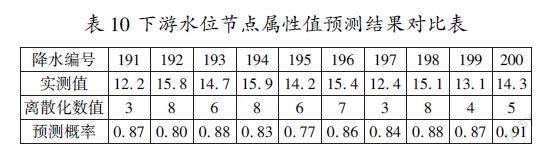
最后，对留存的10个样本数据进行离散化处理，并把它们作为测试对比数据。基于上述洪水评估贝叶斯网络模型，计算保留样本的下游水位概率，最接近1的概率值代表最可能发生的下游水位。

根据洪水评估贝叶斯网络模型对下游水位节点实际属性值评估概率大多数可达0.84，在依据概率大小进行评估时，该模型计算结果能为洪涝灾害应急决策提供可靠数据支持。

结语

本研究基于贝叶斯网络方法建立了降水汇流和洪水评估贝叶斯网络模型，对洪涝灾害演化规律及其应急决策支持进行分析研究。通过将模型计算结果与实际值进行比较分析，充分证明了所建立的贝叶斯网络模型的科学性和有效性。

参考文献：

［1］徐磊.基于贝叶斯网络的突发事件应急决策信息分析方法研究［D］.哈尔滨工业大学，2013.

［2］张一文，齐佳音，方滨兴，等.基于贝叶斯网络建模的非常规危机事件网络舆情预警研究［J］.图书情报工作，2012，56（02）：7681.

基金项目：国家级大学生创新创业训练计划项目“基于人工智能理论的城市洪涝灾害应急决策系统的设计与应用”（项目编号：202211535034）；湖南省大学生创新创业训练计划项目“基于人工智能理论的城市洪涝灾害应急决策系统的设计与应用”（项目编号：3535）

*通讯作者：罗超良（1975— ），男，湖南娄底人，博士，副教授，研究方向：随机动力系统及相关理论研究。