基于贝叶斯网络的企业财务风险研究

姚衡+王双成

【摘要】企业财务风险是指由多种因素的相互作用，使企业不能实现预期效益。目前主要采用以线性回归为基础的格兰杰方法发现企业运行指标之间的因果关系，但使用这种方法所发现的因果关系在理论和应用两方面均具有局限性。本文结合专家知识和打分—搜索方法进行贝叶斯网络学习，并将贝叶斯网络用于企业财务风险因果关系发现和分析，可为企业防范和管理财务风险提供决策支持。

【关键词】企业财务风险 因果关系 贝叶斯网络 马尔科夫毯

一、引言

贝叶斯网络（Bayesian networks）是描述随机变量之间依赖关系的图模型，由结构（有向无环图，用于定性描述变量之间的依赖和因果关系）和参数（条件概率分布表，用于定量描述变量之间的依赖和因果关系）两部分构成，具有多功能性、有效性和开放性等特征。可转化数据为知识，并利用这些知识进行推理来解决实际问题，其有效性已在许多领域得到验证。贝叶斯网络中弧的方向具有因果语义，因此，贝叶斯网络是发现因果关系和进行因果分析的有力工具，在企业财务风险因果关系研究方面具有广阔的应用前景。本文依据领域专家知识进行变量排序，结合MDL（minimal description length）标准和局部搜索方法进行贝叶斯网络学习，并将贝叶斯网络结构用于企业财务风险因果关系发现和量化影响分析。

二、贝叶斯网络

自从Pearl（1988）建立贝叶斯网络体系以来，贝叶斯网络已在许多领域得到了广泛的应用。

（一）贝叶斯网络概念

Pearl（1988）给出了贝叶斯网络的严格定义，但这一定义比较复杂，很难理解，Jensen（2001）给出的更加形象直观的贝叶斯网络描述性定义。

定义 1 把满足如下条件的有向无环图称为贝叶斯网络。

（2）每一个变量都取有限个离散值。

从贝叶斯网络的定义中可以看出，贝叶斯网络由两部分构成，分别是贝叶斯网络结构（有向无环图）和贝叶斯网络参数（条件概率分布表）。基于数据建立贝叶斯网络的核心是贝叶斯网络结构学习，现有的贝叶斯网络结构学习方法可大致分成两类，一类是基于打分—搜索的贝叶斯网络结构学习，另一类是基于依赖分析的贝叶斯网络结构学习，两者侧重的都是发现数据中所蕴含的变量之间最优因果结构，以用于因果分析和推理。

（二）贝叶斯网络学习

局部打分—搜索能够显著提高贝叶斯网络结构学习的效率，而可分解定理将为基于MDL标准的局部打分—搜索提供理论依据。

三、企业财务风险因果关系分析

企业的运行情况一般是借助指标来描述，这些指标之间存在着错综复杂的因果联系。通过建立这些指标的贝叶斯网络，能够清晰地展现指标之间的因果制约关系，再结合量化推理计算可为企业决策者提供支持。按以下程序建立企业运行指标贝叶斯网络。

（一）企业财务风险指标

选择13个企业财务风险指标，分别是：已获利息倍数（EBIT/利息费用）本期（X1），每股收益本期（X2），每股经营现金流量本期（X3），销售毛利率本期（X4），净资产收益率本期（X5），总资产净利率本期（X6），资产负债率本期（X7），本期存货周转率（X8），应收账款周转率本期（X9），总资产周转率本期（X10），总资产增长率（X11），营业总收入增长率（X12），营业利润增长率（X13）。根据所选择的13个企业财务风险指标，从万德数据库中获取2014年的上市公司企业财务风险数据。

（二）企业财务风险贝叶斯网络学习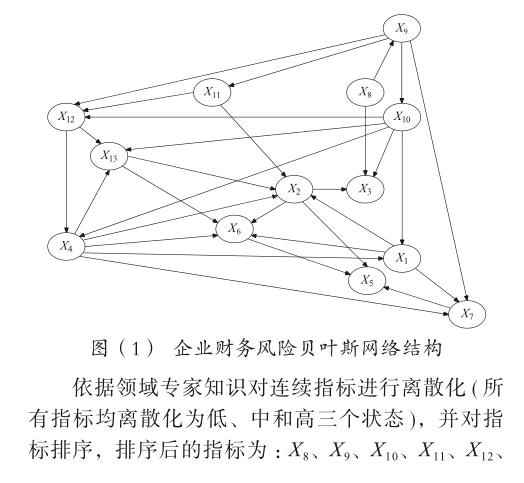

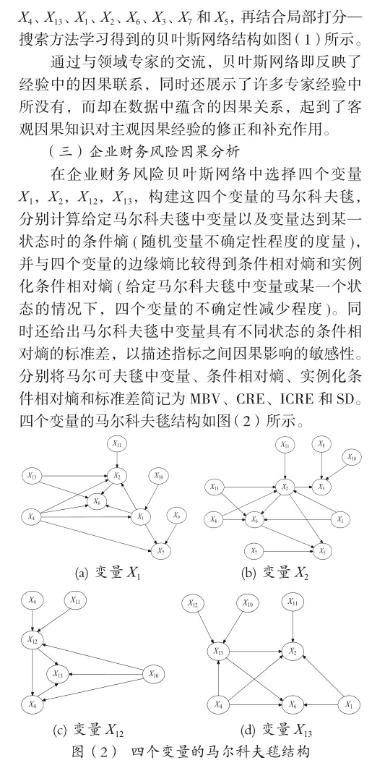
依据图（2）中的马尔科夫毯结构，对选择的四个变量的马尔科夫毯中变量对这四个变量的因果影响情况如表（1）到表（4）所示。

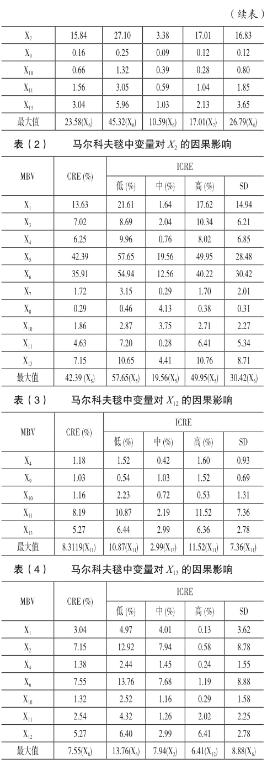
表（1）到表（4）分别给出了变量之间的量化因果影响。对X12影响最大和最小的变量是X11（不确定性降低8.19%）和X9（不确定性降低1.03%），具体状态对X12影响最大和最小的变量是X11达到状态“高”（不确定性降低45.32%）和X4达到状态“中”（不确定性降低0.42%），相对于X12最敏感的变量是X11 （标准差是7.36），最不敏感的变量是X9（标准差是0.69）。对X13影响最大和最小的变量是X6（不确定性降低7.55%）和X10（不确定性降低1.32%），具体状态对X1影响最大和最小的变量是X6达到状态“低”（不确定性降低45.32%）和X1达到状态“高”（不确定性降低0.13%），相对于X1最敏感的变量是X6（标准差是8.88），最不敏感的变量是X4（标准差是1.55）。对X1影响最大和最小的变量是X6（不确定性降低23.58%）和X9（不确定性降低0.16%），具体状态对X1影响最大和最小的变量是X6达到状态“低”（不确定性降低45.32%）和X9达到状态“中”（不确定性降低0.09%），相对于X1最敏感的变量是X6（标准差是26.79），最不敏感的变量是X9（标准差是0.12）。对X2影响最大和最小的变量是X5（不确定性降低42.39%）和X8（不确定性降低0.29%），具体状态对X2影响最大和最小的变量是X5达到状态“低”（不确定性降低57.65%）和X11达到状态“中”（不确定性降低0.28%），相对于X2最敏感的变量是X6（标准差是30.42），最不敏感的变量是X8（标准差是0.31）。这些信息将使企业管理人员进一步了解企业的运转情况，并为决策者提供有力的决策支持。

四、结语

本文在结合依据领域专家知识的变量排序、MDL标准和局部搜索的企业财务风险贝叶斯网络学习的基础上，通过不确定性推理对企业运行指标的因果影响进行了分析，可为企业经营管理人员提供人机结合的决策支持，在企业运行指标因果关系发现和分析方面具有不可替代的优势。

参考文献

[1] 王双成， 冷翠平， 李小琳. 小数据集中的贝叶斯网络结构学习[J].自动化学报， 2009 （8）： 1063-1070.

[2] 姚衡，高瑞，王双成. 基于贝叶斯网络分类器的财务信息失真识别研究[J].新会计， 2015 （6）： 37-40.注：外文参考文献（略）。