基于贝叶斯网络的城市居民出行方式研究
申健 王建锋
摘要:以西安市城市居民出行方式为研究对象,收集西安市部分区域城市居民出行的调查数据。利用获得的调查数据,综合运用相关性分析方法和K2算法进行贝叶斯网络的结构学习;应用贝叶斯参数估计方法进行贝叶斯网络的参数学习,建立了应用于西安城市居民出行方式分析的贝叶斯网络。应用所建网络分析了是否有私家车、居民性别、居民年龄和出行目的对西安城市居民出行方式的影响。研究结果表明,基于贝叶斯网络建立的西安城市居民出行方式分析模型预测精度较高,具有较高的实用价值。
关键词:交通需求管理;出行方式;贝叶斯网络;城市居民
中图分类号:TP391 文献标识码:A
1引言
随着经济的快速发展和城市规模的不断扩大,城市居民的出行需求迅速增长,但由于交通设施不足,道路通行能力提高有限,再加之机动车保有量的迅速增加,使得城市居民出行困难。公共交通是目前城市居民出行的主要方式,由于城市居民出行需求的多样性,公共交通不能完全满足城市居民的出行需求。同时由于城市居民出行方式的多样性,各种方式都有其自身的优势,因此如何使各种出行方式相互协调、合理匹配、发挥其优势,对解决城市居民出行困难、优化城市交通结构有重要的意义。
由于城市居民出行方式的复杂性,各变量之间存在大量的依赖和关联关系,因此如何建立合理的模型对其相互关联进行研究是该领域研究的热点。对城市居民出行方式研究最初采用集计方法,该方法只能表现整体的出行方式选择特性,不能表示单个出行者的出行方式,所以国内外学者开始进行非集计模型研究。McFadden在Luce和Marschak研究的基础上,对非集计模型中的典型模型Logit模型进行系统研究,建立了非集计模型的理论体系。Daniel Mefadden将效用表示为出行者出行选择因素的函数,建立了MNL模型。DanielMefadden对MNL模型不断优化,提出了混合Logit模型,该模型对出行者选择出行方式的偏好表示的更清楚。鲜于建川等选择家庭属性、出行者属性,活动一出行属性,构造了通勤出行方式选择和出行链模式安排及其相互作用的贝叶斯模型,利用敏感性分析了在出行者及其家庭的社会经济属性、活动和出行属性影响下的出行方式。唐洁等提取相关变量,利用STATA9软件分析得出家庭收入、家庭拥有车辆情况、驾照、是否高峰时段、月票、性别及退休人数与居民出行有关。本文在借鉴相关参考文献研究成果的基础上,建立城市居民出行方式分析的贝叶斯网络模型,以此模型研究西安城市居民的出行方式。
2贝叶斯网络建模方法
2.1贝叶斯网路
贝叶斯网络是基于概率推理的以贝叶斯公式为基础的图形化网络,是为了解决不定性和不完整性问题而提出的,对于解决复杂变量问不确定性和关联性问题有很大的优势,在多个领域中获得广泛应用。贝叶斯网络的构建通过贝叶斯学习实现,贝叶斯网络学习就是寻找一个能最好匹配一个给定数据训练集网络的过程。这个网络包含一个有向无环图结构和与有向无环图中每个节点相关的条件概率表,具体包括结构学习和参数学习两个步骤。结构学习是确定各个节点问的链接关系,得到贝叶斯网络结构;参数学习是确定贝叶斯网络结构中的各个节点之问的概率分布。
2.2贝叶斯网络结构学习方法
贝叶斯网络的结构学习过程是结合包含专家知识在内的先验信息,寻找与样本数据集拟合最好的网络结构。贝叶斯网络的结构学习方法可以分成三大类:基于评分搜索的方法、基于依赖分析的方法和混合方法。基于评分搜索的方法将贝叶斯网络看成是表示变量之间联合概率分布的拓扑结构,学习的目的是得到评分最优的网络结构,该方法一般首先选择网络结构的评分函数,然后通过搜索算法寻找评分最优的网络结构。基于依赖分析的结构学习方法把贝叶斯网络结构看作是编码了变量之间条件独立关系的结构,通过学习变量之间独立性关系来确定网络结构。混合方法一般先采用基于依赖分析的方法获得节点序或缩减搜索空间,然后采用基于评分搜索的方法进行贝叶斯网络的结构学习。
评分搜索法应用较多,在定义了评分函数的情况下,贝叶斯网络的学习问题就变成了一个搜索问题,通过搜索算法寻找具有最佳评分的网络结构。常用的搜索算法有K2算法,爬山法、模拟退火算法、演化算法以及抽样算法。本文采用K2算法,该算法的基本思想是:从一个空网络开始,根据事先确定的节点次序,选择使后验结构概率最大的节点作为该节点的父节点,依次遍历完所有的节点,逐步为每一个变量添加最佳父节点。在结构学习中,结构学习方法、数据等因素使学习的结果具有较大的随机性,需要经过多次实验才可能得到满意的结果。为了提高效率,贝叶斯网络的结构学习不基于实际数据,而是根据专家意见或经验确定网络结构,这样必然受主观影响,同时模型不依赖数据,模型的可移植性差。因此,为了提高网络结构的可移植性和效率,本文采用相关分析和K2算法相结合的方法。具体过程为:先进行各因素问的相关性分析,将各变量之问的相关性按大小排序,去掉与待分析变量相关性较弱的变量;再利用K2算法进行网络结构学习,不断调整变量顺序,最终确定合理的网络结构。
2.3贝叶斯网络参数学习方法
贝叶斯网络参数学习是学习变量相对于其父节点集的概率依赖程度,进而获得局部的条件概率分布函数。贝叶斯网络参数学习的基本步骤是先选择网络参数θ的先验分布p(θ),再根据贝叶斯公式(式1)计算参数的后验分布,做出对未知参数的推断。
贝叶斯网络参数学习需要综合先验信息和样本信息,通常没有先验知识来确定先验分布,针对该问题Raiffa等学者提出了选取Dirichlet分布的先验分布方法。假定参数θ的先验分布p(θ/G)为Dirichlet分布。
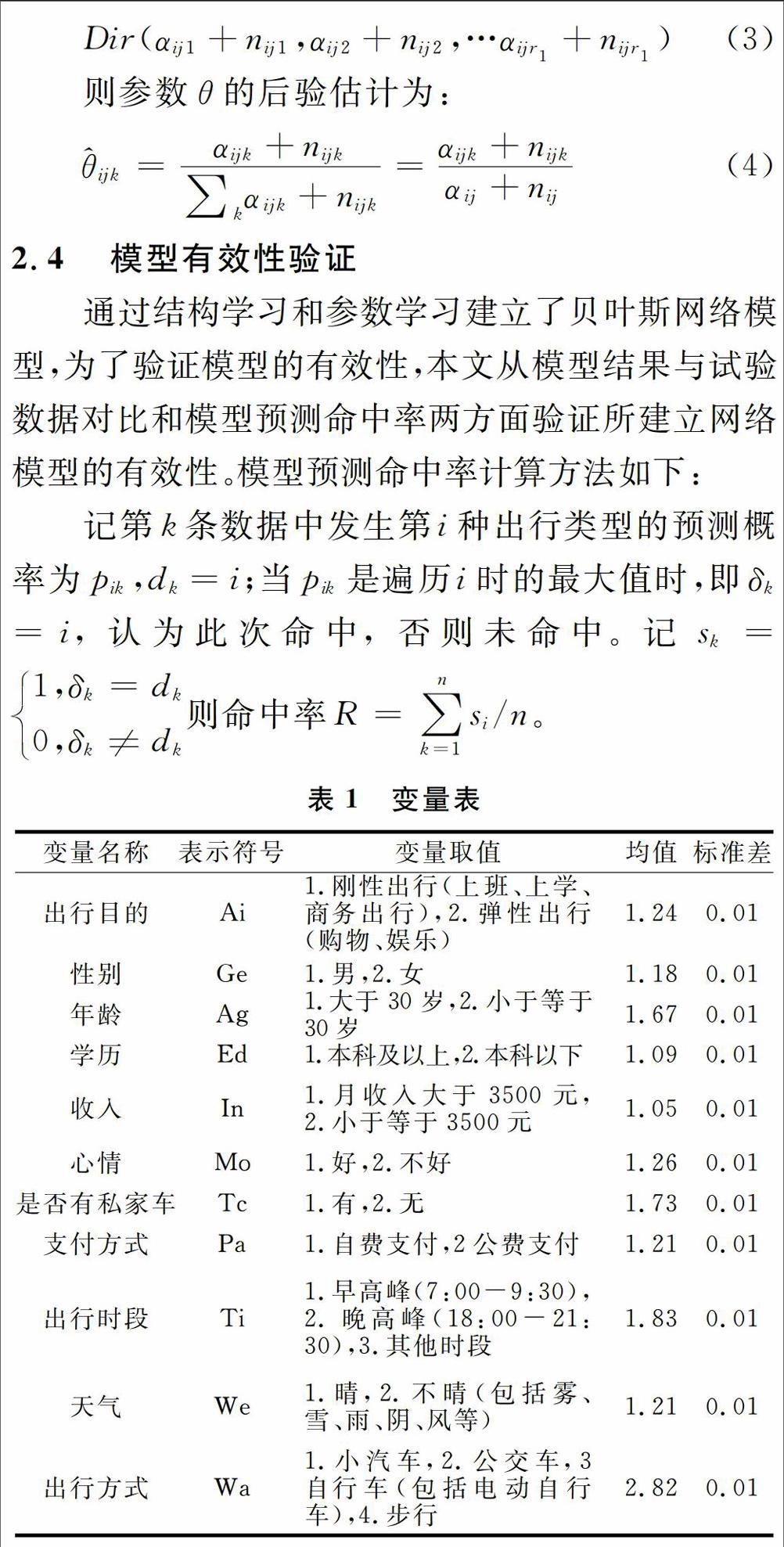
2.4模型有效性验证
通过结构学习和参数学习建立了贝叶斯网络模型,为了验证模型的有效性,本文从模型结果与试验数据对比和模型预测命中率两方面验证所建立网络模型的有效性。模型预测命中率计算方法如下:
记第k条数据中发生第i种出行类型的预测概率为pik,dk=i;当pik是遍历i时的最大值时,即δk=i,认为此次命中,否则未命中。记sk=
3西安城市居民出行方式分析的贝叶斯网络建模
3.1建模数据
本研究的数据来源于陕西省科学基金资助课题“西安市城市居民出行方式选择模糊推理研究”。在工作日和周末分别针对西安市不同的人群进行调查,地址选择在城区及近郊内的停车厂、周边小区、公共车站、大型娱乐场所、高校周边。调查方式采用问卷调查和与出行者面对面询问的方式。调查内容主要包括出行目的、年龄、性别、学历、收入、心情、是否有私家车、支付方式、出行时间等,调查者并记录当天天气情况。共计1647个有效样本。为了满足建模要求,将属性变量编码为虚拟变量,将连续变量编码为离散变量,结合相关标准和建模经验,出行方式分析的各变量设置见表1。
3.2结构学习
本研究先利用相关分析法,找出各变量之间相关性较大者,然后运用基于K2算法的结构学习方法进行西安市城市居民出行方式分析的贝叶斯网络结构学习。
3.2.1相关分析
将出行方式和出行时段作为决策变量,研究各调查变量与这两个变量之间的关系。出行方式和出行时段与各变量之问的相关分析结果见表2。
根据相关性大小,筛选出出行目的、是否有私家车、出行天气、收入、支付方式、年龄、学历、出行心情、性别、出行时段、出行方式,共计11个变量进行结构学习。
3.2.2基于K2算法的结构学习
应用Matlab工具的Full-BNF工具箱采用K2算法,进行结构学习,经过多次的变量筛选和排序调整,最终获得包括8个节点和若干联系的贝叶斯网络结构,具体结构如图1所示。网络结构图中的8个节点代表8个变量,其中包括出行时段、出行方式2个需要分析的变量。节点之问的连线表示变量之间的相互影响关系。
图1中1为支付方式,2为是否有私家车,3为天气,4为年龄,5为出行目的,6为收入,7为出行时段,8为出行方式。
3.3参数学习和模型验证
应用贝叶斯方法和Matlab的Full-BNT工具箱对建立的如图1所示的贝叶斯网络进行参数学习,在学习中将各节点的先验分布取作Dirichlet分布。在各因素的影响下,西安城市居民出行方式和出行时段2个变量的参数学习结果如下:
3.3.1出行方式参数学习结果
从图1所示的贝叶斯网络结构图可知,出行方式的父节点是出行时段,出行时段决定出行方式,即出行时段是出行方式的直接影响因素。出行方式为1(乘小汽车)、出行方式2(乘公交车)、出行方式3(乘自行车)和出行方式4(步行)的概率见表3。表3同时也给出了居民出行方式的参数学习结果和测试数据的对比情况。
分析表3中的数据可知,西安城市居民选择公交车出行方式的最高,尤其是在早高峰和晚高峰时段选择公交车出行的最高。在早高峰和晚高峰时段居民选择自行车的出行的比例也较高。在中间时段,居民选择小汽车出行、自行车出行和步行出行的比例相当。
3.3.2出行时段参数学习
从图1所示的贝叶斯网络结构图中可知,出行时段的父节点是出行目的,居民的收入和出行当天的天气。因此,西安城市居民出行目的、居民收入情况和出行当天天气与出行时段的参数学习结果和与测试数据的对比见表4。
分析表4的数据可知,西安城市居民的刚性出行主要集中在早高峰和晚高峰时段。居民的弹性出行主要集中在中间时段和早高峰前和晚高峰后,而且晚高峰后的比例更大。收入情况对居民在早高峰和晚高峰时段的刚性出行的影响不明显,但对弹性出行的影响较大。天气情况对居民早高峰和晚高峰时段的出行影响不大,但对其他时段的出行影响较大。
3.3.3模型检验
以上建立了西安城市居民出行方式分析的贝叶斯网络,并对模型的参数学习结果进行验证和对比。以下对建立的模型进行检验,以证明本文所建立的模型的有效性。对西安城市居民出行时段和出行方式两个参量的预测结果的误差值和命中率见表5。
从表5可以看出,出行时段预测模型和出行方式预测模型的预测精度都较高,出行方式预测模型的预测精度比出行时段预测模型的预测精度稍高,出行时段预测模型预测精度稍低的原因会是出行时段早高峰和晚高峰时段的精确划分较困难,同时中间时段和早高峰和晚高峰的界限也较难划分。
4模型应用
利用所建立的贝叶斯网络结构模型,计算西安城市居民是否有私家车、居民性别、居民年龄和出行目的对出行方式和出行时段的影响情况,具体计算结果见表6-表9。
从表6的计算结果可以看出有私家车和无私家车的居民选择在早高峰和晚高峰出行的比例相当。有私家车的居民选择在其他时段出行的比例大于无私家车的居民。
在出行方式方面有私家车的居民主要选择自驾车出行,无私家车的居民主要选择乘公交车出行;无私家车的居民选择自行车和步行出行的比例相当;有私家车的居民选择乘公交车出行的比例也较大。
从以上分析可知公交车出行还是西安城市居民出行的主要方式。
从表7的计算结果可以看出男性和女性居民选择不同出行时段的比例相当,早高峰和晚高峰仍是西安城市居民的主要出行时段。
在出行方式选择方面,男、女居民的比例也相当,区别是男性居民选择小汽车和公交车出行的比例略大于女性居民;男性居民选择自行车出行的比例小于女性居民,选择步行的比例高于女性居民。
从表8的计算结果可以看出大于30岁和小于30岁的居民在早高峰和晚高峰出行的比例都较高,其他时段出行的比例相对较小;大于30岁的居民晚高峰出行比例高于早高峰,小于30岁的居民早高峰的出行比例高于晚高峰。
大于30岁的居民和小于30岁的居民选择公交车出行的比例相当且比其他出行方式高,这说明公交车是西安城市居民出行的主要方式。大于30岁的居民选择小汽车出行的比例高于小于30岁的居民。
可以得到,西安年轻居民主要选择公交车和自行车出行,中年以上居民主要选择公交车出行和步行。
从表9的计算结果可以看出居民刚性出行主要集中在早高峰和晚高峰,弹性出行主要集中在晚高峰和其他时段。西安城市居民刚性和弹性出行的方式主要是小汽车和公交车,但弹性出行选择小汽车的比例高于刚性出行。
5结束语
本文应用贝叶斯方法,研究西安城市居民出行方式。建立了西安城市居民出行方式和出行时段的贝叶斯网络模型。利用所建立的模型研究了是否有私家车、居民性别、居民年龄和出行目的对出行方式和出行时段选择的影响。所建立的贝叶斯网络模型对深入研究西安城市居民出行方式和出行时段的影响因素,对西安的交通规划发展有一定指导意义。