基于改进粒子群算法的PID控制参数优化*

黄训爱,杨光永,樊康生,陈旭东,徐天奇

(云南民族大学电气信息工程学院,昆明 650500)

0 引言

PID控制结构简单,适应性强,操作方便,被广泛应用在工业过程控制领域[1]。PID控制器的参数整定结果直接影响着PID控制器性能,通过人工经验方法调整参数比较耗时,且很难达到控制要求。因此,选取合适的方法对PID控制器参数进行整定显得尤为重要。最早的PID参数整定方法由Ziegler和Nichols提出(简称Z-N法)[2]。随着现代生产自动化程度的提高,系统复杂性,非线性特性以及被控对象不确定性日益突出,传统的Z-N法不再满足要求。

近年来,群智能技术发展迅速,并广泛应用在各个领域,如粒子群算法[3]、遗传算法[4]、海鸥优化算法[5]、麻雀搜索算法[6]等。随着群智能技术的发展,越来越多的智能优化算法广泛应用于PID控制参数优化,如宋娟等[7]提出基于果蝇优化算法优化PID参数,但算法后期搜索速度慢且易陷入局部最优;赵广元等[8]提出改进的人群搜索算法,响应速度较快但控制精度较差;李远梅等[9]提出一种变步长的萤火虫算法优化PID参数,但算法收敛速度较慢;王正等[10]提出一种改进花授粉算法,算法收敛精度低,局部搜索能力较弱;边莉等[11]提出蚁狮优化算法,算法虽精度高,更容易找到群居最优解,但系统响应速度很慢;WANG等[12]提出基于神经网络的PID参数优化,但算法计算量较大;张继荣等[13]提出改进粒子群优化算法,惯性权重系数呈非线性变化,能够避免算法后期陷入局部最优,但收敛速度较慢;HONG等[14]提出遗传算法优化隧道火灾烟气控制PID通风系统的参数优化与确定,并与解析试错法进行对比。

针对各种智能算法优化PID控制器参数存在的问题,本文提出一种融合中垂线策略的改进粒子群优化算法(MAPSO)。首先基于中垂线策略的游离粒子位置更新方法,能够加快粒子的收敛速度,从而增强算法的寻优速度和寻优精度;同时引入惯性权重余弦调整方法,解决算法迭代后期易陷入局部最优问题。采用6种测试函数对其性能进行测试,相比其他改进粒子群算法,本文算法不仅收敛速度快,且算法收敛精度和稳定性相比其他算法具有很大优势。将MAPSO应用于PID控制器参数优化,并与Z-N法、均值粒子群优化算法进行对比,仿真结果表明该算法在PID控制器参数优化中相比其他两种算法具有更大优势。

1 MAPSO算法优化PID控制器原理

MAPSO算法优化PID控制器原理是在保证整个系统稳定的前提下,选取合适的KP、Ki、Kd(KP、Ki、Kd分别表示比例、积分和微分项系数),使控制系统的控制性能达到最佳。

图1为MAPSO优化PID控制器原理图,首先PID控制器对被控对象进行控制,计算出一组初始KP、Ki、Kd参数,然后系统把3个参数分别传递给MAPSO算法进行优化,根据性能指标评价函数作为适应度函数进行计算,找出种群中的全局最优值并依次赋值给Kp、Ki、Kd,判断是否满足终止条件,直到找到最优参数。

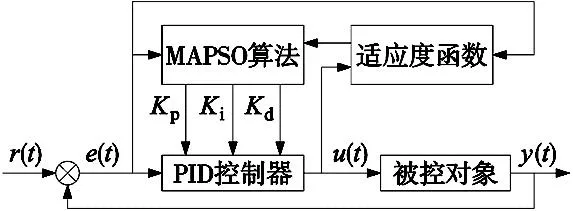
图1 MAPSO优化PID控制器原理图

2 融合中垂线策略的改进粒子群算法

2.1 速度和位置更新策略

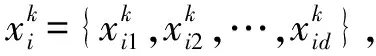
(1)

第k次迭代时粒子到达的全局最佳位置为:

(2)

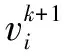
(3)

(4)

式中:w为粒子运动惯性权重系数,其大小影响局部和全局寻优能力;c1和c2为粒子学习因子,一般取值c1=c2=2;r1和r2是(0,1)之间服从均匀分布的随机数。

2.2 中垂线策略原理

本文结合文献[3]中垂线原理提出中垂线算法(MA)收敛策略,一条线段的中垂线上任一点到这条线段两端的距离相等,粒子根据这一几何性质,不断缩小最优解的搜索范围从而找到最优解。如图2所示,假设在一个二维空间内,在矩形围成的范围内(如图中阴影区域所示)仅存在一个最优点P,存在随机的两个点A和B,将两点连接起来形成一条线段AB,作线段L为AB的中垂线,定义|PA|<|PB|,则P点必存在于线段L靠A侧区域。中垂线算法把最优点到P点的距离用其适应度值来代替,因AP的距离小于BP的距离,即A点适应度比B点更优。P点具有最佳适应度,如图2所示,中垂线算法收敛过程为:

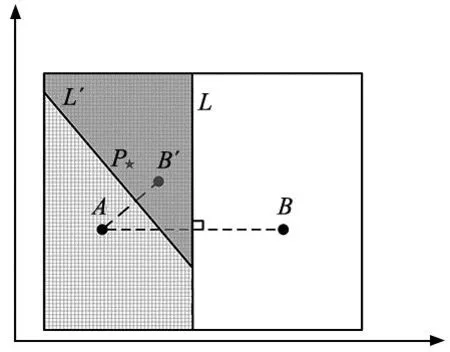
图2 中垂线算法原理图

(1)判定|PA|是否小于|PB|,若是,则判定最优值位于中垂线靠A侧区域内(图1网格区域);

(2)丢弃B点,在中垂线L靠A侧区域重新随机生成一点B′;

(3)A点和B′点构成线段AB′,作其中垂线L′,此时B′点离P点更近,即B′点适应度更好,则MA判定最优值位于L′靠近B′点区域内(图1阴影区域);

(4)重复上述步骤不断生成新的A点,通过MA方法即可不段缩小最优点所处空间。

2.3 融合中垂线算法的粒子位置变化策略

在图2中加入一个随机粒子C,并且C位于L靠A侧区域,如图3所示,若采用传统PSO的粒子位置更新策略更新B点和C点位置,要经过多次迭代才能到达中垂线靠A侧区域。

图3 改进算法原理图

如图3所示,将粒子B和C移动到B′点和C′点上,再采用PSO的粒子速度和位置更新策略,可以加快PSO的速度和位置更新。上述策略实现方式为:首先判断粒子是否位于中垂线靠B侧区域,设:

(5)

若粒子x在线段L靠B侧区域,则x的第j维变量满足下式:

(6)

式中:

(7)

为了减小算法的时间复杂度和全局寻优能力,判定x仅需有两维变量不符合上述策略,则粒子位于A侧区域,粒子位置更新不采用上述策略。

若MA判定,若粒子位于中垂线靠B侧区域,则B点更新公式为:

(8)

(9)

2.4 惯性权重系数选择策略

PSO算法优化策略中惯性权重系数w影响算法的收敛速度和收敛精度,选择合适的w至关重要。标准PSO算法惯性权重系数按迭代次数的增加依次线性减小,其变化过程按式(10)进行更新:

w(k)=wmax+w(wmin-wmax)(k/kmax)

(10)

式中:k为当前迭代次数,w(k)为第k次迭代权值,kmax为最大迭代次数,wmax为最大权值,wmin为最小权值。

标准PSO算法中的惯性权重系数是一个固定值,在全局搜索时不能很好的逼近全局最优值。因此,本文选取文献[13]中的余弦调整惯性权重的策略,在w的迭代过程中引入随机函数rand,并引入余弦变化,使惯性权重动态变化,避免算法迭代后期陷入局部最优,其公式为:

w(k)=randwmin*(1-cosh)+wmax*cosh

(11)

式中:h=πt/2kmax,wmax=0.9,wmin=0.4。

3 算法性能验证

3.1 测试函数设定

本文通过选取6个基准测试函数测试改进算法性能,其中F1～F3为单峰函数,F4～F6为多峰函数。基准测试函数如表1所示。采用基于自适应策略的改进粒子群优化算法(MPSO)、均值粒子群优化算法(MeanPSO)与本文的中垂线粒子群算法进行对比,测试函数维度为30,实验平台为MATLAB2019b(Intel(R)Core(TM)i5-8250UCPU@1.60 GHz)。

表1 基准测试函数

3.2 参数设置

针对本文的改进算法和其他两个算法作对比进行性能验证,各算法参数设置为:

自适应策略的改进粒子群优化算法(MPSO):种群规模80,迭代次数200,重复试验次数50,学习因子c1=c2=2,惯性权重系数最大值wmax=0.9,最小值wmin=0.4。

均值粒子群优化算法(MeanPSO):种群规模80,迭代次数200,重复试验次数50,学习因子c1=c2=2,惯性权重系数w。

中垂线粒子群算法(MAPSO):种群规模80,迭代次数200,重复试验次数50,学习因子c1=c2=2,惯性权重系数wmax=0.9,最小值wmin=0.4。

本文计算的标准差和平均值分别用来评价算法稳定性和收敛精度;因数据矩阵随机产生,每次独立试验结果不一定为最优值,故本文重复试验50次取其平均值,结果如表2所示。

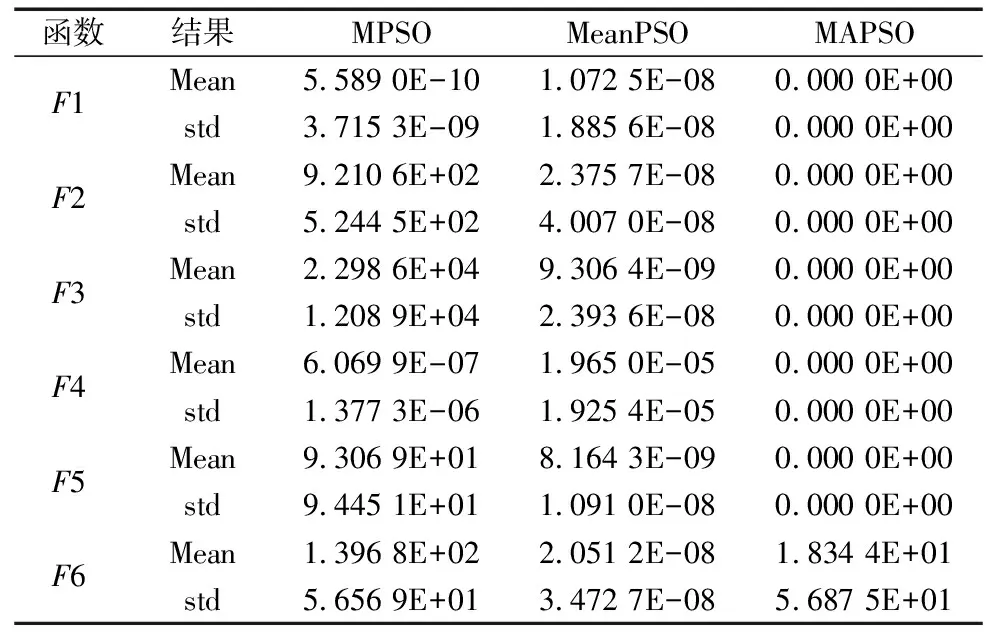
表2 均值与标准差实验结果

3.3 各算法性能对比实验分析

进行对比实验时,规定各测试函数维度为30维,独立实验次数为50次。

(1)算法收敛精度分析:3种改进粒子群算法中,当测试函数为F1～F5时,MAPSO算法的均值是最小的,略大于MPSO,但小于MeanPSO的均值。实验数据表明在处理单极值问题时,MAPSO收敛精度在3种算法中是最好的,在处理多极值问题时,算法同样表现良好。

(2)算法稳定性分析:MAPSO实验结果的标准差同样在测试函数为F1～F5时最小,在测试函数为F6时略大于MeanPSO和MPSO,实验数据表明MAPSO在处理单极值问题时稳定性极佳,处理多极值问题时均也不弱于MeanPSO和MPSO。

(3)算法收敛速度分析:图4为适应度值变化曲线。从图中可以看出,当测试函数为F1、F2、F4、F5、F6时,MAPSO算法的收敛速度明显快于其他两种算法,当测试函数为F3时,MAPSO算法收敛速度与MeanPSO算法基本相同,且明显优于MPSO算法,说明本文改进的算法具有较快的收敛速度。

(a) 各算法处理F1时收敛曲线 (b) 各算法处理F2时收敛曲线

4 基于MAPSO的PID参数整定

4.1 性能指标函数选取

PID参数的整定,就是为了选取合适的KP、Ki、Kd值,然后通过性能指标判断PID各参数是否达到最优,因此选取合适的性能指标尤为重要。常见的性能指标评价公式为:

(12)

(13)

(14)

(15)

由于初始时刻的偏差最大,使用ISE公式会使误差平方项在瞬态过程中起主导作用,稳态过程的作用较小,造成较大的超调和较大的误差;ITSE相比ISE增加了时间因素,系统响应变快稳态误差变小,但效果不是很明显;IAE虽然设计简单,但仅考虑误差的大小,系统响应较慢,而ITAE相比IAE考虑了时间的因素,系统响应素的和稳态性能均有很大提升,综合考虑本文选取ITAE作为性能指标函数。

4.2 MAPSO算法优化步骤

具体优化步骤为:

步骤1:初始化MAPSO算法的种群规模、速度、惯性权重系数等一系列参数;

步骤2:将种群个体解码为KP、Ki、Kd;

步骤3:运行simulink模型,选取ITAE性能指标作为适应度函数;

步骤4:更新当前个体最优位置和群体最优位置,并与粒子个体最优适应度值和群体最优适应度值做比较,如果当前值较优,则保存该位置;

步骤5:根据惯性权重余弦调整公式计算惯性权重值,对适应度值进行排序;

步骤6:根据式(3)、式(4)更新粒子速度和位置;

步骤7:通过sim函数调用搭建的simulink模型,并返回新一代种群的适应度函数值,与步骤4进行比较,更新位置;

步骤8:判断是否达到最大迭代次数,若达到则迭代结束,否则返回步骤2。

4.3 实验仿真

由于大部分实际控制工程都是复杂的高阶系统,所以本文选取的被控对象传递函数为高阶不稳定系统如式(16)所示。

(16)

将Z-N公式法、MeanPSO算法与本文的MAPSO算法分别应用到PID的参数整定中,并对实验结果进行对比。

MAPSO算法参数设置如下:粒子群规模80,迭代次数为100,学习因子c1=c2=2,惯性权重系数wmax=0.9,最小值wmin=0.4。粒子速度vmax=1,vmin=-1,Kp、Ki、Kd三个参数的取值范围为[0 300]。

MeanPSO算法参数设置如下:粒子群规模80,迭代次数为100,学习因子c1=c2=2,惯性权重系数w=0.9。粒子速度vmax=1,vmin=-1,Kp、Ki、Kd三个参数取值范围为[0 300]。

4.4 实验结果及分析

在ITAE性能指标下,MeanPSO算法和MAPSO算法优化PID控制器参数性能指标的最优个体适应度值收敛曲线如图5所示。

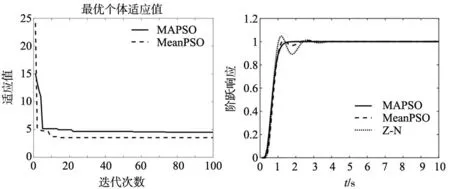
图5 适应度函数收敛曲线

由图5可以看出MAPS0算法在迭代10次左右便开始收敛,收敛精度高且稳定性好,而MeanPSO在迭代5次左右即有陷入局部最优的趋势,在迭代25次左右才趋于稳定,表明MAPSO收敛速度和收敛精度明显优于MeanPSO。

3种算法最终得到的PID参数整定结果如表3所示,阶跃响应曲线如图6所示。

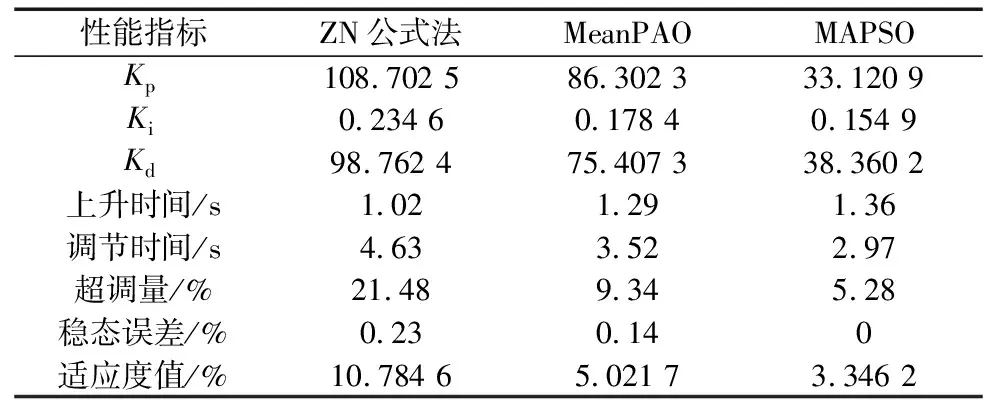
表3 PID参数整定结果

从实验数据可以看出,Z-N公式法虽然响应速度快,但在调节时间和超调量上性能最差。MAPSO算法与MeanPSO算法相比较,超调量、响应速度和稳态误差等性能指标都优于MeanPSO所得结果。证明在ITAE性能指标下,MAPSO对PID参数的整定具有较好的效果。

5 结论

本文对传统粒子群算法进行改进,提出一种融合中垂线策略的中垂线算法,增强算法的寻优速度和寻优精度;并引入惯性权重余弦调整的方法,避免算法陷入局部最优。选取6个测试函数对MAPSO算法进行测试,实验数据表明该算法的收敛精度和收敛速度均优于其他两种改进粒子群算法。将该算法应用到PID的参数整定中,在仿真环境下,与Z-N公式法和MeanPSO算法进行对比实验,证明该算法得到的性能指标更好。