面向真实世界的测试函数Ⅱ

彭复明

(南京工业职业技术学院 计算机与软件学院，江苏 南京 210046)

引言

多年来，人们一直使用传统函数作为无约束优化的测试函数。这些函数有一个共同特点，就是全局最优解是已知的。也就是说，让算法去寻找一个已知具体方位的全局最优解，这在现实世界中是荒唐的。如果某算法声称已找到了测试函数全局最优解，别人如何判别它的真实性呢?要想得到正确的答案，只有重现算法程序并运行。然而，重现别人的算法并不是一项轻松的工作。为了解决这一问题，本文构造了面向真实世界的测试函数，它的全局最优解有可能为零或从正向接近零，但全局最优解坐标却是未知的。如果某算法找到了此类测试函数值为零的具体坐标，那么说这个算法找到了该测试函数的全局最优解就确信无疑了。

1 传统测试函数的弊端

下面就举几个典型传统测试函数的例子，说明它们不能检测出算法的真实水平［1］。

(1)sphere函数

(3)Rosenbrock函数

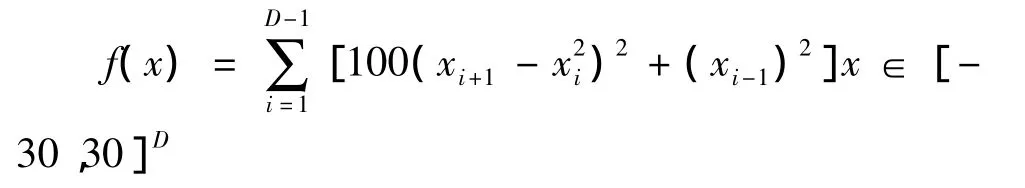
其中，D表示维数。

sphere函数与Rastrigin函数的最优解坐标在原点(0，0，…，0)，Rosenbrock 函数的最优解坐标为(1，1，…，1)。

现在对于函数(1)、(2)，设计算子S1如下:

Xk+1=0.5Xk

式中:X0:初值，k:进化代数。

只要S1算子运行1000多代，就一定收敛到全局最优解。

对于函数(3)，当进化计算到一定代数后，有一些优良个体出现优良分量(1或接近1)。采用如下策略可以使算法快速收敛到全局最优解。

假如有优良个体A(‥，Xi，‥，Xj，‥)，(Xi，Xj为优良分量)制作多个 A的副本 B(‥，Xm，‥，Xn，‥)。然后，进行以下操作:

式中:i、j、m、n 是满足 i≠m，j≠n 的随机整数。

在算子S2的作用下，B的优良分量有可能比A多，它在竞争中被保留下来。如此这般，所有分量都是优良分量的个体很快就会出现。

算子S1优化全局最优解设在原点的测试函数能够较快收敛，但对于全局最优解不在原点的测试函数就无能为力了。算子S2优化全局最优解的各个坐标分量完全相同的测试函数能够获得优异的测试性能，可在现实的世界中，不太可能会有这样的优化函数。所以说，算子S1、S2对三个传统测试函数的测试性能优良并不能说明对现实优化问题就会有良好的效果。由此可以推断，此类传统测试函数不能测试出算法的实际水平。

另外，还有一类测试函数［2］，它对传统测试函数作了改进，将测试函数的全局最优解坐标进行随机设置，全局最优解坐标各分量之间没有丝毫关联。但它也有致命的弱点，就是全局最优解对算法来说是已知的［3-4］。人们同样可以设计算子，随机抽取部分或全部全局最优解坐标，把它加入到进化过程中，使算子快速收敛到全局最优解，这样的算子同样经不起现实世界中优化问题的考验。

综上所述，目前迫切需要能够检测出算法真实水平的测试函数。一个好的测试函数不应该给算法任何不当的机会找到全局最优解。按照这个原则，下面推出面向真实世界的测试函数。

2 面向真实世界的测试函数

2.1 基本测试函数

构造基本测试函数的原则是永远不让人找到它的全局最优解［5］。这里一共创建了5个函数，下面就是这些函数的具体描述。

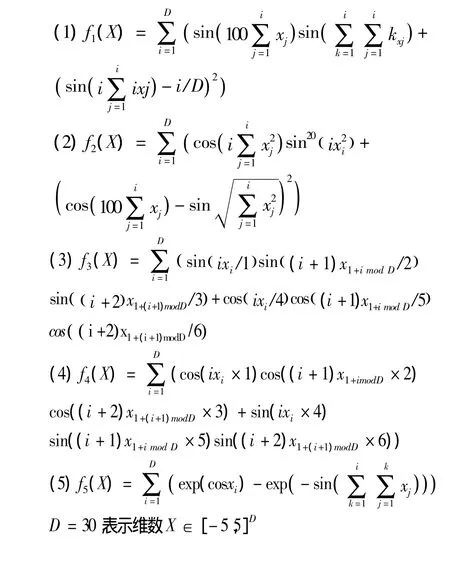
2.2 发展测试函数

在基本测试函数的基础上构建了6个发展测试函数(简称发展函数，用 DF(X)表示)。构建 DF(X)有三个要求。1)DF(X)≥0。2)DF(X)的全局最优解尽可能设置为零。3)DF(X)的全局最优解的坐标是未知的。下面是发展函数的具体描述。

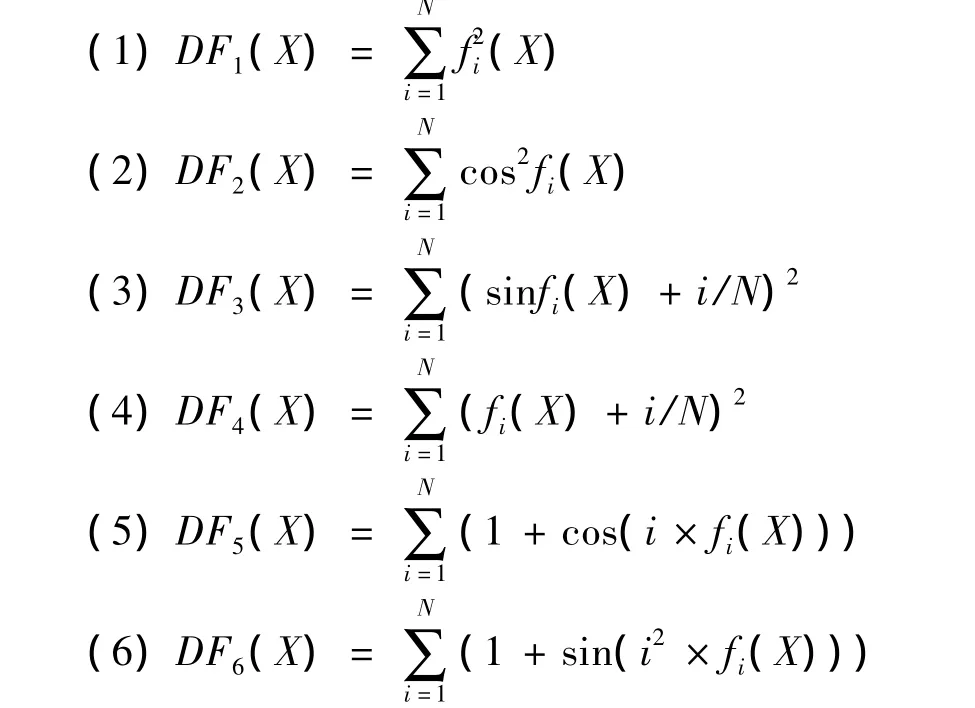
式中:N=5，表示基本测试函数的个数，X∈［－ 5，5］D。

3 实验数据与分析

本文作者使用了协同进化数值优化算法(Coevolutionary Algorithm for Numerical Optimization，简称CANO)对6个发展函数进行数值优化。具体的最优解数据见表1，表2、表3是CANO算法对DF5(X)、DF6(X)进行数值优化的最优解坐标，其他4个函数的最优解坐标公布在相关网站上。

从表1可以看出，已有DF5(X)、DF6(X)的最优解达到零，说明算法已找到了DF5(X)、DF6(X)的全局最优解。其他4个发展函数的最优解也都非常接近零。在没有找到使DF(X0)=0的X0坐标之前，谁也不敢断言DF(X)的全局最优解为零。所以说，DF1-4(X)的全局最优解是否为零还不得而知。

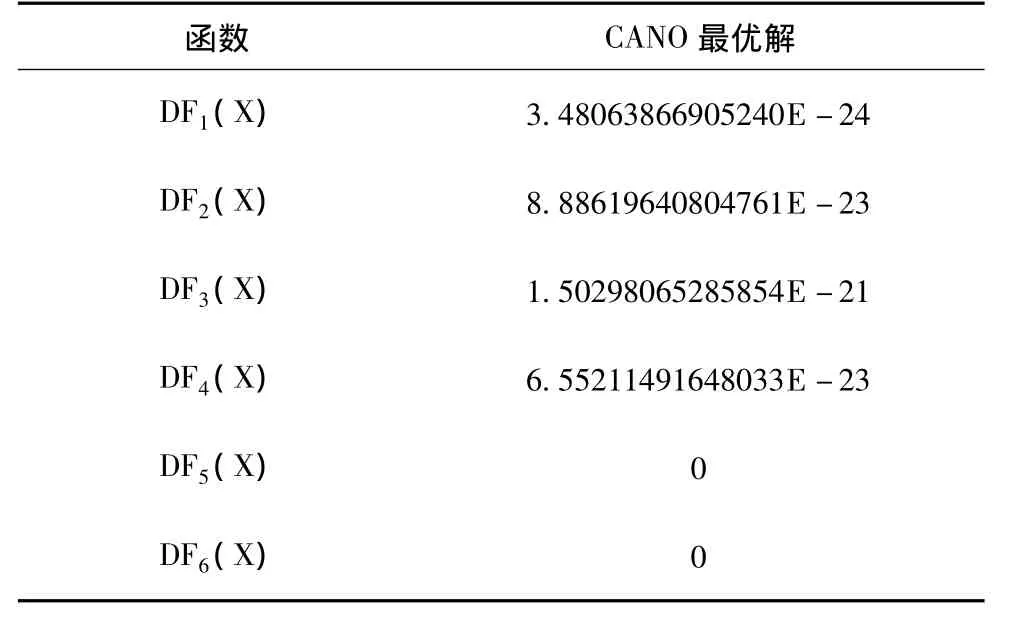
表1 CANO优化发展函数的最优解

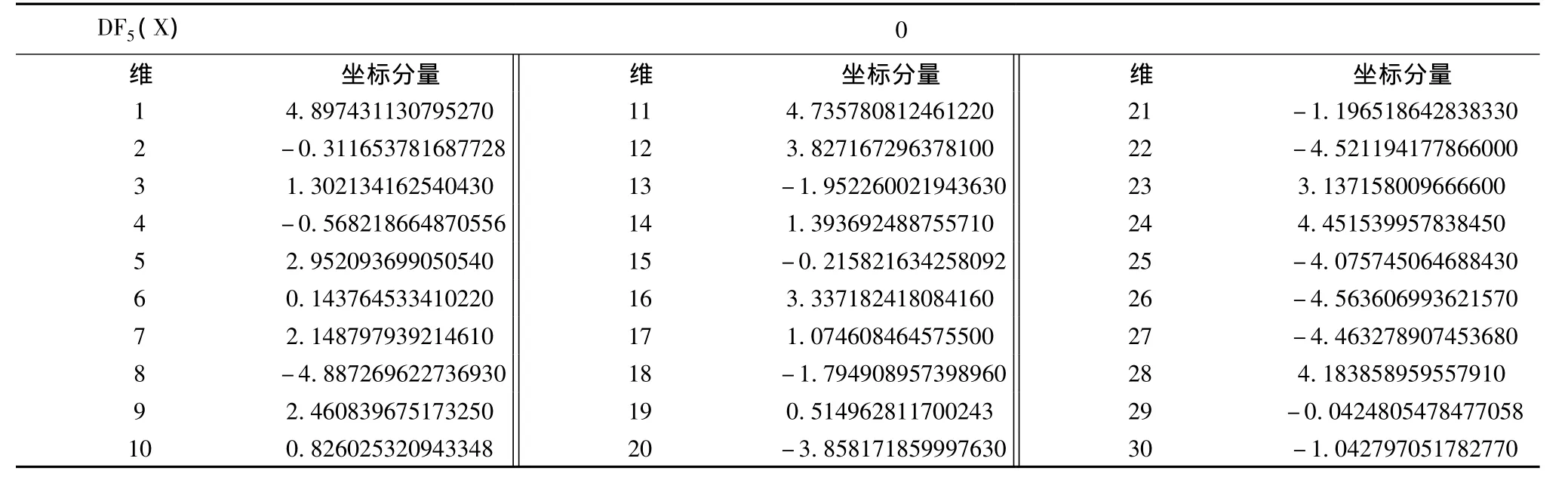
表2 CANO算法对DF5(X)进行数值优化的最优解坐标

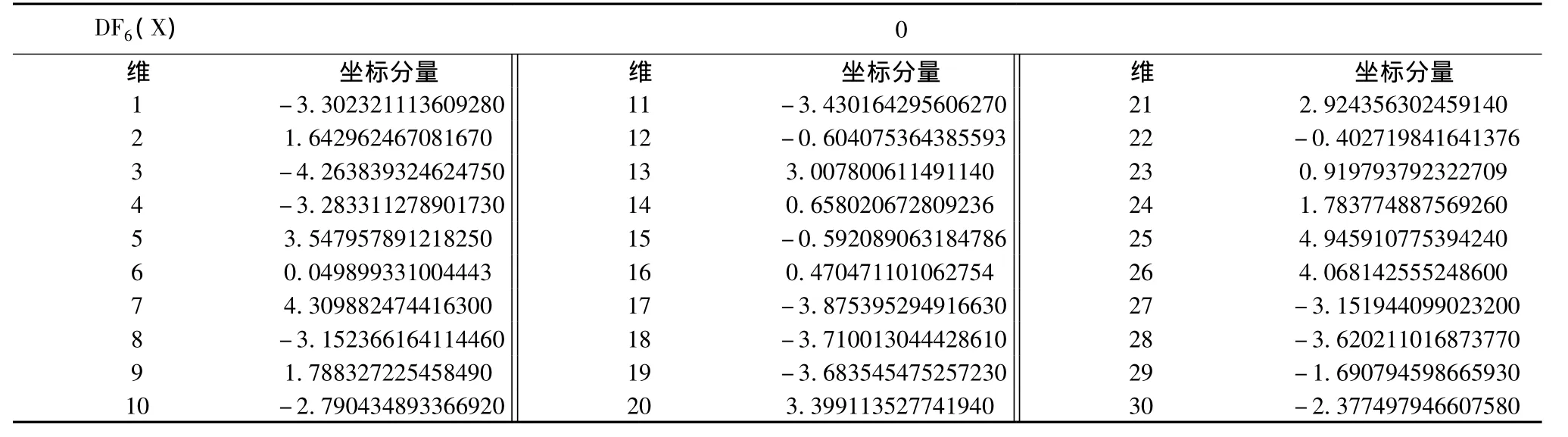
表3 CANO算法对DF6(X)进行数值优化的最优解坐标

4 结束语

由于传统测试函数的全局最优解坐标是已知的，所以它不能完完全全地检测出算法的真实水平［6］。面向真实世界的测试函数很好地隐藏了全局最优解坐标，算法只能凭借自身实力搜索全局最优解。所以，它能检测出算法的真正水平。面向真实世界的测试函数系统要求算法研究者在http://testfunctions.niit.edu.cn/网站上输入最优解坐标。这样，算法优化测试函数最优解的各项数据就自动产生了。这些数据可以看作第三方的认证，提供给杂志社与审稿专家，作为算法优劣的有力证据。

［1］ YAO Xin，LIU Yong，LIN Guang-ming.Evolutionary Programming Made Faster［J］.IEEE Transactions on Evolutionary Computation，1999，3(2):82-102.

［2］ LIANG J J，SUGANTHAN P N，DEB K.Novel Composition Test Functions for Numerical Global Optimization［M］//Proceedings of IEEE International Swarm Intelligence Symposium.Italy:Messina，2005:68-75.

［3］ TANG Ke，LI Xiao-dong，SUGANTHAN P N，YANG Zhenyu，WEISE Thomas.Benchmark Functions for the CEC'2010 Special Session and Competition on Large-Scale Global Optimization［EB/OL］.［2014-2-25］.http://www.researchgate.net/publication/228932005_Benchmark_functions_for_the_CEC%272008_special_session_and_competition_on_large_scale_global_optimization.

［4］ TANG Ke，LI Xiao-dong，SUGANTHAN P N，YANG Zhenyu，WEISE Thomas.Benchmark Functions for the CEC'2008 Special Session and Competition on Large Scale Global Optimization［EB/OL］.［2014-2-25］.http://www.researchgate.net/publication/228932005_Benchmark_functions_for_the_CEC%272008_special_session_and_competition_on_large_scale_global_optimization

［5］ PENG Fu-ming.Real World Oriented Test Functions［M］//The Proceedings of 2011 International Conference on Computer Science and Service System.2011，2:1499-1505.

［6］ PENG Fu-ming.Novel Composition Test Functions Algorithm for Numerical Optimization M］//The Proceedings of 2011 International Conference on Computer Science and Service System.2011，4:3348-3352.