融合改进哈里斯鹰和改进动态窗口的机器人动态路径规划

黄志锋 刘媛华 任志豪 张文敏 张孝文

收稿日期：2023-06-12；修回日期：2023-08-07  基金项目：国家自然科学基金资助项目（72071130）

作者简介：黄志锋（1998—），男，福建惠安人，硕士研究生，CCF会员，主要研究方向为路径规划、算法优化；刘媛华（1974—），女（通信作者），山东莱阳人，副教授，硕导，博士，主要研究方向为路径规划（liuyuanhua@usst.edu.cn）；任志豪（1997—），男，四川绵阳人，硕士研究生，主要研究方向为路径规划；张文敏（1998—），男，安徽安庆人，硕士研究生，主要研究方向为路径规划；张孝文（1998—），男，河南洛阳人，硕士研究生，主要研究方向为算法优化、博弈．

摘  要：针对动态环境的移动机器人路径规划问题，提出了一种改进哈里斯鹰算法（IHHO）与改进动态窗口算法（IDWA）的融合算法（IHHO-IDWA）。首先，针对哈里斯鹰算法后期搜索性能不足等问题，提出了融合自适应混沌和核心种群动态划分策略、融合黄金正弦策略以及动态云最优解扰动策略来提高算法的性能。其次，针对动态窗口算法存在规划的路径长和易陷入死锁等问题，提出了三个改进策略：增加子函数，保证算法能够规划出更短的路径；提出自适应权重策略，平衡算法局部避障能力和全局搜索性能；设定初始航向角，避免路径冗余。最后，通过测试函数、CEC2014函数的数值实验和静态、动态路径规划实验，验证了IHHO和IDWA性能有明显提升；通过50×50大型动态地图验证了融合算法较对照组算法规划的路径缩短了11.51%，证明了该方法的优越性。

关键词：动态窗口算法；哈里斯鹰算法；自适应；路径规划；测试函数

中图分类号：TP301.6；TP391.9    文獻标志码：A

文章编号：1001-3695（2024）02-020-0450-09

doi：10.19734/j.issn.1001-3695.2023.06.0256

Research on mobile robot dynamic path planning based on improved

Harris hawk algorithm and improved dynamic window algorithm

Huang Zhifeng，Liu Yuanhua，Ren Zhihao，Zhang Wenmin，Zhang Xiaowen

（Business School，University of Shanghai for Science & Technology，Shanghai 200093，China）

Abstract：Aiming at the path planning problem of mobile robot in dynamic environment，this paper proposed a fusion algorithm（IHHO-IDWA） of improved Harris hawk algorithm（IHHO） and improved dynamic window algorithm（IDWA）.First of all，this paper proposed a fusion adaptive chaos and core population dynamic division strategy，a fusion golden sine strategy and a dynamic cloud optimal disturbance resolution strategy to improve the performance of and solve the lack of search performance in the late stage of the Harris eagle algorithm.In addition，in view of the problems that the dynamic window algorithm had a long planned path and easied to fall into deadlock，this paper proposed three improvement strategies to solve them.Firstly，it added sub-functions to ensure that the algorithm could plan a shorter path.Secondly，it proposed an adaptive weight strategy to balance the local obstacle avoidance ability and global search performance of the algorithm.Thirdly，it set the initial heading angle to avoid path redundancy.Finally，through numerical experiments of test functions，CEC2014 functions，and static and dynamic path planning experiments，it is verified that the performance of IHHO and IDWA in this paper has been significantly improved；through the 50×50 large-scale dynamic map，it is verified that the path planned by the fusion algorithm is shorter than that planned by the control group algorithm 11.51%，proving the superiority of the IHHO-IDWA.

Key words：dynamic window algorithm；Harris hawk algorithm；self-adaptation；path planning；test function

0  引言

目前路径规划算法可以分为经典算法和智能优化算法。经典算法如A*算法［1］和RRT算法［2］等；智能优化算法包括粒子群算法［3］、狮群算法［4，5］、鲸鱼优化算法［6］和哈里斯鹰优化算法［7］等。经典算法需要提前载入环境信息，在复杂地图中计算量大，而智能优化算法在已知环境中具有更好的全局性，在未知环境中能够通过测量自身位置与环境的相对信息快速进行路径规划，在复杂环境和未知环境中的路径规划求解上具有优势［8］。哈里斯鹰算法具有参数少、寻优速度快等优点，因此，本文选取哈里斯鹰优化算法进行路径规划研究。

近年来，智能优化算法的路径规划研究成果颇丰。黄志锋等人［9］提出了一种双种群改进狮群算法用于路径规划中，首先在狮群算法基础上引入调节因子和sin混沌提高算法的性能；其次加入方向约束性函数来加快算法向终点靠近，并使用双种群结构提高算法的搜索速度，通过仿真实验验证了改进算法的有效性。刘志强等人［10］针对传统灰狼算法应用在路径规划中收敛效率低的缺陷，首先使用Tent混沌种群初始化，提高解的质量；其次通过改进控制参数H以平衡算法的全局和局部搜索能力；最后在多张地图中验证了改进算法的性能得到了提升。张恒等人［11］提出了一种双层蚁群的路径规划算法，将蚁群分为引导蚁群和普通蚁群，引导蚁群专门应对死锁问题，能够帮助蚁群快速跳出死锁路径。Xu等人［12］提出了一种基于四次Bezier曲线和改进粒子群算法融合的路径规划方法。首先提出了一种加权自适应延迟速度的粒子群算法，提高粒子群的搜索性能；接着，使用四次Bezier曲线对路径进行平滑处理。该方法提高了路径的平滑度和安全性。

总结现有的文献发现，目前路径规划的研究侧重于静态环境的情况较多，有关动态环境的路径规划研究比例相对偏少。然而在实际生产、生活中，通常存在动态障碍物，这时使用静态环境的路径规划算法可能就存在问题。因此，研究动态环境中的路径规划不仅具有理论意义，还具有现实意义。

Molinos等人［13］将动态窗口算法（dynamic window algorithm，DWA）融合动态障碍树法来提高算法的性能，并结合了预测曲率速度法和动态曲率速度法提高路径的安全性。Liu等人［14］利用跳点搜索算法对动态窗口算法进行改进，将跳点搜索改进为新的子函数，并整合全局信息平滑最优路径。Chang等人［15］提出一种基于Q-learning的改进DWA，首先通过增加两个子函数提高全局导航性能；其次，采用Q-learning算法学习机器人路径规划，以适应未知环境。李薪颖等人［16］提出了一种多目标粒子群的动态窗口算法，利用多目标粒子群算法优化DWA参数，使路径能够兼顾安全和运行速度。蒲兴成等人［17］针对动态避障问题提出了结合DWA的改进细菌算法。首先利用细菌算法获得初始路径，再基于初始路径，机器人利用DWA进行动态避障，最后通过实验证明改进算法在性能上有明显提升。魏立新等人［18］提出了基于改进蚁群结合DWA的动态路径规划算法，首先增加了蚁群搜索接力的方式解决了死锁问题，在蚁群算法路径规划完成以后，运用DWA进行局部避障。刘钰铭等人［19］提出了一种结合A*算法和动态窗口的路径规划融合算法，提出自动调整航向角策略，增强算法遇到动态障碍物时的及时避障能力，并针对局部路径规划问题设计了路径偏离评价指标和能耗评价指标。

综上所述，目前关于动态环境的路径规划研究采用的方法多是智能算法融合DWA，虽然上述改进使算法性能有了一定提升，但仍存在改进的空间，例如算法的性能十分依赖参数的设定、在復杂的环境中无法完成路径规划以及路径规划所需时间较长等问题。本文对动态窗口法进行改进，提出三个改进策略来提升算法性能，并融合改进哈里斯鹰算法，利用其较好的全局性优点先进行静态全局路径规划，再进行局部避障，使算法能够应用在动态环境当中。

1  改进哈里斯鹰优化算法

1.1  基础哈里斯鹰优化算法

逃离能量值决定算法执行哪种行为，当逃离能量|E|≥1时执行探索行为，逃离能量变化如下：

E=2E0（1-tT）（1）

其中：E0是（-1，1）的随机初始值；t为当前迭代次数；T为最大迭代次数。

1.1.1  探索行为

当逃离能量|E|≥1时进行随机探索，其更新公式为

X（t+1）=Xk（t）-r1|Xk（t）-2r2X（t）|

（Xk（t）-Xm（t））-r3（lb-r4（ub-lb）） （2）

Xm（t）=1N∑Ni=1Xi（t）（3）

其中：Xk为哈里斯鹰种群中的随机个体；Xr为哈里斯鹰最佳值个体位置；Xm为种群平均位置；N为种群规模；r1～r4 是四个独立服从正态分布［0，1］的随机数；lb和ub为所求问题上下界。

1.1.2  开发行为

当逃离能量|E|<1时进入局部搜索的开发阶段，这时会根据能量值选择四种不同策略进行更新位置。

a）当|E|≥0.5且r≥0.5时，进行软包围，其更新公式为

X（t+1）=ΔX（t）-E|JX（t）-X（t）|（4）

ΔX（t）=Xr-X（t）（5）

其中：J∈［0，2］的随机数，表示算法的步长；ΔX（t）表示最佳位置与当前位置之间的距离。

b）当|E|≥0.5且r<0.5时，算法进行硬包围，其位置更新公式为

X（t+1）=Xr（t）-E|ΔX（t）|（6）

c）当逃离能量值|E|<0.5且r≥0.5时，野兔能量不足，哈里斯鹰采取更为智能的软包围，具体方式为

Y=Xr（t）-E|JXr（t）-X（t）|（7）

Z=Y+S×LF（D）（8）

LF（D）=uσ100×|v|1β，σ=（Γ（1+β）×sin（πβ2）Γ（1+β2）×β×2（β-12））1/β（9）

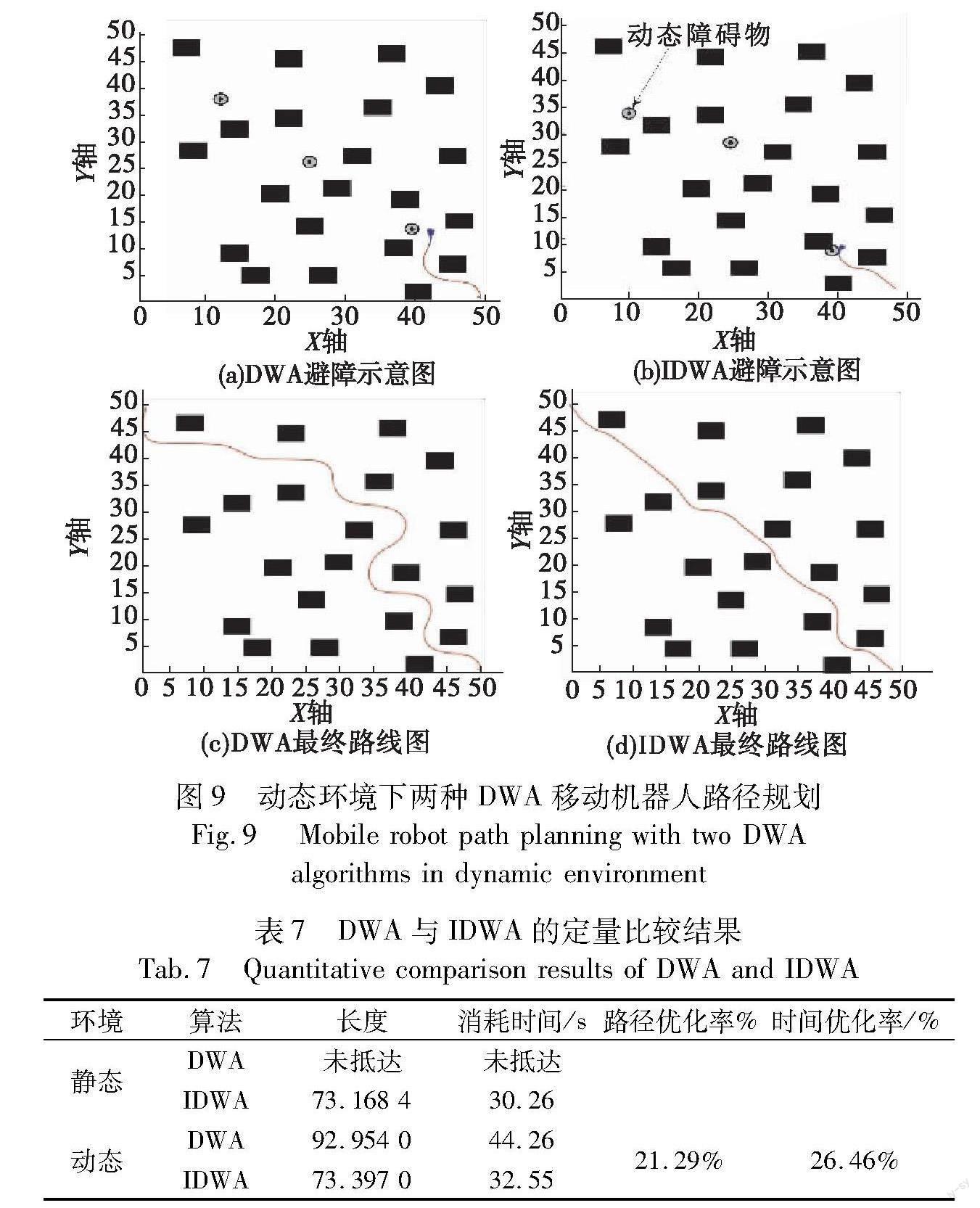
X（t+1）=Yif F（Y）

其中：D是所求问题维度；S是D维上的随机向量；LF（D）是莱维飞行公式；u、v是（0，1）上的随机数；β值为1.5。

d）当|E|<0.5且r<0.5时，采取渐近的软包围，逐步缩短与野兔之间的距离，具体方式为

Y=Xr（t）-E|JXr（t）-Xm（t）|（11）

Z=Y+S×LF（D）（12）

1.2  改进哈里斯鹰优化算法

1.2.1  基于自适应混沌和核心种群动态划分策略

哈里斯鹰优化算法在前期和后期运算中的探索行为和开发行为并不是先后发生，也不是等概率发生。根据式（1），当t=1时也就是第一次迭代，探索概率约为50%；在t=T/2时，E=E0，探索概率为0%，且之后算法也不会再有探索行为。因此，在t

因此，本文提出一种自适应混沌和核心种群动态划分策略。将混沌种群的选取和智能优化算法的收敛优化策略相融合，可以使算法在全局探索和局部搜索之间取得平衡，提高算法的搜索性能和多样性，在哈里斯鹰算法每次行为完成以后且迭代次数超过T/2时进行该操作，这样能弥补哈里斯鹰算法在后期缺乏探索行为的缺点，能够将部分种群释放出去，在远离最优值的位置进行全局随机探索，同时保证在最优值附近充分搜索。

设置一种自适应准线baseline作为划分阈值，之后每次迭代结束后都会将种群重新划分为两种，第一种是以混沌规则在解空间进行全局探索；第二种是遵循智能优化算法收敛规则在领先混沌种群Xr的局部范围内进行逼近搜索，具体流程如下：

a）计算baseline=1T∑Ti=1fit，T为总迭代次数；

b）若当前解X对应的fit

c）若当前解X对应的fit≥baseline，则将X划分为混沌离散种群，称为chaos_swarm；

d）设t為当前迭代次数，tmax为最大迭代次数，计算参数order=size（chaos_swarm）·（t/tmax）2，size（）为种群规模，称order为划分变量；将混沌离散种群从第一个到第order个划分出到核心种群core_swarm中，因为混沌本身具有随机性，所以无须增加随机选取的过程。

如此完成一次划分，baseline会随着迭代次数的变化自适应收敛于fit；此外，混沌种群并不会永远处于混沌当中，在领域周围进行搜索，而是随着迭代次数的增加而减少，会逐渐回归到核心种群，最后只剩极少数还远离核心种群进行随机搜索，且在该过程中游离的混沌种群也会随基线作微小的振荡，反复释放少量的群粒，在混沌操作以后重新进行领域逼近搜索。

Tent混沌种群初始化操作如下：

xk+1=xk/φ0

当φ∈（0，1）且x∈［0，1］时，式（13）处于混沌状态。完成混沌种群初始化构造以后，将所有的群粒以矩阵运算方式输入求解最优适应度fit*及其对应的Xr，该个体称为领先混沌群粒。该划分策略相较于其他文献使用的混沌种群初始化能够保证算法在搜索过程中的多样性。

1.2.2  融合黄金正弦策略

根据式（7）～（10），哈里斯鹰算法采用了一种贪婪策略，如果该策略在软包围冲刺阶段有效，即找到更优解，则更新位置；若该策略失败，没有更优解，则采取式（8）策略，进行莱维飞行扰动；若莱维飞行随机游走失败，没有找到更优解，则退回原解。为了测试莱维飞行游走的效率，采用标准测试函数进行测试，发现加入莱维飞行游走以后，算法收敛精度并没有明显提高；此外，根据文献［20］，软包围策略失败后，莱维飞行的有效率仅为0.03%。因此，本文融合黄金正弦策略替换莱维飞行游走，提高算法性能。

黄金正弦策略［21］于2017年提出，能够快速遍历最优解附近单位圆的所有领域，比莱维随机游走有更强的遍历性。在搜索过程中引入黄金分割系数，确保扫描范围控制在最优解的周围领域，加快算法收敛速度。因此，式（8）和（12）的更新公式变更为

Z=Y+S×R2 sin R1×|x1Xr-x2X（t）|（14）

其中：R1为0～2π的随机数，R2为0～π的随机数，这两个参数决定了算法在下次迭代时的搜索方向和移动距离；x1和x2为黄金分割系数。

x1=-π+（1-δ）2π（15）

x2=-π+δ·2π（16）

δ=0.5（5-1）（17）

1.2.3  融合正态云最优解扰动

为了增强算法后期跳出局部最优解的能力，本文融合了一种自适应正态云最优解扰动策略［22］，越到算法后期，扰动影响越大。正态云模型由云滴论域空间期望Ex、云团不确定性程度熵En和熵不确定性程度超熵He三个参数进行描述。正态云是服从正态分布云滴的一种算法，每一次运行都会生产一个云滴，直到生成期望数量的云滴，其生成过程如下：

X［x1，x2，…，xnd］=Gnc（Ex，En，He，Nd）（18）

其中：Nd表示生成的云滴数量。正态云分布图如图1所示。

Gbest=Xr·［λGnc（Ex，En，He，Nd）］（19）

λ=t2/T2（20）

其中：Gbest表示正态云扰动后的解；t表示当前迭代次数；T表示总迭代次数；λ随着迭代次数增大而增大，到算法后期，最优解受正态云扰动影响也越大。

2  改进动态窗口算法

2.1  基础动态窗口算法

动态窗口法（DWA）是一种用于局部避障的路径规划方法，在DWA中，机器人的速度约束条件如下：

0≤vt≤vmax

vt-amaxΔt≤vt+1≤vt+amaxΔt-ωmax≤ωt≤ωmax

ωt-αmaxΔt≤ωt+1≤ωt+αmaxΔt（21）

其中：vt和ωt分别表示机器人在t时刻的线速度和角速度；vmax和ωmax表示最大速度和最大角速度，vt+1和ωt+1分别为机器人在t+1时刻的线速度和角速度；amax和αmax分别表示最大线加速度和最大角加速度；Δt为时间步长。

可行速度集是通过对运动学模型相适配的速度空间进行采样得到的，并且生成预测轨迹，这些轨迹由评估函数进行评分以找到最佳轨迹和对应的速度集合。评估函数如式（22）所示，包括三个评估子函数及其权重w1、w2和w3，σ表示归一化过程。

J（v，ω）=σ［w1·heading（v，ω）+w2·obdist（v，ω）+

w3·velocity（v，ω）］（22）

heading函数计算机器人在预测轨迹末端的方位角与机器人位置相对于目标方位角之间的角度差，角度差越大，函数值越小；obdist函数计算从预测轨迹的每个点到障碍物的最小距离，该函数用于评估轨迹远离障碍物的程度，函数值越大则距离越大，若轨迹的最小距离小于安全距离，则该轨迹将直接放弃并从采样空间中移除；velocity是评价机器人线速度和角速度的函数，线速度越高，角速度越小，得分越高。

若要求算法的全局搜索能力较强时，则权重w1设置较大一些；若要求机器人有较好的避障能力，则权重w2设置较大一些；若要求机器人行走路径更平滑，则权重w3设置大一些。

基础动态窗口算法在路径规划方面的应用仍存在一些局限性：a）动态窗口进行动态避障后规划的路径与智能优化算法规划的路径有一定差距，这也会增加路径长度；b）动态窗口法与智能优化算法不同，没有设定一个初始的搜索方向，这也会增加路径长度；c）子函数权重是固定值，在靠近障碍物时w2应该设定较大进行避障，但这会削弱算法全局搜索性能，若w2设定过小就会撞上障碍物，且在复杂环境中基础动态窗口出现无法规划出路径的情况。因此，本文提出三個策略以解决动态窗口算法存在的缺陷。

2.2  改进动态窗口算法

2.2.1  策略1：增加子函数pathdist（v，ω）

融合算法的原理是，在全局信息已知的条件下，先通过智能优化算法计算出静态环境下的最短路径，记作minpath。机器人开始沿着该路径行走，同时对周围环境进行扫描，当遇到动态障碍物时进行避障，改变当前路径。此时，基础动态窗口规划的路径有可能会远离最短路径，为了保证规划出的路径最短，本文增加子函数pathdist（v，ω），其权重系数为w4。子函数的作用就是使算法选择最靠近智能优化算法规划出的路径，改进后的动态窗口算法评估函数为

J（v，ω）=σ［w1·heading（v，ω）+w2·obdist（v，ω）+

w3·velocity（v，ω）+w4·pathdist（v，ω）］（23）

dp1=（x1-xp1）2+（y1-yp1）2（24）

ψ=dp1+dp2+dp3+dp4+dp55（25）

pathdist=1ψ（26）

式（24）表示预测轨迹的起点到minpath的最短距离；dp1…dp5分别表示预测轨迹上均等分的五个点到路径minpath的最短距离；（x1，y1）表示预测轨迹上第一个点的坐标；（xp1，yp1）为预测轨迹上第1个点到路径minpath最短距离上的点；ψ表示衍射线5个点到minpath最短距离的加权平均距离，ψ越小，表示该预测轨迹与minpath最接近，pathdist的值就越大，评分就越高。算法会优先选择评分高的路径，这样能使动态窗口算法规划出的路径最接近智能优化算法规划出的minpath。

2.2.2  策略2：自适应权重策略

在远离障碍物时，算法需要较强的局部搜索能力，靠近障碍物时需要较强的局部避障能力，但基础动态窗口算法中各权重系数是固定的；此外在实验中发现，如果动态障碍物的速度过快，就会使动态窗口算法避障不及时，碰上障碍物。因此本文提出自适应权重，当机器人靠近至障碍物一定距离后，自适应控制权重w2增加，使算法具有更强的避障能力。具体思路如下：

首先计算机器人在当前时刻的空间位置和障碍物之间的最短距离：

dro=（xr-xo）2+（yr-yo）2（27）

dall=（xs-xe）2+（ys-ye）2（28）

其中：dro表示机器人与障碍物之间的距离；（xr，yr）表示机器人当前坐标位置；（xo，yo）表示动态障碍物的坐标位置；dall表示起点到终点的距离；（xs，ys）表示起点坐标位置；（xe，ye）表示终点坐标位置。

w2=（vt+ωt）×dalldro（29）

其中：vt和ωt分别表示机器人在t时刻的线速度和角速度。由此可知，w2权重大小与速度和角速度成正比，与距离dro成反比，当机器人速度越快、越靠近障碍物时，w2权重越大，避障能力越强。

2.2.3  策略3：设定动态航向角

动态窗口算法的初始方向和初始航向角的设定是随机的，当与目标栅格角度偏差过大时，会出现初期绕行甚至陷入死锁无法规划出完整路径的现象。因此，本文提出以起点与第一个子目标点的连线和水平方向的夹角来动态规定初始方向，防止机器人绕行。

为了避免子目标点选择不正确导致角度偏差带来的影响，对起点周围的节点进行筛选处理，根据周围节点到目标点距离设置距离估值评分函数。具体操作如下：设（xs，ys）为当前点，（xjn，yjn）为下一可行节点（没有障碍物即可算作可行节点），（xgoal，ygoal）为目标节点。假设当前点周围不存在障碍物，均为可行区域，则n=1，2，3，…，8。分别计算可行节点距离估值评分函数的值：

h（dn）=d-min d（max d-min d）+ep（30）

其中：d=dsjn+djng，dsjn表示当前节点到下一可行节点n的距离，djng表示下一可行节点n到目标节点的距离； min d表示可行节点到目标节点和当前节点距离之和最短的距离；max d表示可行节点到目标节点和当前节点距离之和最长的距离；ep表示很小的数，避免分母为0。当下一可行节点离目标点越近，该函数值就越大，下一节点离终点越近；该函数值越小，下一节点离终点越远。最后对可行节点进行排序，选择函数值最大的节点做为第一个子目标点。

（xs，ys）为起点坐标，假设（x1，y1）为第一个子目标点，则初始航向角规定为

φ=arcsin c（31）

c=y1-ysdr1（32）

dr1=（x1-xs）2+（y1-ys）2（33）

其中：c是初始航向角的正弦值；dr1表示机器人到第一个子目标点的距离。

图2（a）（b）是航向角对算法的影响示意图。图2（a）是未改进初始航向角的动态窗口算法，其一开始就绕行，而改进后的算法直接向下一个目标点行走，避免了路径冗余。

2.3  融合算法流程

改进动态窗口算法结合改进哈里斯鹰优化算法的融合算法，以下简称IHHO-IDWA，其具体流程如图3所示。

3  实验结果及分析

实验环境：操作系统Windows 11（64bit），处理器AMD Ryzen 7 5800H with Radeon Graphics.3.20 GHz，运行内存16 GB，仿真平台MATLAB 2021a。

为了验证改进哈里斯鹰算法和改进动态窗口算法的性能，设置了以下四组实验：

a）数值实验。设置国际通用测试函数和CEC2014函数验证IHHO算法的性能。对照组算法为传统算法GA、PSO，新型智能优化算法GWO、HHO，改进智能优化算法DCSOA-S［23］（融合螺旋策略的离散混沌群粒振荡搜索算法）和GHHO［24］（融合能量周期性递减与牛顿局部增强的改进HHO算法）。

b）路径规划实验。设置两张不同大小的地图，验证IHHO算法在路径规划中具有较好的性能。

c）动态窗口路径规划实验。验证IDWA比基础DWA具有更好的性能。

d）融合算法实验。验证IHHO-IDWA的性能。对照组算法为PSO-DWA、HHO-DWA和DLSO-DWA。

参数设置：其中GA交叉概率Pc=0.8，变异概率Pm=0.1；PSO学习因子c1=2，c2=2，惯性权重ω=0.8；GWO系数A=2；DLSO哈里斯磨β=0.3。

为保证实验公平性，每次实验重复10次，每次算法运行10轮，统计其平均值和标准差。

3.1  数值实验

为验证本文所提改进哈里斯鹰算法（IHHO）的性能，选择了9个国际标准测试函数进行验证，如表1所示。其中f1～f3是多维单峰函数，用于检测算法局部搜索性能；f4～f6是多峰函数，用于检验算法全局寻优能力；f7～f9为固维函数，检验算法平衡全局和局部搜索的能力。本次实验统一设置维度D=30、种群规模N=30、T=500，各算法一致。

从表2的实验结果可以看出，IHHO算法在f1～f3多峰函数的寻优中较基础的HHO和GHHO有明显的提升，且IHHO都找到了最优值，证明黄金正弦策略能够帮助IHHO有更好的局部搜索能力；对于f4～f6多峰函数，IHHO较传统算法GA、PSO和DCSOA-S，搜索的均值和标准差更小，证明IHHO有更好的稳定性和全局搜索性能；对于固维函数f7～f9的搜索表现，IHHO算法和DCSOA-S算法性能相差不大，但相较于HHO和GHHO的平均值和标准差更小，搜索精度更高，且都搜索到了最优值，证明了自适应混沌和核心种群划分策略，提高了算法平衡全局和局部搜索的能力。总体而言，改进IHHO算法性能最优，算法在稳定性、局部搜索能力以及全局搜索能力均有提升，说明融合三個改进策略能够明显提升算法性能。图4为部分测试函数收敛曲线。

接下来选取了6个CEC2014测试函数，该函数更为复杂，分别有单峰函数（UN）、多峰函数（MN）、混合型函数（HF），如表3所示。表4为实验结果，图5为部分CEC2014函数的收敛曲线。

从表4可知，IHHO在更复杂的单峰、多峰和混合型函数寻优中，IHHO的寻优平均值和标准差比HHO算法提高了1～2个量级，提升明显，证明了IHHO算法具有更好的稳定性和寻优能力。IHHO算法在对照组算法中性能最优。

3.2  基于改进哈里斯鹰的移动机器人路径规划

本节通过路径规划实验来验证本文算法的性能。实验中种群规模N=30，迭代次数T=50。

为了对比改进前后的效果，定义优化率为

η=μm-μ0μ0=Δμμ0（34）

其中：μm表示改进后算法规划路径的长度和算法运行时间；μ0表示改进前算法的路径长度和算法运行时间。该等式能够直接反映算法的优化程度。

3.2.1  40×40静态地图实验

首先设置一张40×40的中型地图，障碍物占比约为23%，验证改进算法的性能，结果如表5和图6所示。

从表5和图6实验结果可知，IHHO算法在40×40地图表现中性能最优，搜索到的最短路径为62.769 6，较其他算法缩短了8.20%，运行时间也最短，证明了IHHO算法在路径规划中具有较好的搜索性能。图6中，（a）为算法迭代曲线，（b）～（g）为各算法规划出的路径。

3.2.2  50×50静态地图实验

设置一张50×50，障碍物占比约为25%的大型地图来验证改进算法的性能。图7为各算法的规划结果。

从表6的实验结果可知，在50×50地图实验中，IHHO规划出的路径最短，为78.669 0 m，相比其他算法缩短了12.66%，平均路径缩短了13.84%，算法运行时间也最短，IHHO算法在路径规划中表现优异，性能提升明显。此外，从图7可以看出，IHHO规划出的路线最平滑，没有路径冗余。

3.3  基于改进动态窗口的移动机器人路径规划

为验证本文改进的动态窗口算法在移动机器人路径规划中的性能，将改进后的动态窗口算法（IDWA）与基础动态窗口法（DWA）进行比较，分别在静态和动态环境进行测试。

3.3.1  改进动态窗口法在静态地图中的性能分析

首先在50×50的静态地图中进行实验，设置起点坐标为（50，0），终点坐标为（0，50），实验结果如图8所示。

从图8可以看出，在静态地图中，DWA没有规划出路径，陷入了死锁，在坐标（10，30）的位置时开始绕圈，无法到达终点；而IDWA能够很好地完成路径规划，说明自适应权重能够更好地平衡IDWA的搜索性能和避障性能。

3.3.2  改进动态窗口法在动态地图中的性能分析

在50×50的动态地图当中进行实验，设置三个动态障碍物不间断移动，黑色圈代表动态障碍物。起点为（49，1），终点为（1，49），实验结果如图9所示。

图9（a）（b）分别是DWA和IDWA正在进行避障的过程，（c）（d）分别是DWA和IDWA规划出的最终路线图。可以看到，DWA规划出的路径一开始是向上行走，而IDWA规划出的路径一开始就是向终点行走，能缩短路程，且IDWA规划的路径能更少地绕弯，整体上规划的路径更优。

在静态地图中，DWA陷入死锁，没有规划出路径，而IDWA完成了路径规划。如表7所示，在动态地图中，IDWA规划出的路径相比DWA缩短了21.29%，时间上减少了26.46%。因此，IDWA的性能得到了明显的提升。

3.4  IDWA和IHHO融合算法动态地图实验

本节将IDWA和IHHO结合，改进哈里斯鹰算法融合改进动态窗口算法（IHHO-IDWA）来进一步验证算法性能，同时设置对照组算法分别为灰狼算法与动态窗口（GWO-DWA）、哈里斯鹰算法与动态窗口（HHO-DWA），双种群混沌柯西变异的改进狮群算法［9］与动态窗口（DLSO-DWA）三种算法。

设置50×50大小的地图，障碍物占比约为25%，设置四个动态障碍物。从表8的实验结果来看，IHHO-IDWA性能最优。

图10是IHHO-IDWA路径规划的过程，选取了部分截图，虚线是IHHO先进行规划的最短路径，红色路线是启动IDWA进行实时避障的路线（参见电子版）。图10中，（a）是机器人碰到的第一个动态障碍物，进行避障；（b）显示机器人绕开动态障碍物之后，沿着IHHO规划出的路径行走；（c）显示机器人受到障碍物的影响，机器人行走路线与IHHO有所偏离，但之后又马上回归到IHHO规划的路线；（d）显示算法规避动态障碍物。

3.5  参数敏感性分析

实验中设置的种群规模和总迭代次数可能会影响实验结果，在实验环境和算法其他参数不变的情况下，在40×40和50×50地图进行参数敏感性实验。为避免偶然性，重复十次实验，取结果的平均值。图11为种群敏感性分析。

从图11的分析结果得知，在40×40地图中，种群规模在N=30时，算法搜索到最优值，继续增加种群规模，并不影响算法搜索的结果。在50×50地图中，种群规模在30～40搜索到最优值，但是随着种群规模的增加，算法运行时间也增加，综合考虑种群规模和运行时间，选择N=30。

图12是迭代次数对寻优结果的影响分析。可以看到，在40×40地图中，迭代次数为30时基本收敛，不会继续搜索到最优值。在50×50地图中，算法在迭代40次左右时收敛到最优值。迭代次数越多，运算时间越长，因此综合考虑，T=50。

4  結束语

针对动态环境下的移动机器人全局路径规划问题，本文提出了一种改进哈里斯鹰算法和改进动态窗口算法的融合算法。首先，针对哈里斯鹰算法后期搜索性能不足等问题，提出一种自适应混沌和核心种群划分策略，提高算法后期全局搜索性能；其次用黄金正弦替换原有的莱维飞行，提高算法的搜索效率；最后，融合正态云最优解扰动提高算法后期跳出局部最优解的能力。针对基础动态窗口算法存在规划的路径长和易陷入死锁等问题，提出了三个改进策略：增加子函数pathdist（v，ω）保证算法能够规划出更短的路径；提出自适应权重策略，平衡算法局部避障能力和全局搜索性能；设定初始航向角避免路径冗余。最后，本文通过三组实验分别验证了改进哈里斯鹰算法、改进动态窗口算法与融合算法的性能。结果显示，本文提出的融合算法路径最短，路径平均缩短了11.51%，性能提升显著。

参考文献：

［1］Hart P E，Nilsson N J，Raphael B.A formal basis for the heuristic determination of minimum cost paths［J］.IEEE Trans on Systems Science and Cybernetics，1968，4（2）：100-107.

［2］Kuffner J J，LaValle S M.RRT-connect：an efficient approach to single-query path planning［C］//Proc of IEEE International Confe-rence on Robotics and Automation.Piscataway，NJ：IEEE Press，2000：995-1001.

［3］孙睿彤，袁庆霓，衣君辉，等.改进粒子群算法和动态窗口法的动态路径规划［J］.小型微型计算机系统，2023，44（8）：1707-1712.（Sun Ruitong，Yuan Qingni，Yi Junhui，et al.Dynamic path planning by combing the improved particle swarm algorithm and dynamic window approach［J］.Journal of Chinese Computer Systems，2023，44（8）：1707-1712.）

［4］黄志锋，刘媛华，张聪.多策略融合的改进狮群算法及其工程优化［J/OL］.小型微型计算机系统（2023-02-09）.https：doi.org/10.20009/j.cnki.21-1106/TP.2021-0600.（Huang Zhifeng，Liu Yuanhua，Zhang Cong.Multi-strategy fusion improved lion swarm algorithm and its engineering optimization［J/OL］.Journal of Chinese Computer Systems（2023-02-09）.https：doi.org/10.20009/j.cnki.21-1106/TP.2021-0600.）

［5］黄志锋，刘媛华.基于改进狮群算法的城市无人机低空路径规划［J］.信息与控制，2023，52（6）：747-757，772.（Huang Zhifeng，Liu Yuanhua.Urban UAV low altitude path planning based on improved lion swarm algorithm［J］.Information and Control，2023，52（6）：747-757，772.）

［6］Mirjalili S，Lewis A.The whale optimization algorithm［J］.Advances in Engineering Software，2016，95（5）：51-67.

［7］Heidari A A，Mirjalili S，Faris H，et al.Harris hawks optimization：algorithm and applications［J］.Future Generation Computer Systems，2019，97（8）：849-872.

［8］陈麒杰，晋玉强，韩露.无人机路径规划算法研究综述［J］.飞航导弹，2020（5）：54-58.（Chen Qijie，Jin Yuqiang，Han Lu.Review of UAV path planning algorithms［J］.Aerospace Technology，2020（5）：54-58.）

［9］黄志锋，刘媛华.基于四阶贝塞尔曲线和改进狮群优化算法求解路径规划问题［J］.信息与控制，2023，52（2）：176-189.（Huang Zhifeng，Liu Yuanhua.Solving path planning problem based on fourth-order Bezier curve and improved lion swarm optimization algorithm［J］.Information and Control，2023，52（2）：176-189.）

［10］劉志强，何丽，袁亮，等.采用改进灰狼算法的移动机器人路径规划［J］.西安交通大学学报，2022，56（10）：49-60.（Liu Zhiqiang，He Li，Yuan Liang，et al.Path planning of mobile robot based on TGWO algorithm［J］.Journal of Xian Jiaotong University，2022，56（10）：49-60.）

［11］张恒，何丽，袁亮，等.基于改进双层蚁群算法的移动机器人路径规划［J］.控制与决策，2022，37（2）：303-313.（Zhang Heng，He Li，Yuan Liang，et al.Mobile robot path planning using improved double-layer ant colony algorithm［J］.Control and Decision，2022，37（2）：303-313.）

［12］Xu Lin，Cao Maoyong，Song Baoye.A new approach to smooth path planning of mobile robot based on quartic Bezier transition curve and improved PSO algorithm［J］.Neurocomputing，2022，473（2）：98-106.

［13］Molinos E J，Llamazares A，Ocaa M.Dynamic window based approaches for avoiding obstacles in moving［J］.Robotics and Autonomous Systems，2019，118（8）：112-130.

［14］Liu Lisang，Yao Jinxin，He Dongwei，et al.Global dynamic path planning fusion algorithm c ombining jump-A* algorithm and dynamic window approach［J］.IEEE Access，2021，9：19632-19638.

［15］Chang Lu，Shan Liang，Jiang Chao，et al.Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment［J］.Autonomous Robots，2021，45（1）：51-76.

［16］李薪穎，单梁，常路，等.复杂环境下基于多目标粒子群的DWA路径规划算法［J］.国防科技大学学报，2022，44（4）：52-59.（Li Xinying，Shan Liang，Chang Lu，et al.DWA path planning algorithm based on multi-objective particle swarm optimization in complex environment［J］.Journal of National University of Defense Technology，2022，44（4）：52-59.）

［17］蒲兴成，谭令.基于自适应动态窗口改进细菌算法与移动机器人路径规划［J］.智能系统学报，2023，18（2）：314-324.（Pu Xingcheng，Tan Ling.A mobile robot path planning method based on adaptive DWA and an improved bacteria algorithm［J］.CAAI Trans on Intelligent Systems，2023，18（2）：314-324.）

［18］魏立新，张钰锟，孙浩，等.基于改进蚁群和DWA算法的机器人动态路径规划［J］.控制与决策，2022，37（9）：2211-2216.（Wei Lixin，Zhang Yukun，Sun Hao，et al.Robot dynamic path planning based on improved ant colony and DWA algorithm［J］.Control and Decision，2022，37（9）：2211-2216.）

［19］刘钰铭，黄海松，范青松，等.基于改进A* DWA算法的移动机器人路径规划［J/OL］.计算机集成制造系统.（2022-11-28）.https：//kns.cnki.net/kcms/detail/11.5946.TP.20221125.1957.004.html.（Liu Yuming，Huang Haisong，Fan Qingsong，et al.Based on improved A*_DWA algorithm for mobile robot path planning［J/OL］.Computer Integrated Manufacturing System.（2022-11-28）.https：//kns.cnki.net/kcms/detail/11.5946.TP.20221125.1957.004.html.）

［20］刘小龙，梁彤缨.基于方形邻域和随机数组的哈里斯鹰优化算法［J］.控制与决策，2022，37（10）：2467-2476.（Liu Xiaolong，Liang Tongying.Harris hawk optimization algorithm based on square neighborhood and random array［J］.Control and Decision，2022，37（10）：2467-2476.）

［21］Tanyildizi E，Demir G.Golden sine algorithm：a novel math-inspired algorithm［J］.Advances in Electrical and Computer Engineering，2017，17（2）：71-78.

［22］李德毅，刘常昱.论正态云模型的普适性［J］.中国工程科学，2004，6（8）：28-34.（Li Deyi，Liu Changyu.Study on the universality of the normal cloud model［J］.Strategic Study of CAE，2004，6（8）：28-34.）

［23］林之博，刘媛华.融合螺旋策略的离散混沌群粒振荡搜索算法［J］.计算机应用研究，2021，38（10）：3060-3066，3071.（Lin Zhibo，Liu Yuanhua.Dispersed chaotic swarm oscillation algorithm merged with spiral strategy［J］.Application Research of Computers，2021，38（10）：3060-3066，3071.）

［24］赵世杰，高雷阜，于冬梅，等.融合能量周期性递减与牛顿局部增强的改进HHO算法［J］.控制与决策，2021，36（3）：629-636.（Zhao Shijie，Gao Leifu，Yu Dongmei，et al.An improved HHO algorithm combining periodic energy decrease and Newton local enhancement［J］.Control and Decision，2021，36（3）：629-636.）