约束二进制二次规划测试函数的一个构造方法

雍龙泉

(陕西理工学院 数学与计算机科学学院， 陕西 汉中 723000)



约束二进制二次规划测试函数的一个构造方法

雍龙泉

(陕西理工学院 数学与计算机科学学院， 陕西 汉中 723000)

[摘要]基于盖尔圆定理, 给出了约束二进制二次规划测试函数的一个构造方法: 对原问题, 通过线性变换, 得到一个新的不定二次规划, 且该不定二次规划恰好以给定初始点为最优解; 进而构造出了一系列具有共同最优解的约束二进制二次规划。

[关键词]二进制二次规划;测试函数;半正定矩阵;盖尔圆定理

非线性整数规划在经济、计算机科学、工程技术中有非常重要的应用。 多年的研究表明, 非线性整数规划是数学规划和运筹学中最困难的研究领域之一。 即使是形式上看起来很简单的线性约束二次整数规划在全空间上求解也是不可判定的, 即不存在求解该问题的算法。 因此, 在求解非线性整数规划问题时, 往往要假定是在有界闭箱上进行求解。 0-1二次规划是一类特殊的非线性整数规划, 国外学者Barhona和Hansen对0-1二次规划做了大量的研究, 并且给出了一些具体的实例[1-2]；国内学者对0-1二次规划也做了大量的研究, 得到了一些比较好的结果[3-5]。 总体上说, 求解非线性整数规划问题的方法到目前为止还不多, 现有的算法可分为3类：(1)化为等价问题，主要包含化为连续优化问题的方法和线性化为整数规划问题的方法； (2)分支定界法，对目标函数和约束函数是可定界的非线性整数规划问题, 这种方法是适用的；(3)近似方法，是为了尽快找到问题好的但未必是最优解而设计的方法, 主要包括随机方法和局部搜索方法[7-11]。

衡量一个算法的优与劣, 就需要利用算法做相应的数值实验进行测试。 而做数值实验时, 就要求所给的测试问题的最优解已知；只有知道了测试问题的最优解之后, 那么用设计的算法来进行测试, 再用计算后的结果和已知最优解做比较, 这样才能知道算法的优劣。因此, 如何构造测试问题(验证算法的好与差), 这就成了计算数学的难点。 本文初步给出了约束二进制二次规划测试函数的一个构造方法: 用给定的可行点z0和矩阵M构造出了一系列的约束二进制二次规划, 使得这些二进制二次规划都具有共同的最优解。

1预备知识

定理1设A是n×n的实对称矩阵, 则A的特征值皆为实数。

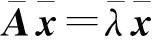
用x右乘上式, 得

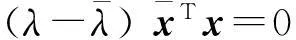
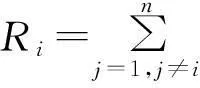
定理2(盖尔圆定理) 矩阵A=(aij)∈Cn×n的一切特征值都在它的n个盖尔圆的并集之内。

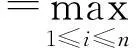
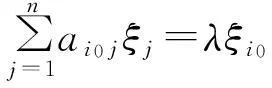
也就是λ∈Gi0,当然λ也在A的n个盖尔圆Gi(i=1,2,…,n)的并集之内。

定理3由矩阵A的所有盖尔圆组成的连通部分中任取一个, 如果它是由k个盖尔圆构成的, 则在这个连通部分中有且仅有A的k个特征值(盖尔圆相重时重复计数, 特征值相同时也重复计数)。

定理3的证明见文献[12]。

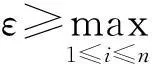
下面通过例子来说明上述定理的应用。

本文利用盖尔圆定理得到了一系列ε使得M+εI半正定,此结果比文献[13]中的结论更完善, 更具有普遍性。

2测试函数的构造方法

考虑如下形式的二进制二次规划

其中c∈Rn,Q是n×n的实对称矩阵,S是一个非空凸集。

作线性变换z=e-2x,其中eT=(1,1,…,1)。由于z=e-2x,也即x=(e-z)/2, 代入(QP1) 的目标函数中得到

(-c/2-Qe/4)Tz+zT(Q/4)z/2+cTe/2+eTQe/8,

若记a=-c/2-Qe/4,M=Q/4, 则(QP1)可以转化为

注：通过线性变换z=e-2x,把x∈S变换为z∈D(由于S是非空凸集,故D也是非空凸集);(QP2)与(QP1)的最优解相同,其目标值仅相差一个常数k=cTe/2+eTQe/8。

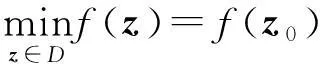
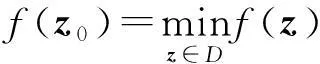
证明考虑辅助函数

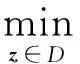
因此, 对任意的z∈D,z∈{-1,1}n,都有φ(z)≥φ(z0),即

(1)

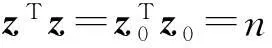
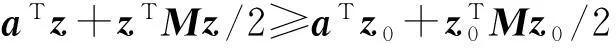
(2)

由(2)式知道,对任意的z∈D,z∈{-1,1}n,都有f(z)≥f(z0);这表明所构造的f(z)恰好在z0点达到最优。

下面给出约束二进制二次规划测试函数的构造方法。

例3z∈D,z∈{-1,1}2,其中集合D={(z1,z2)|z1+z2≤1,2z1-3z2≤5,-z1≤2},给一个可行点z0=(1,-1)T和一个n×n的实对称矩阵M1(显然这里M1不定), 利用前面例1的结果,当ε≥3时M1+εI为半正定矩阵。

若取ε=3, 则a=-(M1+εI)z0=(0,2)T, 对应的目标函数

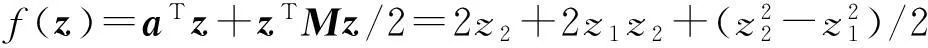
此时, 相应的(不定)二次规划为

由定理4可知, (QP3)的最优解为z*=z0=(1,-1)T。

再利用线性变换z=e-2x,得到相应的约束二进制二次规划

且该约束二进制二次规划的最优解为x*=(0,1)T。

进而,当ε≥3,比如取ε=4,5,6,…,可以得到一系列的二进制二次规划, 使得这些二进制二次规划都具有共同的最优解x*=(0,1)T。

例4z∈D,z∈{-1,1}4,其中集合

给一个可行点z0=(-1,-1,-1,1)T和一个n×n的实对称矩阵M2(显然这里M2不定), 利用前面例2的结果, 当ε≥5时M2+εI为半正定矩阵。

若取ε=5,则a=-(M2+εI)z0=(6,8,4,-2)T,对应的目标函数

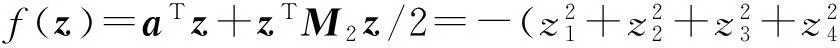
此时,相应的(不定)二次规划为

由定理4可知,(QP5)的最优解为z*=z0=(-1,-1,-1,1)T。

再利用线性变换z=e-2x, 得到相应的约束二进制二次规划

且该约束二进制二次规划的最优解为x*=(1,1,1,0)T。

进而, 当ε≥5,比如取ε=6,7,8,…,可以得到一系列的二进制二次规划,使得这些二进制二次规划都具有共同的最优解x*=(1,1,1,0)T。

例如取ε=1×104,得到如下约束二进制二次规划(QP7)为

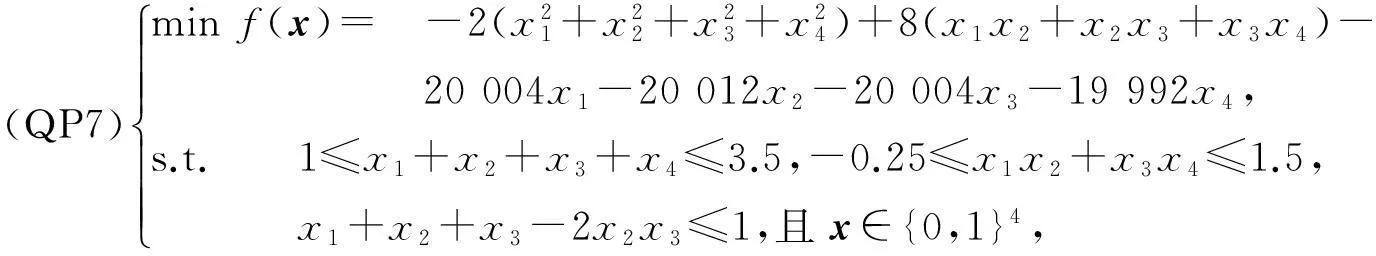
且该约束二进制二次规划的最优解也是x*=(1,1,1,0)T。

3测试函数的验证

为了验证所构造测试函数的准确性，用LINGO软件分别就(QP4)、(QP6)和(QP7)进行了求解，所得的结果见图1—图3。

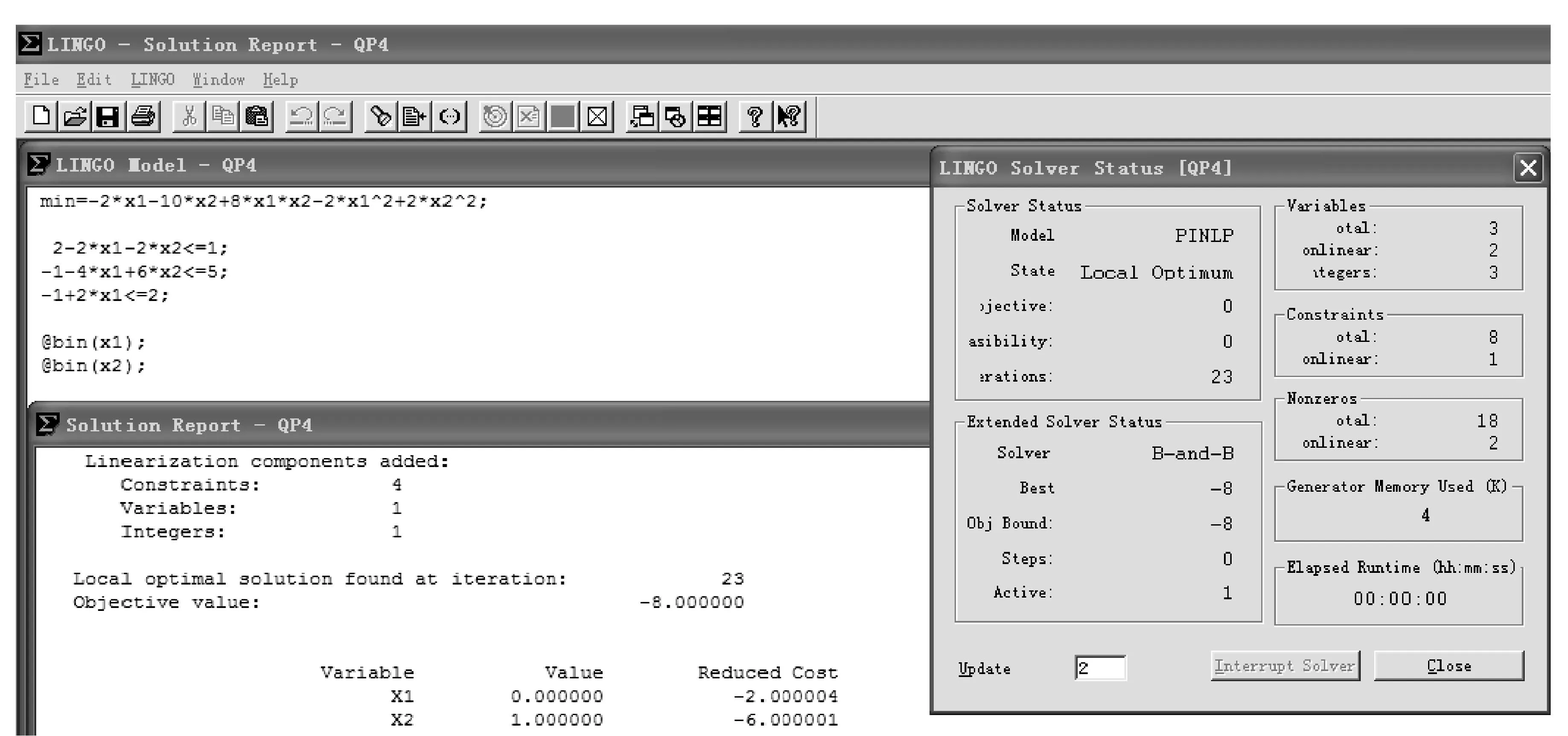
图1　(QP4)的LINGO代码及求解结果

LINGO软件求解结果进一步表明, 本文构造的测试函数是正确的。

4结束语

本文给出了约束二进制二次规划测试函数的一个构造方法。 因此, 在对约束二进制二次规划的算法做数值实验的时候, 就不必再拿经典的例子[14]做测试, 而改用本文构造的算例进行测试, 这在很大程度上丰富了算法的数值实验结果。

图2　(QP6)的LINGO代码及求解结果

图3　(QP7)的LINGO代码及求解结果

[1]BARAHONA F. A solvable case of quadratic 0-1 programming[J]. Discrete Applied Mathematics, 1986, 13(1): 23-26.

[2]HANSEN P. Methods of Nonlinear Zero-one Programming[J]. Annals Discrete Math，1979(5):53-70.

[3]陈伟.0-1二次规划的全局最优性条件及算法[D]. 上海: 上海大学, 2005.

[4]邓俊威.线性约束下0-1二次规划问题的研究[D].北京: 清华大学, 2010.

[5]黄红选.全局优化引论[M].北京: 清华大学出版社, 2005: 54-110.

[6]ADAMS W P,Forrester R J,Glover F W.Comparisons and enhancement strategies for linearizing mixed 0-1 quadratic programs [J].Discrete Optimization,2004,1(2):99-120.

[7]PAN S H,TAN T,JIANG Y X.A global continuation algorithm for solving binary quadratic programming problems[J].Computational Optimization and Applications,2007,41(3):349-362.

[8]HE S,LUO Z Q,NIE J,et al.Semidefinite relaxation bounds for indefinite homogeneous quadratic optimization [J].SIAM J Optim,2008,19(2):503-523.

[9]ENDRE B,HAMMER P L,SUN R,et al.A max flow approach to improved lower bounds for quadratic unconstrained binary optimization (QUBO) [J].Discrete Optimization,2008,5(2):501-529.

[10]PARDALOS P M,PROKOPYEV O A,SHHLO O V,et al.Global equilibrium search applied to the unconstrained binary quadratic optimization problem [J].Optimization Methods and Software,2008,23(1):129-140.

[11]MU X W,ZHANG Y L,LIU S Y.A new branch and bound method with pretreatment for the binary quadratic programming [J].Applied mathematics and computation,2008,192(1):252-260.

[12]程云鹏.矩阵论[M].2版.西安: 西北工业大学出版社,2001:234-249.

[13]PARDALOS P M.Construction of Test Problems in Quadratic Bivalent Programming [J].ACM Transactions on Mathematical Software,1991,17(1):74-87.

[14]李兴斯, 谭涛.求解二进制二次规划问题的一种连续化方法[J].工程数学学报,2006,23(3):499-504.

[责任编辑：张存凤]

Method of constructing test problems for constrained binary

quadratic programming

YONG Long-quan

(School of Mathematics and Computer Science, Shaanxi University of Technology,

Hanzhong 723000, China)

Abstract:Based on Gerschgorin’s disk theorem, a method of constructing test function with known global solution for a class of constrained binary quadratic programming is presented. By using the linear transformation, a new indefinite quadratic programming is obtained, whose minimum occurs at the initial point over the given domains. Furthermore, a series of binary quadratic programming that has a common optimal solution is constructed.

Key words:binary quadratic programming;test function;positive semidefinite matrix;Gerschgorin’s disk theorem

作者简介：雍龙泉(1980—), 男, 陕西省洋县人, 陕西理工学院副教授, 主要研究方向为最优化理论与算法。

基金项目：陕西理工学院科研计划项目(SLGKYQD2-14)

收稿日期：2014-12-18

[中图分类号]O224

[文献标识码]A

[文章编号]1673-2944(2015)06-0051-06