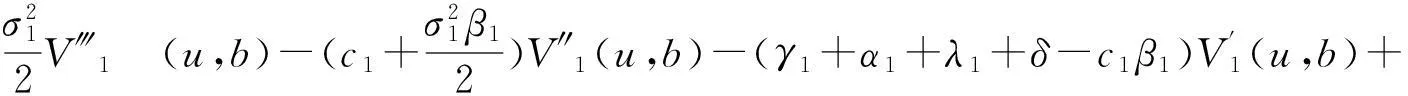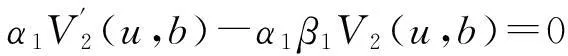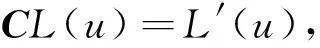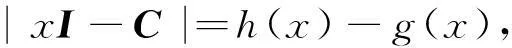一类对偶风险模型随机观察下的边界分红

张　娜，　王秀莲

(天津师范大学 数学科学学院,天津 300387)



一类对偶风险模型随机观察下的边界分红

张娜，王秀莲

(天津师范大学 数学科学学院,天津 300387)

[摘要]分红问题是金融保险研究的重要内容之一。针对带扰动的马氏对偶风险模型，考虑了其随机观察下的边界分红问题。根据收益到达发生、分红发生和环境状态改变3个因素，利用重期望公式得到了破产前累积分红折现期望在不同初始盈余下所满足的积分-微分方程；进一步求得了在马氏过程仅有两个状态情形下收益为指数分布时的累积分红折现期望。

[关键词]对偶风险模型；马氏调制；随机观察；累积分红折现期望

1引言与模型介绍

经典对偶风险模型为U(t)=u-ct+S(t)+σW(t),t≥0。针对此类模型有较多的研究,如:Cremer H[1]研究了经典对偶风险模型;Zhu Jin-xia等[2]研究了对偶风险模型的破产概率;Ma Xue-min等[3]研究了两状态下对偶风险模型的常数边界策略;Andrew C.Y. Ng[4]研究了具有分红临界值的对偶风险模型;Avanzi B等[5-6]研究了对偶模型最优分红问题。但是这些成果都没有考虑外部环境过程对公司的影响，实际上，公司的收益到达过程、收益额大小、扩散系数以及分红等都会受外部环境的影响，因此许多学者考虑了受马氏调制的风险模型，如:Lu Yi[7]研究了马氏风险模型破产程度;Zhu Jin-xia等[8]研究了马氏对偶风险模型破产函数的可微性;Liu Dong-hai等[9]研究了常数值分红策略下带扰动的马氏调制对偶风险模型;Benjamin Avanzi等[10]研究了带扰动对偶模型的最优分红策略。

分红问题作为风险模型的重要问题，受到了许多学者的关注，然而多数学者考虑的分红关于时间都是连续进行的。实际上，公司可能会在定期的但不完全确定的时间下进行账本审核，如每年进行一次或每时期进行一次，这样考虑随机观察下的分红更为切合实际。随机观察下的边界分红问题是指公司仅在盈余大于常数值分红策略b且被观察者观察到的情形下进行分红，并将超出b的部分全部分红。如果公司的资金超过b但未被观察到，那也就不分红。如果破产发生，则保险公司不再分配红利。

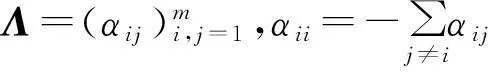
当I(t)=i时,带扰动的马氏对偶风险模型为

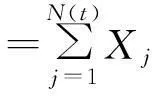
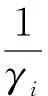
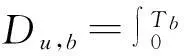
则直到破产时刻的累积分红折现期望为

其中π=(π1,π2,…,πm)是{I(t),t≥0}的初始平稳分布。

2V(u,b)满足的积分-微分方程

定理1对于u>b,累积分红折现期望V(u,b)满足下面的积分-微分方程

(1)

证明考虑很小的时间区间[0，t]，对于收益到达发生、观察分红发生和环境状态改变，有以下5种情形:

(1)在[0，t]内无观察分红，无环境状态改变，无收益到达，其概率为(1-γit-αit-λit)；

(2)在[0，t]内仅有一次观察分红，无环境状态改变，无收益到达，其概率为γit(1-αit-λit)；

(3)在[0，t]内仅有一次收益到达，无观察分红，无环境状态改变，其概率为λit(1-γit-αit)；

(4)在[0，t]内仅有环境状态改变，无观察分红，无收益到达，转移到某个状态k的概率为αikt(1-γit-λit)；

(5)在[0，t]内有两个或更多的情形发生，其概率为o(t)。

故对于u>b，有

Vi(u,b)=(1-γit-αit-λit)e-δtVi(u-cit+σiW(t),b)+

γite-δt(u-b+Vi(b,b))+λite-δt∫0+∞Vi(u-cit+σiW(t)+x,b)dFi(x)+

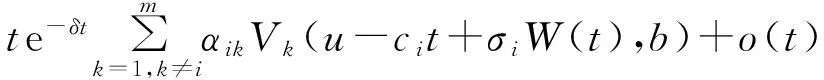
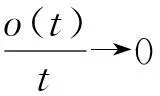
因为e-δt=1-δt+o(t)，所以有

(2)

由于

代入(2)式，两端同时除以t，并令t→0，即得(1)式，定理得证。

定理2对于0

边界条件是

证明在很小的时间区间[0，t],对于收益到达发生、观察分红发生和环境状态改变,类似定理1证明中的5种情形。但是对于情形(2)，其概率为0，因为Vi(u,b)(i=1,2)为连续函数，当0

3两状态情形下收益为指数分布时V(u,b)的解

本节我们只讨论状态m=2时的情形。假设保险公司的收益额服从指数分布，且其分布的密度函数为fi(x)=βie-βix,x>0,其中βi为环境状态为i时对应的指数分布的参数。

将fi(x)代入(1)式,化简得

对u求导，化简得

当i=1,2时，有

γ1+(γ1+δ+α1)β1V1(u,b)-γ1β1(u-b+V1(b,b))+

(3)

(4)

这两个非齐次线性微分方程的特解分别为

下面解其对应的齐次线性微分方程的解。令

方程(3)和(4)对应的齐次微分方程组可以表示为以下矩阵形式

(5)

因此矩阵C的特征多项式为

其中h(x)=h1(x)h2(x),

由上式知,矩阵C的特征多项式是六次多项式。因此假设|xI-C|=0有6个特征根,分别为ρ1,ρ2,ρ3,ρ4,ρ5,ρ6,并且每个特征根ρi所对应的特征向量设为rj,满足

因此，(5)式对应的齐次线性微分方程组的解为

其中Aj是常系数。

从而，非齐次方程(3)、(4)的解为

(6)

(7)

下面我们求解系数Aj。

由Vi(b,b),i=1,2,得

(8)

(9)

(10)

(11)

再把(6)、(7)代入(3)、(4),并且令u=b,化简得

(12)

(13)

其中

令

其中dj=eρjbrj1,ej=eρjbrj2,fj=ρjeρjbrj1,gj=ρjeρjbrj2,j=1,2,…,6。

方程组(8)—(13)可以转化为矩阵形式，即A=B-1D,这样可以确定系数Aj(j=1,2,…,6)。

4结论

在经典对偶风险模型的基础上，从实际出发，既考虑收益到达、分红和收益额大小受外部马氏环境的影响，又考虑分红在随机时间下进行，利用概率统计的相关理论，得到了累积分红折现期望V(u,b)所满足的积分-微分方程，为进一步研究其最优分红问题奠定了一定的基础。

[参考文献]

[1]Gremér H.Collective Risk Theory[M].Stockholm:Skandia Jubilee Volume,1955.

[2]ZHU Jin-xia,YANG Hai-liang.Ruin Probabilities of a Dual Markov-Modulated Risk Model[J].Communications in Statistic: Theory and Methods, 2008,37(20),3298-3307.

[3]MA Xue-min,LOU Kui,WANG Guang-ming.Constant barrier strategies in a two-state Markov-modulated dual risk model[J].Acta Math Appl Sinica,English Series,2011,24(4):679-690.

[4]ANDREW C Y Ng.On a dual model with a dividend threshold[J].Insurance Mathematics and Economics, 2009, 44(2):315-324.

[5]AVANZI B, GERBER H U, SHIU E S W.Optimal dividends in the dual model[J].Insurance Mathematics and Economics,2007,41(3):111-123.

[6]AVANZI B, GERBER H U.Optimal dividends in the dual model with diffusion[J].Astin Bulletin,2008,38(2):653-657.

[7] LU Yi.On the severity of ruin in a Markov-modulated risk model[J].Scandinavian Actuarial Journal, 2006, 2006(4):183-202.

[8]ZHU Jin-xia,YANG Hai-liang.On differentiability of ruin functions under Markov-modulated models[J].Stochastic Processes and Their Applications,2009,119(5):1673-1695.

[9]刘东海,彭丹,刘再明.常数分红界下带扰动的马氏调制对偶风险模型[J].高校应用学报,2014,29(2):159-170.

[10]AVANZI B, TU V, WONG B.On optimal periodic dividend strategies in the dual model with diffusion[J].Mathematics and Economics,2014,55(1):210-224.

[责任编辑：张存凤]

Border dividend at random observation in a type of dual risk model

ZHANG Na, WANG Xiu-lian

(College of Mathematical Science, Tianjin Normal University, Tianjin 300387, China)

Abstract:The dividends problem is one of the important issues of Finance and Insurance research. This paper considers a border strategy dividends at random observation time in a type of Markov-modulated dual risk model. We use double expectation formula to derive integral-differential equations of the expected discounted dividends until ruin time according to three factors of occurrence of income arrival process, occurrence of dividends and the change of environment state. Further more, we derive the solution of the expected discounted dividends in two state cases when the income distribution is exponential.

Key words:dual risk model;Markov-modulated process;random observation;expected discounted dividends

作者简介：张娜(1990—)，女，山西省长治市人，天津师范大学硕士研究生，主要研究方向为概率论与数理统计；[通信作者]王秀莲(1965—)，女，山西省吕梁市人，天津师范大学副教授，硕士生导师，主要研究方向为随机过程在金融保险中的应用。

基金项目：国家自然科学基金资助项目(11401436)；天津师范大学博士基金资助项目(52XB1204)

收稿日期：2015-06-04

[中图分类号]O211.67; F840

[文献标识码]A

[文章编号]1673-2944(2015)06-0073-06