基于GRA-GCRITIC和改进加权双向投影的区间Fermatean模糊多属性群决策方法

赵敬华 施佳 荣海迎 林杰

收稿日期：2023-05-29；修回日期：2023-07-27  基金項目：国家自然科学基金资助项目（72201173）；上海市“科技创新行动计划”软科学研究项目（22692108400）

作者简介：赵敬华（1984—），女，山东冠县人，副教授，硕导，博士，主要研究方向为管理决策分析、互动创新等；施佳（1999—），女（通信作者），浙江湖州人，硕士研究生，主要研究方向为决策分析（222421172@st.usst.edu.cn）；荣海迎（1997—），女，安徽怀远人，硕士研究生，主要研究方向为决策分析；林杰（1967—），男，四川渠县人，教授，博导，博士，主要研究方向为决策支持系统、供应链优化与仿真、数据挖掘等．

摘  要：针对司法案件决策环境的复杂性及评价信息的模糊性，提出一种基于GRA-GCRITIC（grey relational analysis-group criteria importance through intercriteria correlation）和改进加权双向投影的区间Fermatean模糊Hamacher-TODIM多属性群决策方法。首先考虑到各位专家对各评价方案下各指标评价信息的差异性，提出一种GRA-GCRITIC方法，该方法将灰色关联融入到CRITIC中，以确定指标综合权重比单一获取的指标权重更加客观可靠；其次，结合信任关系对加权双向投影法进行改进，兼顾主客观关系，利用专家个体与群体评价信息的隶属度及非隶属度矩阵间的相似度得到专家权重；最后，考虑到决策者的损失规避心理，将融合了Hamacher算子的TODIM方法拓展至区间Fermatean模糊环境中，通过具体算例可得到其综合优势度及排序，验证了所提方法的可行性及灵活性。

关键词：区间Fermatean模糊；GRA-GCRITIC；改进加权双向投影；Hamacher-TODIM；多属性群决策

中图分类号：C934；TP391.9    文献标志码：A

文章编号：1001-3695（2024）02-026-0493-08

doi：10.19734/j.issn.1001-3695.2023.05.0233

Interval-valued Fermatean fuzzy multi-attribute group decision-making method based on GRA-GCRITIC and improved weighted bidirectional projection

Zhao Jinghua1，Shi Jia1，Rong Haiying1，Lin Jie2

（1.School of Management，University of Shanghai for Science & Technology，Shanghai 200093，China；2.School of Economics & Management，Tongji University，Shanghai 200092，China）

Abstract：Aiming at the complexity of the judicial case decision-making environment and the fuzziness of evaluation information，this paper proposed an interval-valued Fermatean fuzzy Hamacher-TODIM multi-attribute group decision-making method based on GRA-GCRITIC and improved weighted bidirectional projection.Firstly，considering the differences in evaluation information of each index under each evaluation scheme by experts，this paper proposed a GRA-GCRITIC method，which integrated grey relation into CRITIC to determine the comprehensive weight of indicators more objectively and reliably than obtaining a single indicator weight.Secondly，considering the subjective and objective relationship，this paper used the trust relationship to improve the weighted bidirectional projection method.The approach utilized the similarity between the membership and non-membership degree matrices of expert individual and group evaluation information to obtain expert weights.Finally，considering the decision-makers loss aversion psychology，this paper extended the TODIM method，which incorporated the Hamacher operator，to an interval-valued Fermatean fuzzy environment.And a specific case used this method to obtain the comprehensive advantage and ranking.It verifies the feasibility and flexibility of the proposed method.

Key words：interval-valued Fermatean fuzzy；GRA-GCRITIC；improved weighted bidirectional projection；Hamacher-TODIM；multi-attribute group decision-making

0  引言

近年來，司法舆情案件的相关话题易引起社会高度关注，而社会舆论一定程度上也会使该类案件陷入“执行难”的困境，以至于影响社会法治化进程［1］。因此，诸多学者对其进行研究。王新雷等人［2］通过分析220件涉人工智能案件的裁判结果，指出现阶段该类案件在法律适用方面存在的突出难题；白梅［3］针对民间借贷案件执行难问题，指出各部门各组织需增强协作配合，强化执行措施等，以确保案件执行难的问题标本兼治。在现有研究成果中，主要体现在案件执行难的困境描述以及给出相应的解决措施， 较少采用科学的决策方法对司法案件进行综合评价。考虑到司法领域的复杂性、不确定性，以及单人决策的局限性，专家群体在评价司法案件时会涉及到多方面因素，可将其视为一个多属性群决策问题。

专家群体由于自身知识水平、经验等差异性难以对复杂的司法案件作出准确评价，往往以模糊数的形式表达自身偏好。为了使评价信息表达方式更全面有效，学者不断拓展模糊集的相关研究，Senapati等人［4］将隶属度与非隶属度范围扩充至0≤μ3+v3≤1 ，提出了Fermatean模糊集（FFS）；Jeevaraj［5］在FFS基础之上，提出区间Fermatean模糊集（IVFFS），以［0，1］中的闭合子区间来刻画隶属度和非隶属度，从而更为灵活高效地度量不确定信息。关于IVFFS已有较多的研究成果，譬如Jeevaraj［5］提出了距离测度、相似测度和得分函数、精确函数等；Rani等人［6］在此基础上提出了改进得分函数并验证其有效性。集成算子在多属性群决策过程中起到聚合专家群体评价值的作用，除了最常见的加权平均、几何算子以外，Einstein算子［6］、Hamacher算子［7］、Frank算子［8］等也在逐步应用至IVFFS中。IVFFS常用的决策方法有TOPSIS［6］、COPRAS［9］等，但考虑决策者损失规避心理的TODIM方法鲜有研究。同时，现有文献中TODIM模糊评价方法仍存在不足，学者主要将其应用于最终评价结果［10］，而忽略了聚合信息过程中决策者的心理行为，即结合集成算子的TODIM法有待深入探究。

在实际进行决策时，属性间往往存在一定的联系。譬如司法案件的执行时间长短会在一定程度上体现出其执行机制是否合理，也会影响到其法律效应和社会效应，而执行质量的结果也会从中有所凸显。相反，案件的执行程序是否得当等诸多因素也会对执行时间有所影响。CRITIC法是以标准差和线性相关系数来衡量属性间的差异和关联［11］，诸多学者将该方法与改进得分函数［6］、距离相关性［12］、CODAS-SORT法［13］、TOPSIS法［14］等相融合，从而获取影响决策的多维属性权重。但属性间的关联不一定是线性关系，通常存在非线性关系。灰色关联（GRA）的基本思想是以序列曲线几何形状的逼近程度来判断其联系是否紧密，若曲线越接近，相应的序列之间关联度就越大，反之就越小［15］。灰关联度能更加灵活地反映属性间的非线性关系，进而得到属性权重信息。张识宇等人［15］将CRITIC法和灰关联度结合应用于精确数的评价环境中，获取组合权重。然而，区间Fermatean模糊集灰关联度的研究鲜有文献发表。

若片面地由某位专家对司法案件进行主观评价，这可能很难达成专家群体共识，因此采用专家群体智慧进行综合评价的方法会显得更加客观可靠。而专家群体往往具备不同的决策能力，选择合适的专家权重确定方法有利于完善多属性群决策体系。现阶段基于区间Fermatean模糊环境的多属性群决策中，学者往往直接根据专家影响力或专家间的信任程度［8］主观赋予专家权重，鲜有学者对其进行深入探究，仅发现文献［7］提出了一个专门用来确定专家权重的公式，以及文献［16］基于前景理论获得专家前景权重。但在其他模糊环境下，学者常根据客观评价信息来确定专家权重，梁薇等人［17］在基本不确定区间犹豫模糊环境下，提出了基于可信度的专家权重确定方法；杜秀丽等人［18］将加权双向投影法引入到区间直觉模糊环境中，通过专家与群体间的偏好相似度来确定专家权重；赵敬华等人［19］在毕达哥拉斯模糊环境中融合了信任网络和偏好相似度，综合主客观因素以获得专家权重，并将其应用到应急群决策中。

经上述文献梳理可知，区间Fermatean模糊环境下的决策方法仍较少，还未涉及到考虑决策者损失规避心理行为的TODIM方法，且现阶段TODIM方法缺少与集成算子的结合。同时现有研究成果主要集中在供应商的选择、新能源汽车充电桩的选址、应急决策等领域，但对于司法案件评价背景下的多属性群决策方法的研究较少。目前未见学者将GRA与CRITIC方法结合应用于区间Fermatean模糊环境中的属性权重确定；且关于专家权重的研究还有待拓展。鉴于此，本文提出一种基于GRA-GCRITIC和改进加权双向投影的区间Fermatean模糊Hamacher-TODIM多属性群决策方法，并将该方法应用于司法案件评价中。

1  预备知识

定义1［3］  设X为论域，则该论域上的Fermatean模糊集（FFS）可表示为

F={〈x，μF（x），νF（x）〉|x∈X}（1）

其中：X→［0，1］，x∈X；μF（x）∈［0，1］代表元素x属于X的隶属度；νF（x）∈［0，1］，代表元素x属于X的非隶属度，且对于任意x∈X，0<（μF（x））3+（νF（x））3≤1；犹豫度或不确定度πF（x）=31-（μF（x））3-（νF（x））3。

定義2［5］  设X为论域，则该论域上区间Fermatean模糊集（IVFFS）可表示为

F={〈x，［μFL（x），μFU（x）］，［νFL（x），νFU（x）〉|x∈X}（2）

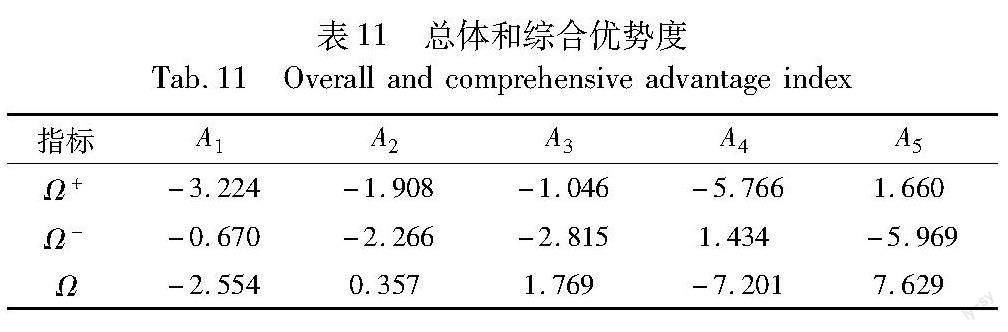
其中：X→Int［0，1］，x∈X；μF（x）=［μFL（x），μFU（x）］代表元素x属于X的隶属度；νF（x）=［νFL（x），νFU（x）］ 代表元素x属于X的非隶属度，且对于任意x∈X，0

定义3［5］  若F=〈［μFL，μFU］，［νFL，νFU］〉，F1=〈［μF1L，μF1U］，［νF1L，νF1U］〉和F2=〈［μF2L，μF2U］，［νF2L，νF2U］〉为三个区间Fermatean模糊数，且λ>0 ，则有如下运算法则：

a） F1F2=［3μF1L3+μF2L3-μF1L3μF2L3，

3μF1U3+μF2U3-μF1U3μF2U3］，［νF1LνF2L，νF1UνF2U］；

b） F1F2=［μF1LμF2L，μF1UμF2U］，

［3νF1L3+νF2L3-νF1L3νF2L3，3νF1U3+νF2U3-νF1U3νF2U3］；

c） λF=［31-（1-μFL3）λ，31-（1-μFU3）λ］，［νFLλ，νFUλ］；

d） Fλ=［μFLλ，μFUλ］，［31-（1-νFL3）λ，31-（1-νFU3）λ］。

定义4［5］  设F=〈［μFL，μFU］，［νFL，νFU］〉为区间Fermatean模糊数，则F的得分函数为

S（F）=12（（μFL）3+（μFU）3-（νFL）3-（νFU）3）∈［-1，1］（3）

式（3）是最常用的得分函数，但其未考虑犹豫度，在一些特殊情况下可能会失效，例如：对于两个IVFFN，F1=（［30.25，30.3］，［30.35，30.5］），F2=（［30.15，30.4］，［30.25，30.6］）运用式（3）无法区别两者大小，但其犹豫度显然不同。因此，本文采用文献［6］提出的区间Fermatean模糊改进得分函数（F） 。

定义5［6］  设F=〈［μFL，μFU］，［νFL，νFU］〉为区间Fermatean模糊数，则F的得分函数为

（F）=12（（（μFL）3-（νFL）3）（1+πFU）+（（μFU）3-（νFU）3）（1+πFL））∈［-1，1］（4）

接上例，运用式（4）比较F1和F2，可以得到S（F1）=-0.245

定义6［5］  设F1=〈［μF1L，μF1U］，［νF1L，νF1U］〉，F2=〈［μF2L，μF2U］，［νF2L，νF2U］〉为两个区间Fermatean模糊数，则F1和F2的欧氏距离为

D（F1，F2）=16（μ3F1L-μ3F2L）2+（μ3F1U-μ3F2U）2+（ν3F1L-ν3F2L）2+

（ν3F1U-ν3F2U）2+（π3F1L-π3F2L）2+（π3F1U-π3F2U）2（5）

定理1［7］  设Fi=〈［μFiL，μFiU］，［νFiL，νFiU］〉（i=1，2，…，n）为一组区间Fermatean模糊数，η>0，w=（w1，w2，…，wn）T是其权重向量，wi≥0，i=1，2，…，n，∑ni=1wi=1，则区间Fermatean模糊Hamacher加权平均算子，即

IVFFHWA（F1，F2，…，Fn）=⊕ni=1（wi·Fi）=

3ni=1（1+（η-1）·μFiL3）wi-ni=1（1-μFiL3）wini=1（1+（η-1）·μFiL3）wi+（η-1）ni=1（1-μFiL3）wi，

3ni=1（1+（η-1）·μFiU3）wi-ni=1（1-μFiU3）wini=1（1+（η-1）·μFiU3）wi+（η-1）ni=1（1-μFiU3）wi，

3ηni=1（vFiL）wi3ni=1（1+（η-1）（1-vFiL3））wi+（η-1）ni=1（vFiL）3wi，

3ηni=1（vFiU）wi3ni=1（1+（η-1）（1-vFiU3））wi+（η-1）ni=1（vFiU）3wi（6）

定理2［7］  设Fi=〈［μFiL，μFiU］，［νFiL，νFiU］〉（i=1，2，…，n）为一组区间Fermatean模糊数，η>0，w=（w1，w2，…，wn）T是其权重向量，wi≥0，i=1，2，…，n；∑ni=1wi=1，则区间Fermatean模糊Hamacher加权几何算子，即

IVFFHWG（F1，F2，…，Fn）=ni=1（Fi）wi=

3ηni=1（μFiL）wi3ni=1（1+（η-1）（1-μFiL3））wi+（η-1）ni=1（μFiL）3wi，

3ηni=1（μFiU）wi3ni=1（1+（η-1）（1-μFiU3））wi+（η-1）ni=1（μFiU）3wi，

3ni=1（1+（η-1）·νFiL3）wi-ni=1（1-νFiL3）wini=1（1+（η-1）·νFiL3）wi+（η-1）ni=1（1-νFiL3）wi，

3ni=1（1+（η-1）·νFiU3）wi-ni=1（1-νFiU3）wini=1（1+（η-1）·νFiU3）wi+（η-1）ni=1（1-νFiU3）wi（7）

2  GRA-GCRITIC和改进加权双向投影法的构建

对于一个属性值为区间Fermatean模糊语言的多属性群决策问题，设专家群体集合为E={e1，e2，…，ek}，被评价方案集合为A={A1，A2，…，Am}，评价指标集合为C={c1，c2，…，cn}。评价矩阵Xl =［xlij］m×n表示第l位专家对第i个评价方案的第j个指标的评价信息值（1≤l≤k，1≤i≤m，1≤j≤n）。

2.1  基于GRA-GCRITIC的指标权重确定方法

在多属性群决策过程中，各位专家对各评价方案下的各指标评价信息往往存在差异，且不同指标之间必然会存在一定的关联。CRITIC法是一种兼顾评价指标信息差异和关联的属性赋权方法，但它存在一定的局限性。而灰色关联能更灵活地反映指标间的非线性关系，可有效弥补CRITIC中线性相关系数的缺陷。本文参考文献［15］，提出一种GRA-GCRITIC方法，该方法在CRITIC基础上改线性相关系数为灰色综合关联度，能以系统的角度反映区间Fermatean模糊环境多属性群决策问题中多维指标间的关联性，同时依靠专家群体来确定指标综合权重比单一获取的指标权重更加客观可靠。其主要步骤如下：

a）专家群体给出各自的评价信息。专家el根据自身经验给出相应的区间Fermatean模糊初始评价矩阵Xl=［xlij］m×n，其中xlij=（［μFLijl，μFUijl］，［νFLijl，νFUijl］）。

Xl=xl11xl21…xl1n

xl21xl22…xl2n

xlm1xlm2…xlmnm×n

b）规范化评价矩阵。为了消除成本型和效益型指标之间的差异，通过规范化各评价指标，得到规范化评价矩阵l=［lij］m×n，其中

l ij =（［lFLij，lFUij］，［lFLij，lFUij］）=

（μFLijl，μFUijl］，［νFLijl，νFUijl］）cj属于效益型指标

（［νFLijl，νFUijl］，μFLijl，[μFUijl］）cj属于成本型指标（8）

c）计算得分函数矩阵。根据改进得分函数式（4），将规范化评价矩阵l=［ijl］m×n转换为得分函数矩阵l=［lij］m×n。

d）根据得分函数矩阵，计算指标的标准差，以衡量指标间的纵向差异性。

σlj=∑mi=1（lij-lj）2m（9）

其中：lj=∑mi=1lij/m。

e）根据得分函数矩阵，计算各指标的灰色最优关联度rljmax、最劣关联度rljmin及综合关联度Rlj，以衡量指标间的横向相似性。

rlj max=1m∑mi=1mini minj|l+j-lij|+ζ maxi maxj|l+j-lij||l+j-lij|+ζ maxi maxj|l+j-lij|（10）

rlj min=1m∑mi=1mini minj|lij-l-j|+ζ maxi maxj|lij-l-j||lij-l-j|+ζ maxi maxj|lij -l-j|（11）

Rlj=1（1+rlj minrlj max）（12）

其中：jl+=maxmi=1 ijl，jl-=minmi=1ijl；ζ是分辨系数，ζ∈［0，1］，一般取ζ=0.5。

f） 计算各专家对不同指标的优先级权重：

Zlj=σlj×Rlj（13）

进行归一化处理得到各专家对不同指标的权重值：

wlj=Zlj/∑nj=1Zlj（14）

其中：wlj∈（0，1），且∑nj=1wlj=1。

g） 计算专家群体的指标综合权重：

Wj=∑kl=1wlj×wel（15）

其中：wel表示第l位专家的最终权重，将在2.2节中详细阐述。Wj∈（0，1），且∑nj=1Wj=1。

2.2  结合信任关系的改进加权双向投影法的专家权重确定

在实际决策过程中，确定合理的专家权重对评价结果的准确性和公正性至关重要。专家权重的确定需要综合考虑多方面因素，包括专家的经验水平、专业背景、专家间的信任关系等主观因素，以及个人评价信息与群体综合评价信息间的相似度等客观因素。

2.2.1  专家初始权重的构建

为了准确度量专家个体在决策过程中的影响力，可以根据专家间的信任关系来确定其初始权重。专家通常采用“非常信任”“较信任”“一般信任”等语言术语表达对他人的信任程度，故本文结合语言术语来表示专家间的信任关系。

定义7［20］  专家es对eh的信任关系可以用语言术语lshα（α=-τ，-τ+1，…，0，…，τ-1，τ）表示，如表1所示。

其中：lshα代表專家es对eh 的信任关系用语言术语lα表示时的下标α（s，h∈k，s≠h）。参照文献［8］，将语言术语定量化，专家es对eh的信任程度如下所示。

tsh=lshα+τ2τ（16）

根据信任程度可进一步获得专家eh的初始权重：

Eeh=∑ks=1，s≠htsh/∑kh=1  ∑ks=1，s≠htsh（17）

其中：Eeh∈（0，1），且∑kh=1Eeh=1。

2.2.2  利用改进加权双向投影法求取专家最终权重

鉴于区间Fermatean模糊评价信息之间相似测度的局限性，本文参考文献［18］提出的改进加权双向投影方法，将每位专家的评价矩阵和聚合后的综合评价矩阵划分成隶属度矩阵和非隶属度矩阵，由这两种矩阵分别得到双向投影值，并将其加权融合求出专家个体与群体间的相似度，从而求取专家最终权重。其主要步骤如下：

a） 专家聚合评价信息。根据Hamacher算子式（6）（7）以及专家初始权重Eel聚合各专家的初始规范化评价矩阵，从而获得初始综合评价矩阵=［ij］m×n，其中ij=（［FLij，FUij］，［FLij，FUij］）。

b） 划分得到隶属度矩阵及非隶属度矩阵。根据隶属度及非隶属度对各专家的初始规范化评价矩阵Xl=［xijl］m×n和初始综合评价矩阵=［ij］m×n进行划分，可以得到专家el评价信息的隶属度矩阵Pl =（μlFij）m×n=（［μlFLij，μlFUij］）m×n、非隶属度矩阵Ql =（νlFij）m×n=（［νlFLij，νlFUij］）m×n；初始综合评价信息的隶属度矩阵=（Fij）m×n=（［FLij，FUij］）m×n、非隶属度矩阵=（Fij）m×n=（［FLij，FUij］）m×n。

c）计算加权双向投影值。考虑到不同指标的权重wlj对矩阵相似性的影响，在步骤b） 基础之上，求得专家el评价信息和初始综合评价信息的隶属度矩阵、非隶属度矩阵的加权双向投影值。以隶属度矩阵为例：

WBP（Pl，）=11+|Plw‖Plw‖-Plw‖w‖|（18）

其中：

‖Plw‖=∑mi=1∑nj=1（wlj）2（（μFLijl）2+（μFUijl）2）（19）

‖w‖=∑mi=1∑nj=1（wlj）2（2FLij+2FUij）（20）

Pl w=∑mi=1  ∑nj=1（wlj）2μlFijFij=∑mi=1  ∑nj=1（wlj）2（μlFLijFLij+μlFUijFUij）（21）

同理，可求得WBP（Ql，Q^），不再贅述。

d） 计算专家el与群体相似度。

Dl（φ）=φWBP（Pl，）+（1-φ）WBP（Ql，Q^）（22）

其中：φ为隶属度和非隶属度偏好系数，φ∈［0，1］。

e） 求取专家最终权重。专家与群体的相似度越大，则该专家被赋予较大权重。反之，该专家被赋予较小权重。

wel=Dl（φ）∑kl=1Dl（φ）（23）

其中：wel∈（0，1），且∑kl=1wel=1。

3  基于GRA-GCRITIC和改进加权双向投影的Hamacher-TODIM群决策模型

为了更好地处理评价信息的模糊性和复杂性，本文在区间Fermatean模糊环境中引入了GRA-GCRITIC方法求取各专家对不同指标的权重wlj，在由信任关系得到的专家初始权重Eel基础上改进加权双向投影法，进一步求得专家最终权重wel；同时考虑到专家的损失规避心理行为，将结合了Hamacher算子的TODIM方法应用于区间Fermatean模糊多属性群决策问题中。具体步骤如下：

a）根据改进得分函数将各专家给出的评价矩阵转换成得分函数矩阵Sl=［sijl］m×n，计算各指标的标准差σlj和灰色综合关联度Rlj，从而求得各专家对不同指标的权重值wlj。

b）通过信任关系得到专家初始权重Eel后，采用Hamacher算子进行聚合获得初始综合评价矩阵；在专家el评价信息和初始综合评价信息的隶属度矩阵Pl =（μlFij）m×n、=（Fij）m×n，非隶属度矩阵Ql =（νlFij）m×n、=（Fij）m×n基础之上，计算加权双向投影值WBP（Pl，）、WBP（Ql，），进而求出专家el与群体相似度Dl（φ），确定专家最终权重wel。

c）求得专家最终权重wel后，再次利用Hamacher算子进行聚合获得最终综合评价矩阵′=［′ij］m×n，其中′ij=（［′FLij，′FUij］，［′FLij，′FUij］）。

d）根据式（15）确定专家群体的指标综合权重，并进一步计算各指标的相对权重：

Wjr=Wj/Wr（24）

其中：Wr=maxnj=1 Wj。

e） 计算指标Cj下，方案As相较于方案At的优势度：

Φj（As，At）=wjr∑nj=1wjrD（′sj，′tj）′sj′tj

0′sj～′tj

-1θ∑nj=1wjrwjrD（′sj，′tj）′sj′tj（25）

其中：D（′sj，′tj）表示IVFFN间的距离，可由式（5）计算得到；θ表示专家面对损失时的风险因子，且θ>0（1≤s≤m，1≤t≤m，s≠t）。

f） 计算方案As相较于其他方案的总体优势度，其他方案相较于方案As的总体优势度以及方案As的综合优势度：

Ω+（As，At）=∑mt=1∑nj=1Φj（As，At）（26）

Ω-（At，As）=∑mt=1∑nj=1Φj（At，As）（27）

Ω（As）=Ω+（As，At）-Ω-（At，As）（28）

g） 对方案的综合优势度进行排序，得到最佳和最劣方案。

4  算例分析

由于司法案件的复杂性和不确定性，司法机关在短时间内很难对其作出准确的判断。通过对司法案件进行科学评价，挑选出典型案件，进而可以通过媒体等渠道进行宣传，提高法律的知名度和公信力，推动社会法制化进程。同时，这些典型案件可以作为其他司法机关学习和参考的案例，有助于提高司法机关的执行效率和质量，推动司法工作的规范化、专业化和现代化。此外，评选典型案件有利于发现执行过程中存在的问题和不足，为推进司法改革和创新提供借鉴价值，有助于建立更加完善和先进的司法制度和执行机制。因此，构建科学合理的司法案件评价方法，是司法机关提高执行能力和水平的重要手段，也是促进司法公正、推动社会发展进步的力量源泉。

现邀请五位司法领域专业人士E={e1，e2，e3，e4，e5} 参考一系列典型司法案件归纳出最为重要的五项指标C={C1，C2，C3，C4，C5}，如表2所示，并对五个备选司法案件A={A1，A2，A3，A4，A5}进行评价，专家以区间Fermatean模糊数的形式给出相应的评价信息。下面利用基于GRA-GCRITIC和改进加权双向投影法的Hamacher-TODIM群决策方法来评出最具代表性的司法案件。

4.1  基于GRA-GCRITIC方法的指标权重

五位专家分别对五个备选案件的五项指标进行评价，得到区间Fermatean模糊初始评价矩阵Xl=［xlij］m×n，并根据式（8）将其规范化，得到规范化评价矩阵Xl=［xijl］m×n，如表3所示。利用改进得分函数式（4），将规范化评价矩阵转换成得分函数矩阵Sl=［sijl］m×n；再根据式（9）～（12）求得各专家关于指标间的标准差σlj和灰色综合关联度Rlj，如表4、5所示。通过式（13）（14）求得各专家对不同指标的权重值wlj，如表6所示。

对表6进行分析，发现专家e1、e2、e4、e5均认为指标C5（案件的执行质量）相对最重要，专家e3也将指标C5认定为次重要指标，可见其影响程度相对较高。专家e2、e3、e5均认为指标C1（案件的执行时间）相对最不重要，专家e1也将指标C1认定为次不重要指标，说明该指标在整体中的影響程度相对较低。

4.2  结合信任关系的改进加权双向投影法的专家权重

具有不同经验、知识水平的专家以语言数形式表达自己对其他专家的信任关系，获得专家群体的信任关系矩阵，如表7所示。参照文献［8］，取τ=4。通过式（16）可将信任关系转换为信任程度，并进一步利用式（17）得到专家初始权重Eel=（0.165，0.212，0.153，0.200，0.271）。

获得专家初始权重后，利用IVFFHWA算子式（6）对各专家的初始规范化评价矩阵（表3）进行聚合，得到初始综合评价矩阵，如表8所示。为保证数据客观性，取η=1。在此基础上，根据式（18）～（21）可得专家个体评价信息与综合评价信息的隶属度矩阵、非隶属度矩阵之间的加权双向投影值WBP（Pl，）、WBP（Ql，），并通过式（22）得到专家el与群体相似度Dl（φ），如表9所示。为保证权重的合理性，取偏好系数φ=0.5。最后，利用式（23）可以求得专家最终权重wel=（0.201，0.203，0.185，0.200，0.210）。这说明第五位专家在司法案件评选中的评价最为重要，不仅仅是因为其在专业领域的影响力，更是因为其在司法案件的评选中始终能与群体中其他专家达成共识。

4.3  Hamacher-TODIM决策方法

根据已得专家最终权重wel，再次利用IVFFHWA算子式（6）对初始规范化评价矩阵（表3）进行聚合，得到最终综合评价矩阵，如表10所示。同时，利用式（15）可得到专家群体的指标综合权重Wj=（0.147，0.182，0.197，0.203，0.272），进一步通过式（24） 可求得指标相对权重。

获得指标相对权重后，利用式（4）（5）（25）～（28）可以计算出备选司法案件的优势度、总体优势度及综合优势度，如表11所示。不失一般性，取θ=2.25。根据综合优势度对备选司法案件进行降序排列，得出A5A3A2A1A4，即第五个司法案件最具有代表性和权威性，而第四个司法案件的评价结果最劣。

为进一步加深对司法案件“执行难”的认识，对以上五个备选司法案件的综合评价结果进行分析。第五个司法案件在各项指标下的执行均较好，但对于“执行机制”这一指标层面需要加强，其面对复杂或特殊情况时的执行能力需进一步提升；第三个司法案件要提高创新意识和执行质量，在面对难办案件时，创新意识尤为重要，所以在执行机制方面须及时进行改革创新以促进案件的顺利执行；第二个司法案件产生的舆论易对社会行为和公共秩序产生影响，所以要及时作出执行措施，以改善社会效果；第一个案件中的司法部门按照已有法律规定处理该案件时所产生的法律效应不佳，需及时审查核实案件证据是否全面、应用法律是否准确、法律文书是否规范等；第四个司法案件虽在“执行质量”这一指标表现尚可，但在其余四项指标下均表现不佳，由于各项指标的综合权重相差不大，故该案件综合评价最劣。

5  对比分析

5.1  Hamacher集成算子和TODIM方法分析

Hamacher算子［21］是一种灵活、可解释的模糊集合集成算子，它可以将不同的模糊信息聚合为更全面准确的信息，同时它的调节因子可以根据不同的决策背景来调整聚合程度，为高效决策提供了更大的发展空间。利用文献［7］基于区间Fermatean模糊Hamacher集成算子的方法对上述问题直接进行求解，如表12所示，可以发现基于IVFFHWA算子和IVFFHWG算子得到的排序结果最优方案均是A5，最劣方案均是A4，这说明Hamacher集成算子具有一定的鲁棒性，能够在一定程度上减小随机误差等对聚合结果的影响，使得决策结果更加实用可靠。

在传统的TODIM方法中，决策者的损失规避心理行为是重要考虑因素，它通常结合普通的算子求取各方案的综合优势度并对其进行排序。但是当两个模糊集合的交集为空集时，普通的算子可能无法处理这种情况。考虑到司法案件的群决策问题涉及到广泛的决策背景和诸多社会因素，指标属性值存在较大不确定性，仅靠普通的集成算子聚合会出现不合理的结果。本文Hamacher-TODIM决策方法不仅利用良好算子进行信息集成，提高了决策效率，而且充分考虑决策者的损失规避心理特征，具有一定的准确性和可靠性，这对于复杂的司法案件决策来说具有重要意义。

5.2  前景理论和改进得分函数分析

为了凸显本文基于GRA-GCRITIC和改进加权双向投影的Hamacher-TODIM决策方法的合理性和有效性，使用文献［16］基于前景理论的区间Fermatean模糊环境对上述问题进行求解，得到的排序结果为A5A3A2A1A4 ，总体排序与本文一致。在利用前景理论计算备选司法案件的前景值时，首先需要设定前景参照点，且参照点的设定存在主观误差，而TODIM方法是在前景理论基础上提出来的［22］，无须选取参照点，这也说明了TODIM方法具有一定的优越性。

使用文献［5］的得分函数和区间Fermatean模糊加权Hamacher算子对上述问题进行求解，可以发现其得分函数的总体排序与本文的改进得分函数基本完全一致，如图1所示，但文献［5］的得分函数未考虑犹豫度，使得在求解过程中一些备选司法案件间的得分函数过于接近，从而导致选择失效，这说明改进得分函数可以明显区分出最优最劣司法案件，具有较高的准确性。

5.3  灵敏性分析

在改进加权双向投影法的构建中，为了了解隶属度和非隶属度偏好系数φ对方案排序产生的影响，对其进行敏感性分析。φ∈［0，1］时，备选司法案件的综合优势度如图2所示，可见无论隶属度和非隶属度偏好系数的取值如何变化，对最终排序无影响。 φ=0 时专家完全根据非隶属度相似度取得专家最终权重；φ=1时专家完全根据隶属度相似度取得专家最终权重，这也说明了该方法具有稳定性。

在基于区间Fermatean模糊加权Hamacher算子的TODIM方法决策过程中，风险因子θ可以反映专家的损失规避心理行为，故对其进行灵敏性分析。取θ∈［0.25，2.25］，研究其对备选司法案件的综合优势度及排序的影响，如图3所示，可见风险因子θ的取值不会对最终排序造成影响。但当风险因子θ=0.25时，各司法案件综合优势度的区分度极大，专家受损失的影响相对最大；反之，当风险因子θ=2.25时，各司法案件综合优势度的区分度最小，专家受损失的影响也相对最小。随着θ的增大，司法案件的最劣综合优势度呈上升趋势，最优综合优势度呈下降趋势。

6  结束语

针对司法案件“执行难”决策背景，利用区间Fermatean模糊环境对其进行研究，本文提出了基于GRA-GCRITIC和改进加权双向投影的Hamacher-TODIM决策方法，所提方法创新点如下：

a）区间Fermatean模糊环境可以更全面地涵盖不确定性信息，同时提高了专家个体表达方式及偏好的灵活性。

b）提出GRA-GCRITIC方法分别确定各位专家对各评价方案下各指标的权重，并结合专家权重获得指标综合权重比单一获取的指标权重更加客观可靠。

c）针对群决策中专家权重未知，在信任关系基础上提出改进加权双向投影法得到专家最终权重，全面反映出专家群体的主客观因素，提高了群决策的评价效率。

d）Hamacher算子和TODIM方法分别考虑了指标属性值的灵活多样性和专家群体的损失规避心理行为，将两者有效融合能使决策结果更切合实际。

最后通过专家群体评价备选司法案件验证了该决策方法的可行性和稳定性，为区间Fermatean模糊多属性群决策问题开拓新思路。且TODIM方法结合了良好集成算子的灵活性和鲁棒性，对于司法领域决策问题具有一定的实践意义。

由于现实环境的不确定性和社会性，专家群体间、指标属性间的相互关系错综复杂，而复杂网络中的不同网络属性从不同角度描述了不同节点的重要性［23］，所以下一步的研究方向是将复杂网络融入到该决策方法中，从而获取专家权重和属性权重信息。同时考虑到评价信息的多樣性，仅靠区间Fermatean模糊数来进行评价存在不足，故可以将其与概率语言环境进一步融合。

参考文献：

［1］何士青，赵佳敏.隐蔽区隔：基于网络司法舆情的考辩［J］.情报杂志，2019，38（6）：102-109，94.（He Shiqing，Zhao Jiaming.Concealed interval：based on Internet justice of public opinion［J］.Journal of Intelligence，2019，38（6）：102-109，94.）

［2］王新雷，秦文豪.涉人工智能案件的审判难点及应对思路—基于对220件司法裁判结果的实证研究［J］.北京航空航天大学学报：社会科学版，2023，36（6）：45-56.（Wang Xinlei，Qin Wenhao.Trial difficulties and countermeasures of cases involving artificial intelligence：an empirical study based on the results of 220 judicial decisions［J］.Journal of Beijing University of Aeronautics and Astronautics：Social Sciences Edition，2023，36（6）：45-56.）

［3］白梅.民间借贷案件执行难问题的解决对策［J］.人民论坛，2021，705（14）：87-89.（Bai Mei.Solutions to the difficulty in executing private loan cases［J］.Peoples Tribune，2021，705（14）：87-89.）

［4］Senapati T，Yager R R.Fermatean fuzzy weighted averaging/geometric operators and its application in multi-criteria decision-making methods［J］.Engineering Applications of Artificial Intelligence，2019，85：112-121.

［5］Jeevaraj S.Ordering of interval-valued Fermatean fuzzy sets and its applications［J］.Expert Systems with Applications，2021，185：article ID 115613.

［6］Rani P，Mishra A R，Deveci M，et al.New complex proportional assessment approach using Einstein aggregation operators and improved score function for interval-valued Fermatean fuzzy sets［J］.Compu-ters & Industrial Engineering，2022，169：article ID 108165.

［7］Deveci M，Gokasar I，Mishra A R，et al.Evaluation of climate change-resilient transportation alternatives using fuzzy Hamacher aggregation operators based group decision-making model［J］.Engineering Applications of Artificial Intelligence，2023，119：article ID 105824.

［8］曾守桢，顾佳星，叶军.复杂信任网络群组综合评价方法及应用研究［J］.商业经济与管理，2022，42（11）：84-100.（Zeng Shouzhen，Gu Jiaxing，Ye Jun.Research on group comprehensive evaluation method of complex trust network and its application［J］.Journal of Business Economics，2022，42（11）：84-100.）

［9］Mishra A R，Liu Peide，Rani P.COPRAS method based on interval-valued hesitant Fermatean fuzzy sets and its application in selecting desalination technology［J］.Applied Soft Computing，2022，119：article ID 108570.

［10］Tian Xiaoli，Li Wanqing，Liu Li，et al.Development of TODIM with different types of fuzzy sets：a state-of the-art survey［J］.Applied Soft Computing，2021，111：article ID 107661.

［11］Mishra A R，Chen Shiming，Rani P.Multicriteria decision making based on novel score function of Fermatean fuzzy numbers，the CRITIC method，and the GLDS method［J］.Information Sciences，2023，623：915-931.

［12］Sharkasi N，Rezakhah S.A modified CRITIC with a reference point based on fuzzy logic and hamming distance［J］.Knowledge-Based Systems，2022，255：article ID 109768.

［13］Aro J L，Selerio E，Evangelista S S，et al.Fermatean fuzzy CRITIC-CODAS-SORT for characterizing the challenges of circular public sector supply chains［J］.Operations Research Perspectives，2022，9：article ID 100246.

［14］Saxena P，Kumar V，Ram M.A novel CRITIC-TOPSIS approach for optimal selection of software reliability growth model（SRGM）［J］.Quality and Reliability Engineering International，2022，38（5）：2501-2520.

［15］張识宇，杨凯悦，刘书龙.基于改进CRITIC权重法的民营科技孵化器绩效组合评价方法［J］.科技管理研究，2022，42（17）：57-64.（Zhang Shiyu，Yang Kaiyue，Liu Shulong.Combination evaluation on private technology incubator performance based on refined CRITIC［J］.Science and Technology Management Research，2022，42（17）：57-64.）

［16］罗世华，刘俊.拓展区间Fermatean模糊前景理论综合评价方法［J/OL］.中国管理科学.（2023-04-11）［2023-07-25］.https：//doi.org/10.16381/j.cnki.issn1003-207x.2022.0663.（Luo Shihua，Liu Jun.A comprehensive evaluation method based on extended interval-valued Fermatean fuzzy prospect theory［J/OL］.Chinese Journal of Management Science.（2023-04-11）［2023-07-25］.https：//doi.org/10.16381/j.cnki.issn1003-207x.2022.0663.）

［17］梁薇，王应明.基于可信度的基本不确定区间犹豫模糊广义TODIM应急群决策方法［J］.控制与决策，2023，38（7）：1988-1996.（Liang Wei，Wang Yingming.Generalized TODIM emergency group decision making method for basic uncertain information interval-valued hesitant fuzzy set based on reliability degree［J］.Control and Decision，2023，38（7）：1988-1996.）

［18］杜秀丽，聂彦刚，吕亚娜，等.基于加权双向投影的决策专家权重确定方法［J］.控制工程，2023，30（1）：83-89.（Du Xiuli，Nie Yangang，Lyu Yana，et al.A method to determine weight of decision experts based on weighted bidirectional projection［J］.Control Engineering of China，2023，30（1）：83-89.）

［19］赵敬华，荣海迎，吕锡婷，等.基于DEMATEL和信任网络的毕达哥拉斯模糊多属性应急决策方法［J］.计算机应用研究，2023，40（1）：165-171.（Zhao Jinghua，Rong Haiying，Lyu Xiting，et al.Pythagorean fuzzy multi-attribute emergency decision-making method based on DEMATEL and trust network［J］.Application Research of Computers，2023，40（1）：165-171.）

［20］王偉明，徐海燕，朱建军.基于复杂网络和语言信息的交互式大规模群体评价方法［J］.中国管理科学，2022，30（11）：260-271.（Wang Weiming，Xu Haiyan，Zhu Jianjun.Interactive large-scale group evaluation method based on complex network and linguistic information［J］.Chinese Journal of Management Science，2022，30（11）：260-271.）

［21］刘卫锋，常娟，何霞.毕达哥拉斯模糊Hamacher集成算子及其决策应用［J］.系统工程理论与实践，2018，38（6）：1566-1574.（Liu Weifeng，Chang Juan，He Xia.Pythagorean fuzzy Hamacher aggregation operators and its application to decision making［J］.Systems Engineering-Theory & Practice，2018，38（6）：1566-1574.）

［22］Tian Xiaoli，Ma Jiangshui，Li Liu，et al.Development of prospect theory in decision making with different types of fuzzy sets：a state-of-the-art literature review［J］.Information Sciences，2022，615：504-528.

［23］赵敬华，张艳，张维，等.基于异质信息的被执行人的评估决策问题研究［J］.控制与决策，2023，38（12）：3562-3570.（Zhao Jinghua，Zhang Yan，Zhang Wei，et al.The evaluation decision method of the person subjected to execution with heterogeneous information［J］.Control and Decision，2023，38（12）：3562-3570.）