曲轴车削刀具磨损因素交互效应与优化*
王艳平,莫秋云,1b,李 乐,林升垚,王思远
(1.桂林电子科技大学a.机电工程学院;b.广西制造系统与先进制造技术重点实验室,广西 541004;2.桂林福达股份有限公司,广西 541004)
0 引言
曲轴粗车的加工余量相对较大,加之工艺参数的不合理选择,容易导致车刀磨损加剧,刀具磨损过快会引起换刀频繁、加工质量差、生产成本高等问题。因此,减小刀具磨损速度对车削加工至关重要。刀具磨损是多因素耦合过程,切削参数是主要因素之一[1],随着刀具磨损研究的不断深入,因素间的交互作用不应再被忽略,反而应成为研究的重点。
目前,国内外学者针对切削加工中切削参数与刀具磨损的研究主要集中在两方面:其一是切削参数对刀具磨损的影响规律方面。张小粉等[2]通过仿真和实验发现切削速度对切削温度和刀具磨损的影响最大。SELVAKUMAR等[3]分析了微车削钛合金的可加工性与优化,通过方差分析得出切削深度对刀具磨损是最显著因素。孔宪俊等[4]探究切削参数对刀具磨损的影响,发现进给量对刀具磨损的影响程度高于切削速度和切削深度。另一方面切削参数优化对高效率、高质量加工具有十分重要的意义。MIA等[5]基于田口信噪比的优化方法对MQL切削条件下硬车削的表面粗糙度、刀具磨损和材料去除率进行了优化。陶亮等[6-7]将切削温度和切削能耗作为目标,采用响应面和遗传算法相结合的方法开展了工艺参数优化研究。黄贤振等[8]提出了一种考虑不确定性因素的车削参数优化方法,并通过数值算例说明了该方法在车削GH4169参数优化中的可靠性。虽然切削参数对刀具磨损的影响规律及优化方法已经被广泛研究和应用,但对于因素间的交互效应及作用机理研究较少。
本文对曲轴车削工艺进行仿真试验,基于Box-Behnken响应面法和多元非线性回归,分析切削参数(主轴转速、进给量、切削深度)效应对最大刀具磨损量的响应,采用NSAG-Ⅱ算法开展切削用量的多目标优化研究,并进行结果验证,从而有效降低刀具磨损速度。
1 曲轴车削模型构建与仿真
1.1 车削模型与网格划分
本研究以某公司车削加工X曲轴为例。考虑到曲轴主轴颈的对称性及计算量,建立了曲轴主轴颈的1/4模型,简化模型如图1所示。车刀型号为CNMG120412 MR 4235,刀杆型号为T9202R02,车刀和刀杆装配后形成的前角γ为-6°,刃倾角λs为-6°,将建立的刀具模型调整为此角度,从而无需建立刀杆模型。

图1 曲轴主轴轴颈简化模型
将1/4曲轴主轴颈模型与刀具模型按照实际加工位置进行装配。采用四面体网格对模型进行网格整体划分,并对刀尖及主轴实际切削部分进行局部加密处理,最终的网格数量为86 141(主轴颈58 237,车刀27 904)。模型装配和网格划分如图2所示。
1.2 材料参数设置
曲轴材料为48MnV,DEFORM的材料库中没有48MnV的材料模型,需要利用材料的基础参数,采用JMatPro计算材料的力学、物理性能参数,并计算不同应变率下的应力应变曲线,用于定义流动应力应变模型。流动应力方程表达式为:
(1)
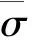
曲轴材料的力学性能参数如表1所示,热物性能和流动应力变化曲线分别如图3和图4所示,刀具的基体材料为WC,其涂层从底层到顶层的材料分别为TiCN/Al2O3/TiN,涂层厚度分别为10 μm、5 μm、2 μm。

表1 48MnV材料力学性能
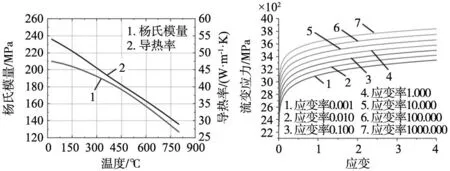
图3 材料热弹性变化曲线
1.3 车削仿真
设定加工的环境温度为20 ℃,与环境的传热系数为0.02 N/s/mm/C,刀具与工件间的传热系数为40 N/s/mm/C,摩擦方式:剪切摩擦,其摩擦系数为0.8。在DEFORM 3D中只能设置主轴转速和进给速度,为了与切削速度和进给量相对应,需要通过合理的转化,二者对应的转化关系为:
(2)
(3)
式中:Vc为切削速度,m/min;D为工件直径,mm;n为主轴转速,r/min;fz为进给量,mm/r;Vf为进给速度,mm/s。
车削加工属于连续加工过程,选用Usui刀具磨损模型较为合适,其中系数a设为1e-06、b为855。计算步数为1000步,每25步保存一次。根据实际加工设置仿真切削参数,主轴转速为300 r/min、进给量为0.4 mm/r、切削深度为1.5 mm。图5a是曲轴车削加工完成后温度场分布,图5b是加工完成后刀具磨损。
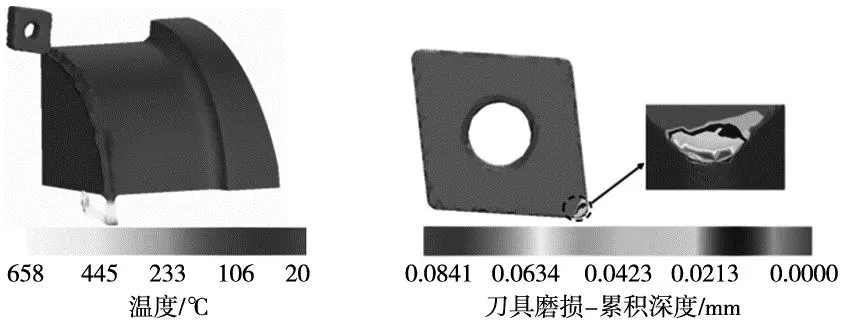
(a) 加工完成后工件温度分布 (b) 加工完成后刀具磨损
由图5a可知,切屑温度明显高于已加工表面温度,这是因为车削产生的大部分热量通过切屑带走。由图5b可知,车刀的前刀面出现磨损,其中刀尖的磨损最为严重,这是因为刀尖的接触压力及接触表面的温度最高,磨损深度随着与刀尖的距离增大而减小。由于刀具的负前角和负刃倾角,后刀面与工件的接触较少,故后刀面磨损较小。
2 因素效应的显著性及交互作用机理
2.1 Box-Behnken试验设计与结果
切削参数对刀具磨损有重要影响,且是能直接调控的变量。以主轴转速、进给速度、切削深度为设计变量,最大刀具磨损量为响应变量。变量水平根据实际机加工过程工艺卡进行选取,并参照式(2)和式(3)进行转换。由于本次试验是数值模拟,在相同的实验数据前提下,不存在试验误差,所以不设计多次中心点试验,试验安排及结果如表2所示。
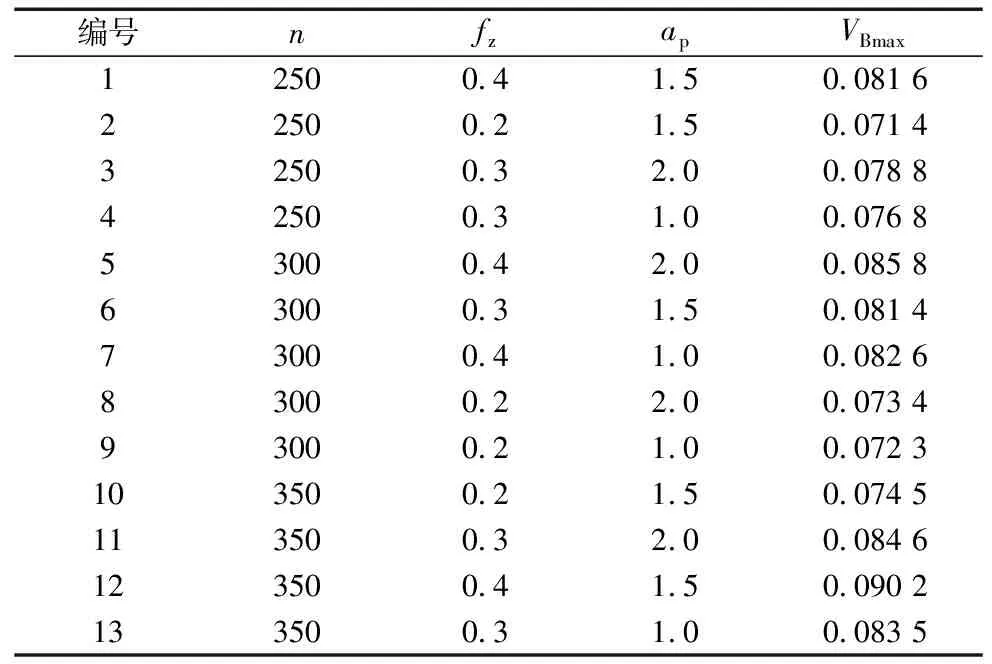
表2 Box-Behnken试验安排及结果
2.2 响应曲面分析及多元非线性回归
在车削加工过程中,切削参数与刀具磨损之间存在非线性关系。因此,建立带有非线性项响应模型并对试验结果进行响应曲面分析,得到因素效应显著性如图6所示。
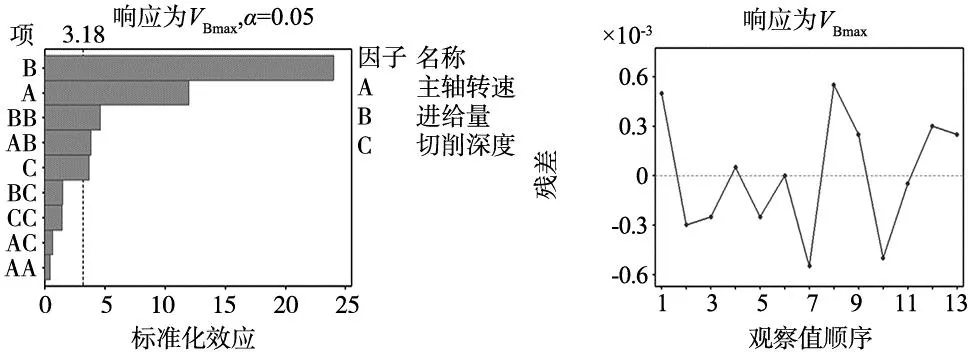
图6 因素效应显著性
从图6可以看出,该模型以P=0.05为显著性水平时,帕累托标准为3.18。在本次试验中进给量和主轴转速是主要显著项,进给量与主轴转速的交互项、进给量的二次项及切削深度是次要显著项,且影响程度依次降低。其他项在本次实验中是非显著项,对刀具磨损的影响程度较小。
依据图6将初步拟合的回归方程中不显著项剔除后,最终得到刀具磨损的回归数学模型如式(4)所示。图7表示与试验顺序对应的刀具磨损残差,最大残差值不超过0.000 6,残差值较小,实验点分布在两侧,无明显规律,表明拟合的效果较好。
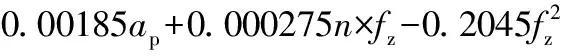
(4)
式中:250≤n≤350,0.2≤fz≤0.4,1≤ap≤2。
2.3 主轴转速、进给量交互效应
图8为主轴转速与进给量对刀具磨损的交互效应,其中切削深度为1.5 mm。
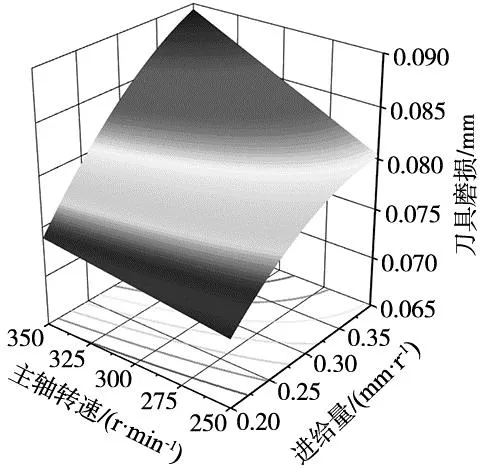
图8 主轴转速与进给量的交互效应
由图8可知,当进给量为0.20 mm/r(低水平)时,刀具磨损量随主轴转速升高的最大增幅为0.003 1;当进给量为0.40 mm/r(高水平)时,刀具磨损量随主轴转速升高的最大增幅为0.008 6,主轴转速对刀具磨损的响应明显依赖于进给量的水平。同时,当主轴转速分别处于低、高水平时,刀具磨损随进给量变大的增幅也有明显差异,进给量对刀具磨损的响应也明显依赖于主轴转速的水平。并且刀具磨损随着进给量和主轴转速的增大而增大,所以进给量与主轴转速之间呈现显著的正向交互作用。
在金属切削过程中,较大的切削力和较高的切削温度通常被认为是导致刀具磨损过快的重要原因[9]。切削温度随着切削速度的增大而升高,切削力变化较小[10]。进给量对切削温度和切削力都有显著影响[11]。
当进给量处于低水平时,随着主轴转速的提高,切削热明显增加,而切削力无明显变化,此时刀具磨损的增量主要是热作用引起的磨损,增量较小;随着进给量的增大,产生更大的切削力和更多的切削热,此时刀具磨损的增量来源于叠加的热力耦合作用引起的磨损,增量较大。当主轴转速处于低水平时,随着进给量的增大,切削力和切削热增加,在热力耦合作用下引起较大的刀具磨损增量;随着主轴转速的提高,产生了更多的切削热,热力耦合作用进一步提升,使得刀具磨损增量也进一步增加。可以依据此交互作用机理,对切削参数进行合理选择。
3 基于NSGA-Ⅱ算法的切削参数多目标优化
3.1 目标函数及约束条件
在进行工艺优化时,不能只追求某一方面的最优,而要结合实际工艺,确定合适的优化目标。粗车是曲轴加工的第一道工序,对表面质量的要求相对较低,但其加工效率会直接影响到后续工序,因此,在优化刀具磨损时加工效率也应作为优化目标。刀具磨损量以拟合的回归方程表征,实际加工多采用单次走刀,所以采用切削单位长度所用时间作为加工效率,如式(5)所示。建立多目标优化函数及约束条件分别如式(6)和式(7)所示。
(5)
Y=Min[(VB,t)(n,fz,ap)]
(6)
(7)
3.2 优化算法及实现
NSGA-Ⅱ算法相比原始遗传算法提出了快速非支配排序算法、拥挤度和拥挤度比较算子及精英策略,其在计算复杂度、优化结果的精度、运算速度和鲁棒性都更有优势[11-12]。采用MATLAB运行算法,设置种群大小N=80、迭代次数经过不断尝试,最终设定为600次,交叉和变异概率分别为0.8、0.05。曲轴车削加工时,获得高加工效率时刀具磨损往往较为严重,二者是相互制约量,在进行多目标优化时,很难同时达到最优,只能获得一系列较优解,使二者达到相对平衡,所以建立了Pareto前沿解,如图9所示。
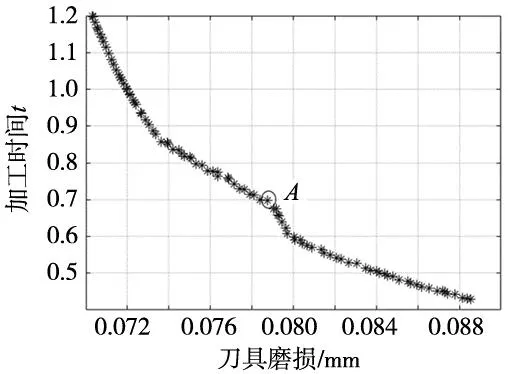
图9 帕累托前沿
由图9可知,随着刀具磨损的增大,加工时间总体呈减小趋势,A点为拐点,A点前后,加工时间都先呈明显下降趋势,然后下降趋势减缓。A点能使加工时间和刀具磨损达到相对平衡状态,A点处的刀具磨损为0.078 7 mm,加工时间为0.699 s,A点的加工参数为;主轴转速336.6 r/min、进给量0.255 mm/r、切削深度1 mm。
3.3 优化参数验证分析
对优化结果取整后,加工参数为:主轴转速336 r/min、进给量0.25 mm/r、切削深度1 mm。将此组加工参数带回搭建的车削仿真模型中,仿真计算结果为0.077 4,与优化结果的误差为1.68%。误差来源可能包括系统误差(回归方程、优化方法)和随机误差(优化结果取整)。
4 结论
(1)主轴转速与进给量对刀具磨损的响应都明显依赖于彼此的水平,切削力和切削热是影响交互效应显著的原因。
(2)基于多元非线性回归和NSGA-Ⅱ算法,对刀具磨损分别进行拟合和优化,获得最优的加工参数n、fz、ap分别为336 r/min、0.25 mm/r、1 mm。优化结果与数值模拟的结果不超过2%,表明该优化方法的可靠性。

