基于Bennett机构的环形可展开桁架设计与分析*
周凯红,尹振巍,黄思敏
(桂林理工大学机械与控制工程学院,桂林 541006)
0 引言
可展机构是一种能够在运输或存储时收缩,而在使用时展开的桁架结构,常用于太空和航空器件。与传统的固定结构相比,可展桁架具有轻量化、可靠性高、可重复使用等优点,因此在航空航天领域有广泛的应用前景。空间可展开天线是一种利用可展结构设计的天线,早期的空间可展天线采用的是不可展开的整体结构,因为当时口径较小。但随着口径需求的增大,现在更多采用可展开的结构设计。根据展开形式的不同,空间可展开天线可以分为固面可展开、环形可展开、充气可展开等多种类型。其中,环形可展开天线以其大口径、高收纳率和轻质量的特点,成为目前应用最广泛的天线类型。
近些年,大型可展桁架已经被广泛应用于空间技术领域。某公司研发的AstroMesh天线,已经应用于多种卫星任务[1-2]。欧洲航空局(ESA)研发出一种双剪叉环形结构和圆锥环形结构的可展桁架,能够满足卫星通信以及对地观测的需要[3]。GUEST等[4]在双剪叉机构基础上进行改进,构建出一种新型环形张拉天线桁架,并通过拉动绳索控制其展开以及收拢,提高了桁架的可靠性和稳定性。我国对空间可展天线研究较早,并在空间可展天线领域取得了多项成果,其中包括四面体式[5-6]、六棱柱式[7-8]、环形桁架式[9]等多种类型的可展天线。SHI等[10]对上下两层展开式环形天线进行改进,提出了不同形式的双环形可展开结构。
大多数可展机构是一种由多个单元构件组合而成的机械结构,在需要时可以紧凑收拢并展开成不同的形状。Bennett机构是一种经典的平面过约束机构,由于结构简单、运动平稳、可靠性高的特性,在机器人、航空航天等领域得到了广泛应用。本文以Bennett机构替代构型为基本单元,通过将多个Bennett机构组合来建立环形可展开天线桁架模型,并对环形桁架性能进行对比评估。
1 环形可展桁架的设计
1.1 Bennett机构
Bennett机构是一种基础的空间多杆过约束机构,其包含4个转动副,通常情况下,机构的4个转动副轴线之间既不相交也不平行[11-12],其基本结构如图1所示。为了确保Bennett机构具有单自由度,需要满足基本条件:两组相对杆的杆长相等,分别为a、b;两组相对转动副的轴线转角相等,分别为α、β;杆长与转动角的大小满足等式bsinα=asinβ;各个转轴沿转动副轴线方向的偏移量为零[13];各个变量θ1、θ2、θ3、θ4随着机构运动状态的变化而变化,但是始终满足下列等式:
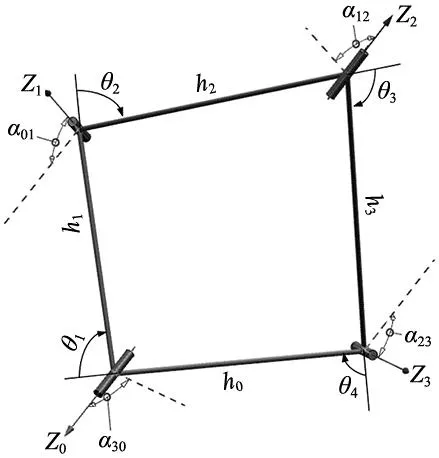
图1 Bennett机构原理图
为了解决这个问题,本文采用了一个名为Bennett替代构型的设计[14-15],如图2所示。该构型在机构的结构和运动规律上与传统的Bennett机构相似,但具有更好的展开性能和折叠性能。替代机构是相对于理论构型来说的,在理论构型中,转动副与连杆均垂直,且完全符合DH法,但是在替代构型中,转动副与连杆发生一定的角度偏移,且替代构型四杆均为等长,其展开四杆可以在同一平面内,展开形状为平面菱形,收拢时四杆可以收拢为一束,实现了完全展开与收拢。

(a)收拢状态 (b)展开过程 (c)展开状态
1.2 Bennett机构的组网方式
为满足大尺度的展开机构需求,可展天线的展开拟合面采用圆柱面,并通过将多个单元组合,构建过渡单元来构成机构网络。在这个机构网络中,单元Bennett机构的过渡单元构造方式如图3所示。
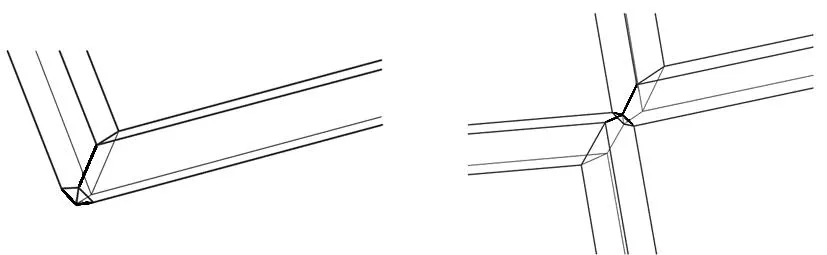
图3 Bennett机构过度单元构造方式
图3中黑色粗线代表转动副。因为替代机构为面对称机构,可以分别在两端Bennett机构连接处使用该方法构造转动副,得到Bennett机构过渡单元,如图4所示。
对于单个可展单元而言,杆的横截面与连接截面之间会形成一定夹角θ,因此,当对多个基本可展单元进行连接时,可以构造出展开状态近似圆柱面的机构,如图5所示。

(a) 单个可展单元 (b) 多个可展单元
以Bennett机构替代构型为基本单元,采用上述过渡单元,在连接时θ保持一定,从而构造出一个如图6所示环状可展桁架。该桁架完全展开为圆柱面,收拢则为长方体,可以大大提高收展比。

(a) 收拢状态(b) 展开过程(c) 展开状态
2 有限元模型的构建
图7展示了4种基本可展单元构型,分别为对角线伸缩单元、剪叉式单元、V型平行杆单元以及Bennett机构替代单元,它们的结构尺寸可以根据需要进行调整,从而得到所需桁架构型。
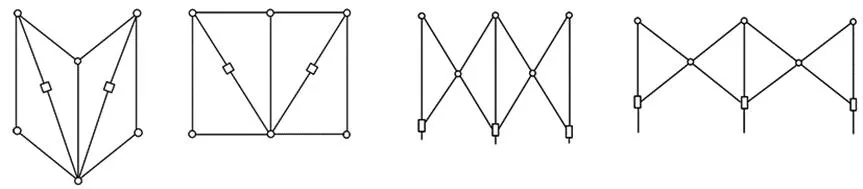
(a) 对角线伸缩单元 (b) 剪叉式单元
为保证环形桁架整体的单自由度,将上述4种基本单元构型按照周向排列,在一定的机构和拉索的作用下,实现同步运动。其中,以对角伸缩式、剪叉式、V型平行杆式3种基本单元构成的环形桁架收拢时向圆心收拢,最终形成一束;而以Bennett替代构型为基本单元构成的环形桁架,在相邻单元之间增加一组折展连杆,以扇形进行收展,最终收拢成一长方体。根据图7中4种基本单元,设计出4种不同环形桁架展开机构,如图8所示。4种环形桁架分别以对角伸缩式、剪叉式、V型平行杆式、Bennett替代构型为基本可展单元,分别记作A、B、C、D四种。

(a)环形桁架A (b)环形桁架B (c)环形桁架C (d)环形桁架D
3 仿真分析
3.1 比刚度分析
本文通过比刚度与比模态频率两个指标来对不同单元构型的刚度、模态和质量进行综合评估,以获得更准确的结果。比刚度为静刚度与质量的比值,静刚度为力与变形量的比值。比刚度可以反映出材料的质量、力和变形量之间的关系,比刚度数值越大,说明同刚度下质量更小,或者同质量下刚度更大。比模态频率为模态频率与质量的比值。本文在分析模态频率时只对比分析前三阶,比模态频率的数值越大越好,数值越大则更不容易发生共振。
本文使用ANSYS Workbench软件,分别建立4种不同环形桁架可展开结构有限元模型,环形桁架展开口径为10 m,整体杆件使用碳纤维材料,材料参数如表1所示。

表1 环形桁架材料参数
通过使用静力学模块和模态分析模块进行耦合仿真,固定桁架一端,并在另一端施加10 N正压力,即可得到各个环形桁架的变形量。表2展示了由4种基本单元构成的环形桁架的静刚度和比刚度的仿真结果。这些结果可以用于评估环形桁架的刚度和稳定性,以及为优化设计和改进提供指导。
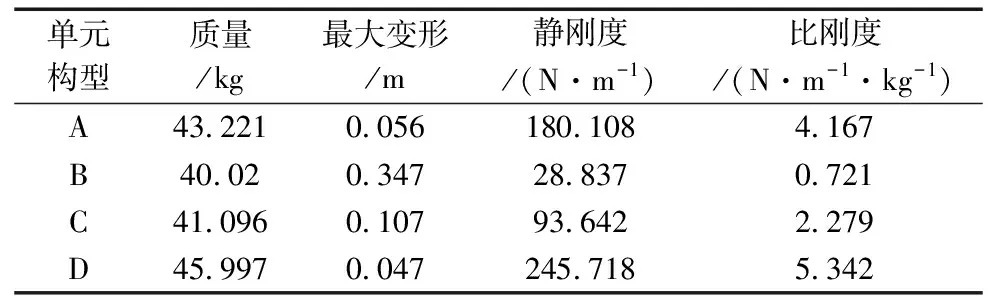
表2 环形桁架比刚度分析
根据仿真结果可以看出,环形桁架B比刚度过低,环形桁架A与D相对比刚度较高,分别为环形桁架C的1.83倍与2.34倍,因此环形桁架D具有较高的刚度。
3.2 比模态频率分析
通过使用ANSYS软件仿真分析,分别得到环形桁架A、B、C、D的前三阶振型图,如图9~图12所示。
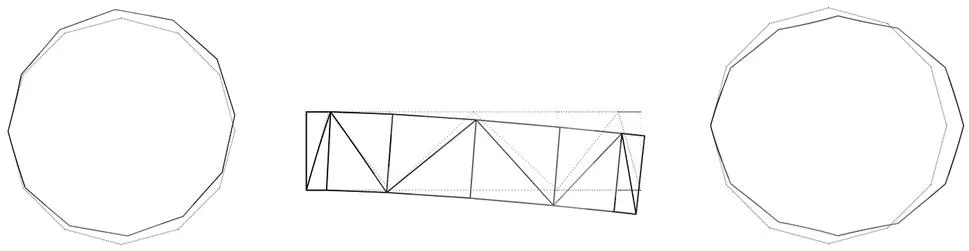
(a)一阶振型图(面内弯曲) (b)二阶振型图(面外弯曲) (c)三阶振型图(面内对称收缩)

(a)一阶振型图(面内弯曲) (b)二阶振型图(面外弯曲) (c)三阶振型图 (面外扭转)
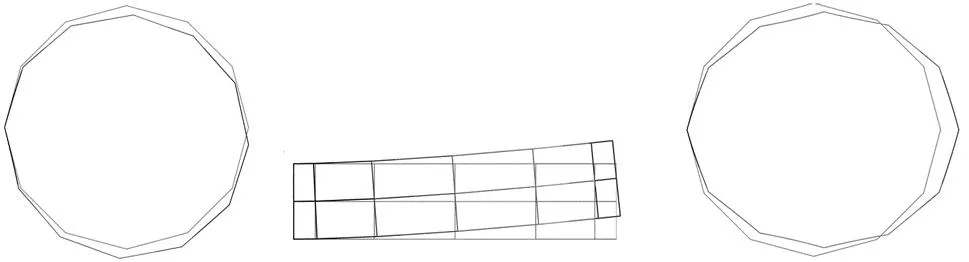
(a) 一阶振型图(面内弯曲) (b)二阶振型图(面外弯曲) (c)三阶振型图(面内对称收缩)
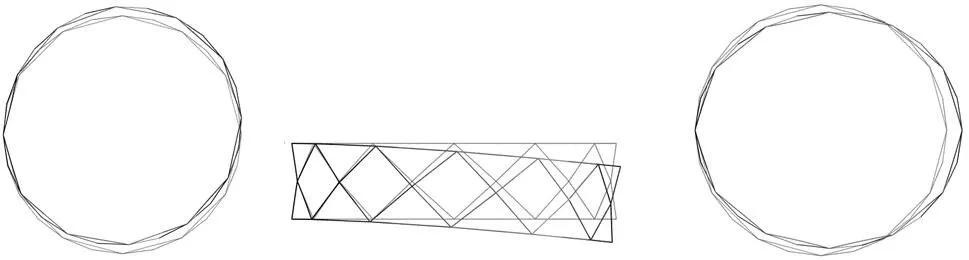
(a) 一阶振型图(面内弯曲) (b)二阶振型图(面外弯曲) (c)三阶振型图(面内对称收缩)
根据仿真结果可以看出,B环形桁架的第三阶振型为面外扭转,其他3种构型第三阶振型均为面内对称收缩,并且A、C、D三种不同环形桁架前三阶振型都分别相同,对其仿真结果分析如表3所示。
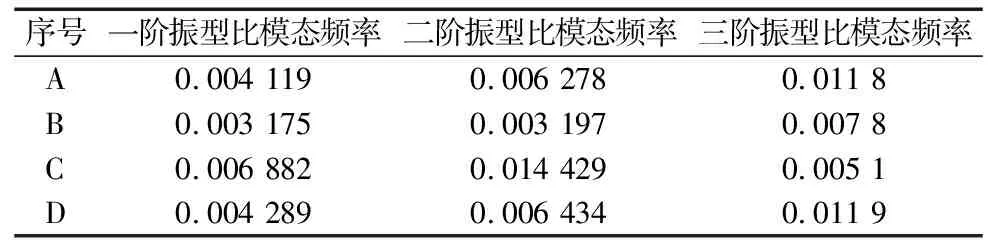
表3 环形桁架比模态频率分析 (Hz·kg-1)
根据表3仿真结果,环形桁架B的前三阶比模态频率均为最低,环形桁架C的前两阶比模态频率高于A和D,但第三阶比模态频率却明显小于另外两个桁架。环形桁架D比模态频率均高于环形桁架A,第一阶比模态频率约高4.1%,第二阶比模态频率约高2.4%,第三阶比模态频率则几乎相同,综合来看,环形桁架D具有良好的稳定性。
4 结束语
本文提出了一种基于Bennett机构的环形可展桁架。该桁架使用Bennett机构替代构型作为基本单元构型,采用过渡单元法构建出环形可展桁架。通过使用ANSYS仿真软件与其他3种环形桁架进行分析对比,仿真结果表明,使用Bennett机构作为基本单元构型可以提高桁架的刚度和稳定性。这是因为Bennett机构具有很好的平面稳定性,能够有效地抵抗外部荷载的作用。另外,通过过渡单元法构建的环形可展桁架也能够实现较高的展开比,进一步提高了其适用范围和灵活性。

