往复摆动加载测试过程中的运动学分析*

姚良博,李金峰,吴艺波,弓 宇,程 曼

(1.中机生产力促进中心有限公司,北京 100040;2.国家市场监管重点实验室(智能机器人安全),佛山 528300;3.广东产品质量监督检验研究院,佛山 528300)

0 引言

往复摆动运动是机械传动领域比较常见的一种运动形式,广泛应用于航空、汽车、船舶以及工业机器人等设备。特定的运动形式决定了轴承、减速器等传动系中关键零部件的应用工况,如:十字万向节中的节叉轴承、飞机机体的滚动轴承、工业机器人中的减速器及轴承等[1-5]。在这些关键零部件的润滑特性、运动特性、精度及可靠性等性能的试验验证中,需要提供符合实际应用工况的循环加载形式,即往复摆动加载运动。考虑到测试成本等因素,通常利用连续回转加载运动施加恒定负载扭矩以及恒定转速来进行试验[6]。然而,由于在往复摆动加载运动过程中存在频繁的加、减速运动阶段,被测试对象所承受的负载也时刻于动态变化中,这必然会导致同恒转速、恒扭矩条件下的测试结果形成一定的差异。虽然恒扭矩加载试验在前期得到了一定的应用[7],但是当前业界更加倾向于开展符合实际运动工况的测试,如工业机器人及其关键零部件的相关测试,尤其是疲劳和可靠性测试倾向采用往复摆动加载试验[8-9]。然而,根据广泛调研,当前行业内对往复摆动加载测试过程中的运动学过程未达成统一认识,甚至一些机构有着错误的认知,这会直接导致无法获得摆动加载测试过程的最优控制,取得最高的测试效率,甚至导致测试结果的不准确,从而承担巨大的时间成本和经济成本。综上所述,为了保证测试过程中有效施加负载的合理性及准确性,有必要从理论上对往复摆动加载测试过程中加载单元的运动学特性进行系统的分析。

本文以工业机器人用RV-40E减速器的摆动疲劳加速试验为研究对象,利用Lagrange动力学方法对单侧配重和对称配重两种加载单元的运动学特性进行理论分析,推导出往复摆动过程中的有效加载扭矩计算公式。再利用Adams软件对该往复摆动过程进行运动学仿真,分析其在指定摆动运动规律下有效加载扭矩的变化过程。最后,通过选用市面知名品牌的机器人减速器开展往复摆动试验。同时,分析不同形式加载单元对摆动疲劳加速试验的影响,为往复摆动疲劳寿命试验的设计提供一定的指导。

1 运动学过程分析

Lagrange动力学方法是一种基于系统能量(动能和势能)和广义坐标系的动力学分析方法,利用该方法建立动力学方程不需要依赖空间坐标系,也不需要分析系统内部的约束力,从而可以在很大程度上简化系统动力学方程的推导过程[10]。即使针对小角度的位移运动,也可以推导得出形式简单的动力学方程,是分析关节机器人运动学过程的常用分析方法[11-12]。

L=EK-Ep

(1)

式中:EK表示系统动能,Ep表示系统势能。

由此可知,对于任何机械系统,Lagrange函数L可表示为其总动能与总势能的差值。

对处于任意广义坐标系qi(i=1,2,…,n)下的机械系统,其动力学方程为:

即:

(2)

式中:fi为广义力,根据qi的不同可以表示力(直线坐标)或力矩(角度坐标)。

1.1 单侧配重

图1a为单侧配重摆臂结构,摆臂重心到旋转中心O的距离为r,摆臂在A、B两点间做往复循环的摆动运动,单侧摆角为θ,摆动范围为θ1;图1b为摆臂的受力分析简图,摆动角加速度为α,角速度为ω,设定摆臂及配重的总质量为m,摆臂处于竖直位置时的重心位置C为势能0点。则有摆臂在运动过程中的能量方程,动能方程为:

(3)

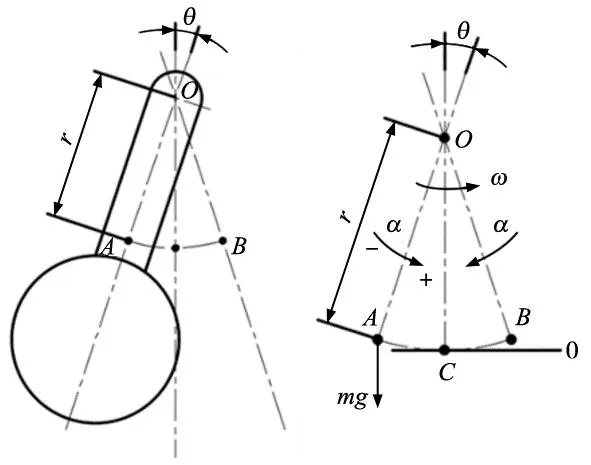
(a) 单侧配重摆臂结构示意图 (b) 受力分析简图

势能方程为:

Ep=mgr(1-cosθ)

(4)

根据Lagrange动力学方法,作用在旋转中心O的力矩为:

即:

T=J·α+mgrsinθ

(5)

式中:J为摆臂的惯量,α为角加速度矢量。

由式(5)可以看出,单侧配重的加载力矩由加速度引起的惯性矩和重力引起的重力矩两部分组成。其中,重力在运动过程中的做功与相对旋转角度即摆臂所处位置有关,与加速度和速度方向均无关;加速度引起的惯量矩与摆臂的加速度方向有关且方向相反。因此,在单侧配重形式下的摆动加载运动中,惯性矩和重力矩的做功正负没有固定的逻辑联系,两者之间的关系由摆动运动自身的运动规律决定。

1.2 对称式配重

对称式配重是指配重关于旋转中心中心对称,可以分为两种形式:①对称式摆臂;②圆盘或惯量盘。由于2种形式的配重在往复摆动过程中的动力学特性一致,因此这里仅以对称式摆臂配重为例,进行动力学分析。

图2a为对称式配重摆臂结构,摆臂重心处于旋转中心O点,摆臂在A、B两点间做往复循环的摆动运动,单侧摆角为θ,摆动范围为θ1;图2b为摆臂的受力分析简图,摆动角加速度为α,角速度为ω,设定摆臂的总质量为m,摆臂所处重心位置O为势能0点,由于摆动过程中重心位置不变,因此势能始终为0。则有摆臂在运动过程中的能量方程,动能方程为:

(6)

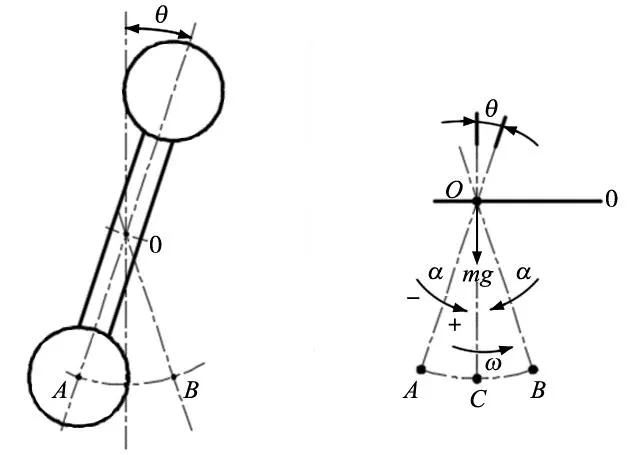
(a) 对称式配重摆臂结构示意图 (b) 受力分析简图

势能方式为:

Ep=0

根据Lagrange动力学方法,作用在旋转中心O的力矩为:

即:

T=J·α

(7)

式中:J为摆臂的惯量,α为角加速度矢量。

由式(7)可以看出,对称式配重的加载力矩仅由加速度引起的惯性矩提供。在整个的摆动运动中,重力在运动过程中不做功,只有加速度引起的惯量矩做功,且惯量矩方向同加速度方向始终相反。

2 实例分析

为验证以上动力学分析过程及结果,本文选取工业机器人用减速器RV-40E-121为研究分析对象,分别选取单侧配重和对称式摆臂配重各一组参数进行理论计算、Adams仿真,并选取RV-40E-121型号减速器进行试验验证。试验采用加速寿命试验,选取载荷为加速系数,且最大载荷不超过减速器额定载荷的2.5倍。减速器参数、配重参数及运动参数如表1、表2所示。

表1 减速器参数表

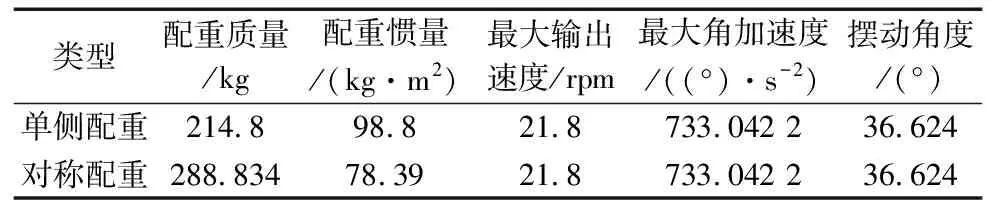
表2 配重及运动参数表

当前,工业机器人实际应用工况的加减速运动控制算法常用的如基于S型曲线的算法、基于泰勒展开的算法、基于NURBS曲线的算法、基于B样条曲线以及基于正弦函数的算法等[13-17]。本文的研究对象为工业机器人中的单关结,考虑到单次循环内的冲击等因素,这里选用基于正弦函数的控制算法,并且单侧配重和对称式配重选用相同的运动规律参数。单周期内其角度、角速度及角加速度的规律曲线如图3所示。

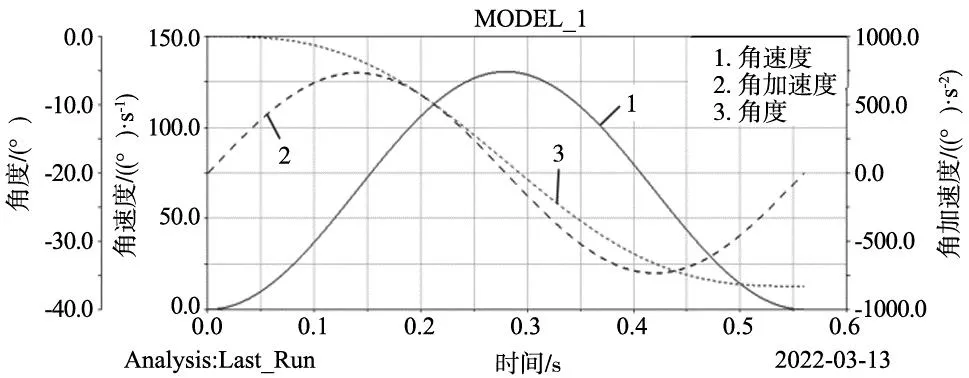
图3 单侧配重和对称式配重运动规律

两种配重形式下的摆动区间位置选择如图1和图2所示,均关于竖直方向对称,且往复摆动运动的起始位置均选为摆动区间的左端,即两图中的A点。

2.1 理论计算

2.1.1 单侧配重工况

单侧配重工况的运动轨迹与受力分析图如图1所示,图3显示了摆臂由A点经C点到B点的运动规律,摆臂由B点返回至A点同样按照该规律运行。如图1所示,选定由A点到B点方向为正方向,根据图3中的运动规律分析可知,从A点到C点的运动过程,加速度方向同重力作用方向一致,则有惯量矩与重力矩方向相反;从C点到B点的运动过程,加速度方向同重力作用的方向也是一致的,所以其惯量矩与重力矩方向亦相反。因此,单侧配重形式下单周期内惯性矩和重力矩方向始终相反。

根据式(5)计算可得,单周期内惯量矩和重力矩始终保持方向相反,其单周期内变化曲线及加载力矩变化曲线如图4所示,周期内的加载扭矩变化呈类正弦规律,起始点扭矩由重力矩提供,其值为415.72 N·m,最大加载扭矩为931.45 N·m。

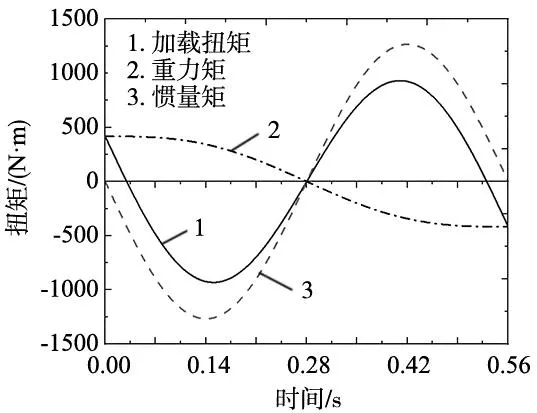
图4 单侧配重单周期内加载力矩变化曲线示意图

2.1.2 对称式配重工况

对称式配重工况的运动轨迹与受力分析图如图2所示,图3显示了摆臂由A点经C点到B点的运动规律,摆臂由B点返回至A点同样按照该规律运行。如图2所示,选定由A点到B点方向为正方向,由于整个摆动运动过程中重力不参与做功,则根据式(7)计算可得摆臂由A点经C点到B点的加载力矩,周期内的加载扭矩变化呈类正弦规律,最大加载扭矩值为1 002.75 N·m,其单周期内的变化曲线如图5所示。

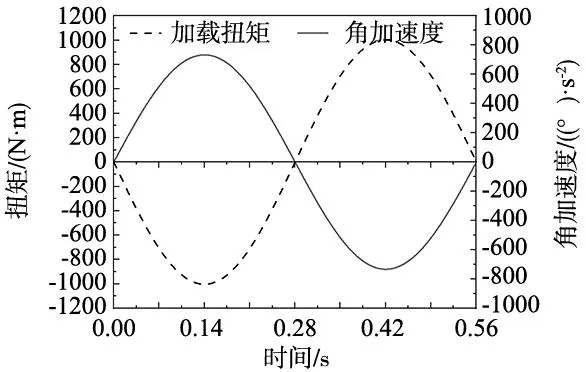
图5 对称式配重单周期内加载力矩变化曲线示意图

2.2 Adams仿真分析

Adams是一款功能强大的机械系统动力学性能仿真平台,在研究机械系统动力学过程中运动部件的力和载荷方面应用广泛[18-19]。

如图6所示,分别为单侧配重和对称式配重的简化模型,将旋转关节施加到配重摆臂的旋转中心代替机器人减速器,可通过测量摆动过程中的关节受力得到机器人减速器摆动运动过程中的负载扭矩。此外,在旋转关节处施加运动规律MOTION:12.794*SIN(2*PI*time/0.56),函数为摆臂的角加速度函数,其周期内的变化曲线如图3所示。

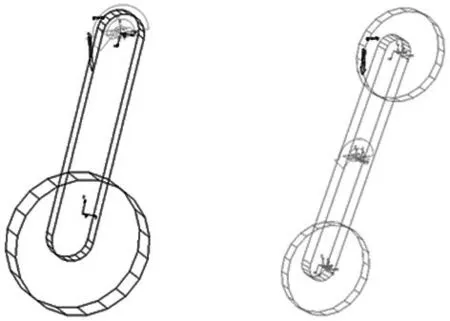
(a) 单侧配重 (b) 对称配重

两种工况下的Adams仿真结果如图7、图8所示,分别同图4和图5对比可以看出,根据理论计算得到的单周期内加载力矩变化规律同Adams仿真分析得到的结果一致。从表3的统计数据可知,理论计算所得的两种工况下单周期内最大加载力矩值与Adams仿真所得的结果偏差分别为-0.17%和-0.07%。因此,上述的分析结果可以表明:理论推导的摆动过程的加载力矩计算式(5)和式(7)是正确的。

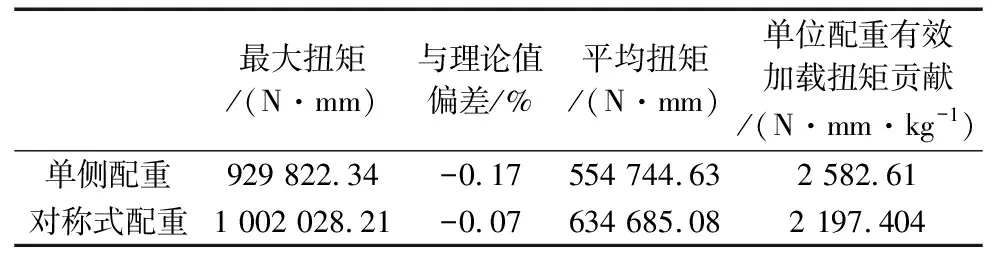
表3 仿真结果数据统计表

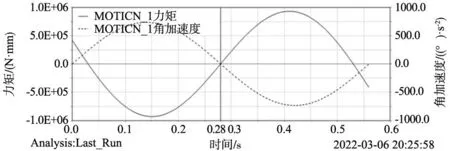
图7 单侧配重单周期内加载力矩仿真结果

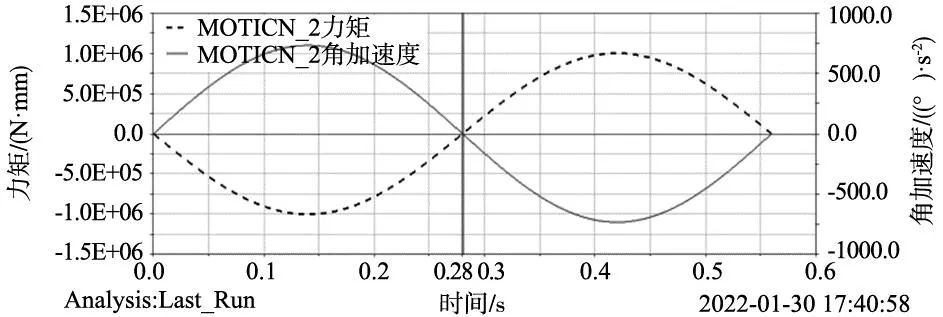
图8 对称式配重单周期内加载力矩仿真结果

根据工业机器人减速器等效寿命计算公式[20],周期内的平均加载扭矩和平均转速为影响等效寿命计算结果的两项关键参数。本文的两种工况选取的运动规律一致,因此周期内的平均转速相等。从表3可知,两种工况下单位配重在相同的运动规律下最终可提供的有效加载扭矩分别为2 582.61 N·mm/kg和2 197.404 N·mm/kg。由于配重越大,摆臂运动过程中对减速器产生的倾覆力矩越大,对减速器寿命的影响也会越大。此外,单侧配重的加载工况更加符合工业机器人减速器的实际应用工况。因此,对于本文所述的摆动加载应用测试特点,选取单侧配重的加载形式更加科学。

2.3 试验验证

对于对称摆臂配重而言,摆臂重心在运动过程中始终与旋转中心重合。由式(7)可以看出,重力在运动过程中可以认为不做功,只有加速度引起的惯量矩做功,所以其运动学过程相对而言比较容易理解。因此,本文的试验验证工作仅针对单侧配重摆臂工况开展。

试验验证在自主研发的机器人用减速器摆动疲劳寿命试验台上开展,主要包括伺服电机及驱动器、HBM扭矩传感器、RV40E-121减速器、减速器安装支座、试验测试摆臂配重、安装底座、轴承座等组成,设备并配有温度传感器、振动传感器等实时监测测试过程,设备简要结构及实物图如图9所示。试验过程中,通过伺服驱动器控制伺服电机,按照指定的运动规律进行往复摆动,并通过PLC实时采集对应时刻下扭矩传感器的扭矩值,同时记录伺服电机编码器的旋转角度,同步采样频率为50 Hz。其中,试验过程中伺服电机的运动规律以及摆臂的配重参数均参见表2和图3。

(a) 结构简图 (b) 设备实物图

采集的旋转角度值通过式(8)所示的求导公式可得到摆动运行过程中的角加速度,进而通过式(5)得到试验过程中的实时加载扭矩,实时加载扭矩和扭矩传感器的实际测量扭矩对比图如图10所示。

(8)

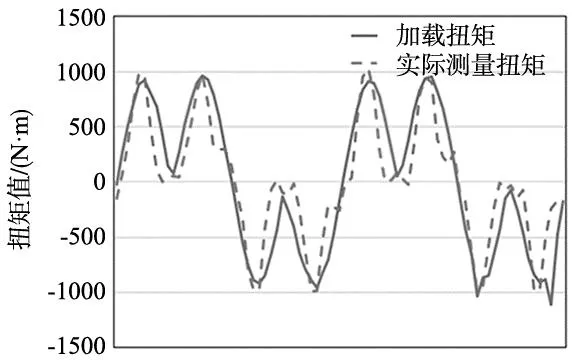
图10 试验过程中实时加载扭矩和实际测量扭矩变化示例图

从图10中可以看出,对比完全通过理论计算所得的加载扭矩曲线,如图4所示,仍存在一定的差异,分析是由于伺服电机角度编码器的分辨率以及整体的采样频率限制所引起的数据失真引起的。但是,从试验采集数据出发利用推导的理论公式计算的结果是跟扭矩传感器实时采集的结果对比来看,两组数据的变化趋势和峰-峰值区间基本一致。因此可以表明:理论推导的单侧配重工况下摆动过程的加载力矩计算式(5)同实际的测试结果相吻合。

3 结论

研究分析结果表明,在单侧配重形式下的摆动加载运动中,惯性矩和重力矩的做功正负没有固定的逻辑联系,两者之间的关系由摆动运动自身的运动规律决定。对称式配重的加载力矩仅由加速度引起的惯性矩提供,在整个的摆动运动中,重力在运动过程中不做功,只有加速度引起的惯量矩做功。此外,水平方向的摆动运动同竖直方向对称式配重的运动学特性一致,在往复摆动运动过程中重力均不参与做功。

此外,单侧配重在单位重量下可以产生更高的有效加载扭矩,提供相同的加载扭矩产生更小的倾覆载荷力。同时也表明在摆动疲劳可靠性试验中,应用单侧配重加载单元更加科学合理。