差动驱动并联机器人设计与运动学分析*

任 彪,韩哈斯敖其尔,2,黄胡泽,李耀彬,2,吴清文,2

(1.中国科学院长春光学精密机械与物理研究所空间机器人工程中心,长春 130033;2.中国科学院大学材料科学与光电技术学院,北京 100049)

0 引言

并联机器人以其结构紧凑,刚度高,运动精度高等特点常常被用作微操作机器人机构,其在三维空间的微小移动精度可以达到亚微米甚至是纳米量级。GOUGH[1]开发出一套六自由度并联机构用于轮胎检测之后,并联机器人机构由于其独特的优势,在航空航天[2]、运动模拟系统[3]、精细手术医疗器械[4]、精密调姿机构[5]、数控加工机床[6]等众多方面得到了越来越广泛的应用。

目前,高精度六自由度并联微动机构实现微位姿调整的方案多采用两种传动方式,第一种是利用伺服电机驱动精密行星滚柱丝杠来实现较高精度的传动和定位[7],一般精度可以达到微米级别,但是成本较高。第二种是利用压电陶瓷驱动柔性铰链机构来实现高精度定位和传动[8],一般精度可以达到亚微米级别,但是成本更高。

本文依托于某望远镜预研项目,基于偏置柔性虎克铰链和Stewart并联机器人的结构,利用双螺旋副差动传动的方案设计了一款6-RR-RP-RR构型的6-DOF并联机器人,既有效提高了机构的传动精度而且降低了精密定位平台的成本,并在设计中采用柔性虎克铰链代替传统的刚性虎克铰链,消除铰链间隙,保证了微动平台精度。

1 差动式并联机器人结构设计

1.1 位移驱动腿结构设计

单足位移驱动器的性能好坏直接决定了整个并联机器人的性能和精度,为此对其提出了两种设计方案。

1.1.1 串联式差动位移驱动腿

在该方案中,支腿内部结构如图1所示。

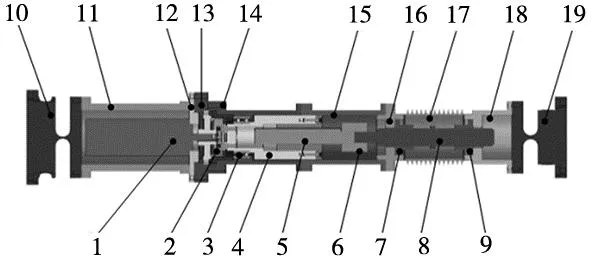
1.伺服电机 2.谐波减速器 3.双联角接触球轴承 4.中间驱动件 5.滚珠花键 6.联轴器 7.螺母件1 8.丝杠 9.螺母件2 10.下铰链 11.轴承套筒 12.电机法兰 13.减速器法兰 14.减速器套筒 15.套筒 16.螺母件法兰 17.波纹管 18.上套筒 19.上柔性铰链

伺服电机经谐波减速器的减速作用后,将转矩传递给滚珠花键副,滚珠花键轴和丝杠轴通过联轴器相连接,在丝杠两端分别有螺距为1.2 mm和1.0 mm的螺纹,通过丝杠两端螺纹螺距的不同而形成差动传动,以此方法来提高支腿的传动和定位精度。该方案设计的支腿中的双螺旋副采用串联形式布置在一根丝杠的两端,所以将这种支腿称作串联式差动位移驱动腿。用该方案设计支腿,在单支腿的运动行程的设计指标为±3 mm时,单支腿的长度高达610 mm,而支腿高度太高将影响整机平台的刚度,由此提出了支腿设计的第二种方案。

1.1.2 并联式差动位移驱动腿

在该方案中,支腿内部结构如图2所示。

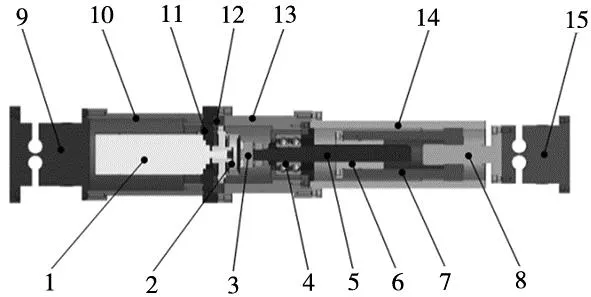
1.伺服电机 2.谐波减速器 3.连接件 4.双联角接触球轴承 5.滚珠花键轴 6.滚珠花键母 7.中间驱动件 8.丝杠 9.下柔性铰链 10.电机套筒 11.电机法兰 12.减速器法兰 13.中间套筒 14.上套筒 15.上柔性铰链

伺服电机经谐波减速器的减速作用后,将转矩传递给滚珠花键副,滚珠花键母和驱动件通过螺钉连接而相对固定,在驱动件的内表面和外表面分别有螺距为1.2 mm的内螺纹和螺距为1.0 mm的外螺纹,驱动件上的外螺纹和在外面固定的套筒的内螺纹相互配合,驱动件上的内螺纹和丝杠上的螺纹相互配合,通过内外螺纹螺距之间的不同而形成差动传动,以此方法来保证支腿的传动和定位精度同时降低支腿的高度。该方案设计的支腿中的螺旋副采用并联形式布置在一个零件的内外表面,所以将这种支腿称作并联式的差动位移驱动腿。采用该方案时,在单条支腿的运动行程的设计指标同样为±3 mm时,单支腿的高度为524.5 mm,比串联式差动传动方案的支腿高度少85.5 mm,因此该方案有利于提升整机平台的刚度。

1.2 柔性铰链设计

按照该并联平台自由度要求,将上下铰链均设计为RR偏置柔性虎克铰链,其结构示意如图3和图4所示,该铰链较之于无偏置量的虎克铰链具有更大的工作空间和更高的刚度[9]。对比常见的几种柔性铰链缺口类型,从其运动范围和刚度来看,圆弧缺口型柔性铰链运动精度最高且刚度最好,但其运动范围较小[10],所以圆弧型柔性转动副更适合于高精度定位装置的设计与制造[11]。综合考虑柔性材料的各种参数,本文的设计中柔性铰链的材料选择为钛合金TC4。

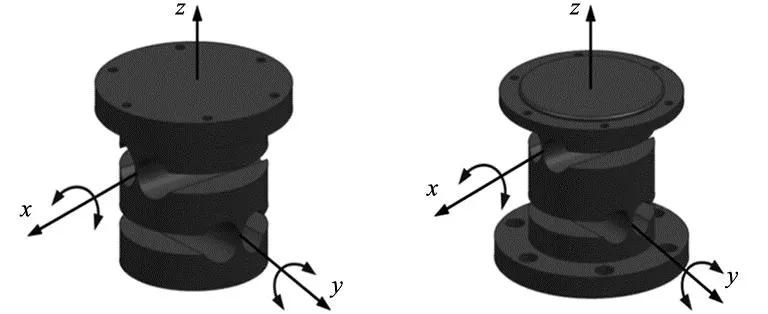
图3 RR偏置柔性虎克铰链(上铰链)

1.3 微动平台整机结构设计

接着对两种驱动腿方案组成的平台整机分别进行结构设计,串联式差动六自由度并联机器人整机结构如图5所示,并联式差动六自由度并联机器人整机结构如图6所示。

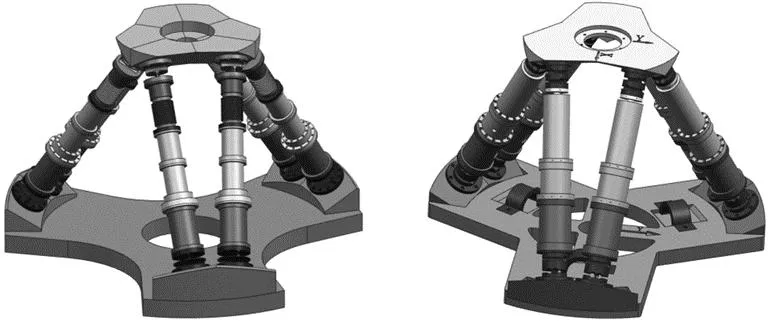
图5 串联式差动六自由度并联机器人

对比以上两种差动方案设计而成的并联机器人整机结构,由于并联式差动位移驱动腿设计而成的整机在相同结构设计参数下具有更小的包络尺寸,因此有利于整机平台的整体刚度,所以确定最终的设计为由并联式差动位移驱动方案设计而成的六自由度并联机器人。后续运动学的分析和仿真等工作同样都是基于并联式差动传动设计而成的六自由度并联机器人。

2 柔性铰链柔度建模与分析

柔度是柔性铰链最重要的性能参数,本部分根据柔度坐标变换方法,建立了偏置柔性虎克铰链的总体柔度模型,并对铰链结构参数对其性能的影响进行了理论分析。

2.1 柔性铰链柔度建模

图7为直圆缺口型单轴柔性铰链示意图,对于该铰链的柔度推导,采用的方法是将其一端施加固定约束使其成为固定端,另一端作为自由端并在其表面中心作用六维力,将柔性铰链整体看作变截面的悬臂梁。基于弹性小变形的假设,在材料力学与弹性力学的基础上,将圆心角作为积分变量推导出铰链各柔度表达式。对其进行坐标变换可以得到六维力作用下,该柔性铰链对应的柔度矩阵具有式(1)所示结构,各元素表达式详见文献[12-13]。

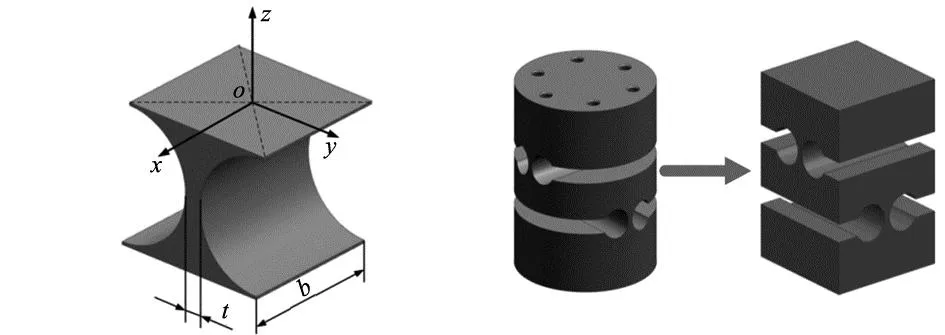
图7 单轴直圆型柔性铰链模型

(1)

为方便求解RR偏置柔性虎克铰链的柔度矩阵,首先对其做一步近似,将我们所研究的圆形轮廓的铰链近似为方形轮廓,如图8所示。因为这种近似对铰链变形区域的改变极小,所以该近似所产生的柔度误差可以忽略。近似后铰链具有如图9所示的构型,其柔度特性可以通过其自由端相对于固定端的变形来描述,载荷向量和位移向量应用于自由端表面中心。将铰链自由端中心处的变形矢量与同点的载荷矢量连接,根据线性弹性材料和小位移的假设,公式为:

图9 RR偏置柔性虎克铰链模型

u=Cf

(2)

式中:u为位移矢量,u=[uxuyuzθxθyθz]T;f为载荷矢量,f=[FxFyFzMxMyMz]T;C为6×6的柔度矩阵。

如图9所示,如果将六维负载f={FxFyFzMxMyMz}施加于偏置柔性虎克铰链的自由端表面,则该铰链产生的变形可以通过坐标变换法求得。通过坐标的平移和旋转,六维力矢量f可以转化到单个直圆缺口型铰链A和B的上端面Ⅰ和Ⅱ。然后,进一步通过坐标变换移回偏置柔性虎克铰链上端表面,可以计算单轴铰链的变形D1和D2,将两个单轴铰链的变形相加后,可以得到偏置柔性虎克铰的总体变形[14]。

(3)

由此可得柔度转换公式可以表达为:

C=T·C0·TT

(4)

式中:坐标变换矩阵为:

(5)

式中:

式中:Dx、Dy和Dz分别为坐标系沿x轴、y轴和z轴的位移,α、β和γ分别为坐标系围绕x轴、y轴和z轴的旋转角度。

对于该偏置柔性虎克铰链,载荷施加在铰链的上端表面。Ⅰ表面上的负载通过平移变换S1和旋转变换R1转移到上端表面,弯曲铰链A位移矩阵S1以及旋转矩阵R1如式(6)所示。

(6)

同样的,Ⅱ表面上的负载通过平移变换S2和旋转变换R2平移到右端表面。弯曲铰链B的位移矩阵S2以及旋转矩阵R2如式(7)所示。

(7)

由柔度的串联公式可知,将两个单轴铰链的柔度相加即可得到偏置虎克铰链的总柔度。故偏置柔性虎克铰链柔度矩阵C中各元素表达式如式(8)～式(17)所示。

(C51+C15)·(l1+l2+2R)-(C24+C42)·l2

(8)

(C51+C15)·l2-(C42+C24)·(l1+l2+2R)

(9)

Cuz-Fz=2C33

(10)

Cθx-Mx=C44+C55

(11)

Cθy-My=C44+C55

(12)

Cθz-Mz=2C66

(13)

Cθy-Fx=C44·l2+C55·(l1+l2+2R)-C42+C51

(14)

Cθx-Fy=-C44·(l1+l2+2R)-C55·l2+C42-C51

(15)

Cuy-Mx=-C44·(l1+l2+2R)-C55·l2+C24-C15

(16)

Cux-My=C44·l2+C55·(l1+l2+2R)-C42+C51

(17)

采用有限元法对上述柔度计算式进行验证,表1给出了上铰链的结构参数,建立上铰链对应的有限元模型,在铰链末端分别施加单位载荷Fx=Fy=Fz=1 N、Mx=My=Mz=1 N·m,其自由端的变形即为柔度[15],记录铰链转动柔度结果列于表2。

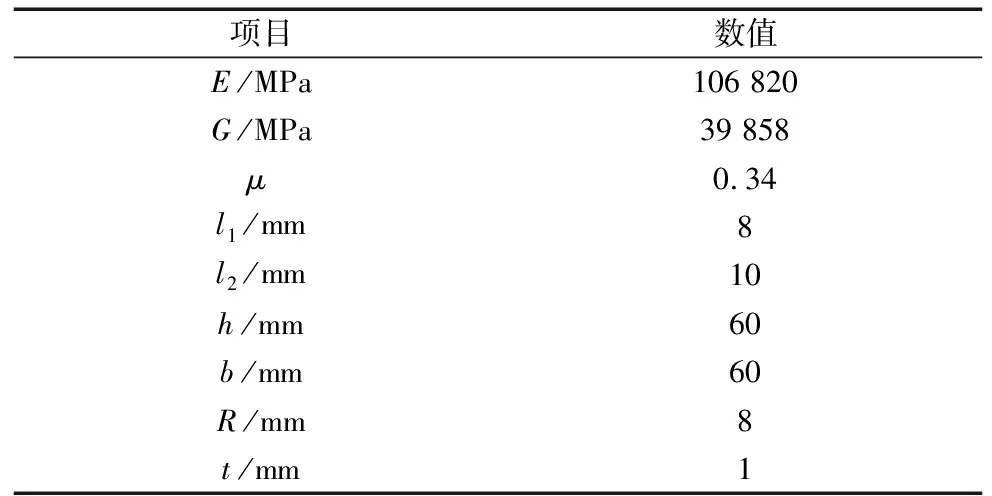
表1 上铰链参数

表2 转动柔度仿真结果

由表1和表2可知,上铰链转动运动方向上的柔度理论值和有限元值的相对误差保持在3.6%以内,从而证明了该铰链柔度表达式的正确性。

2.2 偏置柔性虎克铰链柔度模型分析

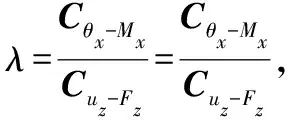
根据式(10)～式(12)中各柔度系数的表达式,可以得到铰链在功能方向和非功能方向上的柔度随各结构参数的变化规律。在此将铰链参数R和t分别作为变量来研究其对铰链性能的影响,而将铰链其他参数按照表1的值给定。

将R作为变量,取值范围为2～10 mm,由图10分析结果可知,随着直圆型缺口半径R的增加,转动柔度和拉伸柔度都呈上升趋势。

图10 铰链缺口半径R对铰链性能的影响

将t作为变量,取值范围为0.1～1.5 mm,由图11分析结果可知,随着铰链最小壁厚t的增加,转动柔度和拉伸柔度都呈下降趋势。

将R和t同时作为变量来分析其对柔度比的影响,图12结果表明随着R和t越小,柔度比值越大,则铰链性能越好。且铰链最小壁厚t对其柔度比的影响比铰链缺口半径R对柔度比的影响更加显著。

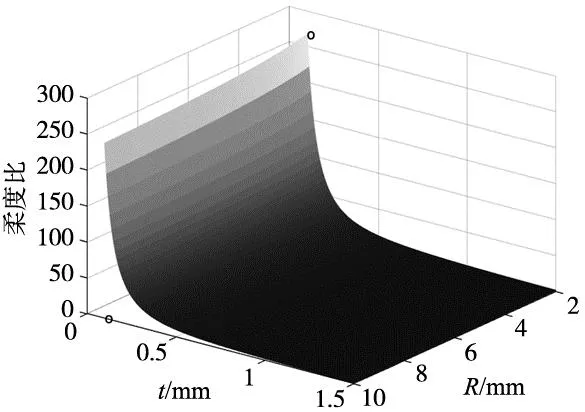
图12 R和t对铰链性能的联合影响

2.3 铰链力学仿真验证

对于RR铰链结构参数具体数值的确定需要对铰链进行力学仿真,使其在最小值时铰链所受的应力小于钛合金TC4的疲劳强度,以满足铰链的强度要求。

根据平台结构尺寸和铰链各结构参数对其性能的影响分析,取铰链最小壁厚t=1 mm,铰链缺口半径R=8 mm。根据平台承载能力设计要求和平台自重对下铰链施加延空间直角坐标系各轴40 N的力,得到铰链仿真结果应力云图如图13所示,铰链最大综合应力为188.83 MPa。证明上下柔性铰链的最大综合应力都小于所用材料的许用应力,因此满足要求。

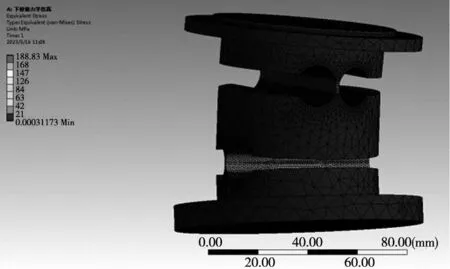
图13 下铰链力学仿真结果

3 并联机器人运动学建模

3.1 并联机器人整机构型参数

位移驱动器包含移动副与转动副相耦合的差动螺旋副的结构形式,由此可知该六自由度并联平台位移驱动腿的驱动链为RR-RP-RR支链,图14为其运动链的示意图。

图14 支腿运动链示意图

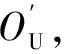
表3 平台构型参数表

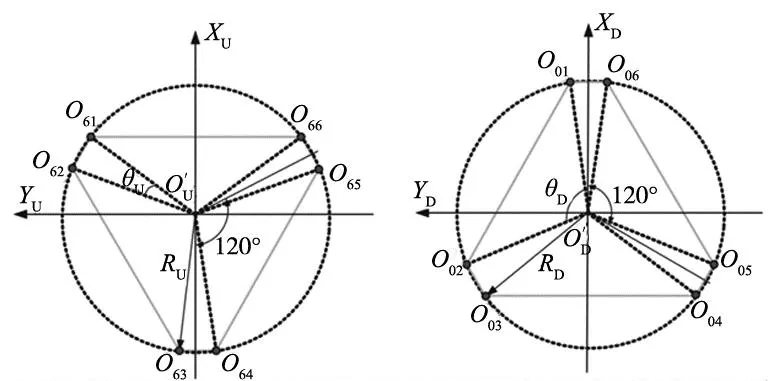
图15 上下铰点分布示意图

动平台连体坐标系OU-XUYUZU在全局坐标系OD-XDYDZD中的空间位置和姿态由六维向量[X,Y,Z,α,β,γ]确定。可得其传递矩阵ODTOU为:

(18)

3.2 铰点坐标的表示

如图16所示,在静平台下铰链下转动中心点O0i(i=1,…,6)处,基于全局坐标系OD-XDYDZD建立6个以点O0i为原点的静平台局部坐标系O0i-X0iY0iZ0i,其中Z轴延铰链转轴方向向外,Y轴平行于静平台台面。同样的如图17所示,基于动平台上台面中心处的动平台连体坐标系OU-XUYUZU建立6个以点O6i为原点的动平台局部坐标系O6i-X6iY6iZ6i,其中Z轴延铰链转轴方向向外,Y轴平行于动平台台面。

图16 下铰链转动中心连体坐标系示意图

在全局坐标系OD-XDYDZD中各个局部坐标系O0i-X0iY0iZ0i的原点O0i位置可以表示为:

ODO0i=[RDcθO0iRDsθO0iHD]T

(19)

式中:

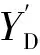
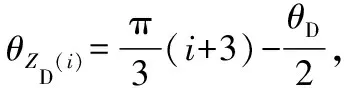
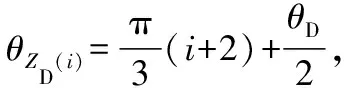
由此可得静平台下铰链下转动中心点的连体坐标系O0i-X0iY0iZ0i与全局坐标系OD-XDYDZD的姿态变换矩阵ODRO0i为:

(20)

从而可得各连体坐标系O0i-X0iY0iZ0i与全局坐标系OD-XDYDZD的传递矩阵ODTO0i的表达式为:

(21)

同理可得各连体坐标系O6i-X6iY6iZ6i与连体坐标系OU-XUYUZU的传递矩阵OUTO6i的表达式为:

(22)

式中:

OUO6i=[RU·cθO6iRU·sθO6i-HU]T

(23)

(24)

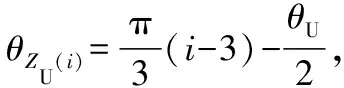
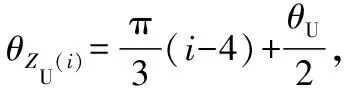
3.3 D-H参数及第i条支腿运动学

采用D-H参数法建立如图18所示的第i个支腿的运动链并建立相应的坐标系定义6-RR-RP-RR并联机构的构型参数。在每个关节变量处设立一个局部坐标系来求解本文中的6-RR-RP-RR并联机器人的逆运动学,它们分别是下铰链下转轴连体坐标系O1i-X1iY1iZ1i(i=1,…,6)、下铰链上转轴连体坐标系O2i-X2iY2iZ2i(i=1,…,6)、支腿转动运动副组件连体坐标系O3i-X3iY3iZ3i(i=1,…,6)及支腿移动运动副组件连体坐标系O4i-X4iY4iZ4i(i=1,…,6),以及上偏置柔性虎克铰链下转轴连体坐标系O5i-X5iY5iZ5i(i=1,…,6)。

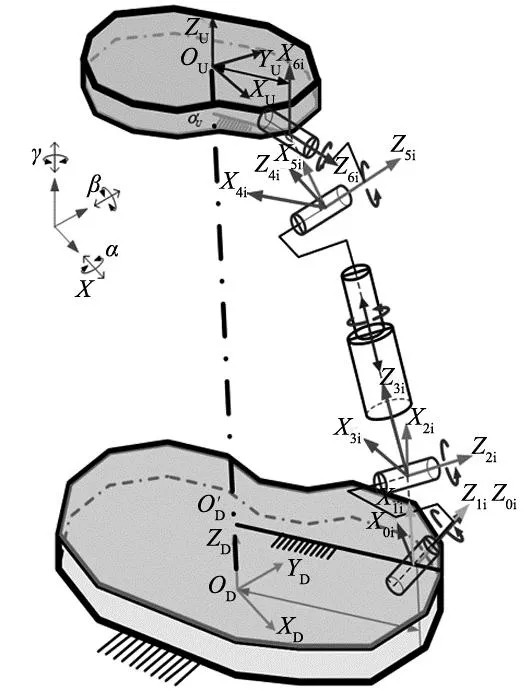
图18 第i条支腿运动链上连体坐标系的定义

由D-H参数模型理论,我们可以得到如表4所示的第i个支腿的D-H参数。

两个相邻坐标系之间的空间位姿关系可以通过式(25)所示的位姿变换矩阵表示。

nTn+1=Rot(z,θn+1)×Trans(0,0,dn+1)×
Trans(an+1,0,0)×Rot(x,αn+1)

(25)

根据D-H表示法,可推导出该并联调整平台第i个支腿运动链,杆件n到最后关节的变换矩阵为:

nT6(i)=nTn+1(i)n+1Tn+2(i)n+2Tn+3(i)…5T6(i)

(26)

3.4 逆运动学求解

该差动式六自由度并联柔性微动机器人的动平台和静平台由6个结构相同且按照一定构型排列的支腿相连接。当给定动平台的位姿时,就可以知道传递矩阵ODTOU,且有式(27)所示关系式为:

O0iTO6i=O0iTOD·ODTOU·OUTO6i=(ODTO0i)-1·ODTOU·OUTO6i

(27)

为了便于书写,记为:

(28)

由于传递矩阵0T6(i)和O0iTO6i相等,即0T6(i)=O0iTO6i,则其两个传递矩阵中相应元素也相等,因此:

Mi=0T6(i)-O0iTO6i=0

(29)

由上述分析可知,该逆运动学问题中,每个支腿对应一个包含12个非线性方程的方程组。在每条支腿的12个非线性方程里面挑选出6个包含所有未知变量的非线性方程组成一个非线性方程组。

本文建立的第i个支腿非线性方程组表达式为:

(30)

由于式(30)所示的非线性方程组没有解析解,所以采用牛顿-拉普拉森数值迭代方法求解,其中支腿中未知变量θ1i、θ2i、L3i、θ4i、θ5i及θ6i可以由如式(31)所示的迭代式计算。

(31)

然后给定初值和计算的误差条件,就可以利用迭代式(31)和初值进行数值计算,求得在满足误差条件下的第i条支腿运动链中所有的未知关节变量θ1i、θ2i、L3i、θ4i、θ5i和θ6i。

4 并联平台运动学仿真

4.1 刚性铰链并联平台运动学仿真

为了验证运动学模型的准确性,首先对基于刚性铰链的整机平台用多体动力学仿真软件进行仿真验证。根据上节建立的运动学理论模型,随机给定上平台的位姿计算出每个支腿的伸缩量,然后将理论计算得到的每个支腿的伸缩量作为驱动施加在对应的丝杠上,启动Adams运动学仿真,就可以得到对应的动平台位姿的仿真结果,整机仿真模型如图19所示,给定位姿与仿真结果的记录在表5。

表5 给定位姿与仿真结果对比

图19 刚性铰链平台仿真模型

4.2 柔性铰链并联平台运动学仿真

将铰链设置为柔性体,其他零部件均设置为刚性体,因此其仿真过程是刚柔耦合体的运动学仿真。将每条支腿中丝杠和驱动件间设置的圆柱副作为驱动,在丝杠上设置延着其轴线方向上的线性位移,对其进行正运动学仿真,整机仿真模型如图20所示,给定位姿与仿真结果的记录在表5。

图20 柔性铰链平台仿真模型

表5中,G为动平台的给定位姿,SR为采用刚性铰链的整机平台动平台的仿真位姿,SF为采用柔性铰链的整机平台动平台的仿真位姿。

由表5可知,当动平台做纯平动运动时,刚性铰链整机平台仿真所得的动平台位姿与理论计算的动平台位姿误差中最大平动相对误差为0.53%,柔性铰链整机平台仿真所得的动平台位姿与理论计算的动平台位姿误差中最大平动相对误差为0.17%,平台运动分辨率为10 μm级别。当动平台做平动和转动的耦合运动时,刚性铰链整机平台仿真所得的动平台位姿与理论计算的动平台位姿误差中最大相对误差为0.63%,柔性铰链整机平台仿真所得的动平台位姿与理论计算的动平台位姿误差中最大相对误差为0.62%,平台运动分辨率为10 μm级别。以上运动学仿真证明了运动学理论模型的正确性,同时也证明了用柔性铰链代替刚性铰链的有效性。存在误差的主要原因是运动学理论模型数值计算中的截断误差和累计误差。

5 结论

本文依托于部门某望远镜预研项目,基于Stewart并联机器人构型和偏置柔性虎克铰链,利用双螺旋副差动传动方案设计了一种六自由度并联微动机器人。对位移驱动腿和整机结构进行了建模设计,并对柔性铰链的结构参数依据所求得的柔度模型进行了优化设计。利用D-H参数方法建立了该平台的逆运动学模型并采用两种运动学仿真方法对其进行了仿真验证。结果表明用该差动方案和柔性铰链设计的六自由度并联平台具有较高运动精度。当动平台做纯平动运动时,柔性铰链整机平台仿真所得的动平台位姿与理论计算的动平台位姿误差中最大平动相对误差为0.17%,平台运动分辨率为10 μm级别。当动平台做平动和转动的耦合运动时,柔性铰链整机平台仿真所得的动平台位姿与理论计算的动平台位姿误差中最大相对误差为0.62%,平台运动分辨率为10 μm级别。