基于声振融合的二次EWT-CNN刀具磨损监测*

郝旺身,娄永威,董辛旻,李继康,娄本池

(郑州大学机械与动力工程学院,郑州 450001)

0 引言

在切削加工过程中,刀具难免会产生磨损和破损,因此,准确识别刀具的运行状态对于保证切削加工的正常进行具有重要的意义[1]。声振融合数据在故障识别方面相对振动或声音数据表现出了更高的识别率。同时在数据预处理方面保留更多的故障信息也是故障监测研究中的重中之重。

黄德福等[2]通过分析噪声功率谱实现钻头磨损状态的实时检测;陈静等[3]结合小波神经网络对切削声信号进行处理,实现刀具磨损状态的识别;张存吉等[4]则使用CNN对振动数据进行分类,实现刀具磨损程度的识别。数据融合的方法主要有数据层融合、特征层融合和决策层融合3种方法。史志远等[5]用数据并联方式将振动信号和声音信号重构为二维信号,并输入CNN进行故障诊断。杨帆等[6]用BP神经网络和D-S证据理论对多种特征信号进行信息融合。YU等[7]使用ASCNN和ESCNN分别对振动信号和声音信号提取局部特征,并基于DS理论对特征信号进行决策融合。WANG等[8]提出的基于1D-CNN的VAF算法,先对振动信号和声音信号进行特征提取,再通过全连接层实现特征融合和分类。数据层融合具有数据信息丰富、精度高的优点,而特征层和决策层融合会损失大量有用信息。陈澄等[9]的实验结果表明,数据层融合是信息量损失最小的,同时准确率也最高。

得到融合信号后的进一步去噪和信息增强对分类效果至关重要。ZHANG等[10]直接将内在模态函数送入卷积神经网络进行特征学习和分类。WANG等[11]利用VMD算法分解PD信号并对固有模态函数进行小波去噪和重构,提高分类准确性。直接输入各分量会将噪声带入训练,影响分类效果。对所有固有模态函数进行小波去噪会滤去故障信号,对分类模型要求更高。

针对上述问题,本文提出一种基于协同过滤融合的方法,对钻头钻削时同时采集到的声音信号和振动信号进行相关性融合,得到声振融合信号。然后对其进行二次EWT,在故障信号频率范围层面完成信号去噪和重构。最后对重构信号进行信号增强并送入卷积神经网络完成特征提取及分类,实现钻头故障类型的精确识别。

1 基本理论

1.1 协同过滤融合

协同过滤(collaborative filtering)是推荐系统中比较常用的一种算法,基于用户或物品之间的相似性,预测用户对未知的物品的评分[12]。而这里的协同过滤融合是指对多个信号之间的频域相关性分析后返回数据层次对其进行融合。具体来说,可以通过如下步骤来实现两组声音数据和振动数据之间的融合,如图1所示。

图1 声振融合数据融合流程

步骤1:将声音数据和振动数据分别表示为时间序列,即将它们在时间轴上的变化转换为数字信号;

步骤2:通过利用傅里叶变换对两组数据分别进行频域特征提取;

步骤3:对两组数据进行相似性分析,得到它们之间的相似性矩阵;

步骤4:利用相似性矩阵来确定合适的权重参数,进而对两组数据进行加权和,得到最终的融合结果。

1.2 经验小波变换理论

EWT方法的原理[13]是先将信号的Fourier谱划分为连续的区间,然后在每个区间上使用小波滤波器组进行滤波,最后通过信号重构得到一组调幅调频分量。该方法可以自适应地提取信号的不同频率成分,并具有紧支撑特性。

(1)EWT频带划分。给定信号f(t),先进行傅里叶变换,得到归一化在2π范围内的傅里叶频谱,根据香农准则,在分析过程中仅讨论[0,π]上的信号特性。因此,将Fourier频谱支撑区间定义在[0,π]内。

假设该信号是由N个单分量成分构成,处理过程中将Fourier谱的支撑区间分割成N个连续段,共有N+1个边界(ωn表示各段之间的边界),其中ω0=0,ωn=π。Fourier轴的分割示意图如图2所示。

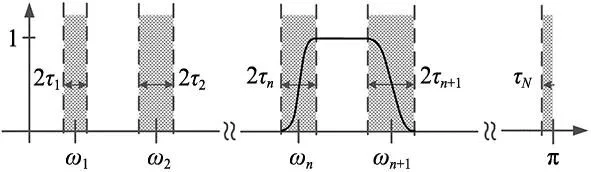
图2 傅立叶轴的划分

每一段的分割可以定义为Λn:

Λn=[ωn-1,ωn],n=1,2,…,N

(1)

很容易得到整段区间存在下面关系:

(2)

在[0,π]内得到一组极大值后,将连续的两个极大值之间的中心定位为每个ωn的边界。对于信号f(t),设前N个极大值在频域内对应的角频率Ωn(n=1,…,N),那么EWT的频带划分边界ωn=(Ωn+1+Ωn)/2。为了方便后续构造滤波器,定义了宽度为Tn=2τn的过渡段(上图中的网格区),这些过渡段都是以边界ωn为中心。

(2)定义经验尺度和经验小波函数。经验小波被定义为每个Λn上的带通滤波器,为此,利用Littlewood Paley和Meyer小波的构造思想,然后对于∀n>0,分别用式(3)和式(4)定义经验尺度函数和经验小波函数。

(3)

(4)

式中:β(x)函数是一个任意Ck([0,1])函数,为:

(5)

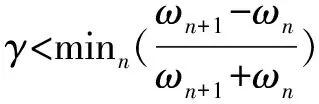
(6)

(7)

则信号f可重构为:

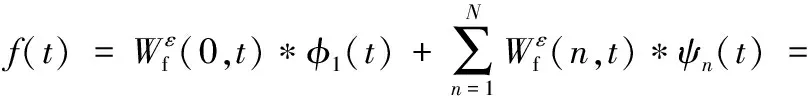
(8)

根据经验小波变换信号f重构公式可得经验模态fk:

(9)

(10)

1.3 卷积神经网络

卷积神经网络(CNN)是一种常见的神经网络,被广泛应用于图像分割、分类、检测和检索等任务中。卷积神经网络最初由HUBEL等[14]在研究猫脑皮层神经元时提出。该网络结构通常包括输入层、卷积层、池化层、全连接层和输出层。

输入层用于输入数据,而卷积层的作用是使用卷积核进行特征提取和特征映射。为了增加非线性映射,需要使用激励函数(RELU)对卷积层的输出结果进行非线性映射。常用的激励函数包括Sigmoid、Tanh、ReLU、ELU和Maxout。卷积层的运算模型可以表示为:

(11)

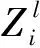
池化层主要进行下采样,对特征数据稀疏处理。这既可以简化网络计算复杂度,也可以提取主要特征减小模型规模,提高运算速度,同时提高所提取特征的鲁棒性。常用的池化函数包括平均池化、最大池化、最小池化和随机池化。其中最大池化的模型表示为:

(12)

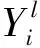
全连接层的作用是将提取的特征组空间拓扑结构展开,进行非线性组合之后以向量形式输出。全连接层的数学模型可以表示为:

(13)

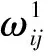
输出层是在全连接层接收上层所有的特征后,将输出值送给分类器。如Softmax分类器。

2 刀具磨损监测流程

基于声音信号、振动信号以及声振融合信号的刀具磨损状态监测,根据所采集信号中所包含的钻头磨损的特征,分别对钻头正常、崩刃、中度磨损、重度磨损4种状态进行监测识别。具体实现步骤,如图3所示。

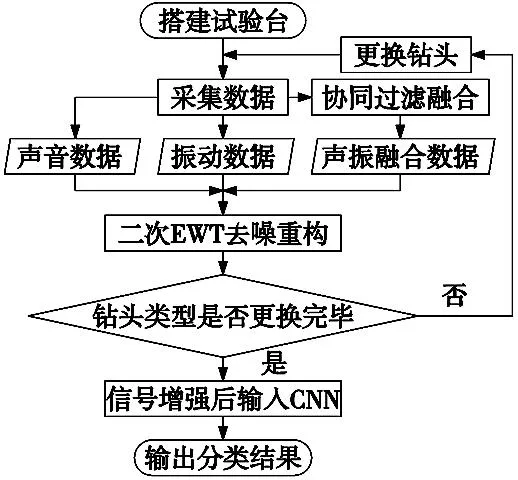
图3 刀具磨损诊断流程图

(1)首先对采集到的原始数据预处理得到钻头不同类型状态的声信号以及振动信号,之后再将对应的声信号以及振动信号通过协同过滤融合,得到一组基于相关性融合的声振信号。

(2)对预处理后得到的声信号、振动信号、声振信号分别进行第一次经验小波变换(EWT)得到其对应的经验模态分量。

(3)对经验模态分量中混杂高频噪声部分再次使用EWT,得到其对应的经验模态分量。

(4)对第二次EWT得到的经验模态分量剔除其噪声部分,并将剩余分量与第一次EWT得到的其余分量加权重构得到重构后的信号。

(5)将重构后的信号增强后分别放入卷积神经网络中进行自动特征提取并对模型进行训练和测试。具体流程细化如图4所示。

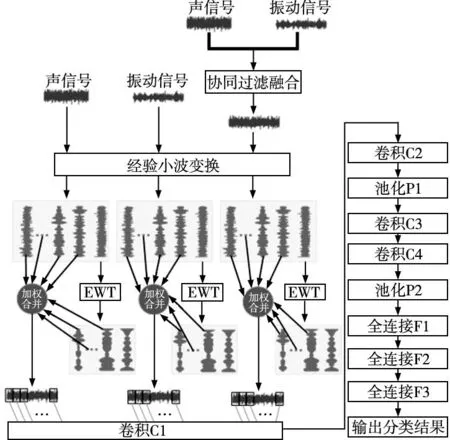
图4 信号处理细化图

3 实验验证

为了验证声振融合信号在刀具故障诊断方面的优越性,通过搭建如图5所示的刀具磨损监测实验台进行数据采集进而对比试验。实验采用一台微型钻床进行钻削工件,该钻床最高主轴转速为2500 r/min,可对其在0～2500 r/min转速范围内进行多档钻速调节,在对工件钻削过程中不使用冷却液,钻削工件选择为厚6 mm的45号钢板材,刀具选择HSS麻花钻头(正常刀具参数直径7.5 mm,钻头总长109 mm,螺旋槽长69 mm,顶角度数118°),为了进行实验对比,钻头共选用(如图5)4种类型:正常、崩刃、中度磨损、重度磨损。钻削过程中声音信号以及振动信号通过由东方所研制的型号为INV3062T0的信号采集系统进行采集,振动信号采用加速度传感器进行采集,通过粘贴双面胶对其进行固定。声音信号通过麦克风传感器进行接收,麦克风传感器固定于水平距离工件钻削处20 cm处。该采集系统可同时采集四通道的信号数据。最后通过以太网传输将信号数据上传到计算机。

图5 试验台及4种钻头类型

首先控制钻床主轴钻速为2400 r/min,控制自动进给。然后依次换用正常、崩刃、中度磨损、重度磨损4种类型钻头进行钻削,每次均对板材的中心位置进行钻削,传感器参数如表1所示。

表1 传感器参数表

在钻头开始接触到工件时开始采样,工件钻孔完成后停止采样。完成主轴转速2400 r/min的钻削过程的采集后,又进行主轴转速为1600 r/min以及主轴转速为2000 r/min的切削过程的数据采样以此丰富实验的对比。在此主要展示主轴转速2400r/min的数据处理以及分析结果。

在控制以上实验参数后,采集完成数据,对数据截取预处理完成可得到4种状态类型钻头下的声信号、振动信号、声振融合信号的时域分析情况如图6所示。

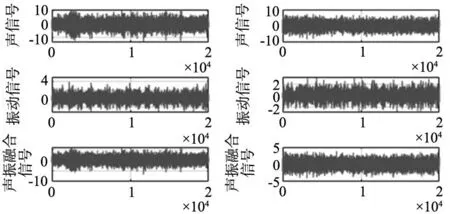
(a) 正常 (b) 崩刃

将上述信号利用经验小波变换进行第一次分解,得到重度磨损类型钻头的声振融合信号分解后的前6个经验模态分量以及其所对应的频谱图如图7所示。由图7中可以看出在分量mra1中依然包含很多高频信号,为了去除高频噪声的影响,进而对分量mra1再次使用EWT进行经验小波变换得到组成mra1的分量中的前6个分量如二次分解图8所示。在二次分解中定义mra1为1-mra1。

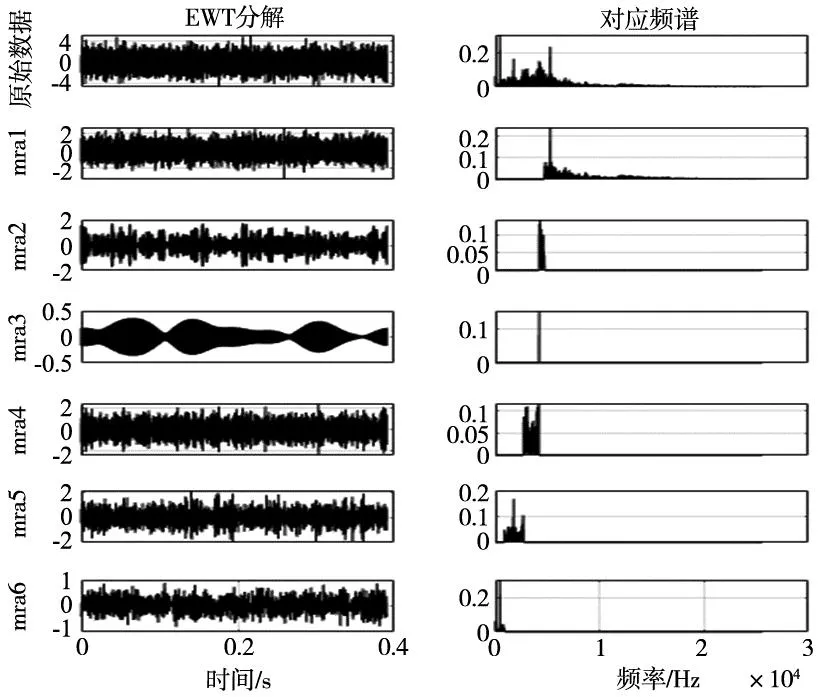
图7 声振信号一次分解

图8 声振信号二次分解

经过二次分解的第一个分量依然包含很多噪声数据,但此分量信息更多包含了超过故障信号频率的高频噪声部分,因此剔除二次分解后的第一个分量,而将第一次分解以及二次分解的其他分量进行加权重构。将二次分解中的高频部分剔除后得到的加权重构信号如图11所示,其中声音信号(图9)和振动信号(图10)的重构过程同声振信号。该重构信号的频率段包含了绝大部分故障频率,之后将该重构数据放入卷积神经网络中对模型进行训练和验证。

图9 重构声信号

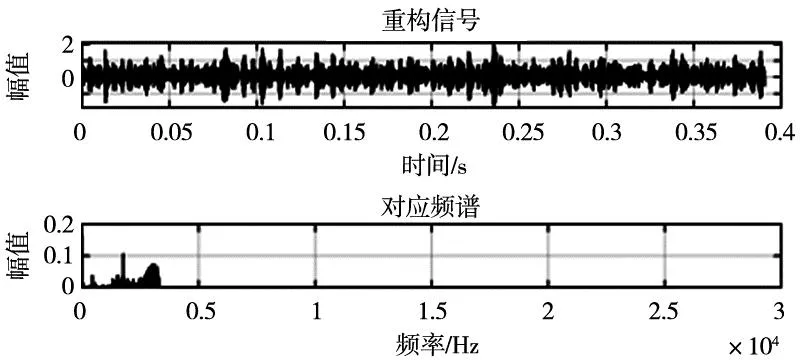
图10 重构振动信号

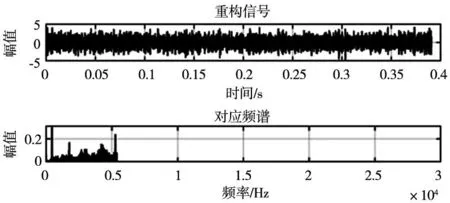
图11 重构声振信号

4 结果分析

本次实验中对模型(表2)的训练以及测试过程选取100轮迭代来观察模型的训练测试情况,截取数据的80%作为训练数据,20%作为测试数据。为了保证实验的准确度,对一组数据进行5次运行并取其平均值作为训练以及测试结果。图12b中测试损失函数值随着迭代次数增加,前期大幅减小后经小幅波动均得到较小值。说明该模型在测试数据集上的预测误差小,泛化能力强。进而保证了3组数据在该模型测试阶段表现出高准确率的可信度。

表2 网络结构参数

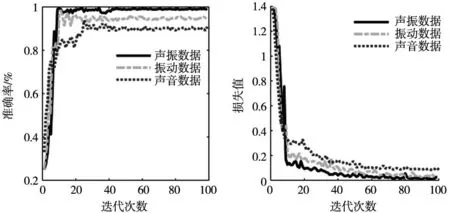
(a) 测试准确率 (b) 测试损失函数

而且从图12a测试准确率中可以看出振动数据和声振数据在迭代13次后波动大幅减小,而声音数据在迭代26次后开始趋于稳定,最终可以明显看出声振融合数据的准确率最高,趋于稳定的平均值为98.96%。为了增加对比实验,本实验又将二次EWT分解-CNN和一次EWT分解-CNN以及CNN进行了对比测试。测试结果如图13所示。

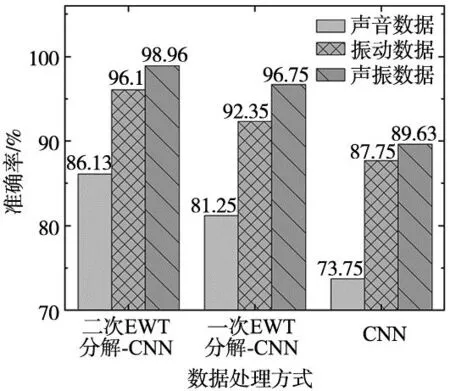
图13 对比试验准确率

从图13可以看出,经本文提出的融合方法得到的声振数据在钻头故障识别准确率上明显优于单一振动数据和单一声音数据。相比传统的对原始信号一次EWT分解再挑选分量重构或者直接原始数据送入CNN进行故障识别,经二次EWT分解去噪重构信号结合CNN进行故障识别准确率明显更高。

5 结论

本文针对麻花钻头的正常、崩刃、中度磨损、重度磨损4种类型钻头的钻削工作进行磨损识别实验。

(1)本文所提出的二次EWT分解-CNN刀具磨损识别方法在与传统识别方法的对比实验中以高达98.96%的识别准确率突出优势。

(2)通过将声振融合信号与传统振动信号和声音信号进行对比实验,证明了声振融合信号包含的故障信息更全面,识别精度更高。

(3)将钻头故障频率范围内的经验模态分量进行重构后得到的重构信号在CNN识别中表现的高准确率,说明了针对故障频率范围的去噪能够保留更多的故障信息。