三移一转并联机构运动学分析*

陈会元,王 蕊,张明泽,武海军,张金柱

(太原理工大学机械与运载工程学院,太原 030000)

0 引言

钢铁搬运行业大多采用传统工业机器人,即串联式机构,来实现对钢铁的空间位置输送,以及水平姿态的调整。在此类工业应用中,机器人需要保证一定的承载能力,以及拥有较大的刚度。

并联机构具有高刚度、高速、高精度、力学性能好等优势[1-2]。在短距离搬运作业中,三移一转并联机构具有一定的适用性。

目前,对于并联机构的研究,在运动学领域不断深入。冯志坚等[3]推导出三自由度并联机构的位置解,并进行了工作空间求解。江小辉等[4]对TriMule机器人进行了运动学正反解。张春燕等[5]对4-URPU并联机构进行了运动学分析和优化。对于机构的研究普遍会着手于运动学,比如自由度以及位置解,而针对于不同的机构,解法上存在不同。

LU等[6]提出一种新的研究工作空间方法-CAD变量几何法。此方法仅仅依赖于对杆件的约束,不需要建立数学模型,具有一定的便捷性。吴存存等[7]对2PPPaR并联机构进行了位置求解和工作空间分析,GOSSELIN等[8]求解出了4PRRU(Quadrupteron)机构工作空间体积,此类机构均采用滑轨驱动,其工作空间体积较大,而由于滑轨占地大,在局部搬运作业中会受到一定限制。

机器人机构由运动副与杆件按照一定方式连接而成[9]。在诸多并联机构中,执行支链采用平行四边形铰链,可以约束末端动平台的转动自由度[10-11],那么在构型上就有了新的结构设计思路。平行四边形铰链是一种封闭环结构,相对于单链机构有较大的刚度。而目前对可以实现三移一转的含有双平行四边形铰链的机构的研究较少。

本文针对钢铁搬运任务需求,提出一种具有较大刚度的含有双平行四边形铰链的新型三移一转并联机构,建立了位置反解数学模型,并进行了轨迹规划研究,同时验证了位置反解的正确性,采用PID控制器实现了机构位置的精确控制,采用CAD变量几何法得出了机构的工作空间。

1 运动学分析

提出新型三移一转并联机构,包括静平台、动平台和3条分支,本机构采用移动副作为输入,动平台作3维移动和绕竖直方向的转动。并联机构简图如图1所示,每条分支由驱动支链RPR和执行支链RPaPaR组成。在第i(i=1,2,3,4)条驱动支链中,转动副Ri1和Ri2分别为支链上下两端的转动副,移动副为Pi。特别地,第一条分支有两条驱动支链,其余两条分支均只有一条驱动支链。在第i(i=1,2,3)条执行支链中,转动副Ri0和Ri9分别为支链上下两端的转动副,6个转动副Ri3、Ri4、Ri5、Ri6、Ri7和Ri8构成两个平行四边形铰链Pai1和Pai2。

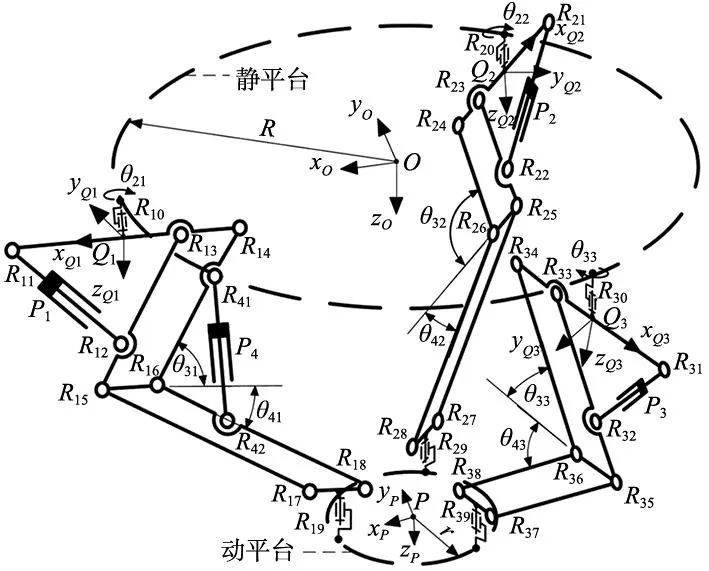
图1 并联机构简图

1.1 建立坐标系

如图1所示,建立基坐标系{O}:选取静平台质心点O为原点,xO轴方向为点O水平指向静平台上的点Ri0(i=1,2,3);建立动坐标系{P}:选取动平台质心点P为原点,xP轴方向为点P水平指向动平台上的点Ri9;建立连杆坐标系{Qi}:选取杆Ri1Ri4质心点Qi为原点,xQi轴方向为点Qi水平指向点Ri1,zO轴、zP轴和zQi轴方向均为竖直向下(i=1,2,3),yO轴、yP轴和yQi轴由右手定则确定。设置点Ri0与杆Ri1Ri4质心点Qi距离为0,杆Ri9与杆Ri7Ri8质心点距离为0。定义θ1i为向量OQi与xO轴的夹角,根据i依次取0°、120°和-120°。设l1、l2、l3和l4分别为杆Ri1Ri4、杆Ri5Ri6、杆Ri3Ri5和杆Ri5Ri7的长度;l5和l6分别为点R41到R16的距离和点R42到R16的距离。

1.2 自由度分析

第一分支旋量系统图如图2所示,P1、R10～R12、R19、R41、R42和P4的螺旋分别对应＄1、＄10～＄12、＄19、＄41、＄42和＄4,R13～R16及R15～R18均等效为平行四边形铰链,分别对应的螺旋为＄13及＄14。在坐标系{Q1}:Q1-xQ1yQ1zQ1下,包含驱动支链和执行支链的第一分支的运动螺旋为:

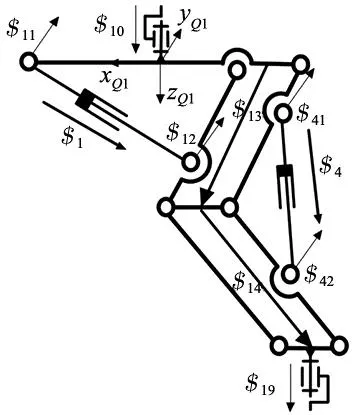
图2 第一分支旋量系统

＄1=(0 0 0;d10f1)
＄10=(0 0 1;0 0 0)
＄11=(0 1 0;0 0l1/2)
＄12=(0 1 0;d120f12)
＄13=(0 0 0;d130f13)
＄14=(0 0 0;d140f14)
＄19=(0 0 1;0e100)
＄4=(0 1 0;d40f4)
＄41=(0 1 0;d410f41)
＄42=(0 1 0;d420f42)

(1)

式中:d、e、f均为实数。

由式(1)得到第一分支的反螺旋为:

(2)

同理,与式(1)类似,第二和第三分支不包含＄41、＄42和＄4,可得第二和第三分支分别在坐标系{Q2}:Q2-xQ2yQ2zQ2和{Q3}:Q3-xQ3yQ3zQ3的反螺旋也为:

(3)

(4)

每个分支都对动平台作用一个约束力偶,这3个约束力偶分别与转动副R19、R29和R39垂直,它们都平行于动平台平面。此时,在坐标系{P}:P-xPyPzP下,动平台的含3个螺旋的约束螺旋系可以表示为:

(5)

(6)

(7)

式中:j和k均为实数。

由于这3个螺旋都具有相同位置的4零元素,可以确定这3个螺旋共面因而它们线性相关,只相当于两个独立的约束,因而其中有一个为虚约束。它们的二次反螺旋＄rr即为我们要找的确定的动平台自由度性质的动平台运动螺旋＄pm。

(8)

(9)

(10)

(11)

依据动平台运动螺旋可以确定动平台具有的4个自由度,分别为3个移动自由度和1个绕Z轴的转动自由度。

1.3 位置逆解

在基坐标系{O}下,已知动平台的位移参数X、Y、Z以及绕Z轴的转动角φ,求驱动杆Ri1Ri2的长度Hi(i=1,2,3,4)。sin简化为s,cos简化为c。定义运算:

(12)

点Ri0在{O}中可表达为(i=1,2,3):

(13)

点Ri9在{O}中可表达为(i=1,2,3):

(14)

点Ri9在{Qi}中可表达为(i=1,2,3):

(15)

点Ri9在{O}中也可表达为(i=1,2,3):

(16)

(17)

由式(14)和式(16)相等,得:

(18)

(19)

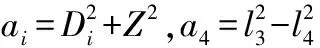
(20)

对ΔRi1Ri2Ri3(i=1,2,3)与ΔR41R42R16使用余弦定理得驱动杆的长度Hi(i=1,2,3,4):

(21)

(22)

2 轨迹规划与验证

2.1 轨迹规划

仿真实例中所用的杆件参数值如表1所示。

表1 杆件的参数值

本节的目的是将动平台按照规定轨迹运动,并研究驱动杆的运动规律。先将已经绘制好的机构的Solidworks三维模型另存为.x_t格式,导入仿真软件ADAMS中。并创建好杆件之间的约束,点击仿真分析,验证模型,模型正确。

动平台携带抓取装置,根据钢铁搬运任务需求,需要动平台由初始位置A,到达抓取位置B,抓取物体后运输到投放位置C,投放物体后到达抓取装置维护位置D,维护完成返回初始位置A,期间需要动平台做出相应的姿态调整。设置位移与角度的单位分别为mm和°。

点A位姿为[XYZφ]=[-5.5 12.8 110 -15.2],点B位姿为[10 20 130 -5],点C位姿为[15 -10 120 -20],点D位姿为[-2 -15 135 -10]。轨迹为A→B→C→D→A,分为4个阶段,在每个阶段,动平台的4个自由度方向均需添加一个驱动。限制质心在每个阶段,动平台起始速度及加速度为0,终止速度及加速度为0,各阶段运动时间为1 s,总共4 s。

已知质心在每个阶段的始末位姿,设五次多项式为f(t)=c5t5+c4t4+c3t3+c2t2+c1t+c0,ci(i=0,1,2,3,4,5)为待定系数,通过式(12)被求解出。

(23)

式中:t0=0,t1=1,x0与x1分别取每个阶段对应X、Y、Z和φ方向的起始值和终止值,[x0x1]按阶段依次取如下数值:

第一阶段:[-5.5 10]、[12.8 20]、[110 130]、[-15.2 -5];

第二阶段:[10 15]、[20 -10]、[130 120]、[-5 -20];

第三阶段:[15 -2]、[-10 -15]、[120 135]、[-20 -10];

第四阶段:[-2 -5.5]、[-15 12.8]、[135 110]、[-10 -15.2]。

由于软件中的模型已在初始位姿点A,所以对每个方向求解出的c0项均需减去点A对应的的初始值后代入。对应X、Y、Z和φ方向的有关位移的五次多项式驱动函数的系数按照阶段次序依次在表中排列,如表2所示。

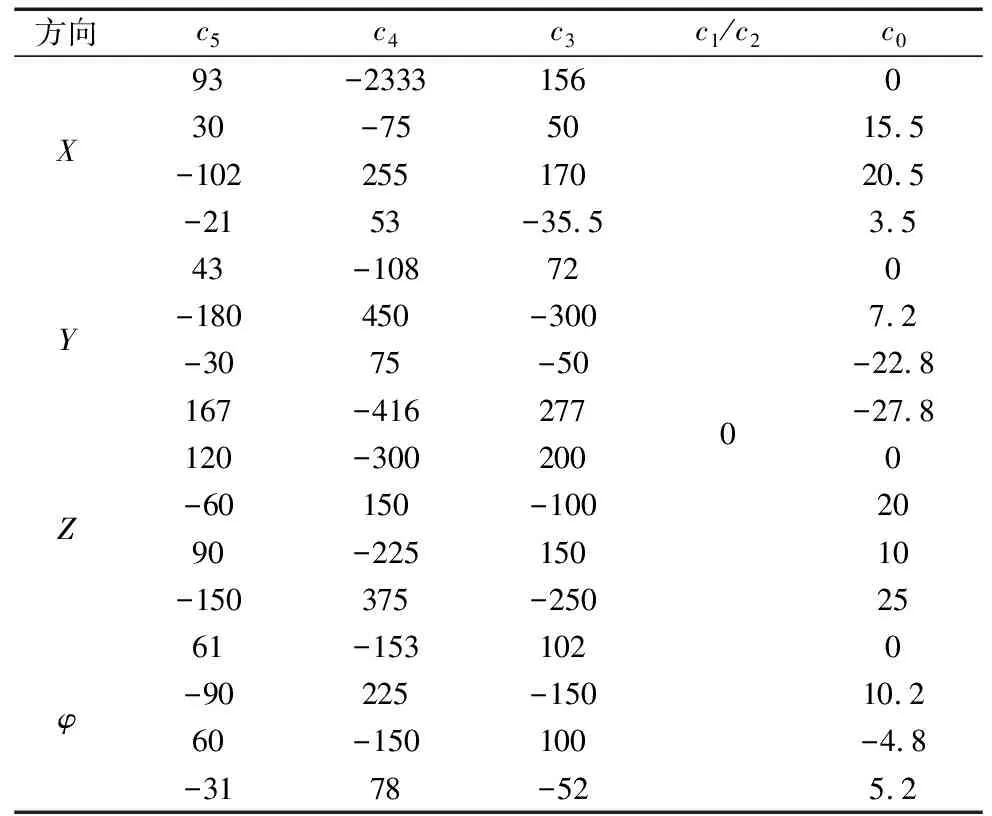
表2 驱动函数系数

在ADAMS中完成上述运动学仿真,将动平台质心点运动数据导入MATLAB,并进行绘制,得到动平台质心由A→B→C→D→A的运动轨迹以及动坐标系的变化如图3所示。

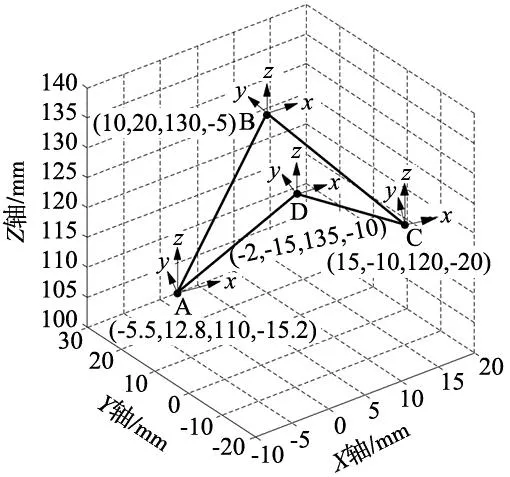
图3 动平台运动轨迹图

驱动杆的运动情况如图4所示。

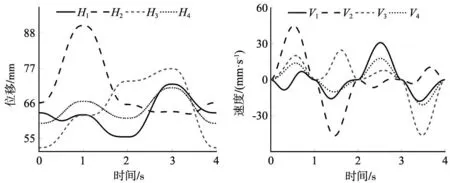
(a) 位移曲线 (b) 速度曲线

由图4可知,驱动杆的运动曲线光滑,没有突变,说明运动状况正常,该轨迹可以实现。

2.2 位置验证

由ADAMS导出上述运动过程中动平台的位姿以及驱动杆的长度值(即实际值)到MATLAB中,已知动平台位姿,在MATLAB中得到理论位置反解数学模型的计算值(即驱动杆的理论值),并将理论值减去实际值,得到两者的误差如图5所示,最大误差为2×10-3,远小于实际值,由此得出驱动杆的位置逆解数学模型正确。

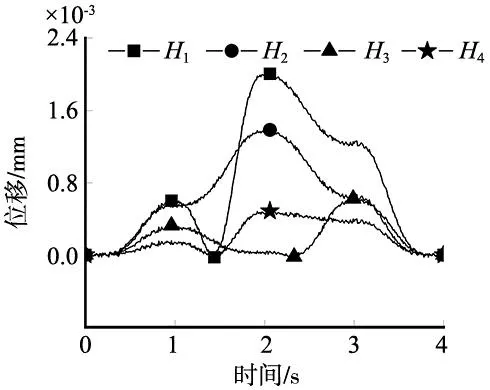
图5 驱动杆位移误差图

3 位置控制

在实际应用需求中,需要实时反馈动平台的实际位置,保证动平台按照预定轨迹运动。本文采用PID控制器来实现对机构的模拟控制,将ADAMS机械系统模型导出,在MATLAB/Simulink中完成控制系统的搭建工作,控制系统框图如图6所示。

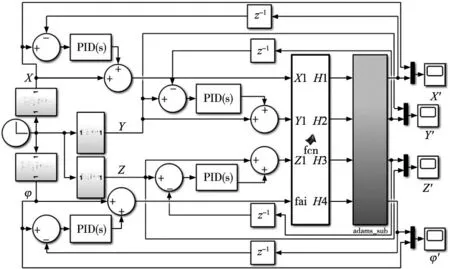
图6 PID位置控制系统

在图6中,主要有时间模块、多项式模块、Sum模块、PID模块、Fcn模块(位置反解数学模型)、机械系统模块、示波器以及delay模块。控制系统的原理为,由时间作为输入信号,将上文动平台轨迹规划的X、Y、Z和φ方向的驱动函数应用于输入中,以此作为位置反解数学模型的输入,求解出驱动杆的位置参数,传输到ADAMS导出的机械系统模型中,从而驱动机构得到动平台的实际位置,并将理想与实际位置的误差经过PID控制器的调节作用到输入信号中,以确保输入与输出一致。

PID参数采用手动调节,以达到效果最佳,其各项参数如表3所示。最终得到动平台实际与理论位置如图7所示。由图7可知,动平台4个方向的位移曲线通过PID调试后与预期轨迹规划的曲线一致,因此该方法是可行的。

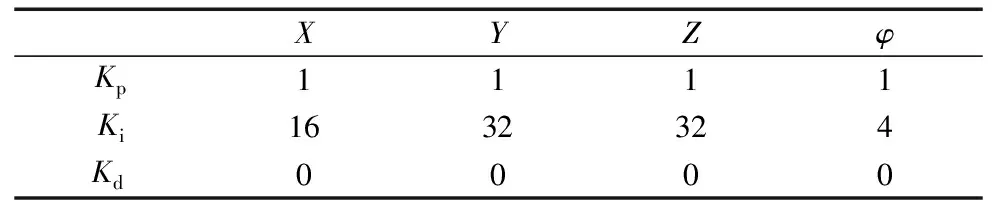
表3 PID参数

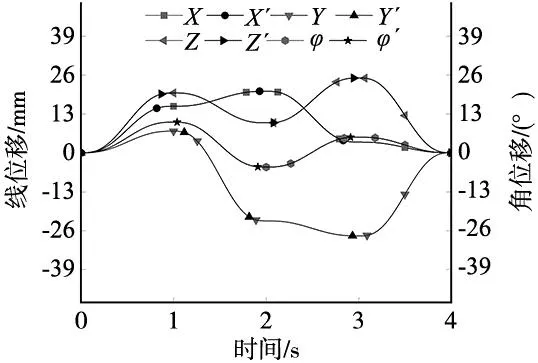
图7 动平台实际与理论位置对比

4 工作空间

机器人的工作空间是机器人操作器的工作区域,它是衡量机器人性能的重要指标。本文采用作图法-CAD变量几何法对该并联机构的可达工作空间展开研究,该方法是通过改变驱动杆长来确定动平台的位置,可看做求正解的过程。

参考图1机构简图,在SolidWorks三维软件中完成三维草图搭建,根据关节运动副,建立约束。采用“锁三驱一”原则,该并联机构有4个线性驱动,保证3个驱动杆长度不变,驱动一个杆,进而生成动平台中心点的运动轨迹线,多条轨迹线可以形成一个面,再由多个面相交,进而选取最外层的面作为包络面,由多个包络面构成的三维空间,即为工作空间。

H1～H4变化范围为50～90 mm,杆长增量为δH=10 mm。定义ni为Hi(i=1～4)由小到大的变化次数,nimin=0,nimax=(Himax-Himin)/δH,H1max=H2max=H3max=H4max=4。

获得工作空间的步骤如下:

步骤1:H1=H1min,H2=H2min,H3=H3min,H4=H4min+n4δH(n4=0,1～4),n4从0变化到4,记录动平台中心点P在{O}中的坐标,将所有的坐标值保存为text文件,并命名为A.txt;

步骤2:在SolidWorks选择插入/曲线/通过XYZ点的曲线命令,浏览文件A.txt,便生成一条空间曲线;

步骤3:H1=H1min+n1δH(n1=0,2～4),H2=H2min+n2δH(n2=0,2～4),H3=H3min+n3δH(n3=0,2～4),H4=H4min+n4δH(n4=0,1～4),H1、H2和H3的组合方案共有n1×n2×n3=125种,每选取一种组合方案,n4从0变化到4,共循环125次,得到125条曲线;

步骤4:连接最外侧曲线上的端点得到边界曲线A1A2A3A4A5A6,B1B2B3B4B5B6,B1C1C2C3B4和B6C5C2C4B2。使用边界曲面命令将这些曲线生成曲面,便获得工作空间如图8所示。

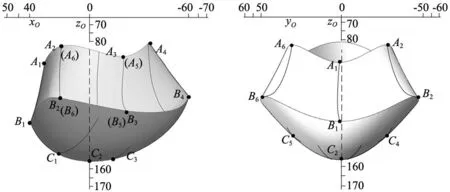
(a) 主视图 (b) 侧视图

图8中边界轨迹线与边界点对应的驱动情况为:

A1B1:H1=50,H2=90,H3=90
A2B2:H1=60,H2=90,H3=50
A6B6:H1=60,H2=50,H3=90
A3B3:H1=90,H2=50,H3=60
A5B5:H1=90,H2=60,H3=50
A4B4:H1=90,H2=50,H3=50
C1:H2=90,H3=90,H4=70
C2:H1=90,H2=90,H3=90
C3:H2=90,H3=90,H4=90
C4:H2=80,H3=50,H4=70
C5:H2=50,H3=80,H4=70

在操作过程中,注意到存在奇异的情况,如图8中所示虚线条所在的位置,即H1=90,H2=90,H3=90(对应X=0,Y=0,φ=0)的情况,在实际应用中应避免出现。工作空间围绕平面xOzO对称,这与并联机构的第二和第三分支围绕平面xOzO对称的结构设计有关。从俯视图可以看出,工作空间是一个近似等边三角形的轮廓,在圆周方向均有分布,由此,该机构可进行多角度作业。工作空间的底部趋向于接近一个点。通过对软件中建立的草图观察,在工作空间允许的范围内,动平台的旋转角度φ最大为±50°,而且动平台位置不同,可旋转的角度范围有所不同。工作空间整体是个不规则体,经过SolidWorks软件计算,工作空间的体积为5.573×105mm3。

定义安装空间为包络该机构的一个圆柱体空间,该圆柱体的半径为r0+100/2=165 mm,高为150 mm,所以该圆柱体空间的体积为π×1652×150=128×105mm3,因此该机构的工作空间与安装空间的比值为5.573/128=0.043 5,与三移一转并联机构Quadrupteron的比例(0.042)相比,比较相近,后续需要对此机构进行杆件参数优化,进而提升工作空间体积。

5 结论

针对钢铁行业搬运需求,提出一种具有双平行四边形铰链的新型并联机构,利用螺旋理论求证出该机构可以实现三移一转,并对其进行运动学分析,完成了位置反解数学模型的求解。根据钢铁搬运任务需求,对机构进行轨迹规划,满足动平台起止时刻速度与加速度为0,通过仿真得到驱动杆运动曲线,其光滑连续没有突变,并验证了位置反解数学模型的正确性。采用PID控制器,完成了控制系统的搭建,确保动平台的实际轨迹与理论轨迹一致,实现了位置控制。采用CAD变量几何法,得出了该机构的工作空间,计算出了工作空间的体积,并与Quadrupteron机构进行了对比;工作空间在圆周范围内分布,有利于多角度作业,而且应尽量避免中心奇异位置。该机构在钢铁搬运行业有一定的应用价值,并为三移一转并联机构研究提供了参考。