基于神经网络优化模型的中药复方安慰剂配色模拟研究

李航,黎盛强,周恩丽,王团结,章晨峰,张欣,肖伟,,王振中,

(1.南京中医药大学康缘中药学院,江苏 南京 210023;2.中药制药过程控制与智能制造技术全国重点实验室,江苏 连云港 222001;3.江苏康缘药业股份有限公司,江苏 连云港 222001)

安慰剂又称模拟剂,指不具有药理活性,在外观、颜色、气味、味道等方面与实验用药物相同或基本接近的制剂,常用于临床试验研究[1]。中药复方制剂的化学成分复杂,具有独特的气味、色泽和口感,通常采用多种色素、辅料和矫味剂进行处方筛选试验,以人工评价打分的方式进行评价,主观性强,很难达到模拟剂的质量要求[2]。

计算机配色技术的发展已有二三十年的历史,各种配色理论和算法都在不断地被提出,并逐渐在印染、涂料、油墨以及塑料着色行业中应用。其最大的意义在于以数字描述颜色,把配色和颜色评价这一传统的匠人技艺上升为科学技术,使得我们可以借助于现代计算机技术来处理生产中遇到的颜色问题,使传统的处方筛选和人工评价方式逐渐向现代的计算机配色和仪器评价方式过渡。邓晓刚提出了基于分区域改进粒子群算法优化的反向传播(Back propagation,BP)神经网络模型[3],很好地改善了传统油墨配色中精度低、过程繁琐和配色理论计算量繁杂的问题。代献泽基于粒子群优化的BP神经网络和计算机视觉设计了一套胶囊配色系统[4],解决了人工胶囊配色主观性强、工作效率低和配色效果难以保证等问题。

BP神经网络是一种按误差逆传播算法训练的多层前馈神经网络,具有较强的非线性映射能力、自适应和容错能力,可以通过学习找出输入与输出之间的规律,适合于解释变量之间的复杂关系[5]。由于BP神经网络依赖于网络的初始值和阈值,且存在训练时收敛速度慢、易陷入局部极小值的缺点,因此出现了确定连接权值和阈值的优化算法[6]。其中,粒子群优化算法(Particle swarm optimization,PSO)是由James Kennedy和Russell Eberhart建立的一种全局搜索算法,不存在局部收敛问题;跟其他智能优化算法相比,算法结构相对简单,且易于实现,收敛速度比较快,且其最广泛的应用范围就是参数优化[7-8]。利用粒子群算法代替BP网络中梯度下降法,可以更好地优化BP网络各层间的连接权值和阈值[9]。

综上所述,本研究选择中药安慰剂模拟中常用的柠檬黄、亮蓝、苋菜红、焦糖色4种着色剂添加的质量分数作为输入,以制备的安慰剂样品颜色参数L、a*、b*值作为输出,构建BP神经网络模型;使用PSO算法优化BP神经网络的初始权重和偏置,使BP神经网络跳过陷入局部极值的陷阱;通过采用线性递减惯性权重法和引入变异算子提高粒子群算法的全局寻优能力,进一步降低模型的误差,提高模型的鲁棒性。从而实现对中药安慰剂颜色的快速模拟,解决安慰剂颜色模拟制备中着色剂添加配比盲目的问题。

1 材料

1.1 仪器

NH300型色差仪及多功能测试组件,深圳市三恩时科技有限公司;Mettler Toledo AL204型电子分析天平,德国梅特勒公司;KQ500DB型数控超声波清洗仪,昆山超声仪器有限公司;标准筛(18目),绍兴市上虞纱筛厂;DHG-9145A型电热鼓风干燥箱,上海一恒科学仪器有限公司;XY-105MW型卤素水分测定仪,常州市常运电子设备有限公司。

1.2 试药

糊精(批号:220301),曲阜天利药用辅料有限公司;柠檬黄(批号:12121009)、亮蓝(批号:10816003),上海染料研究所有限公司;焦糖色DS-001型(亚硫酸铵法,批号:2022101302),潍坊恒泰食品有限公司;苋菜红(批号:11725006),杭州林峰食品添加剂有限公司;芪葛颗粒(批号:230302)、运脾化痰通窍颗粒(批号:221001)、小柴胡颗粒(批号:230807),均取自江苏康缘药业股份有限公司;纯化水,自制。

2 方法与结果

2.1 安慰剂制备

称取糊精适量,分别加入一定质量分数的柠檬黄、苋菜红、亮蓝、焦糖色着色剂溶液,使糊精与着色剂总和为50 g,另加少量水,搅拌均匀,制备软材,过18目筛制成湿颗粒,置于烘箱(105 ℃)中干燥2 h,使得颗粒含水量低于5%(快速水分测定仪测定,温度105 ℃),制得含不同质量分数着色剂的安慰剂样品。

2.2 安慰剂色度测量方法

光源:LED蓝光激发;传感器:光电二极管阵列检测器;测量口径:8 mm;测量条件:CIE 10°标准观测者;光源:D65。

仪器校正后,将制备的不同安慰剂样品颗粒放置于比色皿中测定,测定6次,记录样品颜色参数L、a*、b*的平均值。

2.3 模型预测指标

对模型进行精度检验,选择的指标包括:决定系数(R2)、平均绝对百分比误差(MAPE)[10]、均方根误差(RMSE)[11]。以上评价指标的计算公式如下:

(1)

(2)

(3)

2.4 色差计算及评价

CIE在各行业色差公式的基础上,于1976年正式提出CIELab色差公式[12]。CIELab色差公式提出的颜色评价指标ΔE能较好地反映标样和测试样之间的颜色差异,也满足人视觉器官对颜色变化的感知。

假设标样在CIEL*a*b*颜色空间中表示为(L0,a0*,b0*),测试样为(L1,a1*,b1*),相关计算公式如下[13]。

明度差:

ΔL=a1*b0*

(4)

色度差:

(5)

总色差:

(6)

式中:a*表示红绿间的色度范围,b*表示黄蓝间的色度范围,a*,b*∈[-128,127],L*表示明度,数值介于0～100之间。

文献报道安慰剂与模型药物相似性的评价多数为人工打分法[14],本研究采用CIELab颜色系统的判断标准进行客观评价。ΔE是实测值与预测值之间颜色差异的综合评价指标。表1表示目视色差感受与色差单位的对应关系。

表1 色差感受

2.5 实验数据获取

2.5.1 着色剂样品制备与颜色测定结果 经前期预实验发现,使用柠檬黄、苋菜红、亮蓝、焦糖色4种着色剂可以模拟出大部分中药复方制剂颜色,因此选用上述4种着色剂进行实验。

称取基质辅料糊精50 g,共135份,按照“2.1”项下方法进行样品制备,制备一系列单一着色剂样品和混合着色剂样品,按照“2.2”项下方法对着色剂样品进行颜色参数测定,记录着色剂样品颜色参数L、a*、b*值,部分结果见表2。

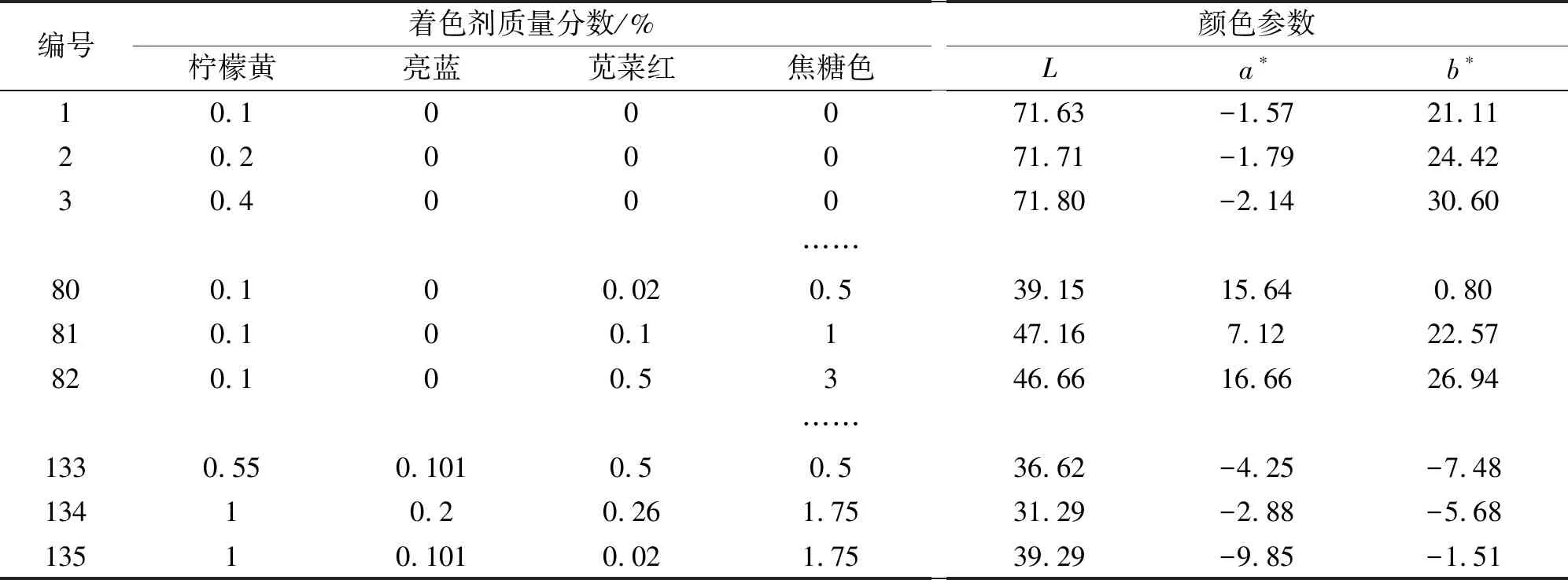
表2 部分着色剂样品颜色测定结果

2.5.2 实验数据预处理 如果数据中某个特征的方差远大于其它特征的方差,那么它将会对算法学习产生很大的影响,使配色模型不能很好地学习其他特征,进而使网络模型失去预期的效果,这将导致最后的模型收敛速度慢甚至不收敛。因此,需要对这样的特征数据进行归一化处理,具体参考公式(7):

(7)

式中,X′:数据归一化后的结果;X:没有归一化的数据;Xmin输入数据中最小的数;Xmax输入数据中最大的数。

2.6 BP神经网络隐藏层参数确定

神经网络权值和偏置的数量取决于网络各层的节点个数,其中神经网络的输入层为4种着色剂质量分数,输出层为着色剂样品L、a*、b*值,隐藏层节点数则需要通过实验获得。选取“Tansig”作为输入函数,“purelin”作为输出函数。选取“trainlm”作为训练函数。最大训练次数为1 000,期望误差为0.000 1,学习率为0.01。隐藏层大致范围采用经验公式(8)[15]结合训练实际情况来确定:

(8)

式中,q为隐藏层的节点个数,m为输入层的节点个数,n为输出层的节点个数;开根号之后结果向上取整,a为调节常数,a在1～10之间取整数,所以q的值为4～13。

将135组样本数据随机打乱顺序,前120组作为训练集,其余15组作为测试集。对神经网络隐藏层分别在4～13范围内依次进行20次实验,训练结果的平均值如表3所示。通过比较网络的MAPE、RMSE、ΔE,结果显示隐藏层节点数为12、13层时网络模型的效果较好,但隐藏层节点数为13层时,会出现过拟合的情况,因此本文将神经网络的隐藏层节点数设定为12。

表3 不同节点数的训练结果

2.7 BP神经网络初始权重和偏置优化

基于BP神经网络收敛速度慢、容易陷入局部极小值等问题,选取不同的全局优化算法对神经网络的初始权重和偏置进行优化。各算法的原理不同,导致不同算法之间各有优缺点。通过对比不同优化算法优化的BP神经网络的训练结果,选择最合适的优化算法。

2.7.1 粒子群算法优化 粒子群算法是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解[16]。假设在一个D维的目标搜索空间中,有N个粒子组成一个群落,其中第i个粒子表示为一个D维向量:Xi=(xi1,xi2,…,xiD),第i个粒子的“飞行”速度也是一个D维的向量,记为:Vi=(vi1,vi2,…,viD),i=1,2,…,N。在第t代的第i个粒子向第t+1代进化时,根据公式(9)、公式(10)更新自身的位置和速度,产生新的种群[17],即:

vij(t+1)=wvij(t)+c1r1(t)[pij(t)-xij(t)]+c2r2(t)[pgj(t)-xij(t)]

(9)

xij(t+1)=xij(t)+vij(t+1)

(10)

式中,粒子i第t次迭代时速度矢量与位置矢量分别为vij(t)和xij(t),i=1,2,…,N,j=1,2,…,D;pij(t)和pgj(t)为个体最优解和全局最优解;c1和c2为加速因子;r1和r2为[0,1]之间的随机数;w为惯性权重。

粒子群算法的相关参数设置为:最大寻优迭代次数为30,种群规模为10,粒子边界为[-1,1],学习因子c1=c2=4.494,粒子运动速度为[-1,1],适应度函数z定义为所优化的BP神经网络的误差值:

(11)

式中,N为训练集总样本数,M为神经网络输出神经元个数;f(xij)为第i个样本的第j个输出节点的可靠度预测值;yij为第i个样本的第j个输出节点的可靠度实际值。

2.7.2 改进的粒子群算法优化 采用线性递减惯性权重法[18]和引入变异算子[19-20]可以提高粒子群算法的全局寻优能力,具体如下。

线性降低权系数:一个较大的惯性权重有利于全局搜索,一个较小的惯性权重有利于局部搜索。在搜索初期需要更大的惯性权重来增强全局搜索能力,更大可能遍历解空间,避免陷入局部最优。搜索后期需要更小的惯性权重增强局部搜索能力,更大可能锁定最优解。wt表示迭代t次后的惯性权重:

(12)

其中,经验值一般取wmax为0.9;wmin为0.4;Tmax为最大迭代次数。

变异算子:是为了让粒子种群变异,产生突变,实现局部搜索收敛加快。pos=unidrnd(numsum),pos是种群发生变异的位置,unidrnd是一个函数,用来产生随机整数。numsum是粒子长度。

2.7.3 遗传算法优化 遗传算法(Genetic algorithm,GA)起源于对生物系统所进行的计算机模拟研究,是一种随机全局搜索优化方法,通过随机选择、交叉和变异操作,一代一代繁衍进化,最后收敛到一群最适应环境的个体,从而求得问题的最优解。GA-BP的模型参数在BP神经网络模型的基础上,遗传算法的相关参数设置为:最大寻优迭代次数为40,种群规模为10,选择方式选择goat工具箱中的几何规划排序选择(normGeomSelect=0.09),交叉方式选择goat工具箱中的算术交叉函数(arithXover=2),变异方式选择goat工具箱中的非统一变异函数(nonUnifMutation=[2 gen 3]),优化变量边界为[-1,1],适应度函数z同公式(11)。

2.7.4 麻雀算法 麻雀搜索算法(Sparrow search algorithm,SSA)是一种模拟麻雀在自然界中觅食行为和反捕食行为得到最优种群值的优化算法。根据麻雀在自然界中的捕食行为,将种群个体划分为3类。发现者负责搜索具有丰富食物的区域,为加入者提供觅食方向;警戒者在发现捕食者时发出报警信号[21]。SSA算法的相关参数设置为:最大迭代次数为30,种群数为10,粒子边界为[-1,1],发现者总人口占比20%,适应度函数z同公式(11)。

2.8 BP神经网络仿真实验

2.8.1 训练结果分析 BP神经网络的训练拟合精度达到92.88%,标准PSO-BP网络的拟合精度达到97.60%,GA-BP网络的拟合精度达到94.45%,SSA-BP网络的拟合精度达到96.19%,而改进的PSO-BP网络的拟合精度达到98.31%,具体见图1。根据拟合精度来看,改进的PSO-BP网络训练拟合精度逼近能力最强,适应性更好。

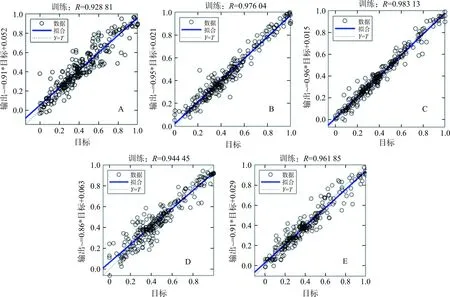
A.BP神经网络;B.标准PSO-BP神经网络;C.改进的PSO-BP神经网络;D.标准GA-BP神经网络;E.改进的SSA-BP神经网络

图2表明改进后的粒子群算法能够有效地优化BP神经网络,网络的收敛速度明显加快,可以明显地看出粒子多次跳出最优值进行搜索,避免了陷入局部最优。当进化代数为14代时,适应度已达到最优。

图2 改进的PSO-BPNN与标准PSO-BPNN的适应度曲线

2.8.2 预测结果分析 对颜色预测的5种模型结果进行了对比,改进的PSO-BP网络模型的平均绝对百分比误差为0.411 5,均方根误差仅为2.164 6,见表4。结果表明,改进后的PSO-BP网络模型的鲁棒性和预测能力更突出,获得了更小的均方根误差和平均绝对百分比误差。改进后的PSO-BP网络模型的平均色差和色差波动范围更小,结果更优,具体见图3。在本研究中改进的PSO-BP模型能够最好地预测色素质量分数与色差值的规律(图4)。

A.BP神经网络;B.标准PSO-BP神经网络;C.改进的PSO-BP神经网络;D.标准GA-BP神经网络;E.改进的SSA-BP神经网络

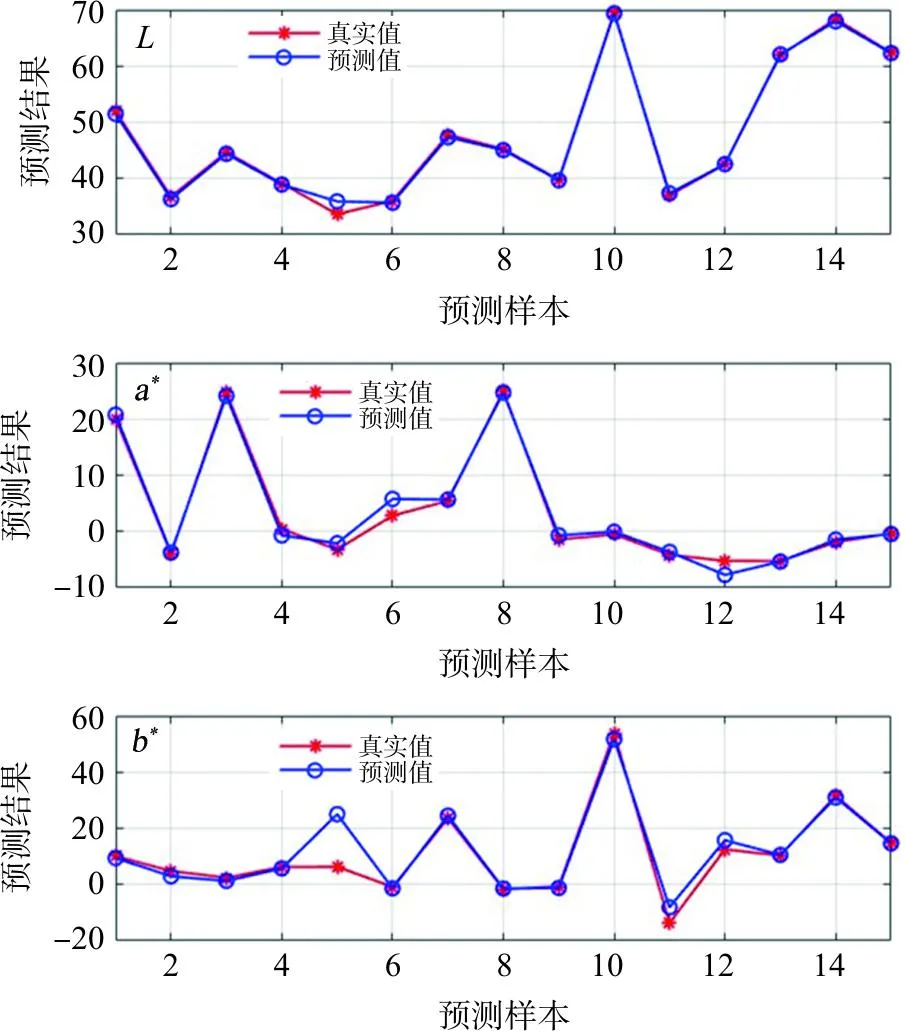
图4 基于改进的PSO-BP模型的L、a*、b*值预测结果对比

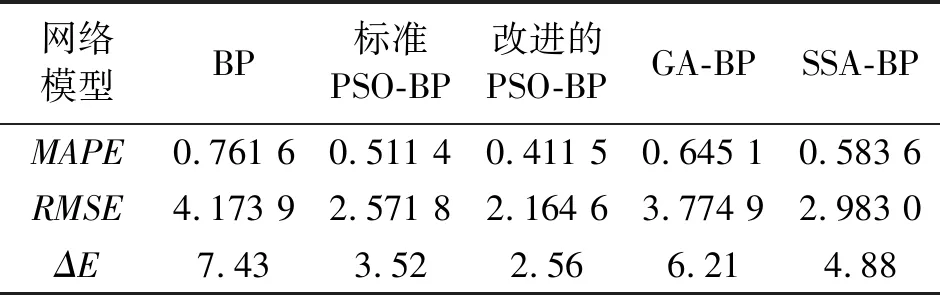
表4 3种网络模型预测结果

2.9 BP神经网络模型验证

对训练好的模型进行准确性测试,选取3种颗粒剂样品,由模型进行配色方案的预测,预测结果见表5。根据预测出的着色剂质量分数,按照“2.1”项下样品的制备方法制备安慰剂样品,进行验证试验,具体结果见表6。将样品与制备好的安慰剂样品放置在一起,肉眼观察比较,结果见图5。实验测试中2组配色满足人视觉感知,而剩余一组不满足,但结果相差不是很大,可以通过稍微修正配色数据完成配色。结果表明基于改进的PSO-BP网络模型具有较高的配色准确性,可以应用于实际生产中。

表5 着色剂用量预测结果

表6 配色准确性测试结果

注:A.芪葛颗粒模型药物;B.芪葛颗粒安慰剂;C.小柴胡颗粒模型药物;D.小柴胡颗粒安慰剂;E.运脾化痰通窍颗粒模型药物;F:运脾化痰通窍颗粒安慰剂

图5 模型药物与所制备安慰剂的直观图

Fig.5 Visual diagrams of model drugs and its placebos

3 讨论

本研究使用色差仪测量颗粒颜色L、a*、b*值,经前期绘图表明该模型颜色参数与质量分数之间为非线性关系,基于神经网络非线性的特点,选择建立神经网络模型预测色素配方。单一的神经网络模型一方面会因为迭代次数难以确定,导致迭代次数过多出现过拟合,或者迭代次数太少导致误差过大;另一方面在迭代寻优过程中容易陷入局部最优,无法达到全局最优[22],因此引入不同优化算法增强传统神经网络的学习能力和泛化能力。不同算法的寻优过程的侧重点不同,导致模型预测误差发生变化,结果表明,改进的粒子群算法更适合安慰剂制备着色剂用量预测模型,在克服神经网络连接权值与连接阈值无法达到全局最优的问题方面,改进的粒子群算法能更好地解决神经网络的缺陷,建立具有较强可靠性的安慰剂制备着色剂用量预测模型。

本研究建立中药复方颗粒安慰剂颜色、安慰剂着色剂配方之间的神经网络模型,相比之前依靠人工经验摸索制剂处方,神经网络模型可以更加快速、便捷、准确地模拟中药安慰剂颜色,一定程度上解决了中药安慰剂由于其独特色泽而难以模拟以及模拟过程中随机性、盲目性大的难题,为中药复方制剂安慰剂制备中颜色的模拟提供了新思路。但该方法仍需进一步地完善,例如在中药安慰剂颜色模拟过程中,不仅仅是颗粒颜色的模拟,还存在溶化后溶液颜色的模拟,但是颗粒颜色和溶液颜色是相互影响的,想要同时模拟两者的颜色还需要更加深入的研究。