一种高效轻量的双参数椭圆曲线数字签名批量验证方案①

巫光福, 傅晓艳, 周建东

(江西理工大学信息工程学院,江西 赣州 341000)

0 引 言

数字签名算法(DSA)利用非对称加密技术实现信息身份认证、数据完整性验证和防篡改[1]。在区块链中,每个交易需要经过数字签名验证才能添加到区块中。然而,大规模交易任务的签名验证会给节点带来繁琐的开销,降低了验证效率[2]。因此,如何提升签名验证的效率成为关键问题。目前,椭圆曲线数字签名算法(ECDSA)仍是区块链领域中的主流算法之一[3]。然而,该算法的实现过程中存在两个主要的数学问题:一是模逆运算,其耗时是乘法运算的十倍[4],二是标量乘运算[5],在签名和验证阶段都要进行,因此它们是影响ECDSA效率的重要因素。针对这两个问题,各种改进ECDSA模逆运算和标量乘运算的方案相继被提出[6-9]。Liu等人[9]提出一种针对区块链的双参数ECDSA,能有效提升签名验证的效率。然而,这些方案都是基于独立验证方式进行的,面对大量的签名验证任务,使用独立验证方案还不足以达到时间要求。1994年,Fiat[10]提出了批量验证的概念,该方法能同时验证多个签名,减少重复计算操作,大大节省了验证器的计算资源和验证延迟。在DSA、RSA等签名方案中,批量验证已经被广泛应用[11-12]。针对ECDSA,研究学者们提出了各种批量验证方案。例如,Xiong等人[2]和Karati等人[13]分别提出了ECDSA批量验证方案。尽管现有的技术试图减少验证时间开销,但对于较大规模的签名验证,大多数批量验证方案的验证效率并不高[14]。为了提升大规模验证任务的效率,我们提出一种高效轻量级的双参数ECDSA批量验证方案。TP-ECDSA在无模逆运算的基础上引入批量验证,能一次同时验证多个签名,并引入KGLP算法加速标量乘运算[15],极大地缩短了验证时间,提升算法效率。实验数据表明,在验证相同规模的消息签名时,使用批量验证和KGLP算法能极大地缩短运行时间开销,验证效率显著提升。

1 基础知识

1.1 椭圆曲线

椭圆曲线(ECC)是定义在有限域上的一种代数结构,通常用于加密和数字签名等密码学领域。设E为椭圆曲线,Fp表示素数域(p是大素数),该椭圆曲线可以表示为:

E(Fp):y2=x3+ax+b(modp)

(1)

其中a,b∈Fp且为常数,对于任意的(x,y)∈E(Fp)。

1.2 椭圆曲线数字签名算法

椭圆曲线数字签名算法(ECDSA)是一种基于椭圆曲线的数字签名算法,其可用于验证消息的完整性和不可否认性等。ECDSA密钥(d,Q)对由满足Q=dP的公钥Q和私钥d组成,其中P是E(Ep)上阶为n的基点。

签名阶段:签名者生成消息m的ECDSA签名(m,r,s),其主要步骤如下:

1)签名者随机选取一个临时密钥k∈[1,n-1],计算R=kP;

2)计算r=x(R)(modn),其中x(R)是R的x坐标。若r=0,则返回1);

3)计算s=k-1(H(m)+dr)(modn),H(m)是哈希函数。若s=0,则返回1);

4)签名者生成消息m的签名(m,r,s)并发送给验证者。

验证阶段:验证者收到签名者的签名(m,r,s)后,进行如下验证:

1)验证者先检验r,s∈[1,n-1]是否成立,若否则验证不通过;

2)计算e=H(m),接着计算v=es-1(modn),u=rs-1(modn);

3)计算R=vP+uQ,r′=x(R)(modn);

4)验证者验证r′=r是否成立,若成立则接受该签名,否则拒绝。

在ECDSA算法中,签名和验证阶段各需一次模逆运算。若数据规模为N,一次模乘运算的复杂度为O(N2lnN),而模逆运算的复杂度为O(N3),比模乘运算高一个数量级。因此,在该算法中应尽量避免模逆运算,以提高签名验证效率。

1.3 批量验证

批量验证是一种能同时验证多个签名的技术,适用于ECDSA。在区块链系统的大规模交易中,需要验证消息签名有很多,若一个一个地进行验证,将会耗费大量的时间和计算资源。批量验证技术可以同时验证多个消息签名,能有效提高签名的验证效率,同时也能够降低验证的计算成本。

验证多个或单个签名者生成的ECDSA签名的标准方法如所示。

在多个签名者的情况下验证t个签名对,

(2)

在同一签名者的情况下验证t个签名对,其公钥相同,有Q1=Q2=…=Qt=Q,

(3)

ECDSA批量验证方案可以将验证阶段的标量乘运算量从2t减少到[2,t+1],极大缩短了签名验证的时间开销。

2 双参数椭圆曲线数字签名批量验证方案

2.1 双参数椭圆曲线数字签名算法

传统的ECDSA方案在签名阶段和验证阶段均存在耗时的模逆运算,其运算时间开销是点乘运算的十倍。为了提升ECDSA方案的效率,提出了TP-ECDSA方案,该方案在保证效率的前提下,引入了两个随机参数,且使用汉明权重替代消息的哈希值,避免了模逆运算。TP-ECDSA方案在保证安全性的前提下大大提升了运算效率。具体方案如下:

签名阶段:签名者生成消息m的TP-ECDSA签名(m,r,s,β),其主要步骤如下:

1)签名者随机选取一个临时密钥k∈[1,n-1],计算R=kP;

2)计算r=x(R)(modn),其中x(R)是R的x坐标。若r=0,则返回1);

3)签名者再随机选择两个整数α,β∈[1,n-1],且满足k=αr+βm;

4)计算e=H(m)和其汉明权重w;

5)计算s=αr+(w+r)d(modn)。若s=0,则返回1);

6)签名者生成消息m的签名(m,r,s,β)并发送给验证者。

验证阶段:任何验证者都可以通过以下步骤检验签名(m,r,s,β)是否有效:

1)验证者先检验r,s,β∈[1,n-1]是否成立,若否则验证不通过;

2)计算e=H(m)和其汉明权重w;

3)计算v=(s+βm)(modn)和u=(w+r)(modn);

4)计算R=vP-uQ和r′=x(R)(modn);

5)验证者验证r′=r是否成立,若成立则接受该签名,否则拒绝。

2.2 TP-ECDSA批量验证方案

现有的ECDSA批量验证方案对相同或不同签名者的多个签名都是有效的。虽然现有的一些ECDSA批量验证方案是安全高效的,但随着批量规模的增大,验证效率有所降低。在区块链中,大规模交易任务的批处理量相对较高,现有方案将不适用。方案以少量的模乘和标量乘运算为代价,对各种规模的消息签名验证都有较好的性能。对于该方案,在无模逆运算的基础上主要耗时的是标量乘运算,使用批量验证能减少标量乘运算,有效降低签名验证时间开销。

2.2.1 相同签名者的TP-ECDSA批量验证方案

相同签名者的密钥对(d,Q)一致,在验证t个签名对(mi,ri,si,βi)时,根据TP-ECDSA方案的验证算法,需要2t次标量乘运算,而该方案只需2次标量乘运算,能极大地提高签名的验证效率。相同签名者的TP-ECDSA批量验证方案如算法1:

算法1：相同签名者的TP-ECDSA批量验证方案

输入:t个消息签名对(mi,ri,si,βi)和密钥对(d,Q);

输出:接受或拒绝一批签名;

1.验证者先检验ri,si,βi∈[1,n-1]是否成立,若否则拒绝这批签名;

2.计算ei=H(mi)和汉明权重wi;

3.计算vi=(si+βimi)(modn)和ui=(wi+ri)(modn);

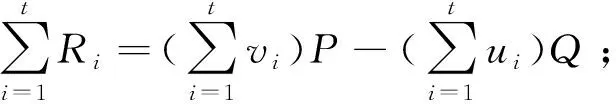
5.判断第4步中的等式是否成立,成立则接受这一批签名,否则拒绝。

2.2.2 不同签名者的TP-ECDSA批量验证方案

不同签名者的密钥对不同,假设有t个签名者,其密钥对为(di,Qi)(i=1,2,…,t)。针对不同的消息m,产生t个签名(mi,ri,si,βi)(i=1,2,…,t),使用TP-ECDSA在验证阶段需要2t次标量乘运算,而该方案仅需t+1次,签名验证效率大大提升。不同签名者的TP-ECDSA批量验证方案如算法2:

算法2：不同签名者的TP-ECDSA批量验证方案

输入:t个消息签名(mi,ri,si,βi)和密钥对(di,Qi);

输出:接受或拒绝一批签名;

1.验证者先检验ri,si,βi∈[1,n-1]是否成立,若否则拒绝这批签名;

2.计算ei=H(mi)和汉明权重wi;

3.计算vi=(si+βimi)(modn)和ui=(wi+ri)(modn);

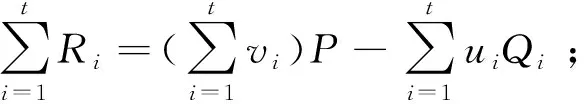
5.判断第4步中的等式是否成立,成立则接受这一批签名,否则拒绝。

方案是基于TP-EDCSA实现的,在无模逆运算的基础上进一步降低标量乘计算的时间开销。在验证过程中,随着签名对数量的增加,其验证所花费时间相对减少。因此,对消息签名进行批量验证将进一步减少验证时间,使得验证方案在实际应用中更加高效。

2.3 KGLP算法

在ECDSA批量验证方案中,最耗时的运算是标量乘运算和模逆运算。TP-ECDSA批量验证方案中无需模逆运算,故该方案中最为耗时的是标量乘运算,因此对该运算进行优化能加速验证效率。使用KGLP算法加速标量乘运算,该算法能同时计算多个点的标量乘,减少加倍运算的次数,提高计算效率。

算法3KGLP加速验证算法

输入:vi=(vi,l,vi,l-1,…,vi,1),Qi∈E(Fp),i∈[1,l]

1.QQj=jt-1Qt-1+…+j0Q0,

j=(jt-1,…,j0)2,j∈[0,2t-1],; \任意组合t点标量相加的预计算结果

2.T←∞;

3.fori=t-1;i≥0;i--do

4.T←2T;

5. Forj=t-1;j≥0;i-- do

6.bit=vj,i≪j;

7.T=T+QQbit;

8.returnT.

2.4 正确性验证

对不同签名者的TP-ECDSA批量验证方案进行正确性验证。若有t个签名者生成t个签名(mi,ri,si,βi)(I=1,2,…,t),与批量验证相关的公式有:Qi=diP,Ri=kiP,ei=H(mi),wi,si=αiri+(wi+ri)di,则可证明有:

由此可以证明提出的方案是正确的。对相同签名者TP-ECDSA批量验证方案的正确性证明与之相似,略。

3 性能分析

为了验证TP-ECDSA批量验证方案的性能,比较了传统ECDSA与TP-ECDSA的独立验证和批量验证。基于电脑端的实验运行环境为:

版本:Windows 11,64位操作系统,基于x64的处理器;

中央处理器(CPU):Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz;

内存:8.00 GB;

使用C语言实现本文各种方案,调用OpenSSL开发包源代码中安全曲线的参数(OpenSLL库是一个开源密码库,提供大量的加密算法和密钥协议),在Visual Studio2021中进行编程。在OpenSSL开发包开源程序的基础上,分别使用spec256k1实现大素数域ECDSA与TP-ECDSA的独立验证和批量验证。

使用ECDSA与TP-ECDSA实现相同签名者和不同签名者的独立验证和批量验证,将每个方案运行100次,取其数据平均值。相同签名者和不同签名者的签名验证方案在密钥生成阶段的耗时不同。因为相同签名者方案只需生成一组密钥对,而不同签名者方案需要生成多组密钥对。而在签名验证过程中,它们各部分所需的时间几乎相同。在不同规模的消息签名数量下,表1给出了相同签名者进行独立验证和批量验证的运行时间开销,表2给出了不同签名者进行独立验证和批量验证的运行时间开销。从表 1中可以看出,在对16个消息签名进行验证时,ECDSA的独立验证耗时4737 ms,批量验证耗时408 ms,而TP-EDCSA的独立验证耗时38 ms,批量验证仅耗时4.8 ms。从中可以看出,相对于独立验证,批量验证能够减少时间开销,特别是文中提出的TP-ECDSA批量验证方案的签名验证耗时更低。

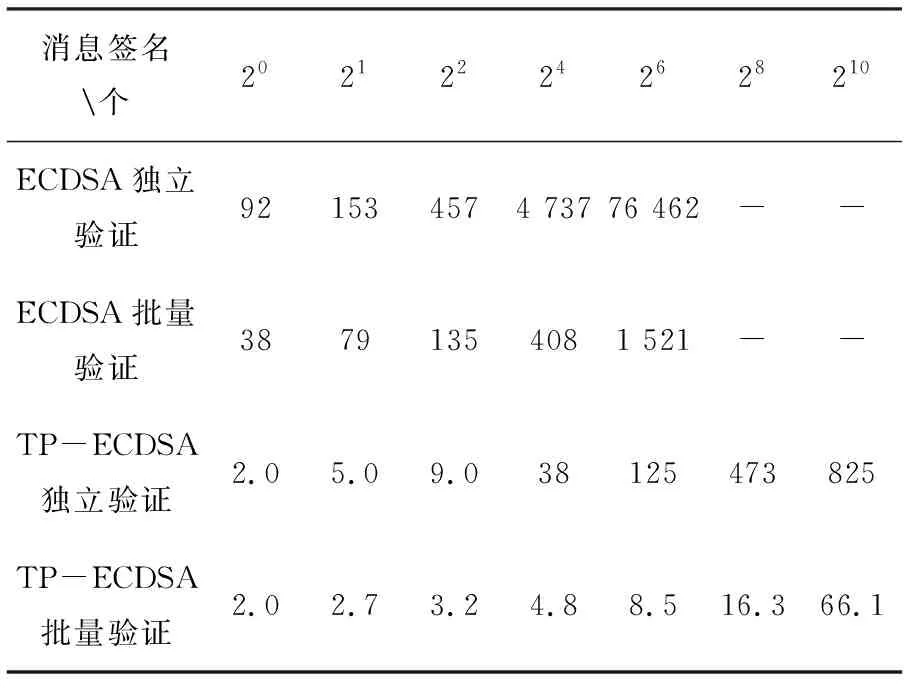
表1 不同签名者在独立验证和批量验证下的时间开销(ms)

表 2 相同签名者在独立验证和批量验证下的时间开销(ms)

图1 有无使用KGLP算法的TP-ECDSA批量验证方案时间开销对比

在图 1中,展示了TP-ECDSA批量验证方案是否使用KGLP加速验证算法的时间开销,可以看出使用KGLP算法的批量验证方案的验证性能更优。图 1中的横坐标2x(x=0,2…,10)表示签名数量。从图中可以看出,随着签名数量规模的增大,使用KGLP算法的方案在时间开销上增长速度较为平缓,而未使用KGLP算法的方案在时间开销上增长速度较快。当签名数量为1024时,未使用KGLP算法的TP-ECDSA批量验证大约需要69 ms,而使用KGLP算法的仅需12.7 ms,运行速度优化了81.6%。因此,对于大规模消息签名进行同时验证时,引入KGLP算法的TP-ECDSA批量验证能极大降低验证时间,显著提升效率。

4 结 语

为了提升区块链中大规模消息签名的验证效率,在TP-ECDSA无模逆运算的基础上,提出一种高效轻量的双参数椭圆曲线数字签名批量验证方案。方案可以一次验证相同签名者或不同签名者的多个签名,极大地减少了验证时间。与独立验证相比,TP-ECDSA批量验证方案计算标量乘的次数更少,且利用KGLP算法能加速耗时的标量乘运算,从而大大提升验证速度。实验分析表明,我们的方案是一个优秀的方案,因为它比现有的批量验证方案具有更高的计算效率。相信未来该方案可以应用于区块链系统中的数字货币交易。