基于原位测量的交直流复合电压对金属化膜自愈特性影响的研究

吴致远，王卓容，刘靖舟，刘尚书，仝殿杰，齐红斌，王建涛，党智敏，王伟，屠幼萍

（1.华北电力大学高电压与电磁兼容重点实验室，北京 102206；2.清华大学电机系，北京 100084）

0 引言

近年来我国大力发展特高压直流输电，在交直变电过程中需要大量换流阀[1]，其中干式直流电容器是换流阀的核心组件，现今聚丙烯金属化膜为其常用介质材料，相较于箔式电容器[2]，金属化膜电容器由于其具有特殊的“自愈”特性，在投入使用前可通过“赋能”工艺去除电弱点，使其工作电压更高，储能密度更大，目前美国聚丙烯金属化膜电容器储能密度达到3 kJ/L[3]。

现在国内对于介质材料研究较多，通过复合介质、梯度材料，表面改性工程等方法可以大大提高聚丙烯的储能密度和击穿场强。但是对于其后续工艺金属化及其自愈特性的研究较少，华中科技大学李化[4]等人搭建金属化膜自愈测试平台，对自愈特性进行温度、压强、电压的分析测试，温度达到80 ℃，压强在1 MPa 以下，谐波为100 V 有效值；孔中华[5]等人通过对不同单一物理场变化对自愈特性进行实验验证总结出宏观自愈特性的影响规律；以上学者都研究了单一因素对自愈特性的影响，未考虑多应力共同作用下自愈特性的演变规律。但作为需要实际运行在电网下的器件，其必定是承受多应力的共同作用，且由于在电网运行下必然存在谐波，直流电容器并不止承受直流，还有谐波成分[6]。所以，在复杂应力下交直流电压对自愈特性演变规律的研究就变得尤为重要，但是现今缺少微米级超薄膜自愈特性的原位测试平台和测试数据[7]，我国干式直流电容器产业链上亟需此类原位测量数据来检验其器件可靠性。

本文搭建了微米级薄膜自愈特性测试平台，可实现复杂应力下自愈特性的原位测量，实现了电、热、力3 种应力的自由叠加。自愈实验以换流阀中电容器实际运行条件为基准，3 种应力共同施加，研究多应力下交直流对自愈特性的影响规律，同时提出自愈热力学理论模型，并进行实验验证。

1 自愈特性原位测试平台

测试平台主要有3 种应力施加，电场、温度场、机械应力3 种。

1.1 电场

由于存在交直流叠加，为使得高额交流分量能大量通过试样，而不会从稳压电容中流走，本实验电路设计增加了谐振分路，uc0(t)和ic0(t)分别是实验测得的自愈电压和自愈电流，id(t)是自愈发生时稳压电容提供的电流。实验平台电路拓扑图见图1。

图1 实验平台电路拓扑图Fig.1 Circuit topology of experimental platform

1.2 温度和机械应力

温度的施加主要是通过油浴加热板贴合薄膜试样，基于热传导来实现，工字夹具向薄膜施压及自制绝缘夹具往两侧拉伸来模拟层间压强和卷绕张力。实验平台温度和机械力场图见图2。原位自愈特性测试平台实物图见图3。

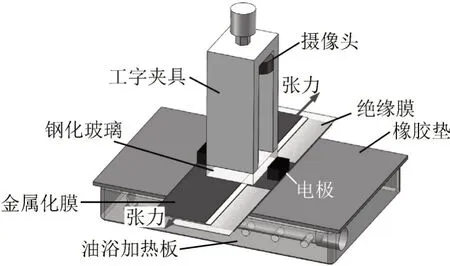
图2 实验平台温度和机械力场Fig.2 Temperature and mechanical force field of experimental platform

图3 实验平台实物图Fig.3 Physical diagram of experimental platform

1.3 原位自愈特性测试实验方法

3 种应力施加顺序为卷绕张力-温度-层间压力-电场。将薄膜如图3 摆放方式在平台上摆放好，用夹具夹住所有试品双向拉伸，达到指定张力后固定夹具。随后开启油浴循环器，加热15 min后，用热电偶测量下层薄膜上表面和玻璃板上表面温度，当温差小于1℃时，认为温度已稳定。控制万能拉力机横梁，通过工字夹具向薄膜施加指定压强，最后通过信号发生器配合功率放大器施加交直流复合电压。

2 实验结果分析和自愈模型

为了更符合换流阀中支撑电容器的实际运行情况，测量的数据更符合原位自愈特性，电压参数设定参考了中国长江三峡公司的仿真数据[8]，实验将直流DC 设为2.8 kV，交流分量采用1st、2nd、3rd3 种谐波等比共同混合的方式，分别为100：15：1，即直流不变，3 种交流分量各自占交流总量的比例不变，改变总交流量占直流的比例，本实验设定总交流量占直流比例为1%、5%、10%、15%、20%5 种。实验选取自愈点为交直流混合电压值峰值附近的自愈点，对照实验组选取相同电压值下纯直流自愈点，DCmix+ACmix=DC，在相同电压等级下进行表征对比。

2.1 交直流和层间压强的影响

面积、能量和交直流种类的关系见图4。从图4 实验结果中可以看到在0.1 MPa 的低压强下，自愈能量和面积都随着电压的升高而升高，能量分布于2~10 mJ，面积分布于2~10 mm2。当电压的值相同时，相比于交直流混合，纯直流下的自愈能量略微高于交直流复合，且随着交流含量的升高而升高。

图4 面积、能量和交直流种类的关系Fig.4 Relationship among area，energy and AC-DC class

但是拟合曲线在数值上相差的最高值为5%，且由于自愈能量与面积存在强线性关系，自愈面积的值同样反映出在相同的电压值下，纯直流比交直流混合面积略大的特性，在交流含量最高的20%时，拟合曲线差值达到10%。这可以用界面电子注入的理论来解释[9]，由于金属化膜存在纳米级金属层和有机聚合物介质的界面，交直流混合电压对界面电子存在抽出和注入的现象，这会对材料的本征结构造成破坏[10]，致使交直流环境下材料出现了“劣化”特性[11]，尤其是到了20%的交流值的情况下，这种“劣化”特性更加明显，导致自愈能量和面积的下降。

到了10 MPa 的高压强下，自愈能量和面积大幅减小，交直流影响几乎不体现，同电压值下交直流混合和纯直流在拟合曲线上几乎没有区别，这说明机械压强的施加减弱了电压的影响，自愈的演变规律出现了变化。

0.1 MPa 下面积和能量关系见图5-6。当压强为0.1 MPa 时，面积和能量呈正相关见图5，且从拟合曲线上看，不论直流还是交直流混合，面积与能量都有很强的线性关系这从以往的文献也能看出，李化团队[12]的研究成果证明S∝Wsh，这和本文在低压强下的的研究结果相同。

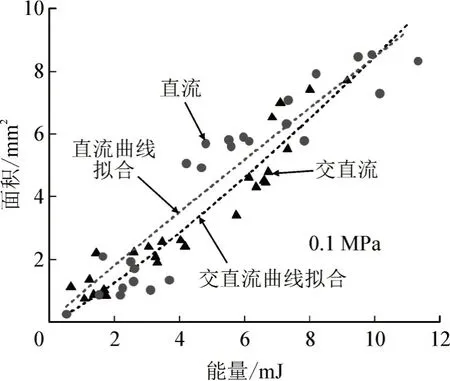
图5 0.1 MPa下面积和能量关系Fig.5 Relationship between area and energy at 0.1 MPa

图6 10 MPa下面积和能量关系Fig.6 Relationship bewteen area and energy at 10 MPa

将能量和面积联系起来，可以看出不论在0.1 MPa 的低压强下还是10 MPa 的高压强下，自愈能量和面积始终呈现非常强的线性关系，这说明自愈能量决定了自愈面积的大小，而自愈面积又决定着金属化膜电容器的电容大小，决定着器件的使用寿命[13]，因此，对于电容器使用寿命的研究，应着重于自愈能量的构成和自愈行为的动态行为模式。

2.2 自愈热力学模型

建立金属化膜自愈特性的热力学模型需要先明确自愈行为的能量来源[14]，自愈的产生是由击穿引发的电弧电流的焦耳热所决定的，故以金属层为建模对象[15]，建立热通量模型，以反应在微秒级动作下的演变过程，模型结构示意图见图7。

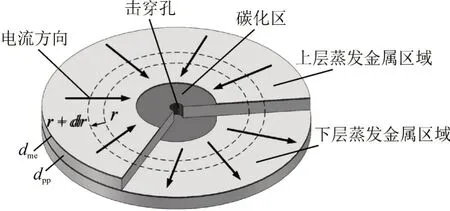
图7 自愈热力学模型Fig.7 Thermodynamic model of self-healing

dme和dpp分别是金属层厚度和聚丙烯厚度，当电流流过时会有趋肤效应，趋肤深度公式为

本模型以常用金属材料铝为模型参数，为金属层铝的电导率，τ为自愈持续时间，μ为铝的磁导率，当τ取1 μs 时，电流的趋肤深度可达10 μm，远远超过金属层的厚度（10nm），所以在金属层中电流密度是一个关于仅关于半径r的函数，即在同一半径下电流是均匀的。金属层辐射散热公式为

式中：er为金属铝的发射率；T0为初始温度；T为材料所处温度；σSB为玻尔兹曼常数，热辐射散热能量Qr远小于自愈能量WSH，故忽略不计，所以自愈热力学模型公式为

式中：kPP为聚丙烯传热系数；h为对外界散热系数；dme为金属层厚度；ρAl为金属铝密度；Cp为金属铝热容；r为积分假设圆环半径；I(t)为自愈电流。

金属层传导传热半径公式为

式（4）是一个关于时间τ的函数，τ在本文中定义为自愈持续时间，铝的导热系数kme=8.61×10-5m2∙s-1，自愈持续时间τ约为10 μs，计算出传热半径约为100 μm，这个传热半径相较于自愈半径（mm 级别）而言可略去，故自愈热力学模型中金属层的热传导忽略不计，聚丙烯介质的热传导由于聚丙烯的导热系数为kpp=1.2×10-7m2∙s-1，远远小于金属层的传热速度，故聚丙烯的热传导忽略不计。

金属层对外界泄漏散热，这是热力学模型的第二项[16]，此项对外散热为自愈现象结束后对外界的热量流失，h为空气散热系数约为100 J∙(sm2k)-1，dme约为100 nm，ρAlCp约为2.38×106J∙(sm2k)-1，但是作用时长时间需要约为200 μs，远远长于自愈持续时间（数十微秒），故忽略不记。以上对模型的修改，最终将自愈热力学模型简化为只有焦耳热的产生和消耗，公式为

模型计算如下，可得

式中：和为固态铝密度和热容，Tm为铝熔点，第一阶段由于需要考虑金属从固态到液态的相变潜热，故提出等效液化温度Lm是金属从固态到液态相变潜热，T0是初始温度，tm是金属层由固态转化为液态的时间，是一个固态铝电导率，是一个关于温度的函数，表达式为

式中：α是系数，其值为5×10-3K-1，为简化计算将电阻率定为T0至Tm的均值记为。

第二阶段为金属从液态到气态的过程，公式为

式中：和为液态铝密度和热容；tm为液化铝的时间；Tv为液态铝的气化温度，由于有金属相变，必然存在有潜热，因此等效的气化温度为，=Tm+Lv/，Lv是金属从液态到气态的潜热，同理，液态金属铝的电导率公式为

为简化计算，液态下金属铝的电导率取Tm至Tv的均值，记为。

将等式进行变换如下：

自愈面积SSH表达式为

由最终表达式可知SSH最终是关于dt的一个正相关函数，模型所有参数取值罗列见表1。

表1 模型参数Table 1 Model parameter

将参数代入模型计算，并选取两种层间压强对应实验数值进行比对，见图8-9。

图8 0.1 MPa下实验与模型计算Fig.8 Experimental and model calculation at 0.1 MPa

图9 10 MPa下实验与模型计算Fig.9 Experimental and model calculation at 10 MPa

通过上图结果可知，本文建立的自愈热力学模型在低压强下与实验结果相吻合，基本服从线性正比关系，印证了模型的可靠性，并从自愈热力学行为上证明在低压强下自愈的面积主要由焦耳热决定[18-20]。但是在10 MPa 高压强下，模型仿真结果与实验偏差较大，且模型不符合能量与面积的线性关系，这说明在高压强下自愈面积与焦耳热的关系出现了变化，压强的施加影响了焦耳热[21-26]，并进一步影响到自愈的行为模式，导致自愈面积和能量的关系出现了变化，后续需要考虑高压强下自愈模型的改进。

3 结语

1）在0.1 MPa 压强、相同电压等级下，直流电压下的自愈能量和面积比交直流混合的自愈能量和面积略大，差值随着交流含量的升高而升高。

2）在10 MPa 压强下，由于机械应力的介入，自愈能量和面积大幅减小，且电压种类的影响可忽略不计。

3）不论在0.1 MPa 下还是10 MPa 下，自愈面积和自愈能量存在非常强的线性正相关性。

4）自愈热力学模型在0.1 MPa 下有非常好的仿真结果，但是在10 MPa 高压强下和实验测量数据相差很较大，对于在高压强下的自愈模型仍需要改进。